皮尔逊-Ⅲ型频率曲线可视化程序开发
高国辉,任玉珊,高金花
(长春工程学院,长春130012)
0 前言
频率曲线是获得设计洪水和其他水文要素的外延工具,在水文计算中具有广泛的应用,水文随机变量究竟属于何种概率分布,目前还没有得到充分的论证[1]。我国在进行水文频率计算时,普遍采用的是皮尔逊-Ⅲ型分布,因此确定皮尔逊-Ⅲ型理论频率曲线在水文频率计算中尤为重要。确定该曲线的传统方法为适线法,该方法最终要找出一组参数,使其对应的皮尔逊-Ⅲ型理论频率曲线与实测点距匹配最佳[2]。传统适线法要多次修改参数,且适线时要选用离均系数表进行多元插值,每次改变参数均要绘制理论频率曲线,整个过程十分麻烦。随着计算机技术和数值模拟技术的发展,传统适线法已经不能满足人们对计算速度和精度的要求,笔者运用Microsoft Visual Studio 2008软件平台中的C#语言开发了频率曲线可视化软件,自动实现上述过程,计算速度快,并以多种形式对结果进行储存,方便调用查看,为工程设计节省了大量的人力物力,缩短工程设计周期,同时该软件可视化程度高,具有一定的教学意义。
1 皮尔逊Ⅲ-型函数
皮尔逊型Ⅲ-函数数学上常称伽玛分布,其概率密度函数为:

式中α0,α,β>0为参数。
根据概率论可求得其数学期望和方差分别为:

同时还可以证明其CV,CS分别为:

因此,3个原始参数α0,α,β可以用基本参数E(X),CV,CS表示如下:

水文计算中,一般需要求出指定频率p所相应的随机变量xp的取值,也就是通过对密度曲线进行积分,即:

用代换积分法,令t=-β(x-α0),得:

式中tp=β(xp-α0)。当p已知时,tp仅依赖于α和CS,可以推导出[1]:

整理得标准化的形式:
2.用量及方式。肥水时水位要深。建议平台水位30cm以上,沟中80cm以上。从12月开始至第二年2月每月施一次腐熟的有机肥,每次每亩用量在100kg左右,具体视水质情况酌情增减。全池泼洒或将腐熟粪肥用蛇皮袋装好后,浸泡在水中,每隔一段距离放置一袋。
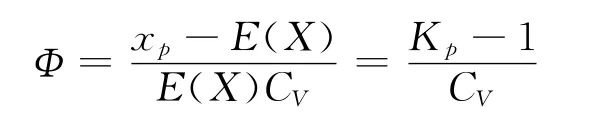
式中Kp为xp的模比系数,且定义Φ为离均系数。
若tp已知,则xp可从下式求得:
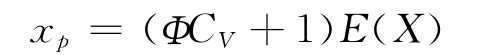
因此,在已知x、CV及CS的条件下,即可画出理论频率曲线,可以通过皮尔逊型—Ⅲ型分布离均系数Φ值表查得相应CV和CS下的Φ值。
2 适线法基本原理
将x1,…,xn由大到小排队:
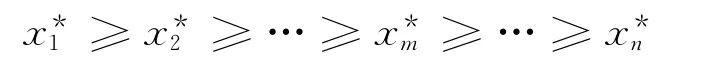
按照下式计算经验(累积)频率Pm=

将(Pm,x)点绘在特定的坐标纸上(一般是正态概率格纸),由于样本来自总体,因此,只要n足够大,这些点就分布于X的分布函数曲线附近,据此,选取一组参数u1,…,ul,代入函数P=G(x;u1,…,ul),从而可以在坐标纸上画出(P,x)曲线,这条曲线叫做理论频率曲线,观察该曲线与经验点距的拟合程度,如拟合程度不高,重新选择参数,重复以上步骤,直至符合要求为止,则最后一组参数即为X分布函数中参数的估计值[3]。
水文上常用的特定坐标纸是正态概率格纸(又称海森机率格纸),正态分布函数在该格纸上为一条直线。
3 程序流程图
本程序是应用Microsoft Visual Studio 2008软件平台中的C#语言开发而成,程序主流程图及运行图如图1~2所示。
程序运行说明:
(1)将初始数据输入文本文档(数据.txt),并将其放在程序目录下。
(2)运行程序,根据程序提示,进行数据的录入、参数计算,图像绘制等。
(3)判断曲线与实测点距是否匹配,如果不匹配则调整参数重复步骤2直至曲线与实测点距匹配完好(整个过程中可以清晰地看到绘图区的曲线和计算结果随着参数变化的变化趋势,实现动态化,方便进行教学演示),然后将计算结果进行保存,结果将以文本文档(结果.txt)和图形(频率曲线.Tiff)2种格式进行存储,方便进行查看调用,同时也便于设计者编写报告。
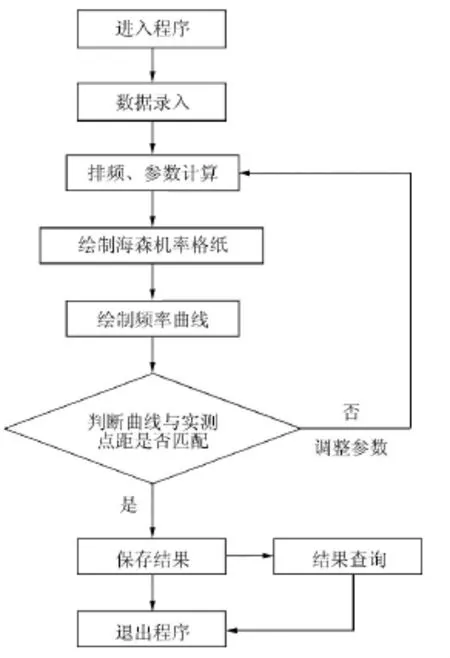
图1 流程图
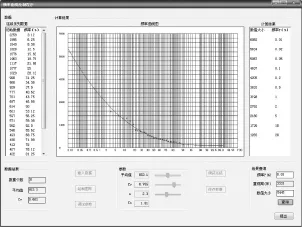
图2 程序界面
(4)程序运行至第(3)步,结果中已显示的数据是常用频率下对应的数据,但有些特殊工程可能需要特殊的数据,为了方便设计者对结果进行双向查询,增加了结果查询功能,设计者可以根据计算结果查询任意频率下的数据结果,同样也可以根据数据的大小查询其对应的频率。
(5)如果没有实测资料,只有设计参数,也可将设计参数输入程序中,实现上述(3)、(4)两部分功能。
4 程序应用
选取某水文站年最大流量资料(见表1)进行程序应用演示。

表1 某水文站年最大流量资料(1956年—1986年)
首先将以上数据依次录入文本文件(数据.txt),存放在主程序目录下,然后运行程序,根据程序提示依次进行计算,调试,最后将计算结果保存在文本文件中(结果.txt),将频率曲线图形保存为图片格式(频率曲线.Tiff),方便进行查看调用。部分计算结果见表2所示。
以上整个过程在几min之内即可完成,相比于传统适线法,极大地提高了工作效率,由此可见,通过该程序可以迅速地计算出相应频率下的流量值,达到事半功倍的效果。
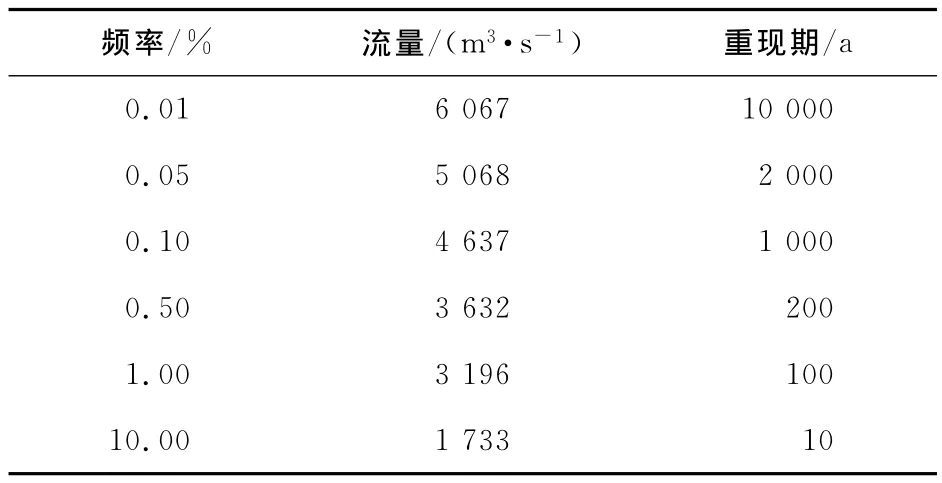
表2 某水文站年最大流量频率计算结果表
5 结语
本皮尔逊-Ⅲ型频率曲线可视化程序具有以下特点:
(1)整个过程对离均系数表进行自动查表、插值计算,绘图速度快,精度高。
(2)如果对计算结果不满意,可以根据经验调整参数,使理论频率曲线与实测点距匹配最佳。
(3)计算结果通过多种方式进行保存(文本文档、图片),方便查看调用。
(4)调节参数的过程中可以清晰地看到各个参数对频率曲线的影响程度,具有一定的教学演示作用。
[1]王德智.皮尔逊-Ⅲ型频率曲线图解适线软件开发[J].水利发展与经济,2009(2):1111-1113.
[2]赵晓慎.皮尔逊-Ⅲ型分布曲线最佳配线及自动化绘图[J].人民黄河,2007(4):25-26.
[3]黄振平.水文统计学[M].南京:河海大学出版社,2003:179-182.

