机动目标ISAR自聚焦新方法

黄大荣，张 磊，邢孟道，保 铮

（西安电子科技大学 雷 达信号处理国家重点实验室，陕西 西 安 710071）

逆合成孔径雷达（ISAR）成像技术通常通过平动补偿将运动目标转换为转台目标[1].平动补偿包括包络对齐和自聚焦.由于成像所需转角一般较小，包络的位移一般小于1个距离分辨单元，因此包络对齐比较容易.常用的包络对齐方法如互相关法[2]和最小熵法[3]等，对于机动目标仍然适用[4].相位误差是相对于雷达波长的，当波长为厘米级时，毫米级的散射点径向走动都会产生明显的相位变化.因此，自聚焦技术是ISAR成像处理的关键.在高分辨雷达成像中，研究稳健高精度的自聚焦技术意义重大[5－9].

对于平稳飞行的目标，已有很多自聚焦方法：加权相位估计自聚焦方法[10]对于相位误差的阶数无要求，具有很强的鲁棒性，但巨大的运算量无法应用于实际中.最大似然估计的特征向量分解法[11]估计的方差可以达到克拉美罗界，但是需要对高维度的协方差矩阵特征值分解，运算量较大、实际应用困难较大.相位梯度自聚焦方法[12]（Phase Gradient Autofocus，PGA）运算量适中且鲁棒性较好，实际中应用最为广泛.但是，传统的自聚焦方法都只考虑多普勒线性相位，并没有考虑二次相位对相位误差估计精度的影响.当目标进行机动飞行时，回波的方位向信号产生随时间变化的多普勒二次分量而被调制成线性调频信号，信号相位中不仅含有多普勒线性相位，还包含由机动引入的二次相位，导致传统的自聚焦方法存在估计精度下降的问题.

为了解决上述问题，笔者提出了一种机动目标自聚焦新方法.通过一维方位像圆平移至图像中心消除多普勒线性相位的影响[1]；通过线性搜索获得方位调频率的最优估计，实现多普勒二次相位项的补偿；通过对所有样本信号的相干积累，降低噪声的影响，实现初始相位的估计；通过多次迭代处理来提高相位误差估计精度.仿真和实测数据处理结果表明，笔者提出的方法具有比传统方法更好的聚焦效果和噪声容忍性.

1 信号模型

机动目标成像的几何模型如图1所示.图1中O点表示机动目标等效到三维转台后的参考点.向量R表示雷达视线方向上的单位矢量，向量ω表示目标的转动向量.R和ω构成成像平面OAC.将向量ω在OAC平面内分解为沿OR方向的向量ωR和与OR垂直的向量ωe.由于ωR不改变目标散射中心的径向距离，ωe导致散射中心产生径向移动，即ωe是有效的转动向量.

假设雷达发射线性调频脉冲信号形式为

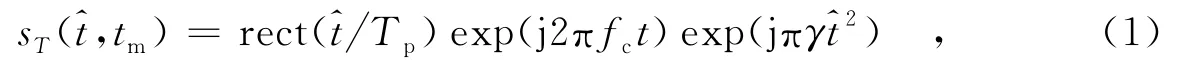
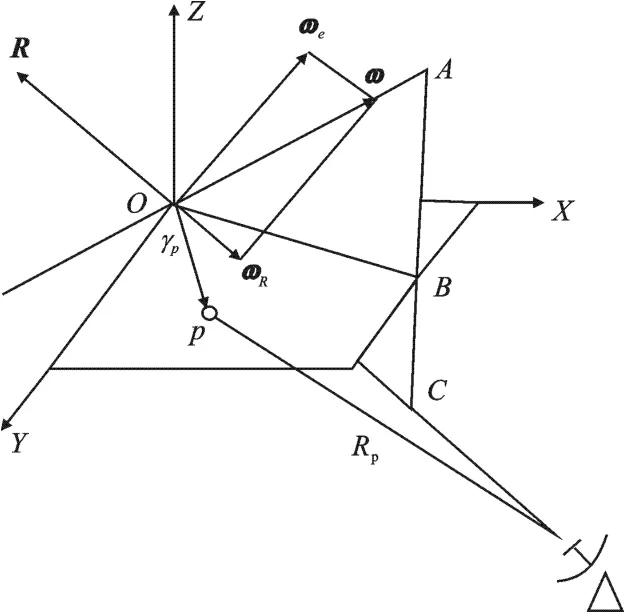
图1 机动目标ISAR成像几何示意图

其中，Tp表示发射信号脉冲宽度，fc表示信号载频，γ表示发射信号的调频率表示距离向快时间，tm表示方位向慢时间，t表示全时间，rect（·）表示发射信号的包络.回波信号经解线频调处理后，对快时间进行傅里叶变换，忽略常数相位项并补偿剩余视频相位（RVP），得到信号差频域的表达式为

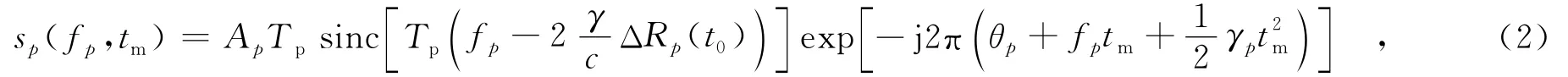
其中，θp、fp和γp分别表示散射点p的起始相位、多普勒相位和方位向调频率.这里假设ωe引起的径向走动仍在一个分辨单元内，即认为回波的包络是非时变的.式（2）是理想情况下的信号模型.实际中机动目标的运动通常是未知的，常会引入严重的运动误差.假设散射点p位于第n个距离单元，经过离散采样后，信号重新表示为

其中，φ（m）表示相位误差，σ（n；m）表示噪声，t表示相邻脉冲之间的时间间隔.此时，相位ψn为

其中，n＝1，2，…，N，m＝1，2，…，M，分别表示距离采样总数和方位总脉冲数；第n个距离单元的初始相位项、多普勒频率项和二次相位项分别表示为

2 机动目标自聚焦

2.1 特显点样本的选择

上述信号模型是建立在距离单元中仅含有1个孤立散射点的假设条件下，实际中理想的孤立散射点几乎不存在，但特显点总是存在的[1].假设信号中共有L个特显点，按强度从大到小排序后，构成样本信号为

2.2 多普勒线性相位补偿

多普勒线性相位通过将信号的一维方位像圆平移至图像中心来消除.可通过对补偿后的信号加窗滤波提高样本的信杂噪比.补偿多普勒线性相位后的信号相位可表示为

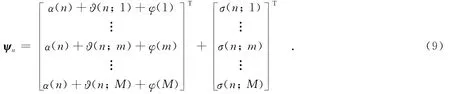
2.3 二次相位补偿

对二次相位项ϑ（n；m）补偿，实际是对方位向调频率γn的估计，可以通过在[γmin，γmax]线性饱和搜索获得.最大峰值处对应γn的最优估计为

其中，⊙表示矢量点乘，FFT[·]表示傅里叶变换，Peak｛·｝表示向量所有元素中的最大值，并有

估计出γn后，与

相乘，信号相位变为

2.4 初始相位的补偿

不同样本信号的初始相位α（n）是不同的，初始相位具有随机性.这里对初始相位的估计提出一种新的方法，通过对所有样本信号的相干积累，避免了相位梯度估计，可获得比PGA更高的相位误差估计精度.首先求出样本信号之间的相位差，即

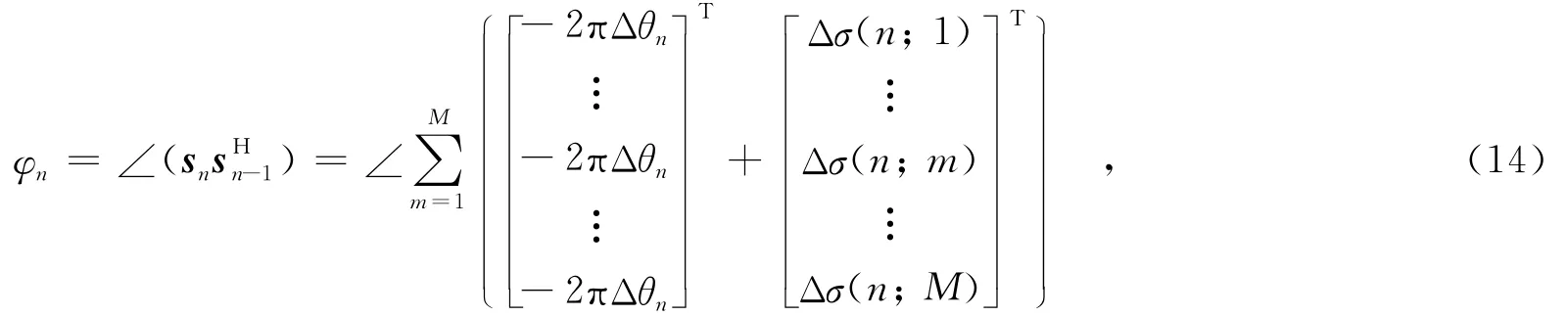
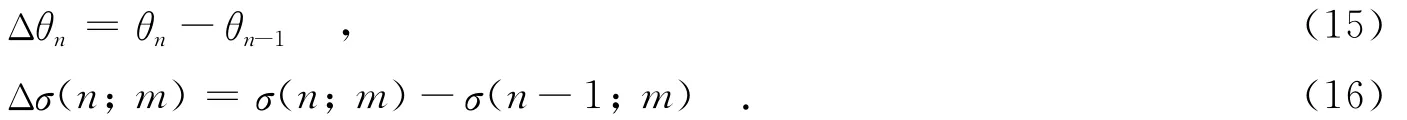
式（15）表明，同一样本信号的不同方位慢时刻，初始相位差Δθn相同，噪声Δσ（n；m）是不同的.上述求和的过程本质上是对初始相位差Δθn的相干积累.化简式（14），可得

经过两次相干积累后，信号相位变为

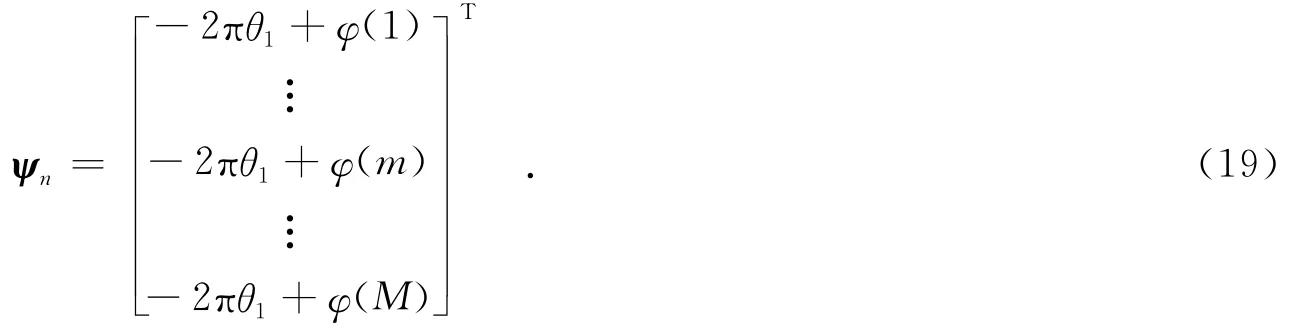
2.5 相位误差的补偿

ψn除了包含相位误差φ（m）外，还包含一个常数相位项θ1，它的存在对图像的聚焦没有影响.将距离压缩后的信号统一与

相乘，补偿相位误差，就可以得到聚焦的图像.

前面讨论的多普勒相位、二次相位、随机初相和相位误差的估计均是假设信号中仅含有需要估计的相位项，不考虑其他相位的影响，实际中相位是同时存在的.文中采取迭代处理方法的步骤为：先采用文中的方法进行一次粗补偿，随机初相和相位误差对多普勒相位的影响已经变得很小；再进行多普勒相位的估计会提高精度，多普勒相位估计精度的提高，可以更准确地估计二次相位和相位误差；二次相位和相位误差估计精度的提高，又可以更进一步提高多普勒相位的补偿，如此迭代至相位误差估计精度达到指定要求为止.

3 运算复杂度分析

通过统计各算法中的复数乘法运算来进行运算复杂度分析.各步骤运算量如表1所示.表1只给出了1次迭代需要的复乘运算，总的运算量为每次迭代所需的运算量乘以迭代次数.表1说明，文中方法与传统方法的运算复杂度的差异主要是在二次相位补偿和初始相位补偿.二次相位补偿中，γk的范围一般较小，特显点样本个数L一般也较小，因此二次相位补偿的运算量是可以接受的.初始相位补偿中，两种方法的运算复杂度在同一数量级，实际处理中的运算效率接近.

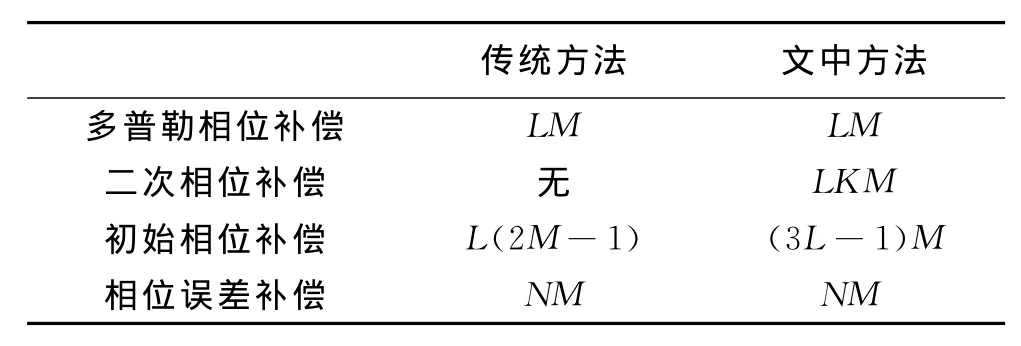
表1 算法运算复杂度

4 算法流程

机动目标ISAR自聚焦算法的处理流程如图2所示，该算法的流程步骤如下：

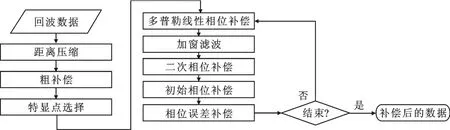
图2 文中算法的流程图

（1）距离压缩.首先对原始回波数据进行距离压缩和包络对齐.

（2）粗补偿.利用第2节的方法，对距离压缩后的数据进行粗补偿.

（3）特显点单元选择.按照信号强度从大到小排列，筛选出高信噪比的距离单元，构成样本信号.

（4）多普勒线性相位补偿.将信号的一维方位像圆平移至图像中心消除多普勒相位的影响.

（5）加窗滤波.预先设定逐步减小的窗长进行加窗滤波以提高样本的信杂噪比.

（6）二次相位补偿.通过对调频率的饱和搜索，利用式（12）补偿二次相位项.

（7）初始相位补偿.利用式（17）和式（18）估计，并补偿随机初始相位.

（8）相位误差补偿.利用式（20）估计，并补偿相位误差.

（9）重复迭代步骤（4）～（8），直到估计达到收敛精度.

5 数据处理及结果分析

5.1 仿真数据处理及结果分析

实验数据来自美国Naval Research Lab提供的B727S仿真数据.主要参数如下：中心频率为9GHz，带宽为150MHz，脉冲重复频率为20kHz.仿真数据具有较高的信噪比，并且已经过包络对齐和运动补偿.图3（a）所示为采用距离－多普勒成像方法得到的成像结果，由于目标的机动特性，图像中存在严重的散焦.

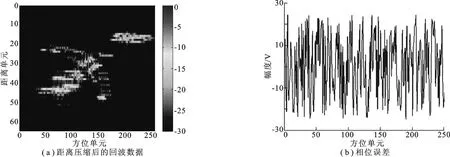
图3 原始数据成像及添加的相位误差

在仿真数据中，加入如图3（b）所示的随机相位误差，变化范围为[－8π，8π].采用相同的样本和相同的迭代次数，利用两种自聚焦方法进行处理，对所有距离单元进行短时傅里叶变换（STFT），选取不同的成像时刻T1、T2和T3，得到图4所示成像结果，图中均为dB图.两种方法均能估计出随机相位误差，但传统方法的一些距离单元有较严重的散焦现象，如图4圆圈中的区域.这是因为传统自聚焦方法没有考虑目标机动引入的二次相位对相位误差的影响，使得相位误差的估计精度不高.文中方法机动引入的二次相位补偿后，再对相位误差进行估计，估计精度高于传统方法，并通过多次迭代处理进一步提高了相位误差的估计精度，最终得到聚焦效果较理想的图像.

在相同的随机相位误差条件下，添加随机复高斯白噪声得到不同信噪比条件下的数据，采用两种自聚焦方法得到图5所示结果.在低信噪比条件下，传统方法聚焦效果不理想，文中方法聚焦效果较好.随着信噪比的提高，两种方法对相位误差的估计精度也提高.在相同的信噪比条件下，文中方法的聚焦精度均优于传统方法，说明文中方法对噪声的容忍性较好.由于文中所提算法在对初始相位的估计过程中，通过对样本信号的二次相干积累，有效降低了噪声对随机初相估计精度的影响，并通过多次迭代直到相位误差收敛到所需精度要求为止，提高了算法的鲁棒性.采用图像熵和均方误差来定量分析两种方法的聚焦性能，如图6所示.横坐标表示不同的信噪比，纵坐标表示相位误差的估计值与真实值的均方误差.图6中曲线为经过200次蒙特卡洛实验后的结果，其计算公式为

图4 两种方法的成像结果

图5 不同时刻的成像结果

5.2 实测数据处理结果

本次实验利用实测数据验证算法的有效性.观测目标为雅克－42飞机.信号带宽为400MHz，载频为C波段.分别采用两种方法自聚焦处理后，得到图7所示的时频成像结果.在不同的成像中心时刻，目标的姿态有明显的变化.传统方法在不同的成像中心时刻有不同程度的散焦（图中圈中的部分），文中方法较好地提高了目标的聚焦性能，图像熵均小于传统方法，聚焦效果较理想.

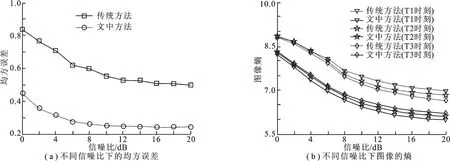
图6 不同信噪比下算法的性能

图7 实测数据处理结果

6 结束语

机动目标的合成孔径阵列流形复杂，且难以精确已知.传统的自聚焦方法不能有效地补偿机动引入的二次调频相位，聚焦效果不理想.当信噪比低时，散焦现象更严重.笔者提出了一种机动目标自聚焦新方法，该方法通过一维方位像圆平移至图像中心，消除多普勒线性相位对相位误差估计精度的影响；通过线性饱和搜索获得方位调频率的最优估计，进而实现二次相位项的补偿；通过对所有样本信号的相干积累，降低了噪声的影响，实现了初始相位的精确估计；最后通过多次迭代处理，提高了相位误差估计精度.仿真和实测数据处理结果表明，文中方法具有比传统方法更好的聚焦效果和噪声容忍性.

[1] 保铮，邢孟道，王彤.雷达成像技术[M].北京：电子工业出版社，2005.

[2] Chen C C，Andrews H C.Target－motion－induced Radar Imaging[J].IEEE Transactions on Aerospace and Electronic System，1980，16（1）：2－14.

[3] Wang G Y，Bao Z.The Minimum Entropy Criterion of Range Alignment in ISAR Motion Compensation [C]//Proceedings of Radar Systems（IEE Conference Publication No 449）.Stevenage：IEE，1997：236－239.

[4] Xing M D，Wu R B，Lan J Q，et al.Migration through Resolution Cell Composition in ISAR Imaging[J].IEEE Geoscience and Remote Sensing Letters，2004，1（2）：141－144.

[5] Zhang L，Qiao Z，Xing M D，et al.Arobust Motion Compensation Approach for UAV SAR Imagery[J].IEEE Transactions on Geoscience and Remote Sensing，2012，50（8）：3202－3218.

[6] Falcone P，Colone F，Lombardo P，et al.WiFi－based Passive ISAR for High Resolution Cross－range Profiling of Moving Targets[C]//9th European Conference on Synthetic Aperture Radar.Piscataway：IEEE，2012：279－282.

[7] Jiang R，Zhu D，Shen M，et al.Synthetic Aperture Radar Autofocus Based on Projection Approximation Subspace Tracking[J].IET Radar，Sonar and Navigation，2012，6（6）：465－471.

[8] Joachim H，Ender G.Autofocusing ISAR Images Via Sparse Representation[C]//9th European Conference on Synthetic Aperture Radar.Piscataway：IEEE，2012：203－206.

[9] Brisken S，Martorella M，Mathy T，et al.Multistatic ISAR Autofocussing Using Image Contrast Optimization [C]//IET International Conference on Radar Systems.Stevenage：IET，2012：1623.

[10] Ye W，Yeo T，Bao Z.Weighted Least－square Estimation of Phase Errors for SAR/ISAR Autofocus [J].IEEE Transactions on Geoscience and Remote Sensing，1999，37（5）：2488－2494.

[11] Jakowatz C，Wahl D.Eigenvector Method for Maximum－likelihood Estimation of Phase Errors in Synthetic－apertureradar Imagery[J].Journal of the Optical Society of America，1993，10（12）：2539－2546.

[12] Wahl D，Eichel P H，Ghiglia D C，et al.Phase Gradient Autofocus—a Robust Tool for High Resolution SAR Phase Correction[J].IEEE Transactions on Aerospace and Electronic Systems，1994，30（3）：827－834.