利用稀疏非负矩阵分解的大转角SAR成像方法

许 然，李亚超，邢孟道

（西安电子科技大学 雷 达信号处理国家重点实验室，陕西 西 安 710071）

合成孔径雷达（Synthetic Aperture Radar，SAR）通过发射宽带脉冲信号并进行方位相干积累，实现二维（距离向和方位向）高分辨成像，在地表测绘和目标识别等领域得到了广泛应用.为了使SAR图像包含丰富的特征信息和保证目标的检测识别概率，最直接的途径就是提高成像分辨率.近年来宽带射频半导体技术的发展使得SAR能够取得亚米级，甚至厘米级的距离分辨率.而与此同时，为了在方位向获得与距离向同等级别的分辨能力，则需要比常规SAR更宽角度的方位积累，即进行大转角SAR成像（Wide Angle SAR，WASAR）[1].

在进行大转角SAR成像的情况下，成像处理将变得困难.首先，回波数据的二维频域支撑区将是占据很大角度范围的同心圆环扇形区域，而不再用矩形网格近似；其次，大的相干积累角度意味着散射点在距离向和方位向的徙动现象严重，需要加以补偿；此外，由于积累角度很大，必须考虑目标的各向散射异性，即各个散射点的回波能量分布在长方位孔径上，但并不一致.这些问题使得常规小转角下的理想假设不再成立，因此不能直接使用如极坐标格式算法（PFA）等基于傅里叶变换的成像算法.针对大转角SAR成像问题，常用方法是将整个成像间隔分为若干个有重叠区段的子孔径进行处理，这样每块子数据便满足小转角的近似假设.文献[2]认为子块数据满足线性等均匀采样条件，散射点未发生走动，可直接利用快速傅氏变换算法（FFT）进行成像，然后再进行旋转融合获得大转角综合图像，但在高分辨率大目标情况下，不徙动条件难以满足；文献[1，3]用逆问题对成像处理进行描述，构建带有正则化稀疏约束的最优化问题，对每块子孔径数据分别迭代求解成像再取最大值融合，能够一定程度地增强二维分辨能力.但该方法会产生虚假点，需要构建复杂的成像投影算子，并且对计算机存储和计算性能要求很高；文献[4]针对WASAR中二维信号缺失的问题，提出了一种自适应幅相估计的方法实现超分辨成像，但其谱估计的精度在很大程度上依赖于较高的信噪比.

非负矩阵分解（Non－negative Matrix Factorization，NMF）是在所有元素非负性条件下的一种矩阵分解方法，可以获得更直观和更符合人脑认知的加性基表示，其作为一种稳健的特征降维分析工具，被广泛应用于信号处理和模式识别等领域[5－7].在遥感探测方面，NMF也得到了一定的关注[8－9]，但并没有在雷达成像领域的应用.笔者提出了一种基于稀疏NMF的大转角SAR成像算法，首先将全孔径划分为互有重叠的子孔径成像段以满足短孔径假设条件，然后采用PFA算法获得目标在各个不同方位角的子孔径图像，再通过构造带有稀疏增强的正则项约束的NMF目标函数，将子图像映射到NMF子空间，完成全孔径图像综合与稀疏特性增强.该方法不需要构造成像逆算子，采用改进的乘性迭代算法保证收敛性与非负性，能够在有效提高图像信噪（杂）比的同时，获得特征信息更清晰的目标图像.

1 大转角雷达成像模型

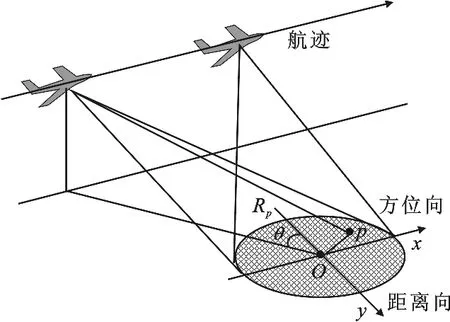
图1 聚束SAR模式示意图

提高刚体目标的成像时间，可以获得更丰富的散射信息，有利于目标的检测和识别.例如，对地面目标可采用高分辨聚束SAR成像模式（如图1所示），其本质是通过增加相干积累角以提高方位分辨率，并获得多角度雷达散射截面（RCS）信息.在常规短孔径近似下，目标区域被认为是由若干各向同性的散射点组成的，不同点的散射系数仅是其空域位置的函数；而在宽角度成像模式下，这种近似将不再合理.因为通常在实际情况下，大多数场景点目标是各向异性的，即散射系数还与方位观测角存在耦合关系.令雷达发射脉冲为p（t），对于场景中某一点p，其在方位角θ处的回波可表示为

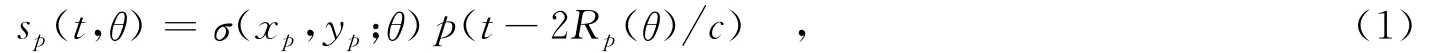
其中，Rp（θ）为目标点与雷达相位中心在方位θ处的斜距，σ（xp，yp；θ）是目标点的散射系数，c是光速，（xp，yp）是点p在斜距平面内的投影坐标.实际上，目标点与雷达视线的擦地角也随θ变化，对散射系数产生额外的微小调制，但在小场景远场假设下，这种变化可以忽略.如果雷达发射线性调频信号为

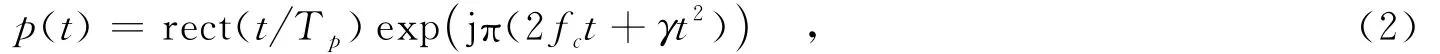
其中，rect（·）表示矩形窗函数；Tp为脉冲宽度；γ＝B Tp，为调频率，B为信号带宽.则雷达接收到的场景总回波在经过去载频、匹配滤波和运动补偿等预处理后，可以表示为

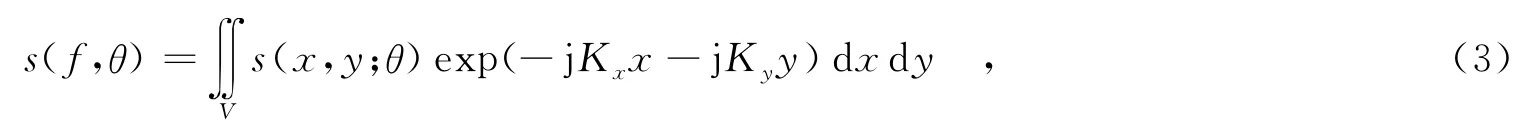
其中，V 代 表雷达照射区域；Kx＝4πfsinθc，为距离向波数；Ky＝4πfcosθc，为方位向波数；θ∈[－Θ2，Θ2]，表示方位观测角变化范围；f∈ [fc－B 2，fc＋B 2]，为信号频率.常规短孔径成像模式下，信号的二维波数谱体现为角度支撑不大的扇区（通常不超过10°），给定Θ便可以直接利用PFA算法完成极坐标到直角坐标的插值去除距离和方位的耦合，再采用IFFT进行成像.然而在大转角情况下，这种二维耦合现象严重，波数谱占据了很大的角度区间，其支撑区接近于同心圆环（如图2所示），有效插值区域存在上限，进而出现频谱利用率较低的情况，使得直接使用PFA有一定的角度限制[10]；反向传播（Back－Projection，BP）算法虽然没有使用约束条件，但全孔径相干积分会使能量平均到整个成像区间，使得弱散射点被抑制，抗噪性能不强，而且全孔径BP算法运算量较大.为了解决这些问题，通常是牺牲方位分辨率，将整个全孔径划分为若干子孔径以保证PFA性能，同时降低各向异性效应，然后分别成像，获得不同观测角下的子图像，再最终完成旋转融合.子孔径数据可以表示为

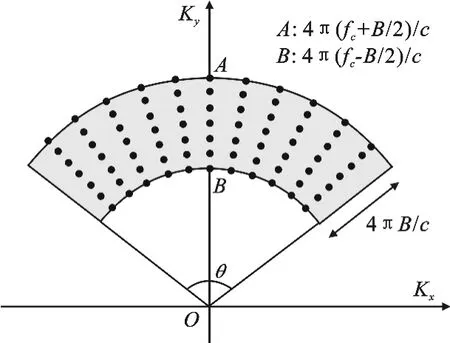
图2 WASAR二维波数域

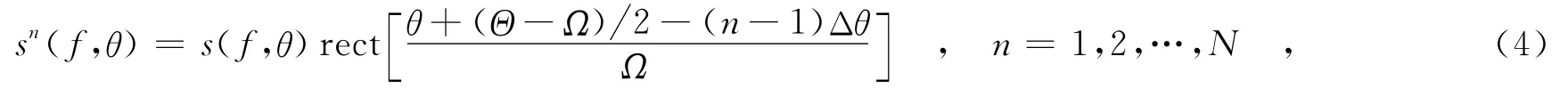
其中，N表示子数据总块数，Ω表示子孔径方位积累角，Δθ表示子孔径间的角度差.若令Δθ＜Ω，则相邻子孔径间有Ω－Δθ大小的角度重叠.由于PFA算法会损失一定的频谱，重叠可以防止子孔径间的积累角度出现较大断裂，提高谱利用率.其次，这种划分能平滑子图像间的散射系数变化，同时保护较短方位响应范围的弱散射点，防止其相位历程被切断而造成能量弱化和分辨能力降低.选择子孔径的长度时，应在满足PFA使用条件和保证方位分辨率的情况下，尽量缩短孔径长度以减小各向异性对成像质量的影响.

接下来对各个子孔径数据分别使用PFA算法进行成像，即将sn（f，θ）进行极坐标到直角坐标系的插值.通常是分别沿着距离维和方位维完成一维插值重采样，然后再对插值后矩形网格数据进行二维IFFT变换得到子图像.为了抑制副瓣可以在该步骤中加入窗函数.子图像代表了目标在不同方位观测角处的SAR图像，要获得全孔径特征信息，则应对子图像旋转到统一坐标系配准后再进行全孔径图像综合.最简单也最容易理解的方法是，对所有配准子图像直接求和.这种方式可以直观地反映目标的特征信息，但弱散射点的能量不能够得到很好的体现，尤其在低信噪比情况下目标和噪声都进行了非相干叠加，使得图像质量不高；文献[1]采用了基于一般似然比检验（GLRT）的方法，将综合图像中的像素灰度定义为所有子图像中该像素位置处的灰度最大值，这种方法获得的目标图像特征信息更清晰，但抗噪性仍然不高，且破坏了目标原始的散射能量分布，这对于目标散射信息提取和目标识别十分不利.因此，笔者提出了一种基于稀疏非负矩阵分解的全孔径图像综合方法，在图像域通过加入稀疏约束的迭代优化，融合各个子孔径下的目标散射信息，抑制噪声（杂波）的同时，获取散射特征信息增强的全孔径SAR图像，提高图像的可解译能力.

2 基于稀疏NMF的全孔径图像综合

非负矩阵分解是以所有矩阵元素均非负作为约束条件的矩阵分解方法，其问题可以描述为：已知一个非负矩阵V∈Rm×n，求非负矩阵W ∈Rm×r和非负矩阵H ∈Rr×n，使得

其中，r满足（m＋n）r＜mn.NMF可看做是将原始数据V映射到低维特征子空间中，在减少数据量的同时，获得基于数据自身的特征基向量的线性表示，而这种表示的基向量本身和权值系数也满足非负条件.NMF算法得到的基向量组W具有一定的正交性和稀疏性，即体现了原始数据的局部特征.那么由非负的线性组合来近似表达V，则体现了整体由局部组成的直观认知，具有明确的物理意义.W中基向量的个数r直接决定了特征空间的维数.根据NMF算法的理论，当r＝1时，原始数据V中各个样本均可由子空间的惟一基向量加权近似表示，那么该基向量应尽可能包含原始样本集的完整特征.如果令各个配准后的子孔径图像作为NMF的特征样本输入V，迭代得到惟一基W作为输出的综合全孔径图像，则该图像就包含了目标所有方位观测角下的散射特性.而在NMF算法中加入稀疏约束，可以增强分解结果本身具有的稀疏性，提高散射点的分辨能力，并且抑制旁瓣、噪声和杂波.

目前，已经有很多关于稀疏NMF的研究：文献[11]实现了基于NMF的稀疏编码，但其针对的是分解系数矩阵而不是基矩阵；文献[12]采用了一种定量控制基矩阵或系数矩阵稀疏度的NMF算法，采用l1范数约束，通过梯度下降法进行迭代求解，但每步迭代都需要复杂的稀疏投影操作，且无法保证非负性.相比较于l2范数和l1范数，加以lk范数正则项（k＜1）约束的解具有更稀疏的结构[13].考虑点散射模型下，大转角刚体目标的雷达图像由强散射点组成这一稀疏特性，可采用欧氏距离作为NMF算法的代价函数，并向其中加入对基向量（也就是全孔径图像）的lk范数惩罚（0＜k＜1），可得到如下的最优化问题：

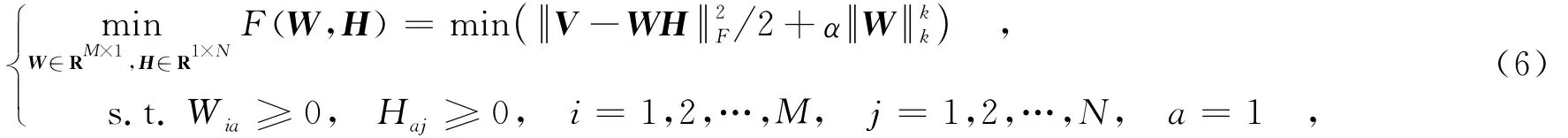
其中，V ＝ [v ，v，v，… ， v]，v＝vec（I），I是由sn（f，θ）经过PFA算法得到的第n幅子图像的灰度矩

123Nnnn阵，vec（·）表示矩阵按列堆叠成列向量操作；W 是 NMF输出的全孔径综合图像幅度向量，其长度M＝Nr×Ncr，Nr和Ncr分别为距离向和方位向采样点数.式（6）中的第1项 V －WH用来控制NMF分解结果与原始数据的拟合误差，αW为稀疏约束正则项，α是惩罚因子，·k代表矩阵元lk范数，定义为大小决定了W的稀疏程度，k越小，则解中非零元素个数越少，也就越稀疏.α和k作为正则化参数，一同起着平衡分解误差与稀疏程度的作用，应根据实际应用场合进行适当选取.当信噪比较低或杂波较强时，需合理采用较大的α和较小的k以增强图像的稀疏度，抑制噪声和杂波的影响.

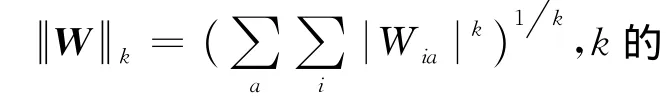
最常用的NMF算法是基于交替迭代的梯度下降算法，即按照下式进行迭代：

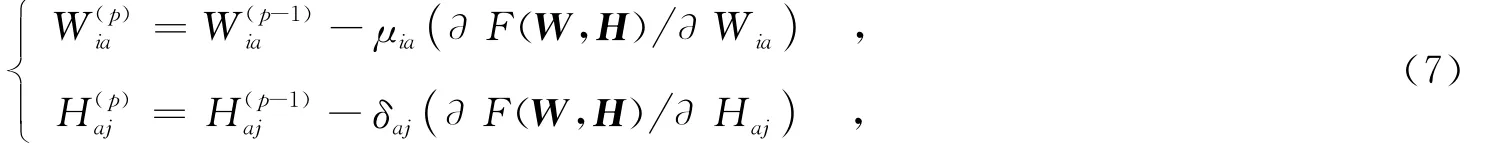
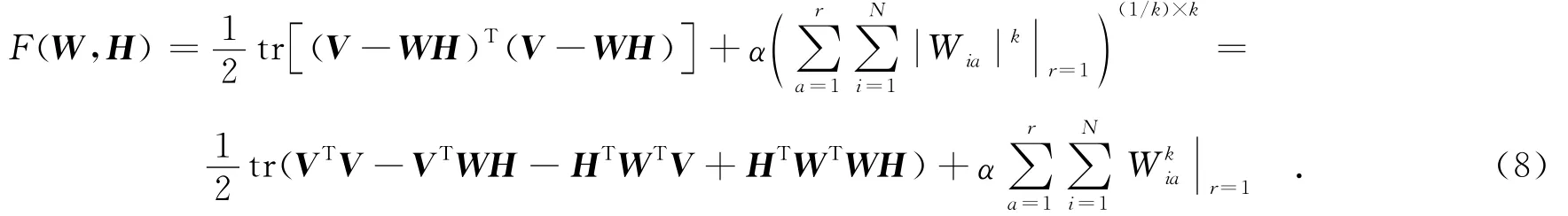
利用矩阵迹函数的性质和求导法则，得到F（W，H）分别对Wia和Haj进行偏导数，即

Lee和Seung令式（7）中的μia和δaj随着W和H的即时迭代结果进行更新，得到一种乘性迭代规则[14]，该算法易于实现，同时保证了非负性和收敛性能.在此基础上，根据具体的代价函数形式，得到修改后的乘性迭代规则.令

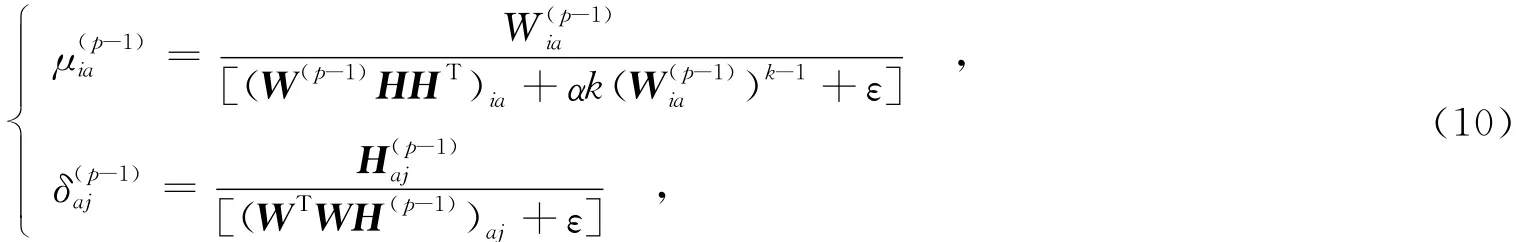
其中，ε是一个很小的正数，例如可以取ε＝10－7，以避免分母为零的情况出现.将式（9）和式（10）代入式（7），可得迭代规则为

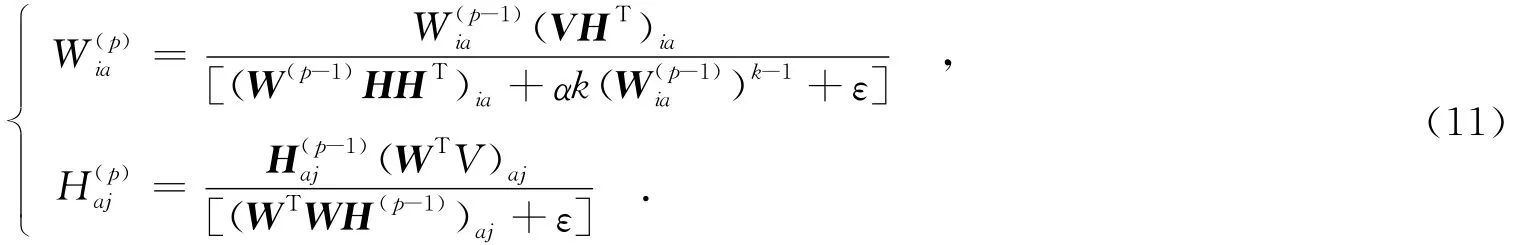
与其他经典NMF算法一样，在每次W迭代后需对其基向量进行归一化操作，这里选择l2范数归一化：

NMF对初始值并不敏感，通常采用非负随机矩阵作为初始即可快速收敛.将迭代终止条件设置为

其中，δ＞0是个很小的门限常数.按照式（11）进行迭代，直至满足式（12）.此时的Wopt经过向量转换为矩阵的逆操作vec－1（Wopt），即得到稀疏特征增强后的全孔径综合图像.文中方法的全孔径图像综合过程如图3所示.值得指出的是，子孔径分割处理和PFA算法不可避免地会降低方位分辨率.但实际上这种综合图像的分辨率并不比全孔径图像差很多，因为通常目标的方位散射响应范围有限，而且存在遮挡等情况，这样成像的分辨率存在上限，不会随着积累角度无限制增加.而通过对图像特征的稀疏增强，可以抑制副瓣与杂波噪声，这在一定程度上改善了散射点的分辨能力.此外，文中方法应用范围不仅局限于WASAR，还可应用于其他成像场合，例如多基地雷达协同成像[15]和大转角ISAR成像等，前者通过方位向数据拼接形成长角度孔径来提高图像分辨率，后者对非机动或合作目标采用长时间跟踪成像模式，可以通过运动补偿等效为WASAR.这些应用本质上都属于宽角度积累问题，均可用文中方法进行成像处理.

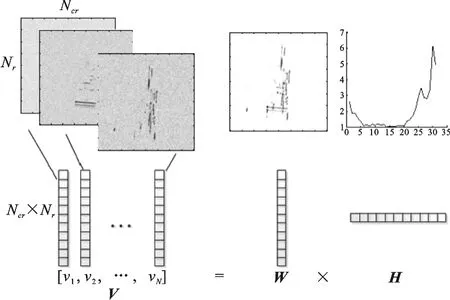
图3 全孔径图像综合示意图

3 实验结果与分析

为了验证文中方法的有效性，采用Backhoe公开数据[16]进行大转角图像重构实验.该数据方位合成角为110°，信号频率范围为7～13GHz，人为地对原始数据加以－5dB的加性高斯白噪声.通过计算该数据的二维频域支撑区范围，可知全孔径PFA算法的有效插值区域过小，无法直接适用.图4（a）给出了全孔径BP算法的成像结果.可以看出，噪声与目标能量相当，极大地影响了其特征辨识.将全孔径分为29个Δθ＝2.9°，每个转角Θ＝28°的子孔径，然后采用PFA算法加汉明窗获得29幅子图像，对子图像旋转配准后，分别使用直接求和叠加方法和文献[1]中的GLRT方法，得到的综合全孔径图像分别如图4（b）和图4（c）所示.与图4（a）相比较，这两种子孔径PFA方法成像结果分辨率稍差，但重叠子孔径处理避免了散射能量的全局平均，尤其对弱散射点保护较好，目标信息更为丰富；但图4（b）中的目标特征在噪声背景下仍不够清晰，图4（c）中目标散射特性虽然较好，但噪声水平依然很高.

图4（d）给出了采用文中方法迭代得到的综合全孔径图像（α＝0.6，k＝0.8）.可以看出，图4（d）中目标结构轮廓清晰，分辨能力得到了提高，噪声和旁瓣被很好地抑制，目标的稀疏特征得到增强.比较这3种子孔径综合图像所对应的灰度向量幅度（图5（a）～（c）所示），GLRT方法得到的图像虽然特征清晰，但噪声也被放大，散射能量分布已被破坏；文中方法在保留散射能量分布情况的同时，令目标图像的特征信息和信噪比量[12]，得到稀疏度sp＝0.903 8，并将该数值设置为稀疏参数，使用文献[12]中的稀疏约束NMF方法（NMFSC），得到综合图像和相应的灰度向量分别如图4（e）和图5（d）所示.与文中方法结果相比，相同稀疏度下，该方法得到的全孔径综合图像噪声水平较高，目标散射信息的表述能力稍差.为了定量比较图像质量，分别对不同方法下的WASAR成像结果进行了图像熵和目标－背景杂波比的衡量比较，其结果如表1所示.可以看出，文中方法结果的熵值最小，TCR最高，表明其目标表征能力最强.另外，笔者还对几种方法在PC平台上的运行时间进行了统计对比，文中方法运算时间虽比图像旋转求和及GLRT方法的耗时，但仍处于一个数量级，对比最终图像质量，这种运算时间上的增加是可以接受的.而与全孔径BP算法和NMFSC方法相比较，文中方法又具有图像质量和运算时间上的双重优势，体现出了良好的性能.

表1 不同方法下的全孔径图像质量对比

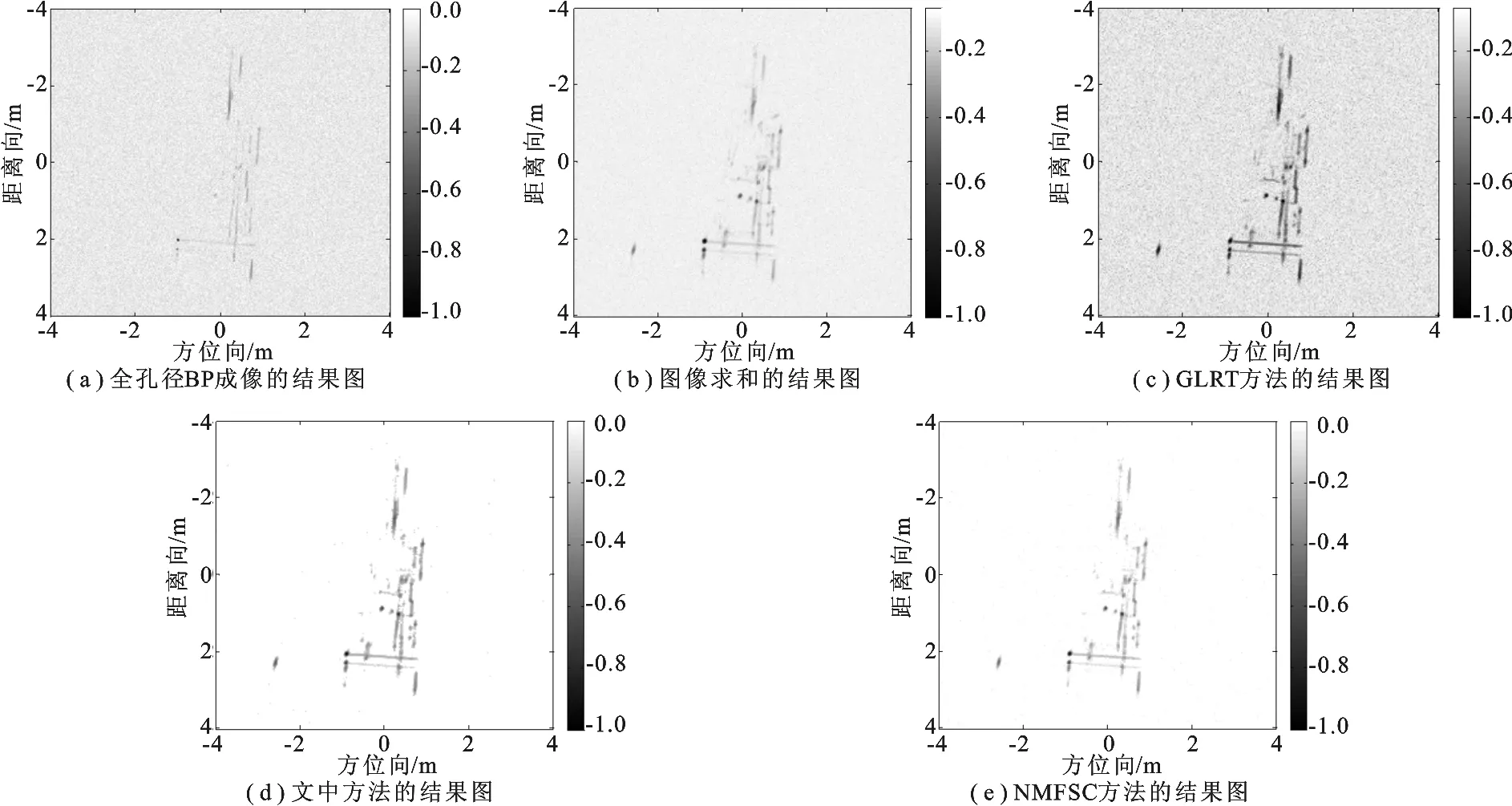
图4 不同方法的全孔径图像

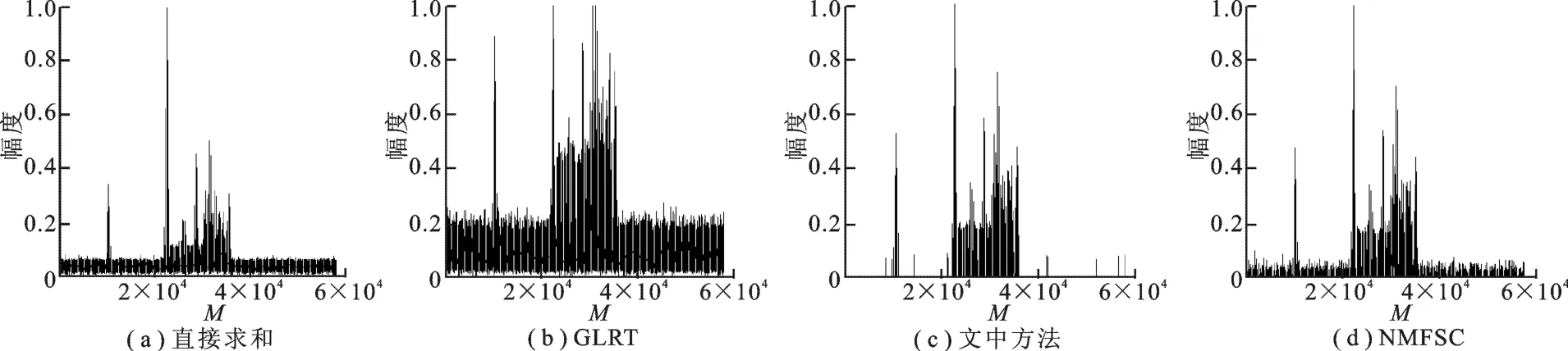
图5 不同方法全孔径图像灰度矢量

4 结束语

提出了一种基于稀疏非负矩阵分解的WASAR成像方法.该方法首先将全孔径分为若干重叠的子孔径，分别进行PFA成像，得到若干不同视角下的子图像，然后构造带有稀疏增强正则项的NMF优化问题，利用改进的乘性迭代规则，对旋转配准后的子图像在NMF子空间进行融合，获得最终的综合全孔径图像.Backhoe数据的处理结果证明了文中方法有很强的目标特征增强能力和去噪能力.文中方法实现简单，但正则化参数的自动选取仍需要进一步研究.

[1] Moses R L，Potter L C，Cetin M.Wide Angle SAR Imaging[C]//Proceedings of SPIE：5427，Algorithms for Synthetic Aperture Radar ImageryⅪ.Bellingham：SPIE，2004：164－175.

[2] Moore T G.A FFT Based Algorithm for the Formation of Wide－angle ISAR Images Using EIP [C]//IEEE International Radar Conference.Piscataway：IEEE，1995：392－395.

[3] Stojanovic I，Cetin M，Karl W C.Joint Space Aspect Reconstruction of Wide－angle SAR Exploiting Sparsity[C]//Proceedings of SPIE：6470，Algorithm for Synthetic Aperture Radar ImageryⅩⅤ.Bellingham：SPIE，2008：697005.

[4] 刘启，洪文，谭维贤，等.宽角合成孔径雷达二维缺失数据自适应幅相估计成像方法 [J].电子与信息学报，2012，34（3）：616－621.Liu Qi，Hong Wen，Tan Weixian，et al.Adaptive Tuning Missing－data Amplitude and Phase Estimation Method in Wide Angle SAR [J].Journal of Electronics ＆Information Technology，2012，34（3）：616－621.

[5] 殷海青，刘红卫.一种基于L1稀疏正则化与非负矩阵分解的盲源信号分离新算法 [J].西安电子科技大学学报，2010，37（5）：835－841.Yin Haiqing，Liu Hongwei.New Blind Source Separation Algorithm Based on L1Sparse Regularization and Nonnegative Matrix Factorization[J].Journal of Xidian University，2010，37（5）：835－841.

[6] Lee D D，Seung H S.Learning the Parts of Objects by Non－negative Matrix Factorization[J].Nature，1999，401（21）：788－791.

[7] Li Y，Ngom A.A New Kernel Non－negative Matrix Factorization and Its Application in Microarray Data Analysis[C]//IEEE Symposium on Computational Intelligence in Bioinformatics and Computational Biology.Piscataway：IEEE，2012：371－378.

[8] Guo R，Zhang L，Xing M，et al.Polarimetric SAR Image Fusion Using Nonnegative Matrix Factorisation and Improved－RGB Model[J].Electronics Letters，2010，46（20）：1399－1401.

[9] Yokoya N，Yairi T，Iwasaki A.Coupled Nonnegative Matrix Factorization Unmixing for Hyperspectral and Multispectral Data Fusion[J].IEEE Transactions on Geoscience and Remote Sensing，2012，50（2）：528－537.

[10] Zhou F，Bai X，Xing M，et al.Analysis for Wide－angle Radar Imaging[J].IET Radar，Sonar and Navigation，2011，5（4）：449－457.

[11] Eggert J，Korner E.Sparse Coding and NMF [C]//IEEE International Conference on Neural Networks.Piscataway：IEEE，2004：2529－2533.

[12] Hoyer P O.Non－negative Matrix Factorization with Sparseness Constraints[J].Journal of Machine Learning Research，2004，4（9）：1457－1469.

[13] Cetin M.Feature－enhanced Synthetic Aperture Radar Imaging[D].Boston：Boston University，2001.

[14] Lee D D，Seung H S.Algorithms for Non－negative Matrix Factorization [C]//Neural Information Processing Systems Conference.Cambridge：Massachusetts Institute of Technology Press，2000：556－562.

[15] Bucciarelli M，Pastina D.Multi－grazing ISAR for Side－view Imaging with Improved Cross－range Resolution [C]//IEEE Radar Conference.Piscataway：IEEE，2011：939－944.

[16] Air Force Research Laboratory.Backhoe Data Sample and Visual Challenge Problem[EB/OL].[2012－08－18].Https：//www.sdms.afrl.af.mil/.