一种参数估计的自适应辅助通道方法

巩继玲，廖桂生，许京伟，朱圣棋

（西安电子科技大学 雷达信号处理国家重点实验室，陕西 西安 710071）

机载雷达处于下视工作状态，面临强地面回波，微弱目标信号将完全淹没在杂波背景中.空时自适应处理联合空域和时域二维信息可以最大限度地提高输出信杂噪比，能够在强杂波背景下进行运动目标检测[1－4].

为了降低对训练样本的需求并提高实时性，研究人员展开了对准最优降维、降秩空时自适应处理技术的广泛研究[5－7].德国的Klemm[8]博士首先分析了正侧阵杂波自由度为N＋K－1的情况，提出了辅助通道降维处理方法，将处理器的维数从NK降到N＋K－1.该方法在无阵元幅相误差时，性能接近最优的全维空时自适应处理，但是若考虑空域误差，杂波自由度增加，性能下降较大.文献[9]提出了3DT方法，具有很好的容差能力，是一种准最优的降维处理方法.文献[10]提出了联合局域处理方法，有效地降低了系统自由度，然而该方法受幅相误差影响较大且存在高旁瓣.文献[11]提出了一种最优且自适应的降秩信号处理结构，性能改善明显且稳健性提高.此外，针对杂波非均匀性、距离依赖性等问题[12－16]，文献[13]提出了一种补偿非均匀性的自适应角度多普勒补偿方法，性能提高了6～10dB；文献[14]提出了一种针对杂波距离依赖性的配准补偿方法，适用于任意阵列构型；文献[15]提出了一种解决共形阵杂波距离依赖性的方法，利用系统参数的估计值进行协方差矩阵估计并对原始回波数据预处理，使其近似满足独立同分布条件；文献[16]提出了一种基于参数估计的自适应补偿方法，相对于常规处理方法，明显改善了杂波对消性能.

传统辅助通道法降低了计算量并且性能较好，但是需要先验已知杂波谱的分布，才能有效地沿杂波脊选取辅助通道.而在实际情况下，雷达的系统参数不是精确已知的，这导致选取的辅助通道偏离实际的杂波谱分布，致使杂波抑制性能下降.针对这一问题，笔者首先利用单一距离单元的回波数据估计杂波谱分布，然后采用最小二乘方法进行参数估计，根据估计的系统参数进行辅助通道的自适应选取并进行降维处理.

1 信号模型

不失一般性，假定雷达天线为经列合成的N元均匀等距线阵（ULA），阵元间距是雷达工作波长的一半.斜视阵几何构型如图1所示.

图1中，Va表示雷达平台的运动速度，θp表示阵面轴线与平台速度之间的夹角，θ表示地面某一散射点与天线阵元之间的方位角，φ表示散射点与天线阵元之间的俯仰角；ψ为相对于天线轴的空间锥角.ψ与方位角θ和俯仰角φ之间满足cosψ＝cosθcosφ.在一个相干脉冲时间（CPI）内发射K个脉冲，因此单一距离单元上某一散射点i的贡献可以表示为

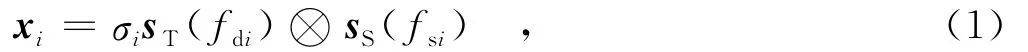
其中，σi为回波幅度，由雷达方程和散射点的后向散射特性决定；si＝sT（fdi）⊗sS（fsi），为对应于第i个散射点的NK×1维的空时导向矢量；⊗ 表示kronecker积；sT（·）和sS（·）分别为时域导向矢量和空域导向矢量，表示为

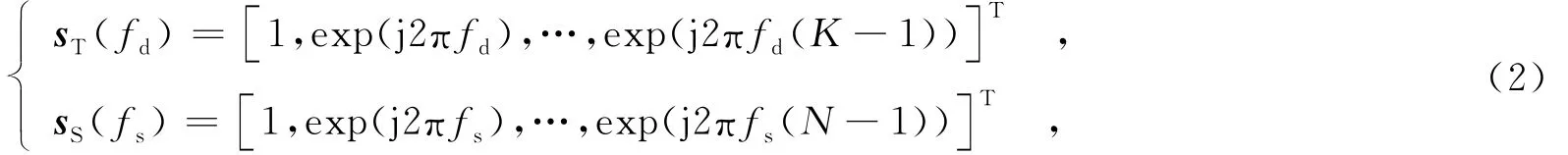
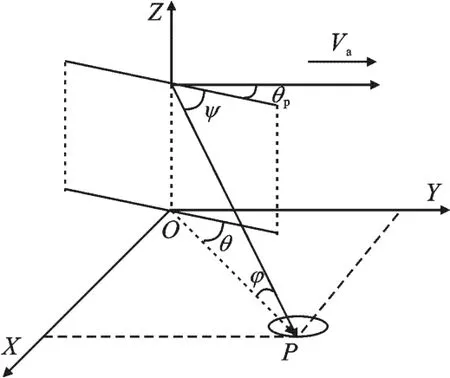
图1 斜视阵几何构型

其中，fd＝2Vcosθcosφλ，为散射点对应的多普勒频率；fs＝dcosθcosφ，为散射点对应的空域频率.时域导向矢量描述了在一个相干脉冲时间内第1个脉冲与其余K－1个脉冲之间相位随时间的变化；空域导向矢量描述了阵元间的相位变化.任意距离单元的回波数据为该距离门内所有散射点的相干叠加，则由Nc个杂波散射点构成的距离单元的空时快拍数据为

对于空时自适应处理器，其最优权wopt＝μR－1s，式中，μ＝1 （ sHR－1s），为归一化因子；向量s指的是目标空时导向矢量；矩阵R指的是杂波协方差矩阵.实际中，协方差矩阵通常由最大似然法估计得到，即

其中，L为距离单元数.当距离单元的数据满足独立同分布的条件且L＞2 NK时，利用式（4）估计得到的协方差矩阵R渐进收敛于真实的杂波协方差矩阵R.空时处理器性能改善（定义为输出信杂噪比与输入信杂噪比的比值）为

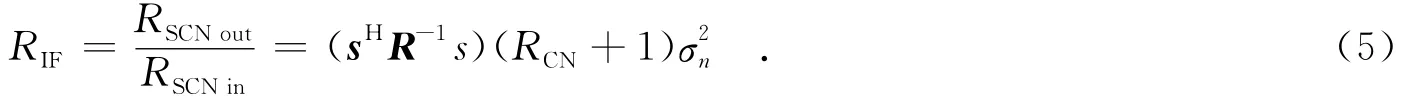
其中，RCN是杂噪比，是输入噪声功率.式（5）从整体上描述了处理器抑制杂波的程度.

2 基于最小二乘参数估计的自适应辅助通道空时处理

辅助通道法的基本原理是在空时二维平面选取与杂波分布匹配的辅助通道，然后利用这些辅助通道的输出对消搜索通道中的杂波分量，这相当于对系统进行一次线性变换.针对传统辅助通道法需要先验知识这一问题，笔者将利用单一距离单元回波数据自身的信息得到参数估计值，无须已知系统参数.

2.1 最小二乘参数估计

由于利用单一距离单元回波数据进行估计得到的协方差矩阵是秩亏的，无法利用MUSIC方法进行谱估计.为解决这个问题，可对回波数据进行时域平滑和空域平滑以得到新的数据矩阵，然后利用MUSIC方法进行谱估计.由于此时得到的谱是粗糙的，所以可利用功率门限检测方法从估计到的杂波谱中提取出大能量的杂波谱并利用这些大能量的杂波谱进行杂波谱线拟合，然后利用最小二乘方法得到参数估计值.

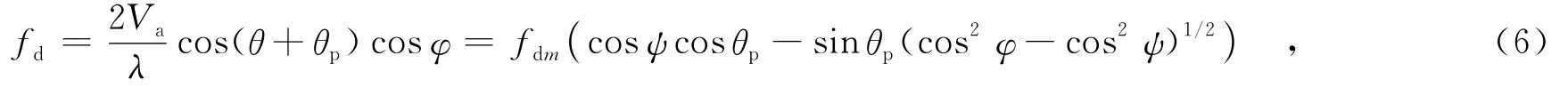
设某单一距离单元上的杂波散射体相应的回波多普勒频率为式中，fdm＝2Vaλ，表示最大多普勒频率；λ表示雷达工作波长.假设在空时二维杂波谱中选择归一化的多普勒频率2fdfr（其中fr为脉冲重复频率）以及锥角余弦cosψ为变量，则式（6）可整理成如下形式：

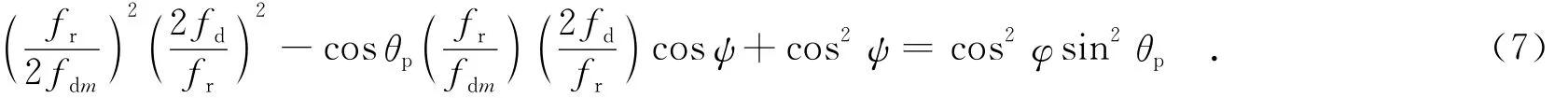
由式（7）可以看出，当阵面偏角θp＝0°时，空时二维杂波谱在2fdfr～cosψ平面内为一条斜带，对应正侧阵；当θp＝90°时，杂波谱为一簇正椭圆，对应前视阵；当0°＜θp＜90°时，杂波谱为一簇斜椭圆，对应斜视阵.如果天线阵面后板具有良好的反射特性，同时近场影响很小，使得后向辐射可忽略不计，则实际的杂波谱只有椭圆的一半.为表述方便，对式（7）进行简化，令

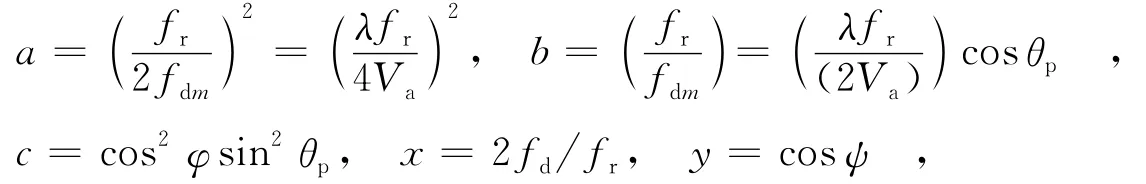
则得到如下的数学简化形式：

其相应的矩阵形式是

其中，A ＝ [x2，－xy，－1]，z＝ [a，b，c]T，b＝－y2.

在实际中雷达的系统参数一般不是精确已知的，所以式（8）中相应的系数也是不精确的.式（8）的数学关系正对应于斜视阵的空时二维杂波谱分布，若关系式不准确，则会造成降维过程中选取的辅助通道与杂波的二维分布不匹配，以致形成的凹口不匹配，导致杂波抑制性能下降.由于最小二乘方法是一种不需要任何先验知识的参数估计方法，所以为了获得较为准确的空时二维杂波分布的数学关系式，可以利用最小二乘方法进行系统参数的估计.式（9）对应的最小二乘解是

利用式（10）得到的最小二乘解即可得到平台运动速度Va、天线阵面偏角θp以及目标距离单元的俯仰角φ的估计值.

2.2 自适应辅助通道法

利用得到的参数估计值计算相应的空时角频率，然后自适应地选取辅助通道并进行降维处理.首先假定降维变换矩阵为T，则回波数据经过降维变换后的数据形式是

辅助通道法自适应处理的输出表达式是

其中，降维变换后的最优权的表达式是

式（13）中，sT＝THs，RT＝E｛xT｝＝THRT，分别是降维变换后的目标空时导向矢量和杂波协方差矩阵.利用辅助通道法进行降维处理大大降低了运算量.笔者提出的方法主要包括参数估计和自适应辅助通道降维处理，因此计算量主要体现在这两方面.假设信号处理过程中的时域自由度是N，空域自由度是K，此时最优处理器的计算量是O（NK）3.由于降维过程中通道数的选取将影响处理的性能，因此在下节对其进行了仿真分析.假设在降维过程中选取的辅助通道数是N＋K＋β（其中β的值可根据实际情况调整），则降维处理过程中的计算量将降低为O（N＋K＋β）3.此外，在参数估计过程中的计算量是O（N1K1）3，其中，N1（N1＜N）和K1（K1＜K）分别为时域和空域平滑子孔径，相对于最优处理器，大大降低了计算量.

3 仿真实验及性能分析

通过以下的几组仿真实验，验证了笔者提出的方法的有效性并对其进行性能分析，同时对比了不同通道个数以及参数有误差时其相应的改善因子和输出功率.仿真实验中所用到的基本仿真参数如表1所示.

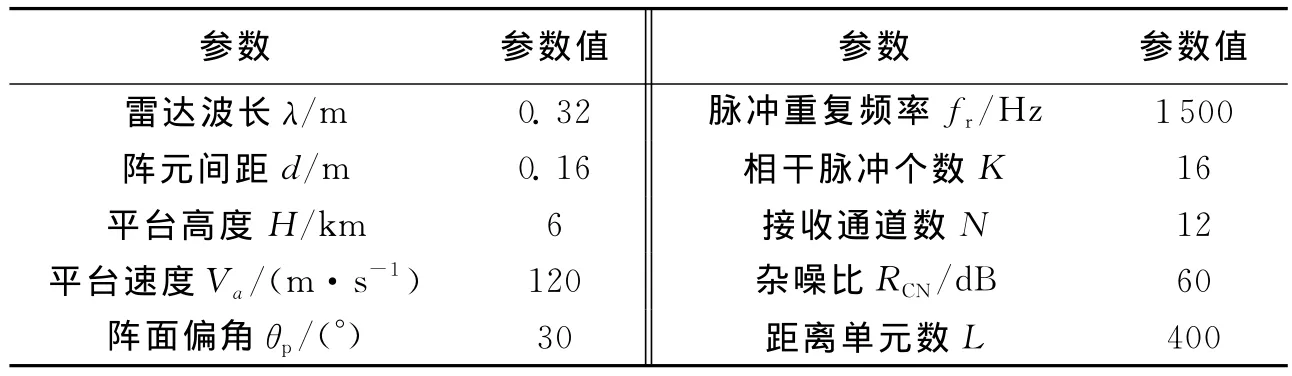
表1 基本仿真参数

3.1 谱估计和辅助通道选取

图2（a）是经过谱峰提取后得到的MUSIC谱，图2（b）是自适应选取的辅助通道的示意图.从图2（a）中可以看出，斜视阵的空时二维杂波谱分布是斜椭圆的一半，与对式（7）的分析相吻合.图2（b）中的实线是利用图2（a）中的杂波谱峰值拟合得到的角度－多普勒曲线，该曲线体现了式（6）的数学关系，即该曲线描绘了给定距离单元上所有散射体的杂波多普勒频率与其波达方向之间的耦合关系.根据得到的拟合曲线，首先利用最小二乘方法进行系统参数估计，然后利用参数估计值得到空时角频率并自适应地选取辅助通道，选取的辅助通道如图2（b）中的圆圈所示.从图2（b）中可以看出，自适应选取的辅助通道与杂波谱的分布曲线匹配，验证了笔者提出方法的有效性.

图2 谱估计和辅助通道示意图

3.2 空时响应性能分析

图3是对应于最优空时自适应处理方法和笔者提出方法的空时二维频率响应图.仿真中天线的主瓣指向为方位90°、俯仰10°，其他仿真参数如表1所示.空时二维频率响应反映了自适应权对杂波的抑制能力，即如果系统能够按照杂波谱的空时二维分布形成相应的斜凹口，并在目标信号处形成主瓣，因此系统具有较好的杂波抑制能力.从图3中可以看出，两种方法均在杂波分布区域形成较深的零陷，实现了杂波的有效抑制，这说明笔者提出的方法具有自适应的对准二维频率响应凹口的能力.此外，主瓣响应特性良好并有较好的增益，避免了因通道选取不准确造成的杂波对消不完全以及目标相消现象.

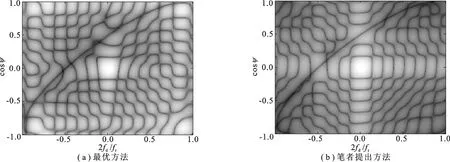
图3 空时二维频率响应图

图4给出了最优空时二维自适应处理方法与笔者提出的方法的改善因子曲线的对比.图中最优方法对应的性能改善是82.67dB，接近于理论值82.83dB（理论值为RCN＋10lg（NK））；对于笔者提出的方法，虽然改善因子曲线在副瓣杂波区有轻微起伏，但是其相对于最优方法的输出信杂噪比损失在3dB以内，性能改善较好.

3.3 辅助通道个数对空时处理性能的影响

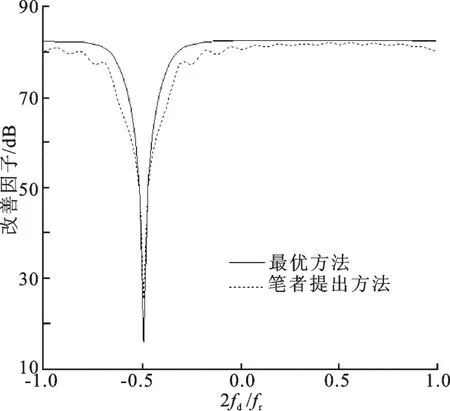
图4 改善因子

图5给出了一组对比实验的仿真结果.以最优方法为参考分别对比了通道个数为N＋K，N＋K＋5，N＋K＋10，N＋K＋15时其相应的改善因子和输出功率.N＋K＋10为笔者所用通道个数.图5（b）中选取距离门号为175～225的50个距离门单元.由图5（a）中可以看出，当通道个数为N＋K时，性能改善较差，主杂波区凹口展宽明显，副瓣杂波区起伏明显；当通道个数为N＋K＋5时，性能改善明显，但是在副瓣杂波区仍有较明显的起伏；当通道个数为N＋K＋10时，副瓣杂波区性能改善较明显，主杂波区无明显改善；当通道个数为N＋K＋15时，性能相对于通道个数为N＋K＋10时没有明显改善.通过仿真实验可以确定，当通道个数为N＋K＋10时，性能改善已较好，此时若再增加通道个数，则性能无明显改善且会增加计算量.假设在第200个距离单元处有一个信噪比为20dB的目标，由图5（b）可见，当通道个数为N＋K时，杂波剩余输出量最大，低信噪比的信号将湮没在杂波中；当通道个数为N＋K＋5时，杂波剩余输出量较前者有明显下降但仍有改善空间；当通道个数为N＋K＋10和N＋K＋15时，两者的杂波剩余输出量相差不多且相对于前者杂波剩余最少.

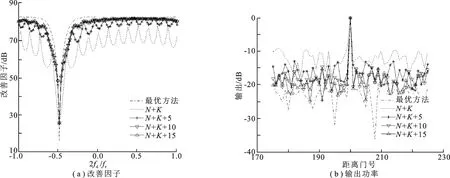
图5 通道数的选取对改善因子和输出功率的影响

3.4 参数误差对空时处理性能的影响

图6给出了一组对比实验的仿真结果，以最优方法为参考分别对比了笔者提出的方法、理想参数以及参数有10%的误差时的改善因子和输出功率.图6（b）中选取了距离门号为175～225的50个距离门单元.由图6（a）可以看出，笔者提出的方法和理想参数对应的改善性能基本一致，相对于最优方法性能损失在3dB以内，验证了笔者提出的方法的有效性；当参数有10%的误差时，其相应的性能改善较差，主杂波区的凹口展宽且副瓣杂波区有明显起伏.图6（b）是4种情况相应的输出功率的对比，可以看出，最优方法的杂波对消性能最好，笔者提出的方法和理想参数对应的杂波对消性能基本一致，而参数有10%的误差时的杂波对消性能较差.

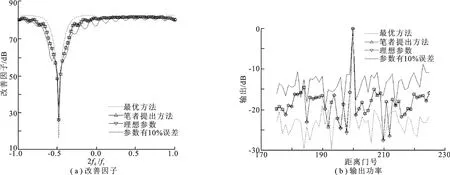
图6 误差对改善因子与输出功率的影响

4 总 结

笔者提出了基于最小二乘参数估计的自适应空时二维辅助通道方法.该方法首先利用回波数据估计杂波分布并采用最小二乘方法估计系统参数，然后自适应选取辅助通道并进行降维空时自适应处理.笔者提出的方法实现了系统参数的精确估计，适用于任意的阵列构型，具有一定的稳健性.仿真实验验证了对于斜视阵，当辅助通道个数为N＋K＋10时可实现有效的杂波抑制.

[1] Melvin W L.A STAP Overview[J].IEEE Aerospace and Electronic Systems Magazine，2004，19（1）：19－35.

[2] Klemm R.Introduction to Space－time Adaptive Processing[J].Electronics ＆ Communication Engineering Journal，1999，11（1）：5－12.

[3] 吕维，王志杰，李建辰，等.空时耦合项对空时自适应处理的影响[J].西安电子科技大学学报，2012，39（2）：207－212.LüWei，Wang Zhijie，Li Jianchen，et al.Influence of the Space－time Coupling Term on STAP[J].Journal of Xidian University，2012，39（2）：207－212.

[4] Zhang Xiaofei，Xu Dazhuan.Angle Estimation in Bistatic MIMO Radar Using Improved Reduced Dimension Capon Algorithm[J].Journal of Systems Engineering and Electronics，2013，24（1）：84－89.

[5] Yang Zhaocheng，de Lamare R C，Li Xiang.L1－Regularized STAP Algorithms with a Generalized Sidelobe Canceler Architecture for Airborne Radar[J].IEEE Transactions on Signal Processing，2012，60（2）：674－686.

[6] Kong Yongfei，Zeng Cao，Liao Guisheng，et al.A New Reduced－Dimension GSC for Target Tracking and Interference Suppression[C]//IEEE CIE International Conference on Radar.Piscataway：IEEE，2011：785－788.

[7] Boizard M，Ginolhac G，Pascal F，et al.A New Tool for Multidimensional Low－rank STAP Filter：Cross HOSVDS[C]//20th European Signal Processing Conference.Piscataway：IEEE，2012：1324－1328.

[8] Klemm R.Adaptive Airborne MTI：an Auxiliary Channel Approach[J].IEE Proceedings.Part F.Communications，Radar and Signal Processing，1987，134（3）：269－276.

[9] 廖桂生，保铮，张玉洪.机载雷达时－空二维自适应处理新方法[J].电子科学学刊，1994，16（3）：225－231.Liao Guisheng，Bao Zheng，Zhang Yuhong.A New Adaptive Spatial－Temporal Processing for Airborne Radars[J].Journal of Electronics，1994，16（3）：225－231.

[10] Wang H，Cai L J.On Adaptive Spatial－Temporal Processing for Airborne Surveillance Radar Systems[J].IEEE Transactions on Aerospace and Electronic Systems，1994，30（3）：660－670.

[11] Guerci J R，Goldstein J S，Reed I S.Optimal and Adaptive Reduced－rank STAP[J].IEEE Transactions on Aerospace

and Electronic Systems，2000，36（2）：647－661.

[12] 孟祥东，王彤，吴建新，等.机载雷达非正侧面阵近程杂波抑制新方法[J].西安电子科技大学学报，2009，36（2）：245－249.Meng Xiangdong，Wang Tong，Wu Jianxin，et al.New Short－range Clutter Suppression Approach for the Non－sidelooking Airborne Radar[J].Journal of Xidian University，2009，36（2）：245－249.

[13] Melvin W L，Davis M E.Adaptive Cancellation Method for Geometry－induced Non－stationary Bistatic Clutter Environments[J].IEEE Transactions on Aerospace and Electronic Systems，2007，43（2）：651－672.

[14] Ries P，Lapierre F D，Verly J G.Geometry－Induced Range－Dependence Compensation for Bistatic STAP with Conformal Arrays[J].IEEE Transactions on Aerospace and Electronic Systems，2011，47（1）：275－294.

[15] Lapierre F D，Ries P，Verly J G.Foundation for Mitigating Range Dependence in Radar Space－Time Adaptive Processing[J].IET Radar，Sonar and Navigation，2009，3（1）：18－29.

[16] Jaffer A G，Ho P T，Himed B.Adaptive Compensation for Conformal Array STAP by Configuration Parameter Estimation[C]//IEEE Radar Conference.Piscataway：IEEE.2006：731－736.