一种同轨双基SAR的非线性CS成像算法

陈士超，邢孟道，保 铮

（西安电子科技大学 雷 达信号处理国家重点实验室，陕西 西 安 710071）

双基地合成孔径雷达（SAR）的发射平台和接收平台安装在不同的载体上，可以获得更多的角度信息，可以提高地面运动目标检测（GMTI）的检测概率，提高了地面高程测量的精度，因此受到了越来越多的关注[1－3].

精确的二维频谱是设计频率域快速成像算法的前提，然而由于双基SAR斜距历程中双根号的存在，使得直接利用驻相点原理无法获得目标精确的二维频谱.时域算法虽然在理论上是最优的，可以实现任意构型双基SAR的精确成像，但运算量很大[4].Cassola等提出的双基快速因式分解后向投影算法（BFFBP）可以大幅度提升时域算法的运算效率，但较之频域算法，运算量仍然较大[5].近年来提出了多种有效的近似双基频谱[6－12]，但它们均为某种条件下的近似频谱.同轨构型双基地SAR编队构形简单，工程上较容易实现，同轨双基TanDEM－X系统已经开始工作，并获取了聚焦效果良好的双基SAR图像和干涉相位图[13].文献[14]在二维波数域提出了一种同轨构型下严格解析的双基频谱，为设计精确快速的成像算法提供了基础.

大斜视角SAR成像可以用来多次重访热点地区，观察角度依赖性强的目标，实现斜前方目标的侦察，可用于导弹制导、战斗机和轰炸机的实时打击，并在打击后评估打击效果等，有非常重要的应用价值[15－16].基于文献[14]提出的严格解析双基频谱，类比单基情形的非线性线调频变标成像算法（NCSA）[17]，笔者提出了一种适用于同轨构型下双基SAR数据处理的NCSA算法，实现大斜视角条件下的双基SAR数据处理.该算法采用非线性变标解决目标的距离徙动问题以及二次距离压缩项的空变问题，获得了理想的成像效果.对比实验进一步验证了所提算法的优越性.

1 信号模型

图1为大斜视角下同轨构型双基SAR的示意图，发射平台Tx和接收平台Rx以相同的速度v匀速直线飞行，θT和θR分别表示目标Pn到发收平台的瞬时斜视角，RT（X）和RR（X）分别为此时发收平台到目标的瞬时斜距，RB为目标到航线的最近距离，β为半双基角，hx为基线长度的一半，X表示平台的位移.

双基SAR的瞬时斜距可以表示为

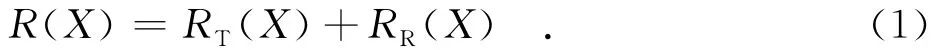
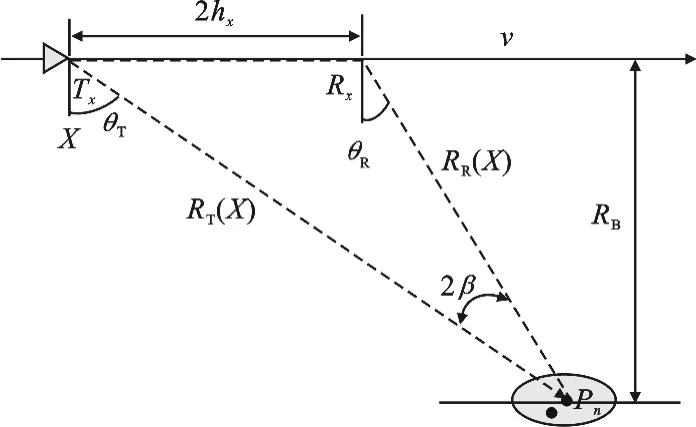
图1 同轨构型双基SAR的几何关系示意图

由图1中的几何关系，有

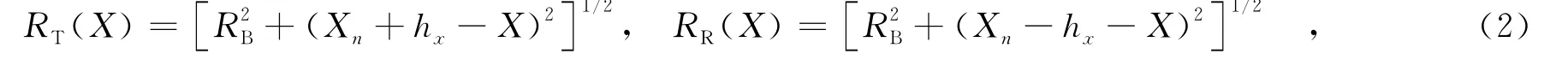
其中，Xn为参考点的方位位置.

假设雷达发射线性调频信号，对回波信号去载频并进行距离脉压后，其信号形式为[16]

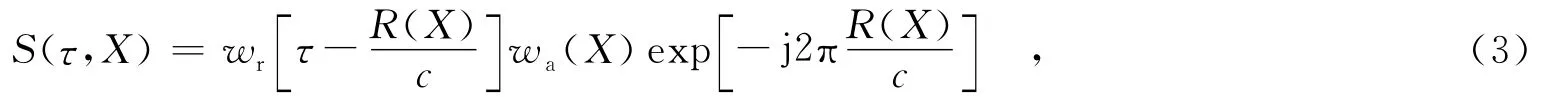
其中，wr（·）为距离包络，wa（·）为方位包络，τ为快时间，c为光速.

对信号进行傅里叶变换，将其变换到距离波数方位位置域，即

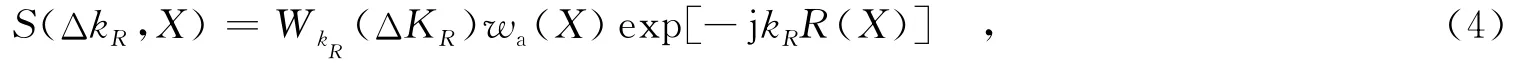
其中，Wk为距离谱包络；ΔkR为距离波数在基频的变化；kR＝ΔkR＋kR，为径向波数；kR＝2πfcc，为距离Rcc波数中心；fc为载频.

对式（4）进行方位向的傅里叶变换，就可以得到同轨双基SAR的二维双基频谱：

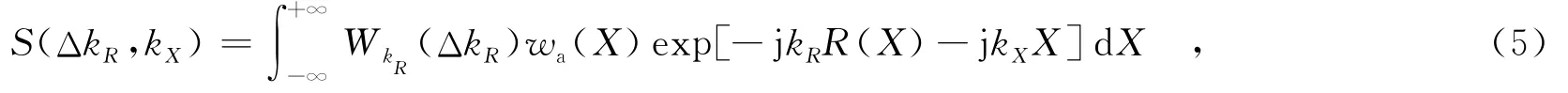
其中，kX为多普勒波数.由于双基SAR斜距历程中双根号的存在，使得直接利用驻相点原理无法求解式（5）以获得双基频谱.

2 同轨双基SAR的非线性CS成像算法

由基于瞬时频率概念的几何关系公式（GBF）方法[9]可以得到式（5）所示的双基SAR点目标二维频谱的解析表达式为

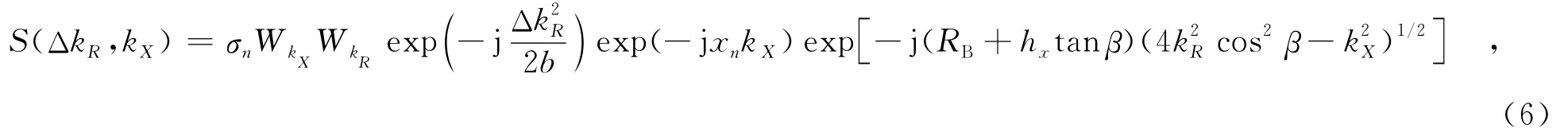
其中，σ 为双基SAR的后向散射系数；W为方位谱包络；1/b＝c2（2πγ），γ为发射信号的调频率；x为目nkXn标所在的方位位置.式（6）中的半双基角β取为文献[14]中成功推导出的严格解析表达式，即

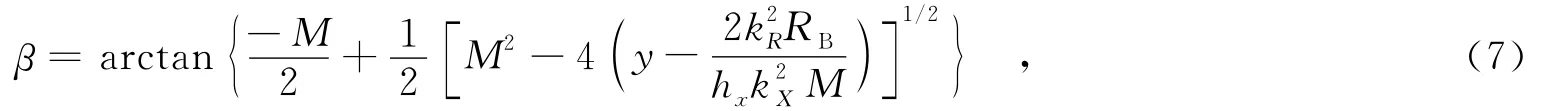
其中，

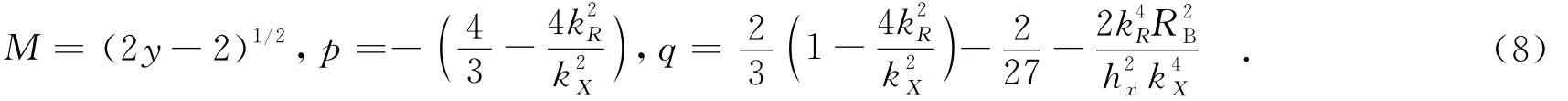
将式（6）在距离波数中心处进行泰勒展开，保留到三次项，有

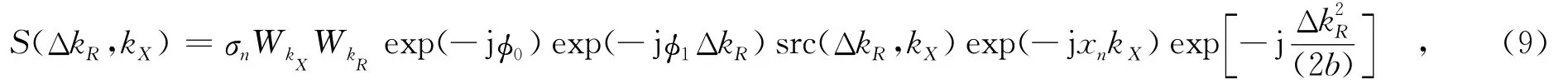
12形式也较为复杂，但当选取hx＝0，β＝0的单基条件时，以上各变量均变为所熟知的单基情形.

将φ1在RB＝Rs处进行泰勒展开，Rs为场景中心处目标到航线的最近距离，取一阶近似，有对应场景中心的距离位置.由式（10）的线性近似所产生的包应的相位误差φ ＝Δkr.为保证近似的合理性，使得偏离参考距离没

errRerr有分辨率下降问题的出现，需B/2]，为距离频率，B为发射信号的带宽，得出rerr＜c （ 4B）.在实际数据处理过程中，首先根据系统参数计算此近似所能容忍的距离向处理宽度，保证rerr在允许的误差范围之内.如果rerr超出容忍上限，则需要将数据沿距离向进行分块处理.

将式（10）代入式（9），整理后信号形式为

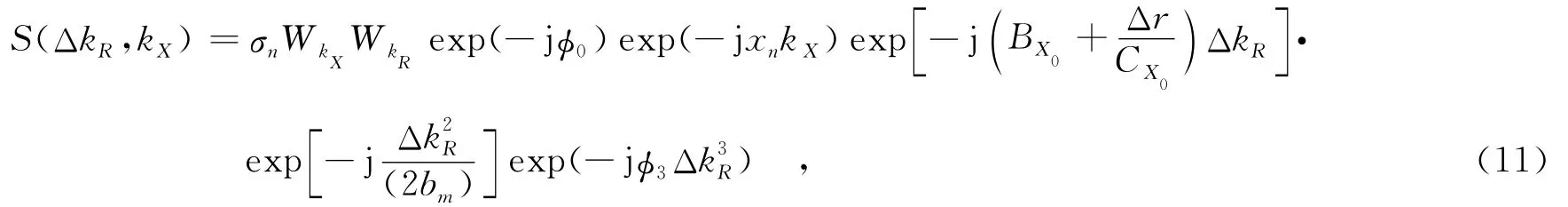
其中，bm＝b （ 1－2bφ2）.在斜视角较小的情形下，二次距离压缩的空变性可以忽略，可以采用场景中心处对应的数值进行补偿[18]，不影响最终的聚焦效果.但在斜视角较大的情形时，如果仍然采用这样的补偿方式，所产生的二次相位残余误差将会大于π/4，影响最终的成像质量.为解决此问题，可将单基情形的NCSA算法引入到同轨双基SAR的数据处理中.

与单基情形时类似，同样认为二次距离压缩（SRC）的三次相位是非空变的，可以采用场景中心处的数值进行补偿，同时引入一个新的三次相位项，构造如下的滤波函数：

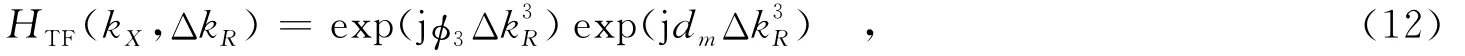
其中，dm数值待定，具体形式将在下文中求解出来.将式（11）与式（12）相乘，所得信号形式为

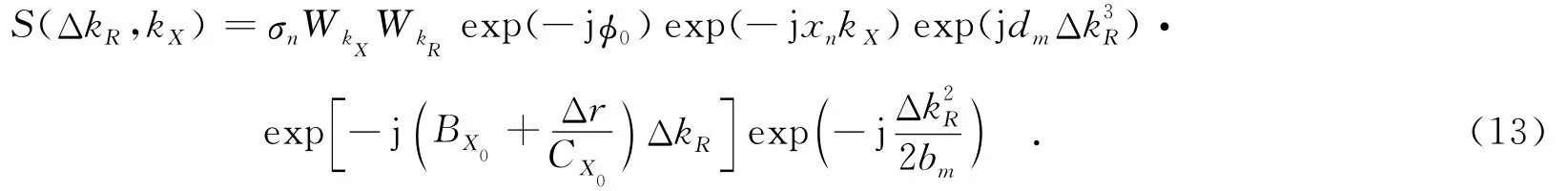
经过公共的距离徙动校正后，对式（13）进行距离向逆傅里叶变换（由于三次相位变化较慢，把它和包络一起看成是慢变函数），可得

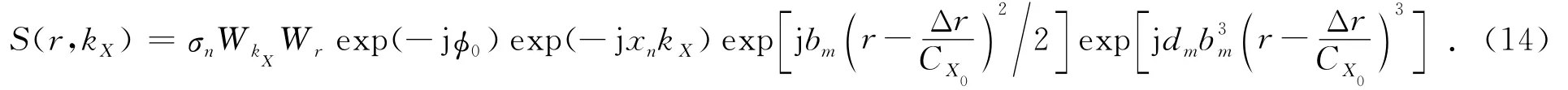
类比单基情形[17]，构造非线性变标函数为

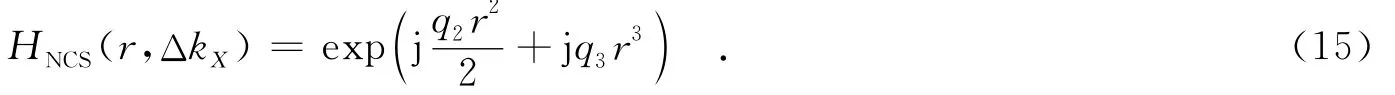
对式（14）和式（15）相乘后的结果进行距离向的傅里叶变换，信号形式为

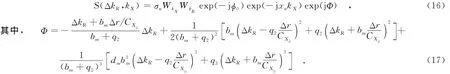
式中的调频率bm不仅随多普勒频率变化，同样也是距离空变的.原始的线频调变标（CS）算法只考虑了调频率随多普勒频率的变化，忽略了其距离空变性[18]，采用场景中心处的数值来代替，在斜视角较小的情况下可以取得满意的成像结果.但当斜视角较大时，补偿带来的二次相位误差将会大于π/4，影响最终的成像质量.非线性CS算法不仅考虑了其随多普勒频率的变化，同样考虑了其距离空变特性，能更精确地反映多普勒调频率的空变性.将调频率bm线性表示为

其中，bm0为bm在Rs处的取值，bs为bm在Rs处对Δr的变化率.

假定以下近似式成立：

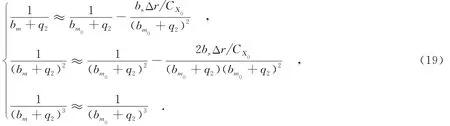
将式（18）和（19）代入式（17），将其整理为

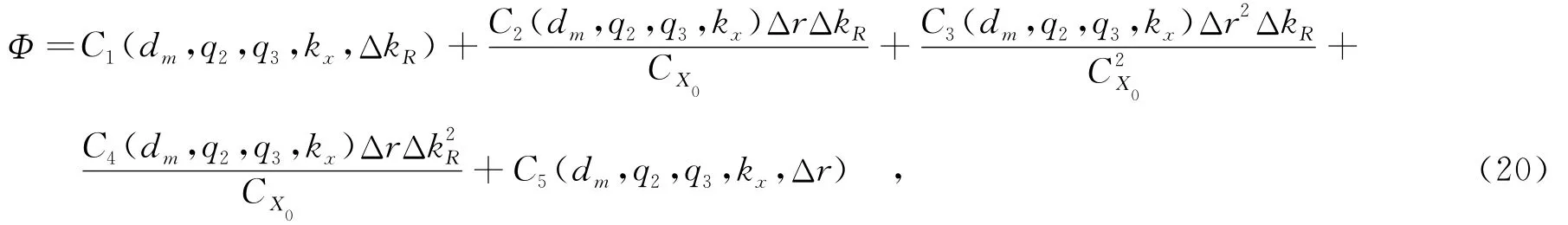
其中，

取C2＝－1/μ，变标因子μ＝CXrefCX，CX＝CX（kX），其中，kX为选取的参考多普勒波数.由式0ref0refref（20）可得，C3为Δr2ΔkR的系数，表征距离徙动随距离的二次空变部分；C4为ΔrΔ的系数，表征二次距离压缩项的空变特性.非线性变标的目的在于消除非理想的二次距离压缩项和距离徙动项的空变性，因此选取交叉项系数C3＝C4＝0，以消除空变项，解方程可得

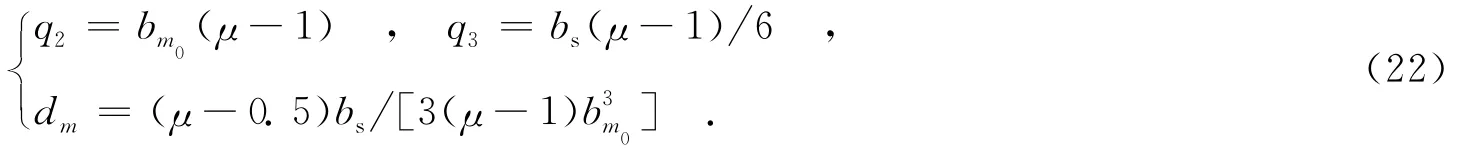
将式（22）得到的各参数代入式（20），经整理后信号形式为

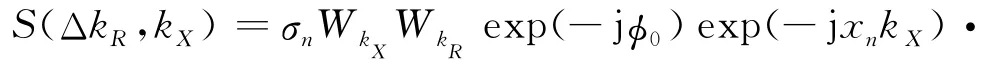
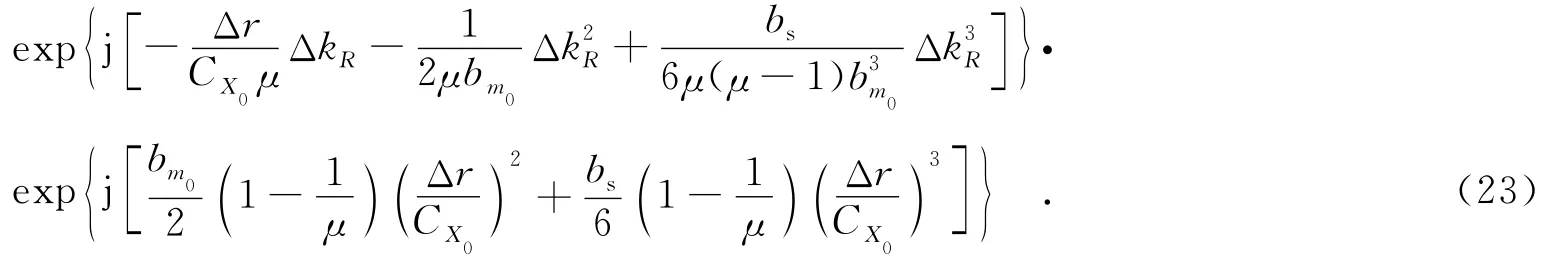
接下来构造距离压缩参考函数

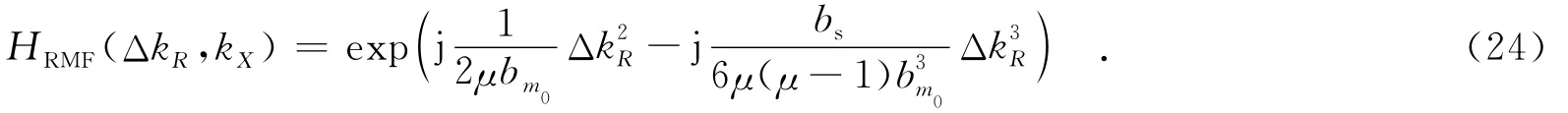
距离压缩后，信号经距离向的逆傅里叶变换到距离多普勒域，进行剩余相位补偿，相位补偿函数为

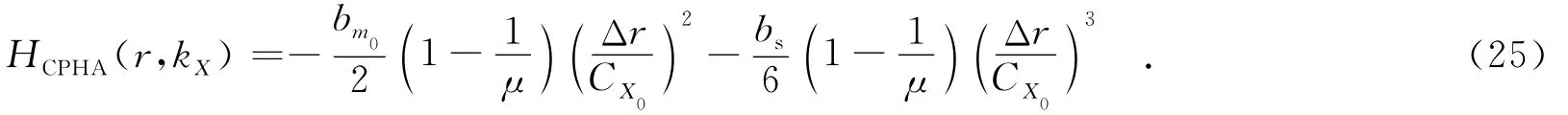
至此，完成距离向的成像处理.需要注意的是，完成距离向处理后，图像在距离向发生了伸缩，因而需要对与距离相关的参数进行相应的调整，以构造正确的方位压缩函数.由式（23）可知，RB应替换为

构造方位压缩参考函数为

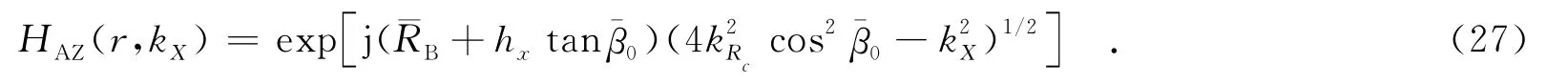
同理，方位压缩参考函数中和距离有关的变量β也对应替换为¯β.接下来经一次方位逆傅里叶变换，完成整个成像过程，整个算法的流程图如图2所示.

从以上分析可知，NCSA的机理在于将信号的相位和参考信号的相位相加，通过调节3个可变参数，使结果成为非空变的，消除多普勒波数和距离波数的耦合项，实现距离徙动校正和SRC的精确补偿.

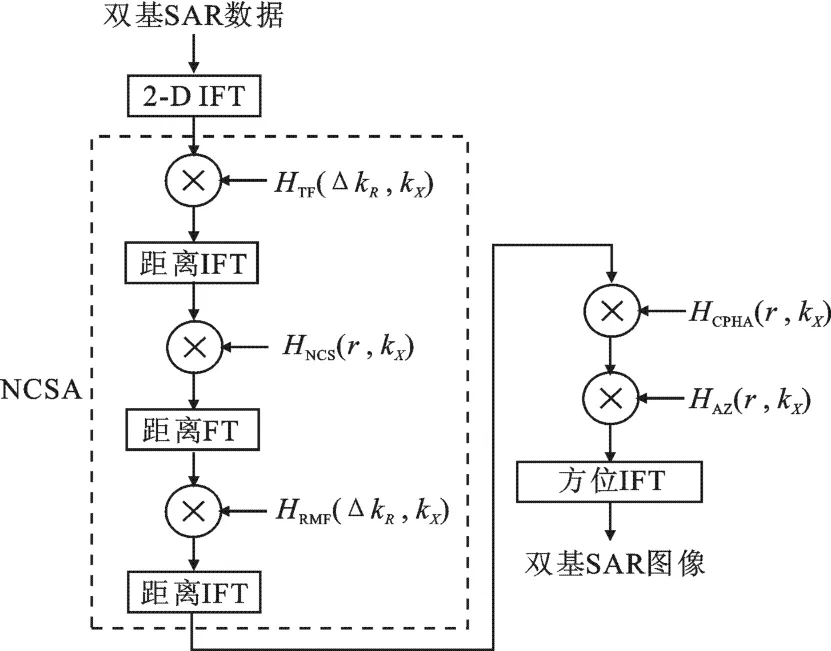
图2 所提同轨双基SAR的NCSA算法流程图

3 仿真实验

为验证文中所述算法的有效性，进行了以下仿真实验.仿真点阵由9个点组成，距离向间隔为400m，方位向间隔为200m，雷达波长为0.03m，天线方位向尺寸为1m，发射信号带宽为200MHz，复采样频率为240MHz，发射平台与接收平台均以110m/s的速度匀速直线飞行，参考作用距离为8 000m，多普勒带宽为220Hz，脉冲重复频率（PRF）为600Hz，基线长度为4 000m，成像中心时刻目标到发射平台和接收平台的斜距分别为17.5km和14.1km，对应的斜视角分别为62.8°和55.3°.在此时的斜视角条件下，若采用适用于小斜视角的CS成像算法，所得的成像结果如图3所示.由图3可见，虽然中心点可以取得理想的聚焦效果，但边缘点目标成像的质量很差.采用文中所述的适用于大斜视角下的NCSA算法对中心点和边缘点进行成像，结果如图4所示.可见场景中心点和边缘点目标均聚焦良好.

为进一步验证文中所述算法的有效性，对比基于级数反演谱（MSR）[8]的大斜视NCSA算法，对应的聚焦效果如图5所示.由图5可见，基于MSR谱的大斜视NCSA算法对中心点可以取得满意的成像结果，但对边缘点所取得的聚焦效果要劣于文中所述算法的.因为虽然MSR谱为一种高精度的双基频谱，但其仍然是一种近似的双基频谱，而文中算法所基于的双基频谱是严格解析的.需要说明的是，MSR的谱精度是可以通过泰勒展开的级数进行控制的，对比实验中斜距历程只展开到三阶，为取得更好的聚焦效果，可以将级数展开到更高的阶数，这里只是用于对比验证所提算法的有效性.两种算法的成像效果评价指标为分辨率、峰值旁瓣比（PSLR）和积分旁瓣比（ISLR），具体结果分别如表1和表2所示.由实验结果可见，两种算法都可以进行精确的距离徙动校正和二次距离压缩.在距离向，两者均可以取得满意的聚焦效果，但在边缘点的方位向聚焦效果有所差别，因为边缘点的方位向聚焦效果取决于算法所基于的频谱精度.文中算法是基于一种严格解析的双基频谱的，频谱精度要高于MSR谱.因此，文中算法方位向的成像效果要好于基于MSR算法所取得的聚焦结果.

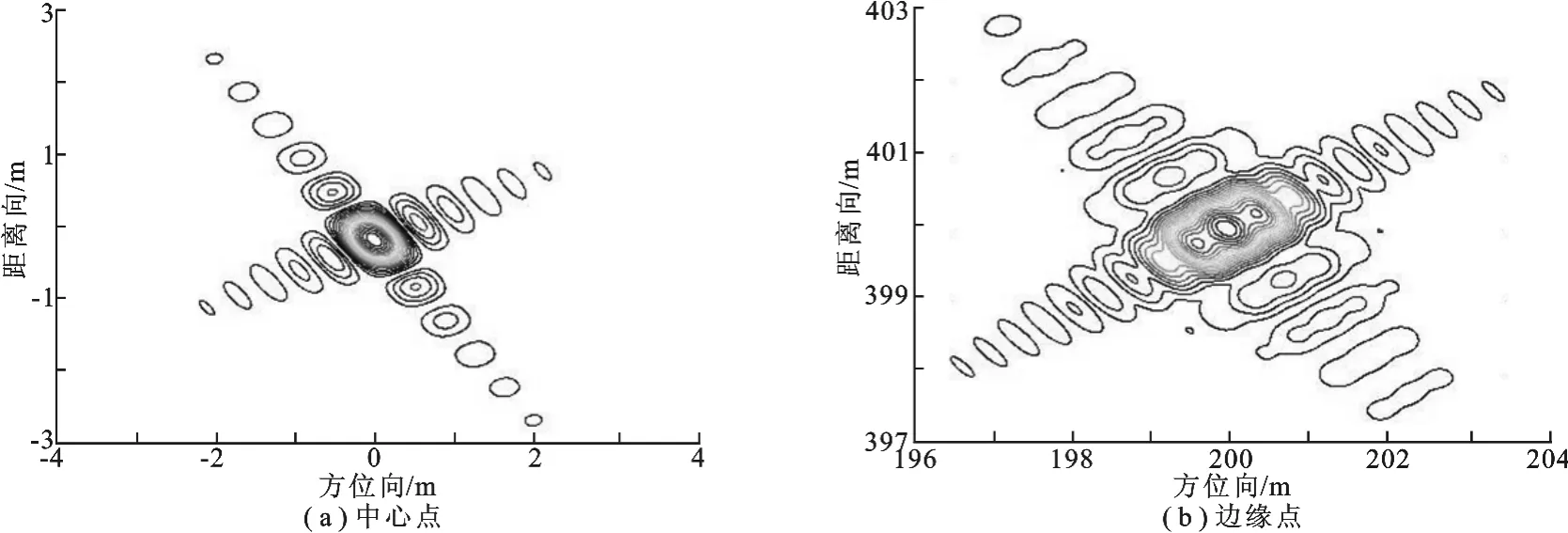
图3 适用于小斜视角的CS成像算法结果

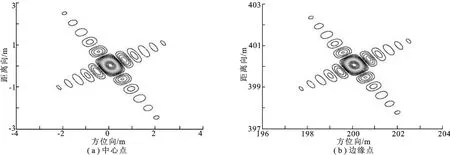
图4 文中所述算法的成像结果

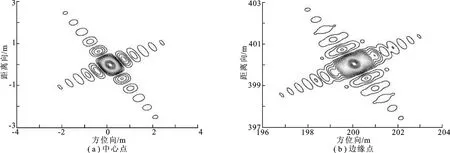
图5 基于MSR谱的非线性CS成像算法的成像结果

表1 文中所提算法的距离向和方位向脉压效果分析

表2 基于MSR谱的非线性CS成像算法的距离向和方位向脉压效果分析

4 结束语

基于一种严格解析的双基频谱，提出了一种非线性的CS成像算法解决同轨双基SAR工作于大斜视情形下时距离徙动和二次距离压缩的空变性问题.不同于传统CS成像算法，所提算法不仅考虑了多普勒调频率随多普勒频率的变化，而且也考虑了其随距离的线性变化，更精确地补偿了二次距离压缩项的空变性，取得了满意的聚焦结果.

[1] He Zhihua，He Feng，Chen Junli，et al.Echo－Domain Phase Synchronization Algorithm for Bistatic SAR in Alternating Bistatic/Ping－Pang Mode[J].IEEE Geoscience and Remote Sensing Letters，2012，9（4）：604－608.

[2] 易予生，张林让，刘昕，等.双站SAR图像几何失真校正方法研究[J].西安电子科技大学学报，2010，37（2）：231－234.Yi Yusheng，Zhang Linrang，Liu Xin，et al.Method for Geometric Distortion Correction of the Bistatic SAR [J].Journal of Xidian University，2010，37（2）：231－234.

[3] Wang Xin，Zhu Daiyin，Mao Xinhua，et al.Space－Variant Filtering for Wavefront Curvature Correction in Polar Formatted Bistatic SAR Image[J].IEEE Transactions on Aerospace and Electronic Systems，2012，48（2）：940－950.

[4] Barber B.Theory of Digital Imaging from Orbit Synthetic Aperture Radar[J].International Journal of Remote Sensing，1985，6（7）：1009－1057.

[5] Rodriguez－Cassola M，Prats P，Krieger G，et al.Efficient Time－domain Image Formation with Precise Topography Accommodation for General Bistatic SAR Configurations[J].IEEE Transactions on Aerospace and Electronic Systems，2011，47（4）：2949－2966.

[6] D'ariad D，Guarnieri A M，Rocca F.Focusing Bistatic Synthetic Aperture Radar Using Dip Move Out[J].IEEE Transactions on Geoscience and Remote Sensing，2004，42（7）：1362－1376.

[7] Wang R，Loffeld O，Neo Y，et al.Extending Loffeld＇s Bistatic Formula for the General Bistatic SAR Configuration[J].IET Radar，Sonar and Navigation，2010，4（1）：74－84.

[8] Neo Y，Wong F，Cumming G I.A Two－dimensional Spectrum for Bistatic SAR Processing Using Series Reversion[J].IEEE Geoscience and Remote Sensing Letters，2007，4（1）：93－96.

[9] Zhang Zhenhua，Xing Mengdao，Ding Jinshan，et al.Focusing Parallel Bistatic SAR Data Using the Analytic Transfer Function in the Wavenumber Domain[J].IEEE Transactions on Geoscience and Remote Sensing，2007，45（11）：3633－3645.

[10] Wang R，Deng Y，Loffeld O，et al.Processing the Azimuth－variant Bistatic SAR Data by Using Monostatic Imaging Algorithms Based on Two－dimensional Principle of Stationary Phase[J].IEEE Transactions on Geoscience and Remote Sensing，2011，49（10）：3504－3520.

[11] Xiong Tao，Xing Mengdao，Wang Yong，et al.Using Derivatives of an Implicit Function to Obtain the Stationary Phase of the Two－dimension Spectrum for Bistatic SAR Imaging [J].IEEE Geoscience and Remote Sensing Letters，2011，8（6）：1165－1169.

[12] Clemente C，Soraghan J.Approximation of the Bistatic Slant Range Using Chebyshev Polynomials[J].IEEE Geoscience and Remote Sensing Letters，2012，9（4）：682－686.

[13] Rodriguez－Cassola M，Prats P，Schulze D，et al.First Bistatic Spaceborne SAR Experiments with TanDEM－X [J].IEEE Geoscience and Remote Sensing Letters，2012，9（1）：33－37.

[14] Wu Qisong，Xing Mengdao，Shi Hongzhu，et al.Exact Analytical Two－dimensional Spectrum for Bistatic Synthetic Aperture Radar in Tandem Configuration[J].IET Radar，Sonar and Navigation，2011，5（3）：349－360.

[15] 周峰.机载SAR运动补偿和窄带干扰抑制及其单通道GMTI研究[D].西安：西安电子科技大学，2007.

[16] 保铮，邢孟道，王彤.雷达成像技术 [M].北京：电子工业出版社，2005.

[17] Davidson W G，Cumming G I，Ito R M.A Chirp Scaling Approach for Processing Squint Mode SAR Data[J].IEEE Transactions on Aerospace and Electronic Systems，1996，32（1）：121－133.

[18] Raney R，Runge H，Bamler R，et al.Precision SAR Processing Using Chirp Scaling[J].IEEE Transactions on Geoscience and Remote Sensing，1994，32（4）：786－799.