半球共形阵列的两种虚拟变换方式性能对比
张学敬,杨志伟,廖桂生
(西安电子科技大学 雷 达信号处理国家重点实验室,陕西 西 安 710071)
在飞行器或其他移动平台载体表面,常常需要安装共形阵列天线[1-8].与常规均匀线阵相比,共形阵有着优越的结构特点和良好的测向性能,如其对雷达载体的空气动力学性能影响很小,且具有体积小、重量轻、易于安装等优点.此外,共形阵列能获得较大的有效孔径,在不转动阵列天线的情况下即可获得360°的覆盖范围.
由于共形阵列布阵的特殊性,导致其阵列流形不具有Vandermonde结构,使得快速子空间类算法(如root-MUSIC[9]等)不能直接应用于共形阵列,从而限制了其在工程上的应用.在非等距线阵的处理方面,文献[10]通过虚拟内插变换,将非线性阵列转换为线性阵列,并将root-MUSIC算法应用于内插变换中,实现了非线性阵列的快速波达方向估计.文献[11]提出了流形分离技术,将任意阵列的导向矢量表示成采样矩阵与具有Vandermonde结构的基矢量的乘积,其中采样矩阵描述阵列本身,基矢量反映信号的角度特征,两部分相互独立,利用基矢量的特殊结构即可实现快速波达方向估计.文献[12]将流形分离应用于稳健波束形成中.这些文献仅讨论了在特定的流形变换方式下如何对原阵列进行处理以及处理后的性能,而在不同的虚拟阵列流形选取方式对最终阵列处理性能的影响方面缺乏研究.
笔者将虚拟阵列内插方法应用于半球共形阵列中,建立了半球阵到虚拟矩形阵和虚拟十字阵的两种变换关系,并对两种方式在波达方向估计、波束形成、运算复杂度等方面的性能进行了分析对比和仿真验证.
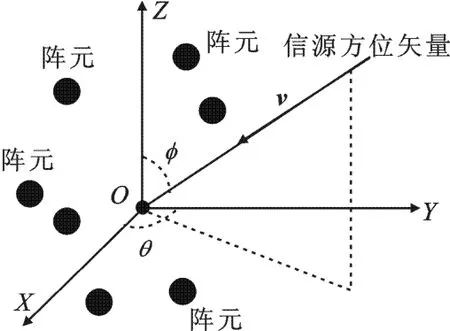
图1 任意几何结构阵列模型
1 共形阵列信号模型
对于包含N个阵元的任意几何结构阵列,建立如图1所示的正交直角坐标系O-XYZ.假设在阵列远场(θk,φk)(k=1,2,…,M)处有M 个窄带点源以平面波入射(波长为λ),其中θk为空间信源的方位角,φk为空间信源的俯仰角.阵列接收的快拍数据为

式中,X(t)为N×1快拍数据矢量,S(t)为M×1入射信号复幅度矢量,N(t)为N×1阵列噪声矢量.考虑全向一致阵元,不考虑遮挡效应,则阵列导向矢量矩阵A(θ,φ)可表示为
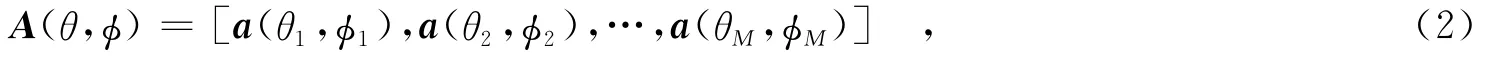
其中,a(θi,φi)为第i个信源的导向矢量.a(θi,φi)可表示为
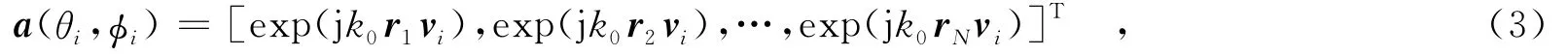
其中,k0=2πλ,为波数,其大小表示单位波长的周期数;rn=[xn,yn,zn],为第n个阵元的坐标矢量(n=1,…,N);vi= [sinφicosθi,sinφisinθi,cosφi]T,为第i个信源的空间方位矢量.
针对具体的半球共形阵列,图2给出了半球阵列的阵元分布示意图.令半球阵的第1层阵元分布在x-y平面内,每层第1个阵元位于x轴正方向,按照x-y平面内逆时针方向进行编号,则可以计算出第p层、第q个阵元的空间俯仰角φpq和空间方位角θpq,分别为

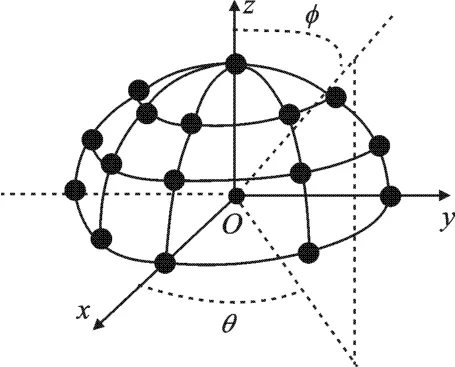
图2 半球阵列模型
式中,p=1,2,…,P,q=1,2,…,Qp,P表示阵列的层数,Qp表 示第p层的阵元个数.若设半球阵底面半径为R,则第(p,q)个阵元的位置坐标矢量为

考虑阵列远场(θ,φ)方向的某个信源,则由前可知,半球阵列的导向矢量为
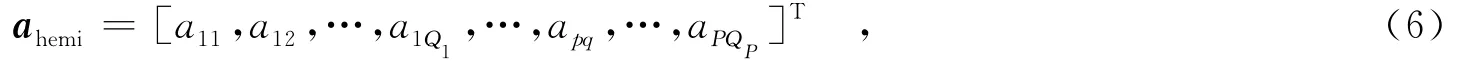
式中,apq=exp(j(2π λ )rpqv ) ,v为(θ,φ)方向的方位矢量.由此得到半球阵列的接收数据矢量为
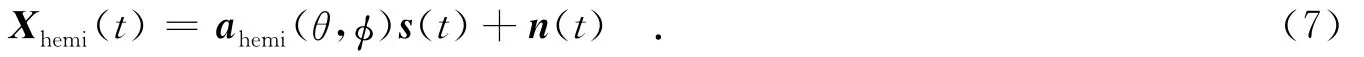
2 流形变换理论
对于非等距线阵而言,其导向矢量不具有Vandermonde结构,无法采用某些基于子空间的快速波达方向估计算法(如root-MUSIC),而直接利用MUSIC算法进行波达方向估计的运算复杂度较高.为降低运算量,可对原阵列进行流形变换,使得变换后的导向矢量满足Vandermonde或类Vandermonde结构,进而可利用新导向矢量的特殊结构来实现快速波达方向估计.
典型的流形变换方法包括流形分离类方法[11-13]和虚拟阵列变换类方法[10].流形分离方法将任意阵列的导向矢量表示成采样矩阵与具有Vandermonde结构的基矢量的乘积,通常采用傅里叶基分解或球面谐波基分解等方式来实现.对于三维阵列,由于需要两维流形分离,在阵元数较多时计算量很大,工程应用困难.虚拟阵列变换方法针对设置的虚拟阵列,采用变换矩阵将原阵列的接收数据转换为虚拟阵列的接收数据.该方法可借助虚拟阵列的特殊结构实现快速波达方向估计.
虚拟阵列变换的核心是寻找在某个角域Θl内满足a(θ)=(θ)(θ∈Θl)的变换矩阵Bl,其中a(θ)和(θ)分别表示真实阵列和虚拟阵列的导向矢量.通常要求(θ)具有Vandermonde结构.为了内容的完整性,下面仅给出求解变换矩阵的主要步骤,详细描述可参考文献[10].步骤1 将阵列的感兴趣观察区域划分为多个角域,在每个角域内取一些测试角度,例如取第l个角域
步骤2 根据真实阵列的阵元位置关系,计算第l个角域内所有测试角度对应的真实阵列导向矢量
步骤3 根据虚拟阵列的阵元位置关系,计算第l个角域内所有测试角度对应的虚拟阵列导向矢量

记真实阵列数据协方差矩阵R=ARsAH+σ2I(其中Rs为信号矢量的自协方差矩阵),则虚拟阵列数据协时虚拟阵列的信号子空间与噪声子空间不正交,所以需要进行预白化处理,变换矩阵变为

此时TlT=I成立,虚拟阵列信号子空间与噪声子空间正交.真实阵列流形与虚拟阵列流形之间的关系变为
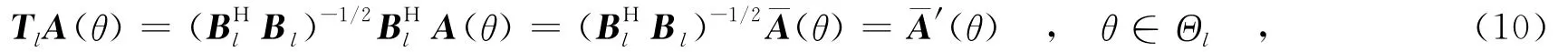
虚拟阵列的数据协方差矩阵表示为

显然,对于式(11)就可以利用基于等距线阵的各种算法进行波达方向估计,所不同的就是阵列流形,即利用上式进行波达方向估计时要注意其导向矢量是虚拟阵列的导向矢量,而不是真实阵列的导向矢量.由于虚拟阵列变换法原理简单,实现方便,计算量较小,且可以通过多种内插方式来实现,所以利用虚拟阵列内插法实现变换,并研究不同内插方式的选取对最终阵列处理性能的影响.
3 半球阵列的两种内插方式
考虑半球阵列(如图2),其阵列结构的非均匀性导致接收数据为对空间数据的非等间隔采样.为了得到等间隔采样的数据,可以采用两种均匀阵列对原阵列进行虚拟内插变换.虚拟阵列的数据相当于借助原阵列得到的对空间数据的估计,这要求其阵列设计应与原阵列在结构上具有相似性,如位置应与原阵列接近,有效孔径应与原阵列近似相等.
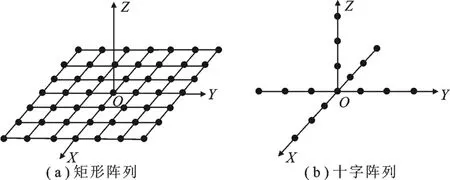
图3 虚拟阵列模型
第1种方式采用矩形阵列(如图3(a)),此时虚拟阵列在X、Y轴上与原阵列等效孔径相等,但在Z轴方向有孔径损失.第2种方式采用十字阵列(如图3(b)),此时虚拟阵列仅分布于坐标轴上,与原阵列在X、Y、Z轴上具有相同的等效孔径,这种内插方式不损失轴向孔径,同时结构较为简单.两种虚拟阵列的分布特点使得将其作为半球阵的内插阵列具有合理性.为了比较两种内插方式的性能,下面分别从转换误差[14]和孔径分布两方面对两者进行分析对比.
3.1 转换误差
转换误差的定义如下:
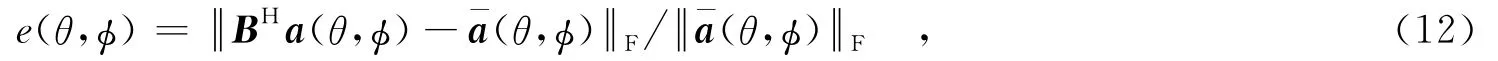

图4 转换误差
3.2 等效孔径
在等效孔径方面,分别对XOY平面孔径和Z轴孔径进行对比分析.XOY平面孔径定义为阵列在XOY平面上对信源方向的有效孔径,Z轴孔径定义为阵列在Z轴方向上对信源方向的有效孔径.分别用DXOY和DZ表示XOY平面孔径和Z 轴孔径,如图5(a)和(b)所示.
由阵列理论可知,阵列孔径越大,其分辨率越高,相应的波达方向估计性能越好,同时主瓣波束越窄.结合XOY孔径
和Z轴孔径的定义可知,两者可分别用来衡量阵列在方位维和俯仰维的波达方向估计性能以及方位维和俯仰维的主瓣宽度,阵列最终的波达方向估计性能受两种孔径综合影响.为了对比不同阵列在等效孔径方面的差异,图6给出了3种阵列的孔径随角度变化的曲线.可以看出,在XOY平面孔径方面,原半球阵列为一常数,两种虚拟阵列随方位角增大而波动变化,当方位角为45°或135°时,虚拟矩形阵列的孔径达到最大值,虚拟十字阵列的孔径取得最小值.在Z轴孔径方面,虚拟矩形阵列Z轴孔径恒为零,虚拟十字阵列与原阵列在Z轴方向的分量相同,使得两者的孔径随俯仰角变化趋势一样,均随俯仰角增大而增大.
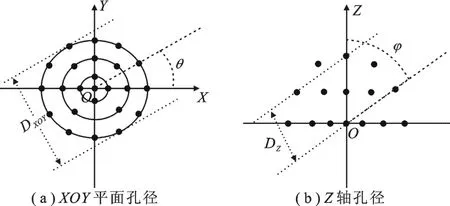
图5 等效孔径
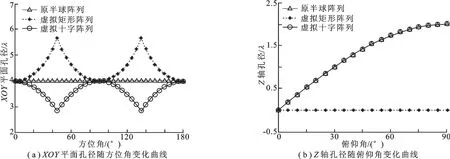
图6 孔径对比
综上可知,利用虚拟阵列进行处理,最终波达方向估计性能会受转换误差和孔径分布两种因素综合影响.可以预计:在俯仰角较大时,虽然十字阵在XOY平面的孔径较小,但它的Z轴孔径较大且转换误差小于矩形阵,波达方向估计性能优于矩形阵;在俯仰角较小时,两种虚拟阵列的转换误差和Z轴孔径均相差不大,但矩形阵在XOY平面孔径上要明显大于十字阵,此时矩形阵的波达方向估计性能较优.此外,在方位角接近45°或135°区域,矩形阵的XOY平面孔径远大于十字阵,对应的波达方向估计性能应更优.
4 运算复杂度分析
设原半球阵列的阵元数为N,若采用MUSIC算法进行二维波达方向估计,其运算复杂度主要体现在特征值分解和谱峰搜索上.根据文献[15],对维数为N×N的相关矩阵进行特征分解的运算复杂度为O[15(N-1)3].假设两维谱峰搜索的总点数为K,则谱峰搜索的运算复杂度为O[KN2].原阵列实现MUSIC算法的总的运算复杂度为O[15(N-1)3]+O[KN2].
利用虚拟阵列估计波达方向的过程可由离线运算和在线运算两步组成.离线运算主要包括计算转换矩阵B和T.考虑L个角域,则离线部分的运算复杂度为O[LN3]+O[LN¯3].在线运算主要体现在root-MUSIC算法上.对于M 元等距线阵,若采用root-MUSIC进行波达方向估计,其运算复杂度为O[120(M-1)3].笔者设虚拟阵列在X轴、Y轴上的阵元数为Nxy,同时可得虚拟十字阵列Z轴上的阵元数Nz=(Nxy+1)2,考虑到L个角域,可知虚拟矩形阵列和虚拟十字阵列进行在线波达方向估计时总的运算复杂度分别为O[240L(Nxy- 1)3]、O[255L(Nxy-1)3].由此看出,在通常情况下,虚拟矩形阵列的离线计算量大于虚拟十字阵列;若只考虑在线波达方向估计,则虚拟矩形阵列的计算量小于虚拟十字阵列.虚拟矩形阵列以大的离线计算量为代价,得到了相对较小的在线计算量.
由以上分析可知,对于三维共形阵列,在满足N≫Nxy的条件下,利用虚拟阵列实现在线波达方向估计的运算量大大降低了.
5 仿真实验
在仿真实验中,采用图2所示结构的半球共形阵列,虚拟阵列设置如图3所示.半球阵列由5个均匀分布的圆阵组合而成,各环阵元数分别为24、20、16、8、1,环与环之间服从等弧度分布,半球底面半径取2λ.虚拟矩形阵列由81个阵元构成,组成9×9方阵,阵元行列间距为λ2.虚拟十字阵列由21个阵元构成,除坐标原点阵元外,其余各阵元均匀分布于X轴、-X轴、Y轴、-Y轴、Z轴上,各轴向阵元数为4,间距为λ2.
在波达方向估计方面,对于矩形阵列,利用其结构的特殊性,在对“虚拟数据”进行行列合成处理[16]的基础上,应用2Droot-MUSIC算法[17]即可得到信源的二维波达方向估计.对于十字阵列,可利用XOY面上的十字阵列估计信源的俯仰角和方位角,利用Z轴上的等距线阵估计信源的俯仰角.为了减小估计误差,将两个俯仰角估计的均值作为最终的俯仰角估计值.
在自适应波束形成方面,将线性约束最小方差(LCMV)准则直接应用于虚拟阵列中,得到虚拟阵列的权矢量为

实验1 在上述实验参数下,分别借助虚拟矩形阵列和虚拟十字阵列进行二维波达方向估计,信噪比取0dB.经过2 000次独立的蒙特卡洛实验,得到两种内插方式进行波达方向估计的均方根误差对比结果,如图7所示.其中“圆圈”表示十字阵列的均方根误差小于矩形阵列的均方根误差,“星号”与之相反.
可以看出,两种内插方式的波达方向估计性能受信源俯仰角的影响较大.当俯仰角较小时,矩形阵内插的性能较优;随着俯仰角的增加,十字阵估计性能逐渐优于矩形阵的估计性能.另外,两者的性能对比结果关于90°方位角对称.当信源方位角靠近45°(或135°)时,矩形阵列的波达方向估计性能较优,与理论预测一致.
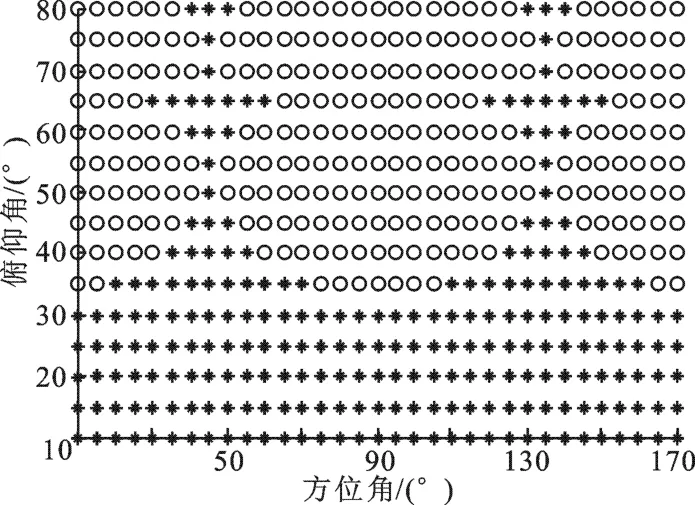
图7 两种内插方式的波达方向估计性能对比
实验2 分别将信源方向固定为(45°,30°)和(90°,50°),信噪比从-15dB增至15dB,经过2 000次独立的蒙特卡洛实验,得到这两个角度下两种虚拟内插方式进行波达方向估计以及直接利用原阵列MUSIC算法进行波达方向估计的性能变化对比曲线,如图8所示.
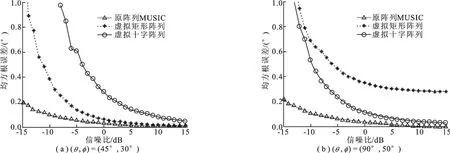
图8 3种阵列波达方向估计性能随信噪比变化曲线
可以看出,两种虚拟内插方式在信噪比较小时波达方向估计性能较差;随着信噪比的增大,两者的估计性能逐渐变优,虚拟十字阵列变化趋势明显,而虚拟矩形阵列变化趋势较为平坦.与原阵列MUSIC算法相比,虚拟阵列的波达方向估计性能略差.
实验3 设来波方向(θ,φ)=(120°,30°),干扰方向(θ,φ)=(30°,60°),信噪比为0dB,干信比为10dB,快拍次数取为1 000,分别在原阵列、矩形虚拟阵列、十字虚拟阵列上利用线性约束最小方差准则,得到3种阵列的三维方向图,如图9所示.图10对比了3种阵列构型在主瓣方向的方位维方向图和俯仰维方向图.图11对比了3种阵列构型在干扰方向的方位维方向图和俯仰维方向图.表1为
3个方向图在方位维和俯仰维的主瓣宽度对比.
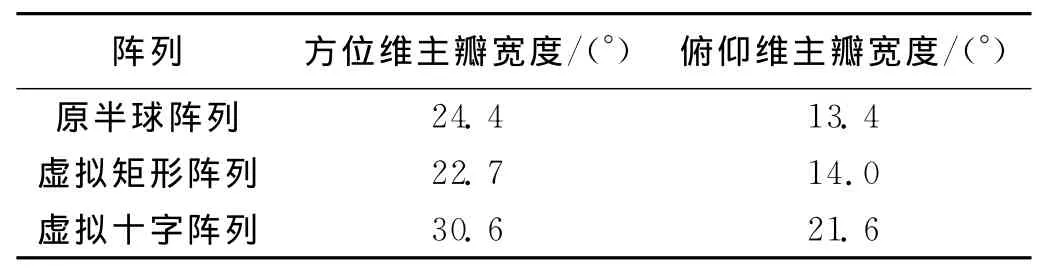
表1 阵列主瓣宽度对比

图9 三维方向图
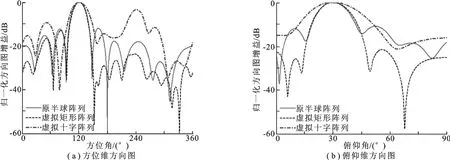
图10 主瓣方向剖面图
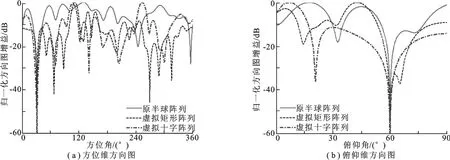
图11 干扰方向剖面图
可以看出,两种虚拟阵列均可以在期望方向形成主瓣的同时对干扰进行抑制.在两维主瓣宽度上,虚拟矩形阵列在方位维的主瓣宽度比原阵列的窄,在俯仰维的主瓣宽度比原阵列的宽,整体与原半球阵列接近.虚拟十字阵列在两维主瓣宽度上都宽于原阵列.在干扰方向图上,具有较窄主瓣宽度的方向图其在干扰方向的凹口也较窄,即凹口相对宽度与主瓣相对宽度保持一致.另外,不难看出,阵列方向图宽度对比与各阵列孔径分布特点(图6所示)相一致.
实验4 将输入信噪比从-20dB增至20dB,其余参数同实验3,得到3种阵列构型方向图的输出信干噪比(SINR)随输入信噪比变化的曲线,如图12所示.
可以看出,3种阵列输出信干噪比均随着输入信噪比的增大而增大.在相同输入信噪比下,3种阵列的输出信干噪比由大到小依次为虚拟矩形阵列、原阵列、虚拟十字阵列,可知3种阵列按抗干扰能力强弱排布依次为虚拟矩形阵列、原阵列、虚拟十字阵列.这是因为与原半球阵列相比,虚拟矩形阵列阵元数较多,增加了系统自由度,使得其在满足特定约束自由度的条件下拥有更多的自适应自由度来抑制干扰和噪声,所以输出信干噪比大于原阵列.同理,虚拟十字阵列与原阵列相比,减少了系统自由度,其自适应自由度降低,相当于对原阵列进行降秩处理,此时的波束形成性能(即输出信干噪比)显然会下降.
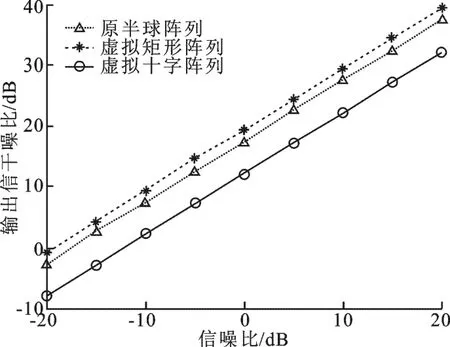
图12 阵列输出信干噪比随输入信噪比变化的曲线
6 总 结
笔者将虚拟内插变换的思想应用于半球共形阵列中,分别建立了半球共形阵列到矩形阵列和十字阵列的两种变换关系,并利用虚拟阵列进行波达方向估计、波束形成等阵列处理.对两种内插方式在波达方向估计、波束形成、运算复杂度等方面进行了全面分析和仿真验证,可为共形阵列的工程应用提供参考.文中的分析和仿真虽然是在半球阵下进行的,但虚拟阵列变换方法的适用性却不会受到阵列排布的制约,这是因为如果原共形阵列满足空间无模糊采样条件,那么总是可以通过合适的转换矩阵将其内插为均匀线阵/面阵或两者的组合.同时,文中所描述的虚拟内插变换的性能分析方法对于一般共形阵列仍然适用,这也扩大了笔者提出方法的适用范围.另外,文中阵列均是在理想情况下进行分析和仿真的,当阵列存在误差时如何进行虚拟内插还需进一步探讨和研究.
[1] Josefsson L,Patrik P.Conformal Array Antenna Theory and Design[M].New Jersey:IEEE Press,2006.
[2] Bai Y Y,Xiao S,Liu C,et al.A Hybrid IWO/PSO Algorithm for Pattern Synthesis of Conformal Phased Arrays[J].IEEE Transactions on Antennas and Propagation,2013,61(4):2328-2332.
[3] Blomberg A E A,Austeng A,Hansen R E.Adaptive Beamforming Applied to a Cylindrical Sonar Array Using an Interpolated Array Transformation[J].IEEE Journal of Oceanic Engineering,2012,37(1):25-34.
[4] Karimzadeh R,Hakkak M,Haddadi A,et al.Conformal Array Pattern Synthesis Using the Weighted Alternating Reverse Projection Method Considering Mutual Coupling and Embedded-element Pattern Effects[J].IET Microwaves,Antennas &Propagation,2012,6(6):621-626.
[5] Zou L,Lasenby J,He Z.Direction and Polarisation Estimation Using Polarised Cylindrical Conformal Arrays[J].IET Signal Processing,2012,6(5):395-403.
[6] Costa M,Richter A,Koivunen V.DoA and Polarization Estimation for Arbitrary Array Configurations[J].IEEE Transactions on Signal Processing,2012,60(5):2330-2343.
[7] 张凡,张福顺,赵钢,等.共形天线阵列方向图分析与综合[J].西安电子科技大学学报,2010,37(3):496-501.Zhang Fan,Zhang Fushun,Zhao Gang,et al.Pattern Analysis and Synthesis of the Conformal Antennas Array[J].Journal of Xidian University,2010,37(3):496-501.
[8] 王布宏,郭英,王永良,等.共形天线阵列流形的建模方法[J].电子学报,2009,37(3):481-484.Wang Buhong,Guo Ying,Wang Yongliang,et al.Array Manifold Modeling for Conformal Array Antenna[J].Acta Electronica Sinica,2009,37(3):481-484.
[9] Barabell A J.Improving the Resolution Performance of Eigenstructure-based Direction-finding Algorithms[C]//Proceedings of the International Conference on Acoustics,Speech and Signal Processing.New York:IEEE,1983:336-339.
[10] Friedlander B.The Root-MUSIC Algorithm for Direction Finding with Interpolated Arrays[J].Signal Processing,1993,30(1):15-29.
[11] Belloni F,Richter A,Koivunen V.DoA Estimation Via Manifold Separation for Arbitrary Array Structures[J].IEEE Transactions on Signal Processing,2007,55(10):4800-4810.
[12] Yang P,Yang F,Nie Z P,et al.Robust Beamformer Using Manifold Separation Technique for Semispherical Conformal Array[J].IEEE Antennas and Wireless Propagation Letters,2011,10:1035-1038.
[13] Costa M,Richter A,Koivunen V.Unified Array Manifold Decomposition Based on Spherical Harmonics and 2-D Fourier Basis[J].IEEE Transactions on Signal Processing,2010,58(9):4634-4645.
[14] 王永良,陈辉.空间谱估计理论与算法[M].北京:清华大学出版社,2004.
[15] Golub G H.Matrix Computations[M].Baltimore:Johns Hopkins University Press,1984.
[16] Chen Y M.On Spatial Smoothing for Two-dimensional Direction-of-arrival Estimation of Coherent Signals[J].IEEE Transactions on Signal Processing,1997,45(7):1689-1696.
[17] Wong K T,Zoltowski M D.Root-MUSIC-based Azimuth-elevation Angle-of-arrival Estimation with Uniformly Spaced But Arbitrarily Oriented Velocity Hydrophones[J].IEEE Transactions on Signal Processing,1999,47(12):3250-3260.

