相空间混沌扩频通信及其误码率

吴成茂，李杜娟

（西安邮电大学 电子工程学院，陕西 西安710121）

随着通信技术的快速发展，扩频通信现已具有较强的抗干扰、抗噪声、抗多径衰落等性能特性，在军事通信中不仅发挥出了不可替代的作用，同时在民用和商用通信的各个方面也有了广泛地渗透，如卫星通信、移动通信、微波通信、全球个人通信、蜂窝系统、无线定位系统、无线局域网等［1］。扩频通信，其传输速率不仅较高，而且其传输的可靠性和安全性能也得到了较大改善。近年来，在扩频通信理论研究中，信号调制方式［2］、扩频增益［3］、干扰方式［4］，以及信噪比［1］等对扩频通 信误码率的影响，已被学者们进行了探讨，并将采用误码率作为衡量扩频系统性能指标的重要依据，以此来解决信道干扰、多径信号引起的衰落，以及通信安全等重要问题。但是扩频通信系统还尚有一些不足，由于信号之间非正交性且相似，易与其他设备间产生相互干扰，使得通信系统通信效率降低且传输的可靠性变差，以致通信系统质量受到影响。为了解决扩频通信中存在的以上问题，文献［5－7］提出了采用混沌映射产生扩频码实现直扩通信，但不同类型的混沌信号所产生混沌序列［8］性能具有较为明显的差异。因此，寻找适合扩频通信的混沌信号成为当前混沌通信中的热点问题，也正是本文所要探究的问题所在。通过测试经典Logistic映射所产生混沌序列和相空间混沌序列作为扩频码应用于扩频通信系统的误码率，对比分析误码率与相应序列间的统计相关特性，并揭示二者之间的关联性，为扩频通信系统寻找较低误码率的扩频码产生方式。

1 相空间混沌扩频通信系统

为了使得扩频通信系统的通信质量有所提高，拟将在扩频通信系统中引入不同相空间混沌信号，其中相空间混沌扩频通信的原理如图1所示。

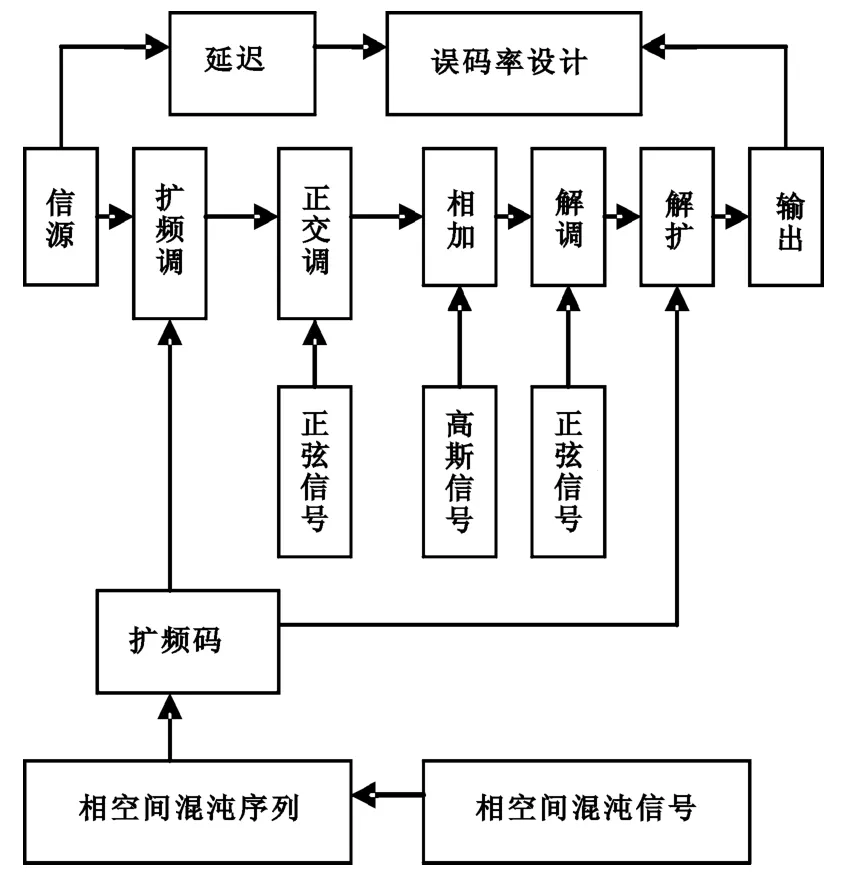
图1 相空间混沌扩频通信系统

2 混沌序列的产生方式

扩频码作为扩频通信的关键，其产生方式不同，使得扩频通信系统的性能将会有所差异。经典Logistic映射及其利用相空间法改良混沌序列产生扩频码的基本原理如下。

2.1 Logistic映射

Logistic映射具有良好的混沌特性，在混沌保密通信的很多领域都被广泛应用。Logistic映射表达式为［9］

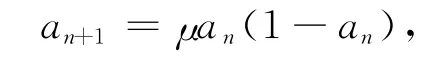
其中μ为控制参数，a1为初始条件。若该映射的控制参数满足

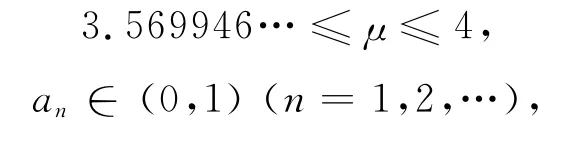
则Logistic映射处于混沌状态。当μ＝4时，Logistic映射为满射。

2.2 相空间混沌信号

混沌信号具有良好的初值敏感性和相关特性等性能，近年来被作为扩频序列产生研究的重要方法。

文献 ［10］提出了 Autocorrelation of Phasespace Axial Symmetric（APAS）定理，对于一个平稳遍历的离散实动力系统

其值域为［－a，a］，a为正实数；｛x（n）｝的均值为0，且取值的正负具有统计平衡性。

相空间混沌信号分为低维混沌信号、高维混沌信号和空时混沌信号3种。

（1）低维混沌信号

在低维混沌信号中，以改良Henon序列为例来对其特性作说明，其动力方程为［10］

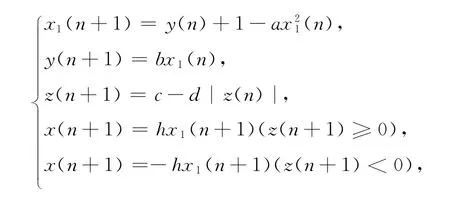
其中x（n）∈ ℝ 是状态变量；a，b，c，d，h是系统参数，且为正数。

（2）高维混沌信号

在高维混沌信号中，其序列在多个方向上都具有扩张性。选取CML序列作对称性改良，其动力方程为［10］

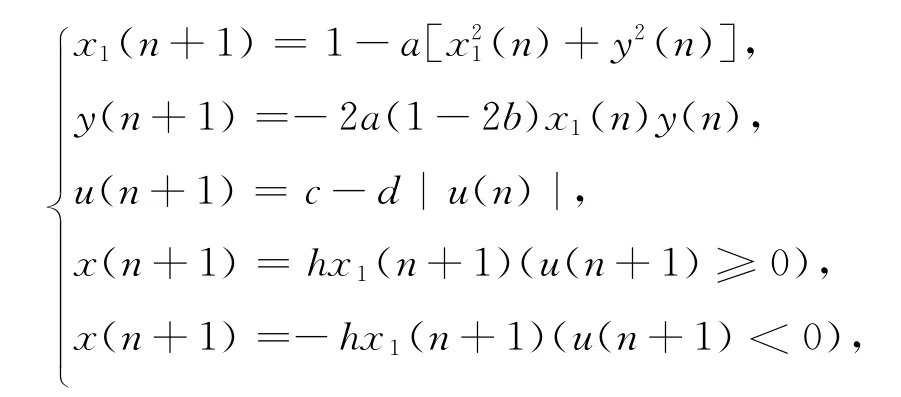
其中x（n）∈ ℝ 是状态变量；a，b，c，d，h是系统参数，且为正数。

（3）空时混沌信号

所谓空时混沌系统，就是序列在空间和时间上的演化都有耦合性，并且该行为表现出了极大的复杂性，现如今已有了广泛应用。因此，利用空时混沌系统来改良基于Logistic映射的OCML序列，其动力方程为［10］

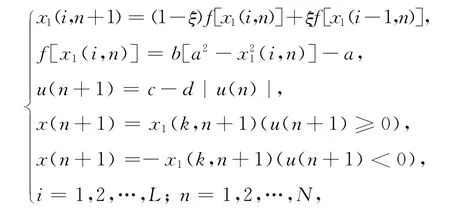
其中x（i，n）∈ ℝ 是状态变量；f（x）是Logistic映射；a，b，c，d，ξ，k是系统参数；L 是空时系统的尺度；N是序列的长度。

3 混沌序列性能分析

混沌序列性能指标是衡量混沌信号性能好坏的重要指标，对扩频通信系统的性能有着重要影响。因此，对以下混沌信号的指标性能进行测试分析。

3.1 李雅普诺夫指数

n维系统的Lyapunov指数定义式为［10］

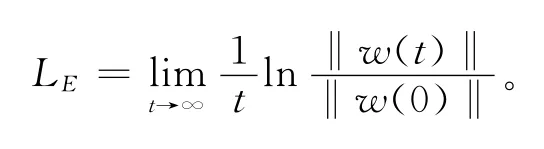
在Matlab下，对经典Logistic映射及其利用相空间法改良后混沌序列的Lyapunov指数进行仿真测试，所得结果分别如图2和图3所示。

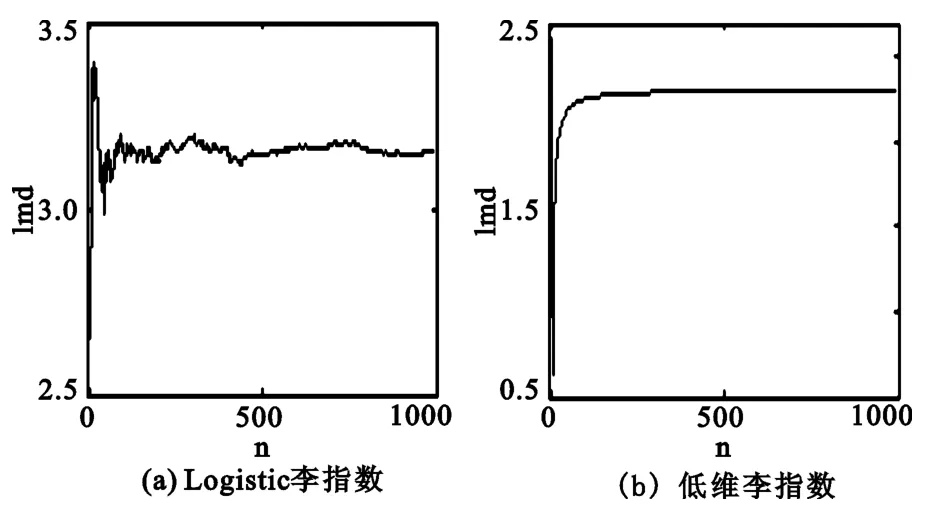
图2 Logistic和低维混沌序列Lyapunov指数

图3 高维和空时混沌序列Lyapunov指数

将上述不同扩频序列的最大Lyapunov指数测试结果进行比较，详细结果如表1所示。

表1 最大Lyapunov指数仿真测试结果

3.2 相关性

对于扩频序列，设｛ai｝与｛bi｝是周期为N的两个码序列，即

码字｛ai｝与｛bi｝的互相关函数Rab（τ）定义为［11］

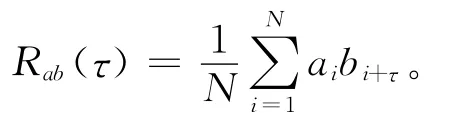
若Rab（τ）＝0，则｛ai｝与｛bi｝正交。

长度为N的码序列｛ai｝的自相关函数Ra（τ）定义为［11］

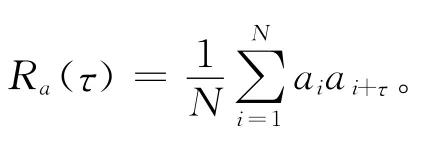
在Matlab下，对经典Logistic映射及其利用相空间法改良后混沌序列的相关特性进行仿真测试，所得结果分别如图4至图7所示。

图4 Logistic混沌序列相关性

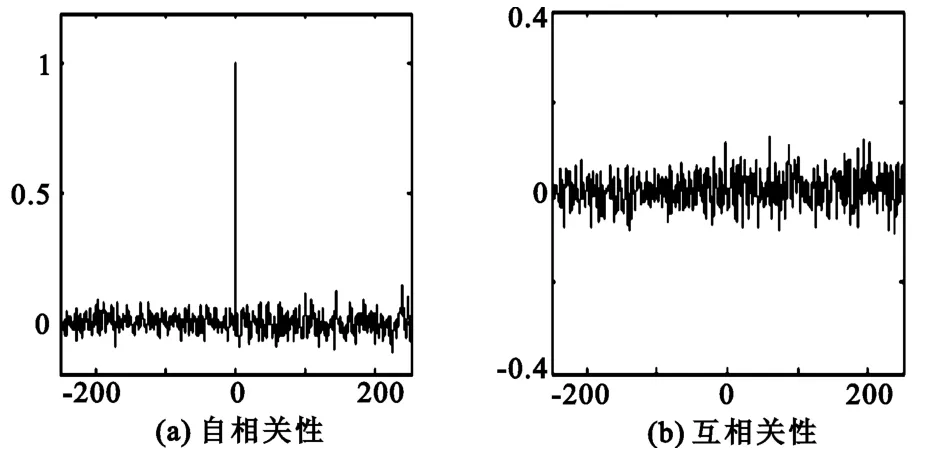
图5 低维混沌序列相关性

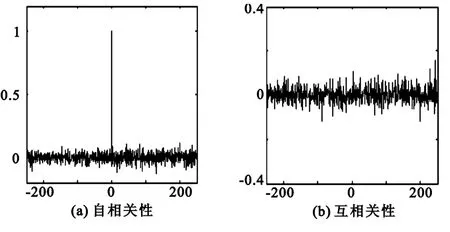
图6 高维混沌序列相关性

图7 空时混沌序列相关性

将上述不同类型混沌序列的相关性曲线测试结果进行比较和分析，其详细结果如表2所示。

表2 不同混沌序列的相关性比较

3.3 均值和方差

概率论中，均值和方差是用来描述随机变量分布特点的两种最常用的数字特征。

均值反映了随机变量平均取值的大小，其定义式为［12］

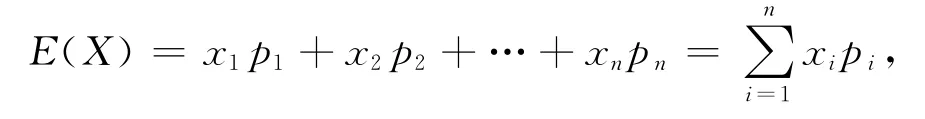
其中E（X）是均值，pi为不同情况下的随机变量X对应的概率。

方差是用来度量随机变量和均值之间的偏离程度，其计算公式定义为

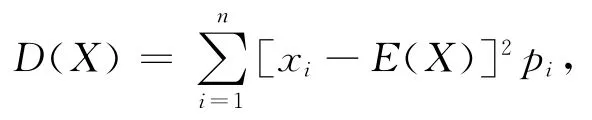
其中D（X）为方差，E（X）和pi分别为随机变量X对应的均值和X＝xi的概率。

为了对混沌序列的互相关性作进一步的定量分析，在仿真测试经典Logistic映射和利用相空间法改良混沌信号所产生的混沌序列互相关特性时，对其描述互相关特性曲线特征的均值和方差也进行了测试，其测试结果如表3所示。

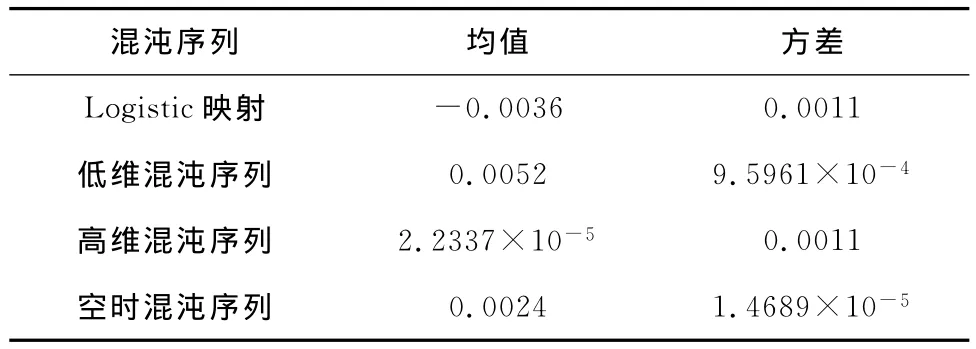
表3 混沌序列互相关性曲线的均值和方差

4 扩频系统的误码率

将不同混沌序列作为扩频码应用于扩频通信系统中，并对其误码率进行测试。

4.1 扩频通信系统的误码率

误码率作为衡量通信系统可靠性的一个重要指标，其计算方法依据柯捷尔尼科夫理论可知，扩频通信系统误码率的表达式为

其中F为信号的频率，E为信号能量；N0为噪声功率谱密度。而在实际的相空间混沌扩频通信中，其误码率的计算可采用

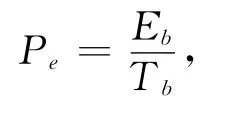
其中信号传输中出现错误的比特数为Eb，总的传输信号的比特数为Tb。

在实验仿真测试中，所采用的测试条件和测试方法参照文［13］所述，此处不再赘述。

4.2 相空间扩频码误码率测试分析

在混沌扩频通信中，将不同混沌序列作为扩频码应用于扩频通信系统中，其误码率结果如表4所示。

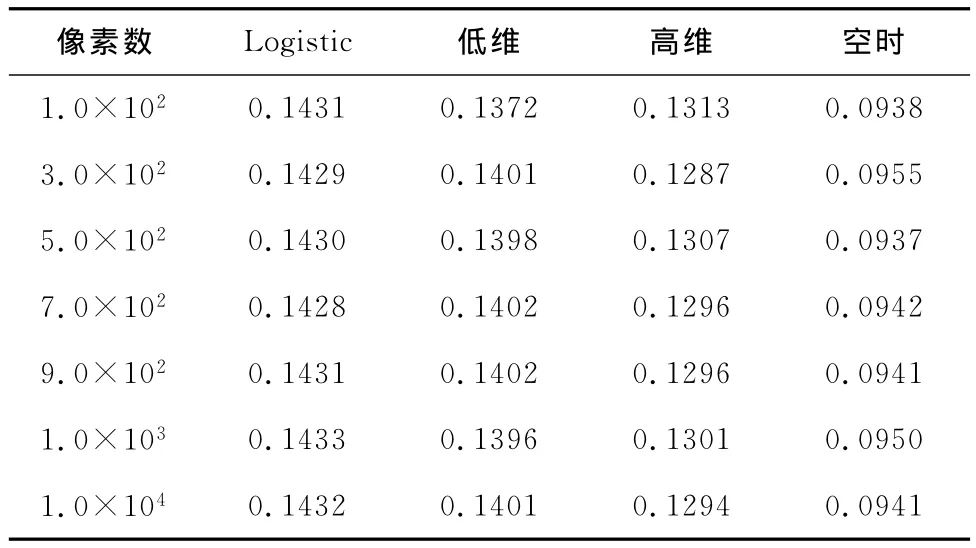
表4 不同混沌序列在不同像素下的误码率

由表4可知，经典Logistic映射所产生混沌序列的误码率平均值约为0.143；利用相空间法改良混沌序列，采用低维混沌序列作为扩频码的误码率平均值约为0.139，采用高维混沌序列作为扩频码的误码率平均值约为0.130，采用空时混沌序列作为扩频码的误码率平均值约为0.094。表明Logistic混沌序列误码率性能相对最差，改良后的空时混沌序列的误码率性能相对最好。其原因在于改良后的空时混沌序列的自相关性和互相关性相比都非常好，而经典Logistic映射产生混沌序列的自相关性和互相关性都是较好，相比其他相空间混沌序列的相关特性较差（见表2）。相比而言，利用相空间法改良低维混沌序列比经典Logistic映射产生混沌序列的误码率降低了0.004，高维混沌序列比经典Logistic混沌序列的误码率降低了0.013，空时混沌序列比经典Logistic混沌序列的误码率降低了0.049。显然，空时混沌序列的误码率相对减少的最多，其值为4.9%。原因在于利用相空间法改良后的空时混沌序列所对应的自相关和互相关特性都相比最好，因此，所对应的误码率更低是合理的，保证了信号传输的准确率，有利于扩频通信系统的需要。

通过将表2中的扩频码序列的统计相关特性与表4中所对应的误码率作对照，结果发现扩频码序列的统计相关特性与其相应误码率的大小之间存在很大的关联性。相比统计互相关特性，扩频码的统计自相关特性对扩频系统误码率的影响颇为明显。而对于统计自相关特性相同的两个扩频序列，其统计互相关特性相对较好的扩频序列所对应的误码率将会更低。

5 结论

通过仿真实验，对经典Logistic映射所产生混沌序列和利用相空间法改良后混沌序列作为扩频码的误码率进行了测试，结果表明扩频码的误码率大小与其相应的统计相关特性之间有密切联系。实验发现，利用相空间法改良后的空时混沌序列作扩频码，能够相对较好的降低扩频系统的误码率，保证信号传输的准确率，提高了扩频系统的安全性，有利于扩频通信需要。

［1］黄乘顺，李星亮.基于混沌的扩频通信系统及性能分析［J］.通信技术，2008，41（12）：37－39.

［2］张蕾，郑实勤.基于MATLAB的直接序列扩频通信系统性能仿真分析研究［J］.电气传动自动化，2007，29（3）：39－42.

［3］王亥，胡健东.数字混沌扩频通信系统［J］.北京邮电大学学报，1998，21（4）：7－11.

［4］曾璐，谢晓尧.基于MATLAB扩频通信系统误码率的研究［J］.通信技术，2011，44（11）：25－29.

［5］张怡，费恒敏，赵恒斌，等.混沌序列相关特性研究及在扩频通信中的应用［J］.火力与指挥控制，2011，36（11）：18－24.

［6］刘利，张建东，郑志军.混沌扩频通信系统仿真［J］.舰船电子工程，2010，196（10）：75－103.

［7］田东，何世彪，郑鹏宇.基于数字混沌编码器的扩频通信研究［J］.数字通信，2012，7（1）：29－36.

［8］刘雪松，李立萍.混沌扩频通信系统及其干扰技术研究［D］.成都：电子科技大学，2009：22－24.

［9］范九伦，张雪峰.分段Logistic混沌映射及其性能分析［J］.电子学报，2009，29（7）：720－725.

［10］陈滨，周正欧.混沌波形的相关性［M］.西安：西安电子科技大学出版社，2011：13－136.

［11］田日才.扩频通信［M］.北京：清华大学出版社，2007：61－62.

［12］盛骤，谢式千，潘承毅.概率论与数理统计［M］.3版.北京：高等教育出版社，2001，68－156.

［13］吴成茂，李杜娟，王保平.混沌扩频通信及其误码率［J］.西安邮电大学学报，2013，18（3）：10－13.