切线法数控成形非球面机床的定位误差补偿研究
于 博, 于正林, 顾莉栋, 周家贺, 曲超平
(长春理工大学,吉林长春 130022)
切线法数控成形非球面机床的定位误差补偿研究
于 博, 于正林, 顾莉栋, 周家贺, 曲超平
(长春理工大学,吉林长春 130022)
针对自主研发的切线法数控成形非球面机床,提出一种基于改进型PID控制算法结合开发型UMAC软件定位误差补偿方法,给出了具体实现步骤。通过建立改进型PID控制模型和开发型UMAC误差修正表对切线法数控成形非球面机床进行定位误差补偿,实际应用和实验验证表明,该方法可以有效地解决数控机床的定位误差问题。
计量学;定位误差补偿;切线法;数控机床
1 引 言
数控机床(CNC)的进给系统是实现超精密加工的关键,也是系统误差进行动态、静态补偿的关键。其系统由直线电机本体、直线电机驱动器、UMAC(Universal Motion and Automation Controller)和位置检测单元组成。直线电机与传统的旋转电机相比,简化了传动机构、摩擦小、无齿隙误差、响应速度快,因此,将直线电机应用于精密数控机床实现零件加工的微进给已成为当前趋势[1~3]。但是,由于直线电机通常直接连接于负载,使得其对负载变化和外部扰动变得敏感,直接影响进给系统的定位精度,所以要实现该类进给系统的高精度伺服控制,必须采取有效的控制措施。
数控机床进给系统的定位精度是影响其加工精度的关键因素[4,5]。为了提高切线法数控成形非球面机床的加工精度,首要解决的问题是提高该进给系统的定位精度。本课题以UMAC为硬件控制平台,针对机床控制原理提出采用前馈PID控制器实现伺服控制;对UMAC硬件单元开发了软件补偿功能,对机床进行定位误差补偿,实验结果表明该定位误差补偿方法可有效地提高数控机床的定位精度。
2 改进型PID控制
2.1 总体控制
切线法数控成形非球面机床采用双闭环控制系统[6,7]。由于该机床以速度插补原理为控制核心[8,9],传统的单一型位置环控制系统已不适用,故采用了综合型速度环控制系统。通常控制器闭合速度环不受量化误差和数字速度采样频率的限制,才能使系统获得较高的速度环增益、刚性和抗干扰能力。但是,绝大部分速度环的刚性来自速度积分增益,积分增益会导致系统响应外部指令产生延迟,因此,采用闭合速度环的控制器不适用于追求快速启停的控制系统中[10,11]。所以本机床控制系统选取UMAC的位置环作为控制外环,速度环作为控制内环,在控制器参数调整过程中重点关注速度稳定性,以速度曲线为调控对象,通过试凑调整控制器参数来提高数控机床的控制精度。
2.2 改进型PID控制算法
PID控制器产生作用的前提条件是被控量与设定值之间必须存在一个偏差,系统通过识别偏差才能实现控制,而简单的PID控制器会使控制系统产生滞后现象。精密数控机床的伺服控制系统对跟踪精度要求很高,伺服系统输入是已知的时变进给信号,要求被控对象以零稳态误差跟踪和响应系统输入信号,因此,简单的PID控制器不能满足上述要求。加拿大学者Yusuf Altintas通过对数控机床位置伺服的建模分析,证明了伺服控制的开环增益与系统跟随误差成反比关系,即增大开环增益可减小跟随误差,但是驱动系统的机械惯量、电机力矩和放大器限制了开环增益的过大,而采用前馈PID控制是解决上述问题有效方法[12]。
图1为带前馈的复合控制结构简图,其中R(s)、C(s)分别为系统输入和输出函数;E(s)为系统误差函数;G(s)为PID控制器传递函数;Gp(s)为被控对象传递函数;F(s)为前馈环节传递函数。
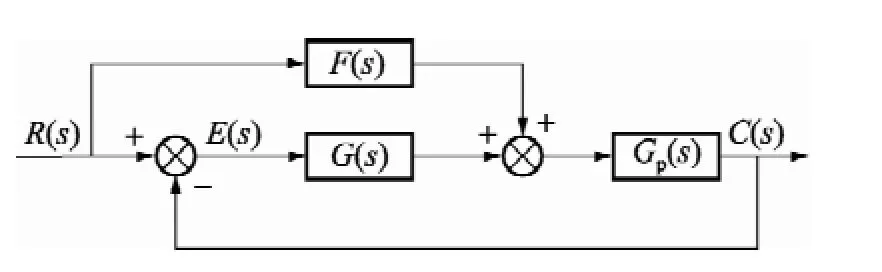
图1 带前馈的复合控制结构
由图1可推导出,带前馈系统的误差传递函数为:
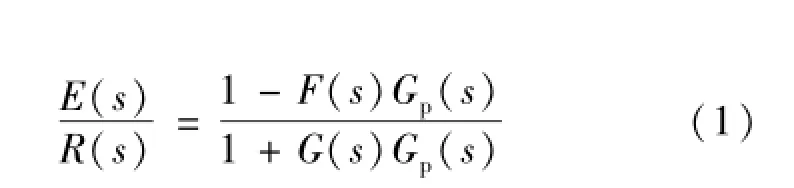
无前馈的传递函数为:

式(1)说明,当前馈函数满足F(s)=Gp(s)-1时,误差传递函数为0,即C(s)=R(s)。此时输出完全再现输入,即无论输入信号怎样变化,系统误差始终为0。式(1)与式(2)相比较可知,带前馈的控制系统与原控制系统特征方程一样,这说明前馈补偿没有影响原系统的稳定性。因此,这种前馈控制理论上可认为是一种理想的控制方式,但是实际应用中想完全实现该控制是不现实的,其原因是:(1)任何系统的线性范围都是有限的;(2)高阶微分装置设计难度大,而且对噪声较敏感,同时微分阶数过高也会影响系统的干扰抑制性能。通常前馈控制的微分阶数为2阶时才可获得满意效果。
图2所示为改进型前馈PID控制器结构图,其中r(t)、y(t)分别为系统输入和输出函数;Kaff为加速度前馈增益量值;Kvff为速度前馈增益量值;KI为积分增益量值;KD为微分增益量值。
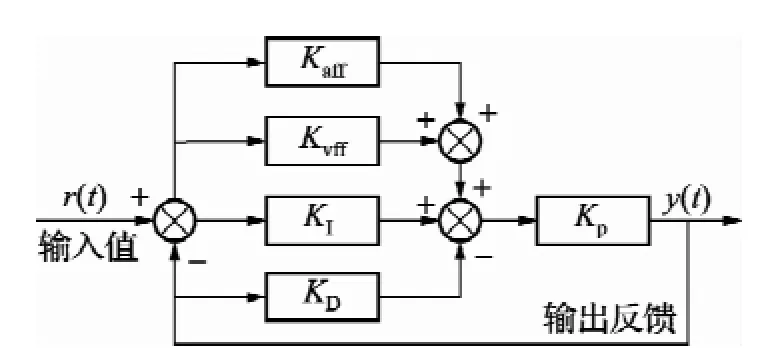
图2 改进型前馈PID控制器结构
综上所述,引入1阶速度前馈和2阶加速度前馈到PID控制器中,可减小系统的跟随误差。将该控制器应用于切线法数控成形非球面机床,可以提高伺服系统跟踪精度,进而改善进给系统的定位精度。
3 开发型UMAC软件补偿
3.1 定位误差的测量
机床定位精度是指运动部件在进给系统的作用下所能达到的位置精度[13]。定位误差的大小一般可以采用激光干涉仪、光栅尺、刻线基准尺、读数显微镜和感应同步器等测量得到。
本文采用英国雷尼绍公司ML-10型双频激光干涉仪分别对该机床X轴运动方向进行定位误差检测。图3所示为该机床的定位精度检测图。
为了消除随机误差对轴向定位精度的影响,本文采用多次测量取平均值法得到定位误差。测量时,分别以10 mm、20 mm为移动步长,重复测量5次(Xstroke:±100 mm),计算平均值得定位误差。

图3 定位精度检测图
3.2 开发型UMAC软件补偿
与传统控制器不同,UMAC控制器具有螺旋补偿、间隙补偿和力矩补偿等功能,根据提供的补偿功能可在任意伺服周期内对被控对象实施定位补偿。为系统添加一个特定的修正变量,使其与原有误差大小相等、方向相反。补偿后节点定位误差为:
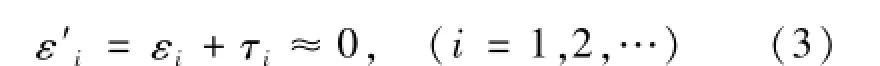
式中,εi为补偿前节点的定位误差值;τi为误差修正值。
开发型UMAC软件补偿的实现步骤:1)通过实际测量得到节点累积误差表或误差曲线;2)通过计算得到误差修正值并转换成误差修正表;3)通过定义补偿表及相关参数使误差修正表生效。进给系统执行程序时,UMAC自动读取误差修正表,根据电机实际位置在表内找到对应修正值,如果没有对应值就在相邻点间利用插值法得到修正值,从而实现进给系统的定位补偿。
设置误差修正表时应注意:1)在设置节点误差修正值时,其值的1/16是脉冲单位,且必须是整数;2)误差修正值应与实际误差值符号相反;3)在电机绝对零点处的误差修正值应设置为0。
4 实验分析
按照上述方法对“切线法数控成形非球面机床”的X轴方向进行了定位补偿实验。
(1)实验室环境条件
温度20±0.5℃;湿度32.54%RH;压强1 007.20×102Pa。
(2)进给机构的运动描述
从绝对零点正方向以10 mm(ε1)、20 mm(ε2)为步长运行,直到正极限为止,之后回到绝对零点,再以相同步长向反方向运行,直至负极限为止,以上过程往复运行5次,且运行过程中在各节点处均停留4 s,以便于双频激光干涉仪采集数据。
表1为该机床X轴运动方向补偿前后的定位误差值。
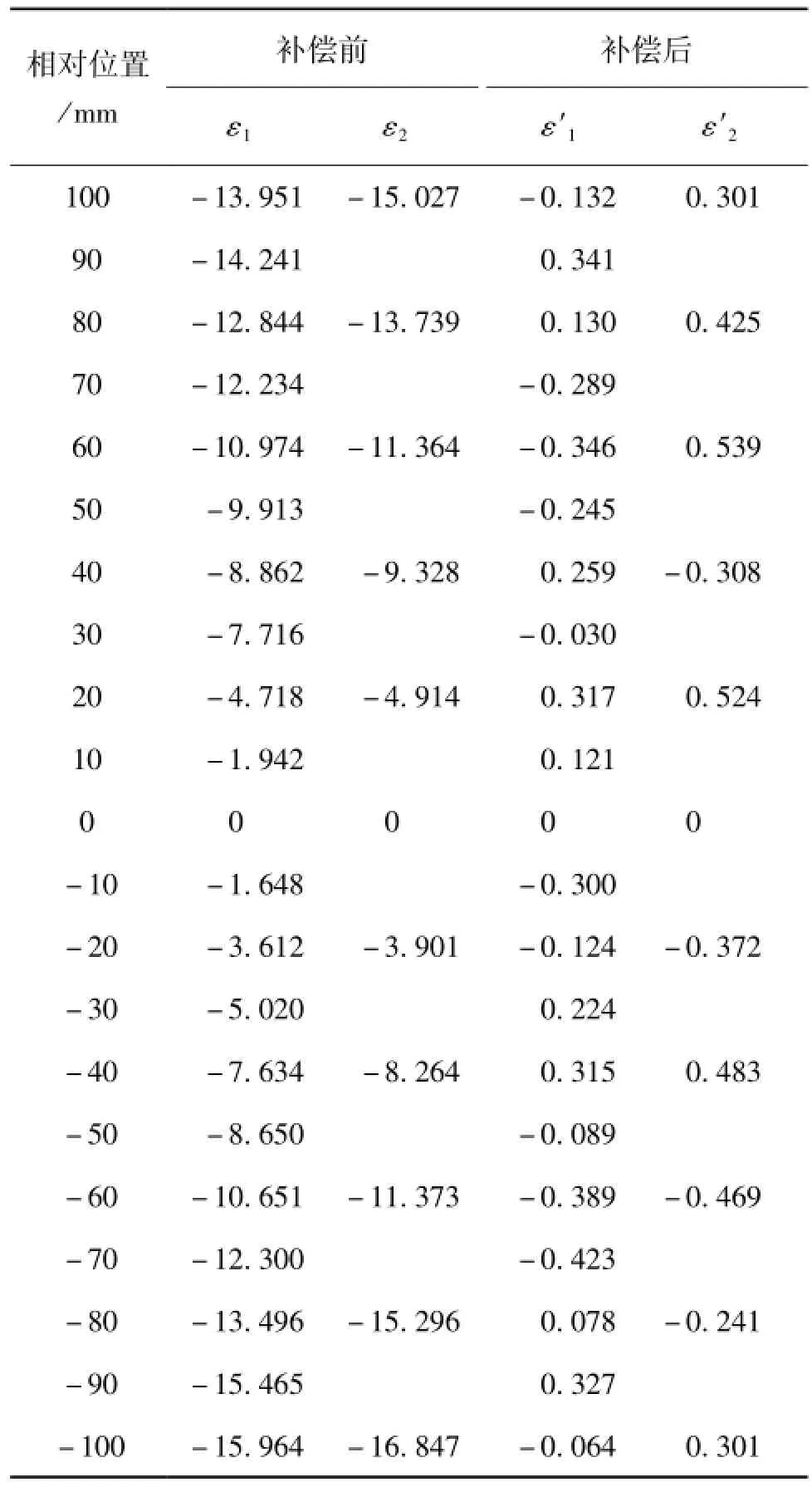
表1 机床X轴补偿前后定位误差μm
对表1进行分析后得出:
(1)定位误差既有累积性,也有一定非线性,且定位误差随位移的增加而增加,在不同的位置段,对应的定位误差值各不相同。
(2)补偿后定位误差值与补偿前相比,节点误差大幅减小,且整体数据得到明显改善。
(3)补偿效果比较。相比ε′2值,ε′1的补偿后误差值更为理想,且经计算ε′1的方差更小,说明移动步长的距离大小直接决定补偿效果的优劣。
从而可以看出:基于改进型PID控制算法结合开发型UMAC软件定位误差补偿法是一种非常有效的方法。
5 结 论
利用改进型PID控制算法和开发型UMAC软件补偿对切线法数控成形非球面机床实施定位误差补偿,有效地降低了机床的定位误差。该补偿方法简单、明确、通用性强、不受机床的结构和运动复杂程度的限制,而且对于提高现有数控机床的定位精度以及提升普通型数控机床的精密量级均有借鉴意义。
[1] 王先逵,陈定积,吴丹.机床进给系统用直线电动机综述[J].制造技术与机床,2001,(8):18-21.
[2] 张春良,陈子辰,梅德庆.直线驱动新技术及其在加工装备上的应用[J].电工技术学报,2002,17(5):45-49.
[3] 蔡长春,徐志峰,潘晶,等.直线电机的发展和应用[J].微电机,2003,36(2):47-50.
[4] 王哲,赵爱国,赵德云,等.数控机床定位精度的综合分析[J].机械设计与制造,2010,(9):132-133.
[5] 周汉辉.数控机床精度校准技术[J].计量技术,2006,(2):27-29.
[6] 张珂,吴玉厚.椭圆零件精密加工中直线电机的控制与应用[J].航空制造技术,2004.(3):33-35.
[7] 吴玉厚,潘振宁.PMAC控制器中PID调节的应用[J].沈阳建筑工程学院学报,2004.20(2):20-21.
[8] 朴成稿,于化东,顾莉栋,等.切线法数控加工高次非球面新原理的提出[J].吉林大学学报,2011,41(7):134-239.
[9] 于化东,顾莉栋,朴成稿,等.用切线法速控加工高次非球面[J].吉林大学学报,2012,42(2):354-359.
[10] 陶永华.新型PID控制及其应用[M].北京:机械工业出版社,2005.
[11] 孙洪程,李大宇,翁维勤.过程控制工程[M].北京:高等教育出版社,2006.
[12] Yusuf Altintas.数控技术与制造自动化[M].北京:化学工业出版社,2002.
[13] 邓朝晖,周红利,万琳琳.数控机床定位精度的研究[J].制造技术与机床,2008.(6):107-110.
The Location Error Compensate of Aspheric CNC by Tangent Method
YU Bo, YU Zheng-lin, GU Li-dong, ZHOU Jia-he, QU Chao-ping
(Changchun University of Science and Technology,Changchun,Jilin 130022,China)
Based on feed-forward PID algorithm and UMAC software,a compensate location errormethed is proposed for the aspheric CNC by tangentmethod which was developed by ourselves,and specific steps to implement thismethod is given.The experimental results of location error compensation showed this method can improve the location accuracy of CNC effectively by the established feed-forward PID model and an UMAC error correct table.
Metrology;Location error compensate;Tangentmethlod;CNC
TP92
A
1000-1158(2014)06-0555-04
10.3969/j.issn.1000-1158.2014.06.07
2013-06-21;
2014-07-03
国家自然科学基金(50775014)
于博(1987-),男,黑龙江佳木斯人,长春理工大学博士研究生,主要研究方向为机电系统控制理论与技术研究. yubo745@163.com

