可动屏蔽型计算电容复现电容单位的方法研究

陆祖良，黄璐，杨雁，赵建亭，钱进，陆文骏，刘忠有，张钟华， 刘秀英， 王建波， 王 维， 何小兵

（1.中国计量科学研究院，北京 100029； 2.同济大学物理科学与工程学院，上海 200092）

可动屏蔽型计算电容复现电容单位的方法研究

陆祖良1，黄璐1，杨雁1，赵建亭1，钱进1，陆文骏1，刘忠有1，张钟华1， 刘秀英1， 王建波2， 王 维1， 何小兵1

（1.中国计量科学研究院，北京 100029； 2.同济大学物理科学与工程学院，上海 200092）

中国计量科学研究院建立了标准不确定度为2×10－8的可动屏蔽型计算电容装置。该装置复现电容单位量值只与屏蔽电极所移动的轴向长度有关。采用激光干涉仪测量这个长度时，一般无法提供干涉条纹数。经典方法采用替换方法，逐步从已知的小整数扩大到大整数。过程复杂，所需条件多。提出了一种新的复现电容单位的方法。对应复现电容量值的干涉条纹整数由一个准确度等级相对较低的仪器直接确定。其干涉条纹小数则通过电容电桥的两次平衡确定。所需结构及过程简单，操作方便。给出了该方法的详细内容及其优点，报告了检查装置线性的实验及其结果。

计量学；计算电容；国际单位制；复现单位；基准

1 引 言

计算电容在原理上只需要一维长度的测量即可，因而容易获得较高的准确度［1］。自上世纪50年代以来，计算电容作为阻抗基准，不仅提高了电容、电感、交流电阻的测量水平（在当时计算电感10－5的测量水平上获得了2至3个数量级的提高），结合直流量子化霍尔电阻准确测量精细结构常数，而且推动了感应分压器、交流电桥等新技术的迅速发展，极大地促进了电磁计量的发展。目前，计算电容是除量子电压和量子电阻之外电磁计量领域内准确度水平最高的计量基准装置（10－8）［2～9］。

近年来，澳大利亚计量院（NMIA）与国际计量局（BIPM）合作建立新的可动屏蔽型计算电容装置［10，11］，加拿大计量院（NRC）、中国计量科学研究院（NIM）也参加了这个合作。美国标准技术研究院（NIST）结合光梳测长新技术，开展了新型计算电容的研究［12］。

中国计量科学研究院在“十一五”国家科技支撑计划项目“以量子物理为基础的现代计量基准研究”中，设立“精细结构常数测量关键技术及电容基准的研究”课题，开展了可动屏蔽型计算电容的研究，包括计算电容本体、电容电桥、电容电阻电桥、激光测长等方面的内容。至2013年12月，完成了课题规定的任务。复现1 pF固定标准电容器单位的标准不确定度达到2.0×10－8，并测量了精细结构常数［13］。

可动屏蔽型计算电容是通过激光在两个位置上的实时测长，克服移动电极端部效应的影响，从而获得较为准确的值。其特点是电容单位的复现过程，是从先后两次测量中获得一个结果。NMIA的W.K.Clothier在当时的情况下，设计了一套完整的复现方法［14］。但该方法需要一系列条件的保证。本课题组结合现有条件，提出了一个改进方法，具有过程简单、对器件要求不高、操作方便等优点。本文报告这个改进方法，并作一般性讨论。

2 典型复现方法回顾

2.1 可动屏蔽型计算电容的原理

由4个绝缘小间隙分开的4个无穷长导电柱面形成的二维场，相对的两个电容在单位长度上的平均值近似为一个常数C0＝（εrε0／π）ln 2。因此，只需要测量轴向长度即可确定电容量值。我国上世纪70年代建立的卧式刻线型计算电容［15～18］，其轴向长度由激光干涉仪先行测量确定。但是一旦安装之后，使用中可能的变化很难用再次测量轴向长度的办法来解决。这种技术方案一般达到10－7水平。

可动屏蔽型计算电容则采用另外的技术方案，立式的4根电极之间上下各安装一个屏蔽电极，其中一个先后移动到两个位置，与另外一个固定的屏蔽电极产生两个电容。它们之间的差克服了屏蔽电极端部对二维场的影响。但仍残存部分影响。国外一般采用机械补偿的方法，补偿后达到10－8水平；我国则提出了电补偿的方法［19，20］，具有调节方便、补偿分辨率高等优点；模型试验验证了电补偿法比机械补偿法有一个多数量级的优势［21］，将在后续研究中应用。

2.2 可动屏蔽型计算电容复现电容单位的经典方法

卧式刻线型计算电容的轴向长度由两端的刻线决定，其长度在安装前先行测量，由激光干涉仪给出。在可动屏蔽型计算电容中，激光干涉仪安装在计算电容装置内部，以满足实时测量的需要。此时如果要求激光测长过程中给出整数条纹，必将增加装置的复杂性，增加技术难度。一般不这样做。文献［14］给出的一个经典方法简述如下。

所述装置使用的激光波长为546.227 05 nm，半波长对应的电容值为0.533 540×10－6pF。W.K.Clothier称之为“条纹单位”（fringe unit），记为fu。实质上是一个干涉条纹的电容当量，本文称之为“条纹当量”。装置的自动控制系统使可动屏蔽电极锁定在干涉条纹的整数倍上。这样，所复现的计算电容值CS呈现为fu，2fu，3fu，…这种量子化的形式。当电容电桥比较计算电容CS和未知的固定电容CX时，实际上是确定比值CX／CS（或者CX／fu）的准确数值。

2.2.1 小数部分确定

该方法在电容电桥中设计了一个绕组，与一个6盘的变压器Tr连接，将一个可调小值固定电容器连接在这个变压器Tr上，见图1。通过可动屏蔽电极在小范围内的可控移动，与这个变压器Tr相比较。由此在电桥中提供一个条纹当量的可调节量，其量程为1 000个条纹，分辨率为0.001个条纹（实际达到0.01个条纹）。量值复现中的条纹小数部分由变压器Tr提供。

2.2.2 整数部分确定

该装置复现的电容量值为0.25 pF。制造4个量值分别为0.002 pF、0.01 pF、0.05 pF和0.25 pF的固定电容器。首先确定0.002 pF对应的条纹整数。理论上0.002 pF相当于3 748.54fu；将上述1 000个条纹的量程扩大到4 000个条纹，通过一个特定的过程，把条纹整数准确记录在0.002 pF上。然后用0.01 pF将记录条纹整数扩大5倍。继续进行这样的过程，通过0.05 pF和0.25 pF，最后记录在0.25 pF上的条纹整数为468 567个。其中第一步测量0.002 pF电容器的条纹整数，变压器Tr量程由1 000扩大到4000个条纹，是通过附加的变压器翻倍实现的。而条纹整数从0.002 pF扩大5倍到0.01 pF的详细过程，简介如下。

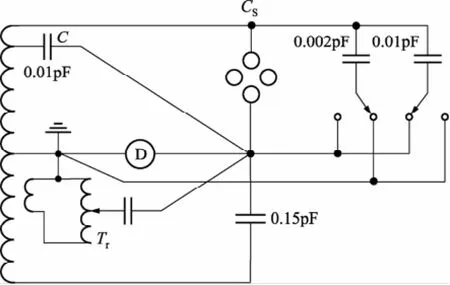
图1 扩展条纹整数示意图

1）将电桥上臂的计算电容CS与0.01 pF并联，与下臂的0.15 pF平衡，调节CS可动屏蔽电极位置（第一个位置），并记录变压器Tr读数；

2）保持CS不变，将0.01 pF接到电桥主绕组的80%接头处，将0.002 pF（已经知道它的条纹整数）与CS并联，再次平衡；

3）拿掉0.002 pF，而将CS可动屏蔽电极移动到新的位置（第二个位置），使电桥平衡，由此，CS新位置所移动的轴向长度与0.002 pF的整数条纹个数相当，或者说，将0.002 pF保存的整数条纹个数转移到CS上了；

4）将0.002 pF重新与CS并联，而将0.01 pF接到主绕组的60%接头处，电桥平衡；再拿掉0.002 pF，再次移动可动屏蔽电极到又一个新的位置，由此把0.002 pF的条纹整数的两倍转移到CS上了；

5）继续这样的过程，一直到把0.002 pF条纹整数的5倍转移到CS上；

6）通过电桥平衡，把CS保存的整数转移到0.01 pF上。

最终的0.25 pF，正是该计算电容装置所设计复现的量值。上述整个过程只在装置建立的开始阶段一次性进行（称为build-up）。日常测量0.25 pF固定电容器时，条纹的整数部分使用保存值，仅仅测量条纹的小数部分。

这个方法没有对激光干涉仪提出实时提供整数条纹个数的要求。整个过程尽管复杂，在当时的条件之下是必要的。这个过程体现了计算电容装置的自我完备性。

上述简单介绍中，可以看到过程需要的几个条件：

具有一定稳定性的4个小电容器，其量值与条纹整数倍接近；

具有一定稳定性的几个辅助的电容器（0.01 pF、0.15 pF等）；

光、机、电3个部分在全量程范围内具备必要的线性；

电桥多次平衡，累加效应要求电桥本身具备一定的稳定度；

电桥主绕组的几个接头处（100%，80%，60%，40%，20%）轮换接入不同大小的电容器，在高准确度要求下（例如10－8）其负载效应将产生影响，为克服这个影响，需要记录不同负载情况下电桥比率绕组的比差和角差，因此将大幅度增加校准工作量。

3 一种新的量值复现方法

3.1 基本情况

本课题主电极由316号无磁不锈钢制造，直径50 mm，长度470 mm，在中间370 mm的有效长度上，平均不圆柱度不超过±25 nm。复现的电容量值为0.4 pF，由可动屏蔽电极的两个位置（对应电容0.6 pF和0.2 pF）得到。采用633 nm兰姆凹陷He-Ne激光，将其锁定在半波长整数倍上［22］。为了获得更低的不确定度，引入633 nm碘稳频He-Ne激光波长标准对兰姆凹陷He-Ne激光的波长（频率）做实时校准。名义波长对应的条纹当量为fu＝0.618 789 872×10－6pF。

3.2 电容电桥

所设计的电容电桥采用二端对导纳方式，如图2所示。计算电容CS接在电桥的端钮“10”上，被测电容CX（1 pF）接在端钮“4”上，过渡电容CF（6 pF）接在端钮“－1”上。补偿电势连接在过渡电容CF所在桥臂上。电桥平衡时，由补偿电势给出比差和角差的读数α和β。

电桥采用了一种自动辅助平衡方法，提高了测量速度。并采用新的完全等电位屏蔽校验方法，在工作状态下校验感应分压器（IVD），校验不确定度减低至10－9水平［23］。

3.3 新的整数和小数确定方法

3.3.1 电桥两次平衡确定的关系式

在图2所示的桥路中，当移动电极处于Ctop＝0.6 pF位置时，可以写出以下的平衡关系式：

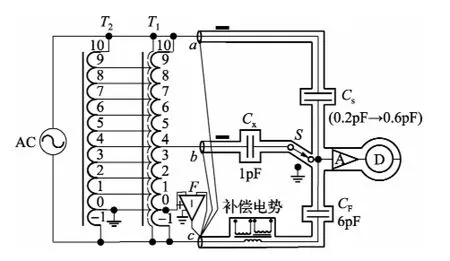
图2 电容电桥示意图

根据目前的设计和安装调整，在差值（Ctop－Cbottom）中，端部效应和接近效应在10－10水平上可以忽略。该差值为条纹当量的整数倍。

式中，n1和n2分别是在两个锁定位置时干涉条纹的总数，两者均为整数。

由于标准电容器损耗（角差）很小，不影响电容的测量，所以在只考虑电容的模而不考虑角差时，式（3）可以写为

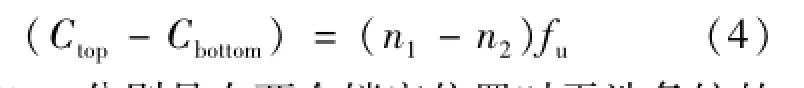
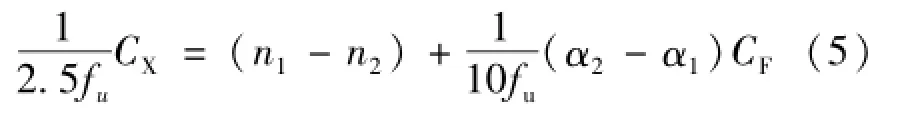
式（5）是一个被测量CX的条纹数关系式，其单位是无量纲的。如果CX的干涉条纹数被求出，那么很容易转换成以pF为单位表达的数值。CX的干涉条纹数，由式（5）右边的两项表示，第一项是整数，第二项中有小数也可能有整数。因此CX的干涉条纹数的小数部分仅由第二项决定，整数部分则两项共同决定。根据这个分析，可以在不必具体知道n1和n2的情况下，计算CX的干涉条纹数。

3.3.2 整数部分确定

CX的干涉条纹数的整数部分可由其他过程得到，例如从中国计量科学研究院原有的计算电容基准（卧式刻线型）测量得到。

从式（5）可以知道条纹整数1对应于2.5fu。为了获得准确的整数部分，测量CX仪器的分辨率应达到0.5个条纹，对应于1.25fu，在633 nm的激光条件下，1.25fu≈0.77×10－6pF。因此对于CX＝1 pF而言，为了得到准确的整数部分，其测量仪器本身准确度应达到0.77×10－6。中国计量科学研究院原有的计算电容装置满足这个要求。

如果CX能保持长期稳定性不低于0.77×10－6（这不是一个很高的要求），那么上述测量只要在开始时进行一次即可。

3.3.3 小数部分确定

在这一项中，10fu≈6.18×10－6pF，CF为6 pF；电桥读数（α2－α1）／10－6一般小于100。如果需要小数部分有3位小数准确可靠，那么需要CF值的前面5位有效数字是准确的（CF前面两位可能被（α2－α1）／10－6变成整数）。这是一个并不困难的要求，通过商用数字电容电桥AH2700A就可达到。

假如第二项计算得到的是正数，如3.643 5，那么直接用这个小数0.6435即可；假如计算得到的是负数，那么用这个小数的余数。如计算得到－1.356 7，所要的小数则是0.643 3。

把整数部分和小数部分合起来，再乘以2.5fu就是所要的CX。

3.3.4 方法的非线性

当式（5）右边第二项所表示的小数从零逐渐增加，到达1.000时，则又回到了零（0.000）。因此尽管这种变化在局部是线性的，但在整体上，该方法是非线性的，并呈现一种周期性的变化。图3表示1 pF条纹小数随电桥读数差（α2－α1）／10－6变化的部分情况。

从图3中可以看出，对于确定的条纹小数，例如0.423，相应的电桥读数差可以有多个，见表1。

1pF电容器条纹整数为646 946。按照原理，测量时可动屏蔽电极应该在规定的两个位置上，两者相差646 946个条纹。表1的数据表明，在实际测量时，在规定的位置附近，上下几个条纹的偏离是允许的，0.6 pF和0.2 pF两个位置都可以有少量的偏离。这一点大大方便了操作，而且不会引起粗大误差。

表1的数据还表明，当可动屏蔽电极产生1个条纹的移动时，电桥读数应有1.030×10－6的响应。实际装置中，这个系数的稳定性取决于光、机、电的线性。

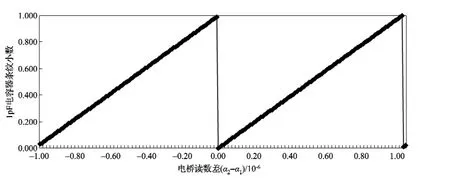
图3 电容器1 pF条纹小数随电桥读数差（α2－α1）／10－6的变化

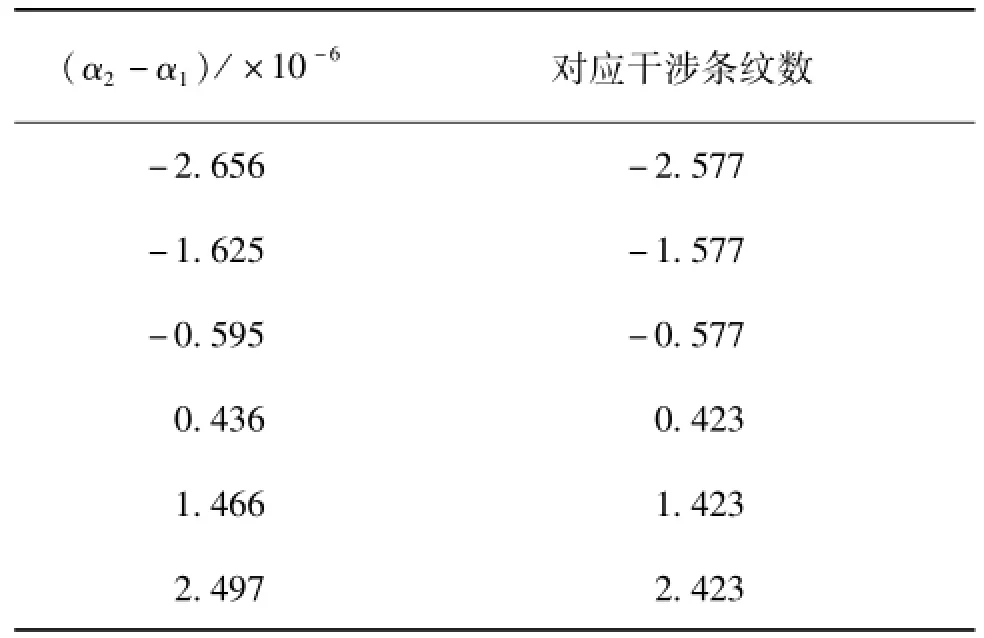
表1 当1 pF电容器条纹小数0.423时，理论上可能的电桥读数差

这里获得的系数1.030×10－6直接用于实际测量，而没有调整到如［14］中的1.00×10－6，由此保证了电桥本身的简洁。

正由于这是一个非线性的方法，我们在实验中经常采用多次测量求平均的运算，只能针对最后的电容值进行，不能对电桥读数（α1和α2）进行。

装置中采用碘稳频He-Ne激光器做实时校准，相对不确定度达10－9数量级。由此可能引起上下两个位置上的波长值的不同，这与式（5）中的假定不符合。为此，实际测量中对式（5）的形式进行了相应的修正。

3.4 与经典方法的比较

本文方法与经典方法［14］比较，都需要确定条纹的整数和小数。但从单位复现的角度看，两者的区别是明显的。本文方法基于一个较低等级的基准，一步确定了条纹整数。除了被测电容器1 pF和过渡电容6 pF外，不需要其他的电容器。对电容电桥的结构也没有提出特别的要求，只是与读数相关的补偿电势应连接在CF所在桥臂上，否则得不到式（5）这样的关系。电桥操作非常简便。首先不需要开始阶段的多次替换测量；其次在正常的测量中，对屏蔽电极的位置要求不高。对两个固定电容器1 pF和6 pF没有特别严格的要求。它们分别安置在控温箱之中，没有安装在电桥线路内部，对它们的稳定性监视十分方便。经典方法中要求多个小电容器接入电容电桥的不同接头处，产生的负载效应将使电桥的校准过程非常复杂。本文方法避免了这个缺点。

本文方法的缺点是需要其他测量仪器的一次性支持。

4 线性实验

从表1得出，1个条纹对应于电桥读数为1.030 ×10－6，这个系数也可从式（5）得出。

由于大范围内的条纹个数不可能知道，因而大范围内的线性原则上不可能测量。而局部移动条纹是可控的，因此局部的线性是可以测量的。

其实，在某些条件下，大范围的问题可以转化为局部的变化。假如测量α2时的位置不变，而α1在其设定位置附近测量两次，两次之间稍有移动。这时大范围的变化为（α2－α12）－（α2－α11）＝（－α12＋α11），等式右边就是α1附近的局部变化。所以在一个位置情况不变的条件下，大范围内的线性可以转化为另外一个位置附近的局部线性。以下通过0.6 pF和0.2 pF两个位置附近的局部移动实验，有条件地验证这个系数，检查装置总体的线性。

在0.6 pF和0.2 pF位置附近分别移动可动屏蔽电极，增加和减少几个条纹的轴向长度，结合电桥读数，计算上述系数。实验结果如表2和表3所示。

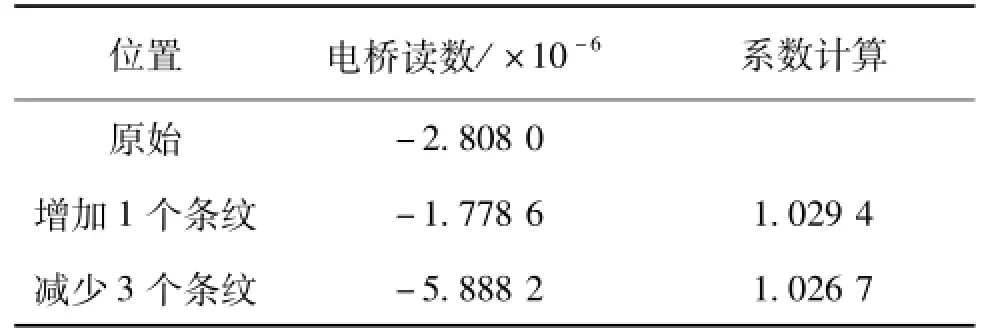
表2 位于0.2 pF附近的线性考察

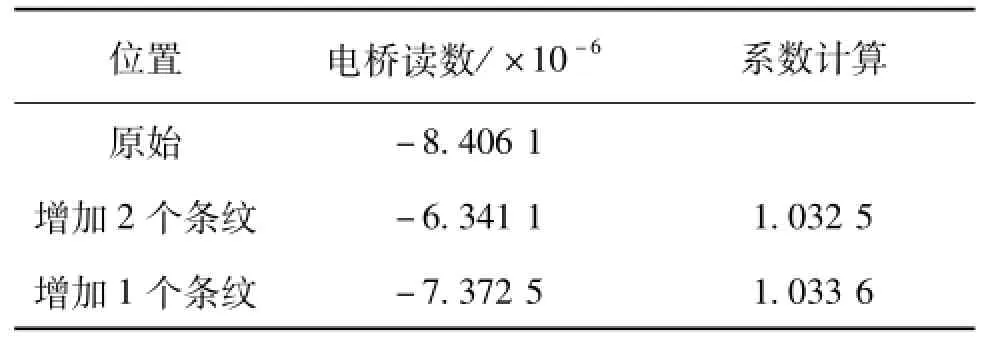
表3 位于0.6 pF附近的线性考察

两个表的数据表明，所检查的线性与准确值1.030相比，误差均在10－9量级。

多次复现1 pF固定电容器的实验标准偏差小于1×10－8。这个标准偏差中包括了大范围内的线性，也含有其他的因素。由此可推断，大范围内线性小于1×10－8，或大范围内线性的误差也在10－9量级。

5 讨 论

本文的方法需要用其它的仪器测量1 pF电容器，对这种仪器准确性要求达到0.77×10－6（与所采用的激光波长有关，并非固定不变）。利用原有的卧式刻线型计算电容基准装置，完全满足所提的要求。

其实在一个基准的基础上发展出新的基准，是计量基准研究中经常采用的方法。

例如，1 000 kV工频电压基准建立在500 kV电压基准的基础上［24］；感应分流器在高准确度水平上实现了1∶2的分流比例，3个这样的感应分流器串联，实现了1∶8的分流比例［25］；从10 kHz以下电容基准赋值的特制电容器，经过高频扫描，测量其内部阻抗参数随频率的变化，可以扩频建立至1 MHz下的电容基准［26］；文献［27］研制了4个高准确度的直流电流比较仪，工作电流较大的直流电流比较仪由较小的直流电流基准传递，最终达到了5 kA的工作电流。上述（电压）量程、（电流）比例、（电容）频率、（直流电流比较仪）工作电流，都属于计量特性。这些例子表明，在原有计量基准的基础上，扩展其计量特性而成为新的计量基准，是一个常用的方法。本文提出的方法，选择对不确定度进行了扩展。具体而言，从已有卧式刻线型计算电容基准的10－7水平扩展到了新基准的10－8水平。

本文提出的新方法，利用了现有的技术基础，收到了简单方便的效果。但在不具备较高准确度仪器的条件下，原则上不能直接使用本方法。在此情况下，基准的自身完备性研究仍然是必要的。

条纹当量fu是一个微观意义上的电容，它与宏观电容之间有一个确切的整数倍关系。这个大数的确定就是从微观向宏观过渡的过程。应用激光干涉仪测量长度的一般方法中应有其相应大数确定方法。在电容测量领域，文献［14］和本文的两种方法是激光测长一般方法的补充，它们可以相互验证。

另外还可以有其他的方法，例如以直流电阻基准为起点，通过交直流差可计算电阻—电容电阻电桥—电容这条线路也可以达到确定条纹整数的目的。

6 结 论

计算电容目前仍然是除量子电压和量子电阻之外电磁计量领域内准确度最高的基准装置。本文回顾了经典的单位量值复现方法。这是一个完备的过程，但也存在过程复杂、要求辅助条件多等缺点。在已有技术条件的基础上，本文提出了一个新的方法。将待测电容器的干涉条纹整数由一个准确度等级较低的仪器测量直接确定。至于该电容器的干涉条纹小数，则通过电桥的两次平衡完成。线性实验结果表明，在线性10－9水平上，可动屏蔽电极的两个位置不需要严格限定。该方法过程简单，操作方便。在原有基准上扩展计量特性而得到更高水平的新基准。这里采用了这个基准研究中常用的方法，对不确定度这个计量特性的扩展进行了尝试。

致谢：本文所提方法询问了澳大利亚计量院的Greig Small先生，感谢他的支持。

［1］ Thompson A M，Lampard D G.A New Theorem in Electrostatics and its Application to Calculable Standardsof Capacitance［J］.Nature，1956，177（4515）：888.

［2］ Cutkosky R D.New NBSMeasurements of the Absolute Farad and Ohm［J］.IEEE Transactions on Instrumentation and Measurement，1974，23（4）：305－309.

［3］ Rayner G H.NPL Calculable Capacitor［J］.IEEE Transactions on Instrumentation and Measurement，1972，21（4）：361－365.

［4］ Bachmair H，Fleischer H，Fleischhauer K，et al. Determination of the SIUnit Ohm Based on a Calculable Cross Capacitor［J］.Metrologia，1986，22：223－225.

［5］ Trapon G，Thévenot O，Lacueille JC，et al.Progress in linking the Farad and the RK value to the SI units at BNM-LCIE［J］.IEEE Transactions on Instrumentation and Measurement，2001，50（2）：572－575.

［6］ Clothier W K.A Calculable Standard of Capacitance［J］．Metrologia，1964，1：36－55.

［7］ Small GW，Ricketts BW，Coogan PC.A Reevaluation of the NML Absolute Ohm and Quantized Hall Resistance Determinations［J］.IEEE Transactionson Instrumentation and Measurement，1989，38（5）：245－248.

［8］ Wood B.The NRC Calculable Capacitor and Its Role in the SI［C］／／NCSL International Workshop and Symposium，2006

［9］ Igarashi T，Koizumi Y，Kanno M.Determination of an Absolute Capacitance by a Horizontal Cross Capacitor［J］.IEEE Transactions on Instrumentation and Measurement，1968，17（4）：226－231.

［10］ Small G W.Fabrication of the Main electrodes of the NMIA-BIPM Calculable Capacitor［C］／／CPEM 2010 Digest，Daejeon，Korea，2010，543－544.

［11］ Small GW，Fiander JR.Design of a Calculable Cross-Capacitor［C］／／CPEM 2004 Digest，London，2004，485－486.

［12］ Yicheng Wang，Rae Duk Lee，Liang Lu，etal.Nextgeneration calculable capacitor using a tunable-laser interferometer［C］／／CPEM 2008 Digest，Broom field，2008，686－687.

［13］ 陆祖良，等.精细结构常数测量关键技术及电容基准的研究［R］.中国计量科学研究院，2014.

［14］ Clothier W K.A Calculable Standard of Capacitance［C］／／National Standards Laboratory Division of Applied Physics，Sydney，1963.

［15］ Zhang Zhonghua.A Cross-Capacitor with fixed value in NIM［J］.ACTAMetrologica Sinica，1985，6（1）：33－38.

［16］ 何朝来，阮永顺，金士杰，等.电阻、电容、电感的绝对测量（计算电容法）［J］.电测与仪表，1979，19（9）：1－10.

［17］ 金士杰，何朝来，陆文骏，等.计算电容与电学阻抗的绝对测量［J］.计量学报，1980，1（1）：16－26.

［18］ 陆文骏.电感测量和使用中的几个问题［C］／／电磁测量文集，第二次全国电磁计量与精密测试学术交流会，中国计量测试学会，福州，1981，147－151.

［19］ Zhang Zhonghua，Lu Zuliang.A New Method for Reducing the End-Effect Error of the Cross-Capacitor with a Movable Guard Rod［J］.ACTA Metrologica Sinica，1982，3（4）：250－258.

［20］ 陆祖良.可动屏蔽型计算电容端部效应的研究及降低端部效应误差的一个新方案［D］.北京：中国计量科学研究院，1981.

［21］ Huang Lu，Small GW，Lu Zuliang，et al.Model tests of electrical compensationmethod for the new calculable cross-capacitor at NIM［J］.IEEE Transactions on Instrumentation and Measurement，2013，62（6），1789－1794.

［22］ 钱进，刘忠有，张小平，等.612nm He-Ne兰姆凹陷稳频激光系统［J］.红外与激光工程，2008，37（4）：192－195.

［23］ Yang Yan，Lu Wenjun，Zhao Jianting，et al.A two terminal-pair coaxial AC bridge with auto source balance at NIM［C］／／CPEM 2008 Digest，Washington DC，2012，690－691.

［24］ 周峰，岳长喜，雷民，等.基于电压串联加法的1000 kV国家工频电压计量标准［J］.计量学报，2012，33（6）：541－545.

［25］ Jiangtao Zhang，Xianlin Pan，Wenfang Liu，et al. Determination of Equivalent Inductance of Current Shunts at Frequency Up to 200 kHz［J］.IEEE Transactionson Instrumentation and Measurement，2013，62（6）：1664－1668.

［26］ Dai Dongxue，Ruan Yongshun，Wang Qi.Calibration Theory and Measurement Method of the Frequency Characteristics of the Four-Pair-Term inal Standard Capacitor［J］.ACTAMetrologica Sinica，2005，26（3）：263－266.

［27］ Haiming Shao，Feipeng Lin，Bo Liang，et al.DC 5 kA Current Ratio Standards Based on Series-parallel Selfcalibration DCCs［J］.IEEE Transactions on Instrumentation and Measurement，2013，62（11）：3093－3100.

Research for Reproducing SIUnit of Capacitance by the Calculable Capacitor w ith a Movable Guard Rod

LU Zu-liang1，HUANG Lu1，YANG Yan1，ZHAO Jian-ting1，QIAN Jin1，LUWen-jun1，LIU Zhong-you1，

ZHANG Zhong-hua1，LIU Xiu-ying1，WANG Jian-bo2，WANGWei1，HE Xiao-bing1
（1.National Institute of Metrology，Beijing 100029，China；
2.School of Physics Science and Engineering，Tongji University，Shanghai200092，China）

A new type calculable capacitorwith amovable guard rod has been built in National Institute of Metrology of China at the standard uncertainty of2×10－8.The SI unit of capacitance reproduced by the calculable capacitor depends on the axial length which ismeasured by a laser interferometer.However the huge integral number of the fringe is in general not given by the laser interferometer.In a classical approach the substitution measurementswere adopted to extend the integral number from a known smaller value to the bigger one.It needs some additive devices and complex operations.A novel approach is proposed.The required integral number is determined by the other capacitance standard with a lower accuracy，and the decimal number is determined by the capacitance bridgewith a transfer capacitor.The detailsof this approach and its advantages are presented.An experiment to check the linear is reported.

Metrology；Calculable capacitor；SI；Reproducing unit；Primary standard

TB971

A

1000-1158（2014）06-0521-07

10．3969／j．issn．1000-1158．2014．06．01

2014-06-11；

2014-07-24

国家自然科学基金（51207148，51207149）；“十一五”国家科技支撑计划项目（2006BAF06B04）

陆祖良（1948－），男，江苏南通人，中国计量科学研究院首席研究员，研究方向为电磁计量。luzl＠nim.ac.cn