基于Zernike矩的模糊与仿射混合不变量研究

蔡小帅,张荣国,李富萍,刘小君

(1.太原科技大学计算机科学与技术学院,太原030024;2.合肥工业大学机械与汽车工程学院,合肥230009)

基于Zernike矩的模糊与仿射混合不变量研究

蔡小帅1,张荣国1,李富萍1,刘小君2

(1.太原科技大学计算机科学与技术学院,太原030024;2.合肥工业大学机械与汽车工程学院,合肥230009)

Zernike矩作为形状描述子,其信息冗余度低且对噪声不敏感,在图像特征提取和模式识别中得到了广泛应用。为提高Zernike矩对含有模糊和仿射图像的形状描述能力,提出一种基于Zernike矩的形状描述子,该描述子使用规范化方法构造Zernike矩的仿射不变量,结合Zernike矩的模糊不变量得到Zernike矩的模糊和仿射混合不变量。将该矩混合不变量作为形状描述子描述图像的形状特征,并与几何矩模糊和仿射混合不变量进行对比实验,结果表明,Zernike矩的模糊和仿射混合不变量在混合形变下形状描述能力较强,具有不变性,并且对噪声的鲁棒性较好。

Zernike矩;形状描述子;规范化方法;点扩展函数;仿射不变量;模糊不变量

1 概述

在图像的实际采集过程中,由于对焦错误、设备移动、环境及其他方面的影响,使采集到的图像往往有不同程度降质,其中包括模糊形变和仿射形变。传统的形状描述子对这类图像的描述能力弱,因此对这些降质图像中物体的形状描述成为计算机视觉、模式识别及医学成像等领域的重要任务。近年来,国内外对模糊和仿射形变图像的形状描述及识别方法研究较为广泛和深入的是矩不变量方法［1］。对于仿射不变量,文献［2］采用代数不变量的理论获得了几何矩仿射不变量;文献［3］提出了采用规范化方法构建仿射不变量。在模糊不变量方面,文献［4］引入点扩展函数法得到几何矩模糊不变量。后来,文献［5］提出利用点扩展函数的相关理论得到同时对模糊和仿射变换具有不变性的矩混合不变量;文献［6］采用直接构造法和规范化方法得到了几何矩模糊和仿射混合不变量。然而几何矩都是非正交的,有一定的信息冗余且噪声敏感度高。文献［7］认为正交矩的形状描述能力强、噪声鲁棒性好且信息冗余度低。因此,文献［8］提出了Legendre矩的模糊和仿射混合不变量;文献［9］构造了一种Techebichef矩的模糊和仿射混合不变量。虽然Zernike矩的各阶矩相互独立、信息冗余度小且抗噪能力强,得到了广泛的应用和研究。但除了文献［10］提出的Zernike矩的模糊和旋转混合不变量和文献［11］介绍的Zernike矩的相似和模糊混合不变量外,还没有看到同时对模糊和仿射形变具有不变性的不变量的相关报道,因此构造相应的Zernike矩不变量处理含有混合形变的图像有一定的研究价值。

在上述研究工作的基础上,本文提出一种基于Zernike矩的形状描述子,该描述子采用规范化方法消除仿射变换中仿射参数的影响,利用点扩展函数相关理论得到模糊不变量,通过两者结合得到同时对模糊和仿射变换具有不变性的Zernike矩,并通过实验进行了验证。

2 Zenike矩和几何矩介绍

2.1 Zernike矩的定义

p阶的Zernike多项式为定义在极坐标系下单位圆上的复数多项式Vpq(x,y),表达式如下:

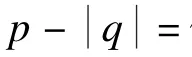
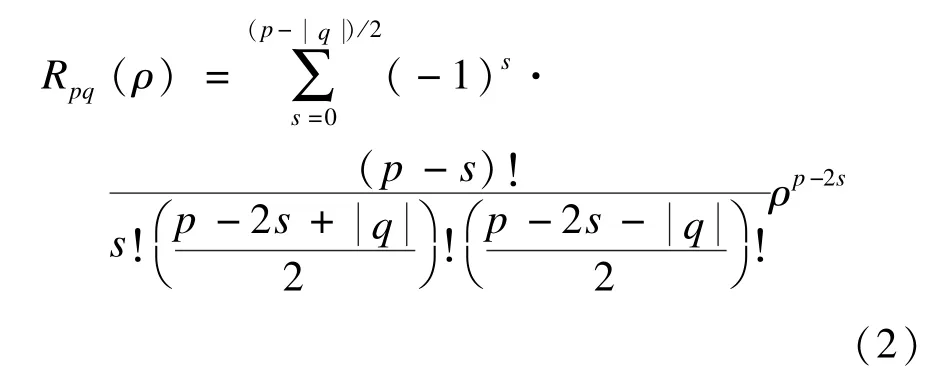
令k=p-2s,Rpq(ρ)关于ρ的幂级数形式如下:

其中,(n-k)为偶数。

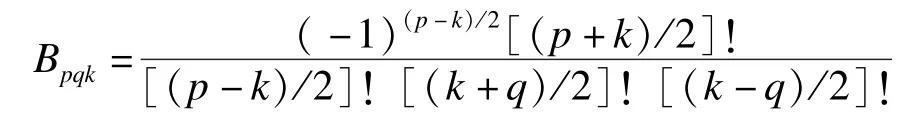
以正交Zernike多项式为核的阶数为p,重复度为q的Zernike矩的定义为:

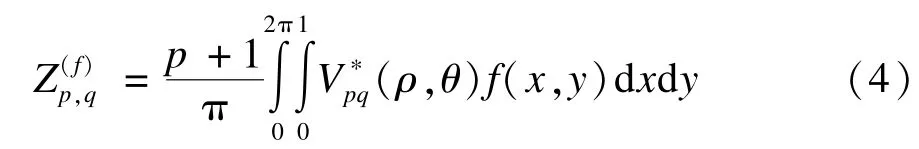
由式(4)和式(3)可以得到Zernike矩与几何矩的关系如下［12］:

其中,t=(k-q)/2,且p-k为偶数。

2.2 几何矩的定义

令f(x,y)为图像的密度函数,则它的(p+q)阶几何矩函数的定义如下:

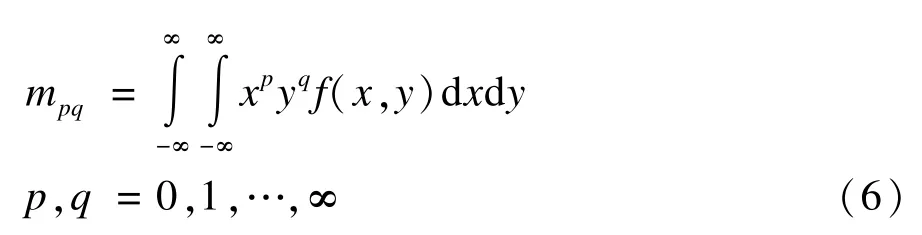
(p+q)阶中心矩表示为:

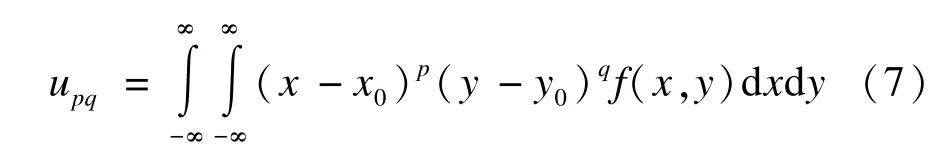
其中,p,q=0,1,…,∞且x0=m10/m00,y0=m01/m00。

3 基于Zernike矩的模糊和仿射混合不变量

3.1 Zernike矩的模糊不变量

图像的模糊形变过程可以表示为原图像f(x,y)和一个任意中心对称的点扩展函数(PFS)h(x,y)的卷积,即:

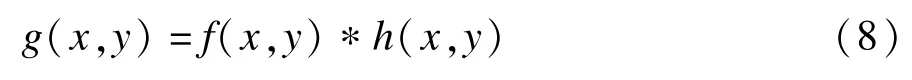
该点扩展函数h(x,y)具有如下性质:

针对这个点扩展函数 h(x,y),可以构造出Zernike矩的模糊不变量,表示如下［11］:

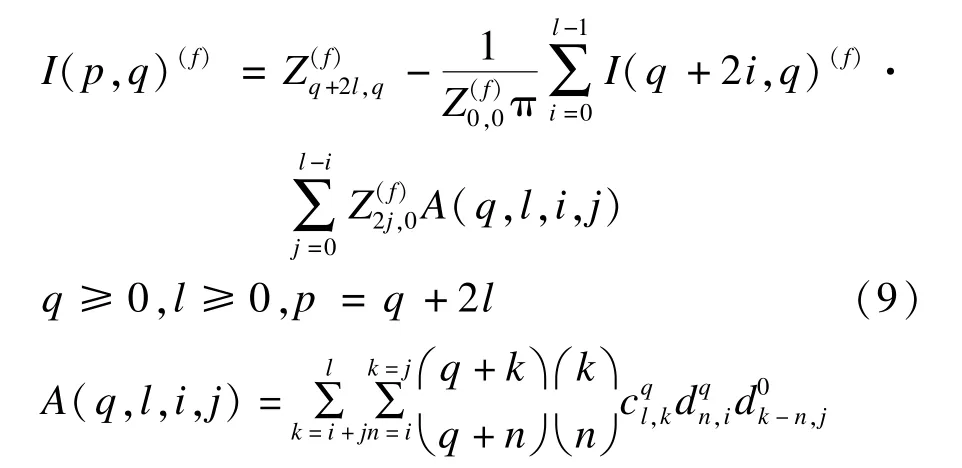
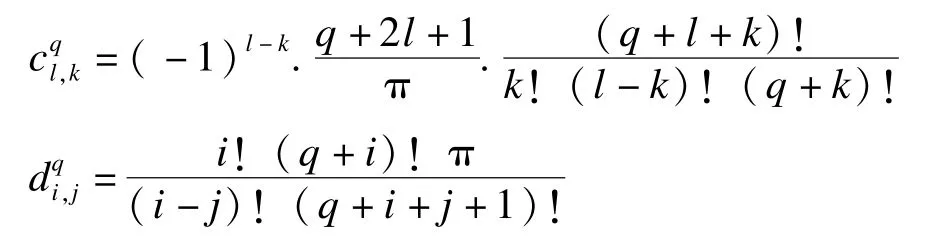
3.2 Zernike矩的仿射不变量

仿射变换是一种从空间坐标(x,y)变换到新的坐标(u,v)的线性变换,可写成如下矩阵表示形式:

本文运用中心矩代替几何矩消除平移变换的影响,然后运用由Rothe提出的XSR分解法把矩阵A分解成为1个x剪切矩阵,1个均匀缩放矩阵和1个旋转矩阵3个矩阵,其表示如下:

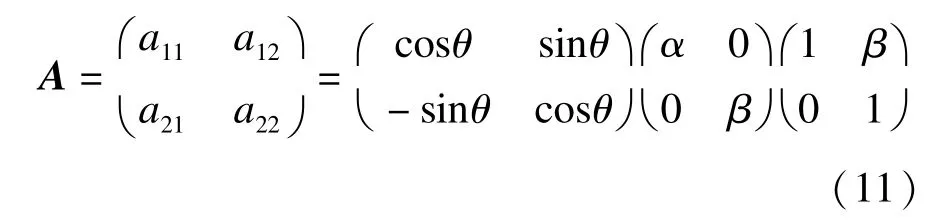
(1)x剪切不变量

(2)均匀缩放不变量

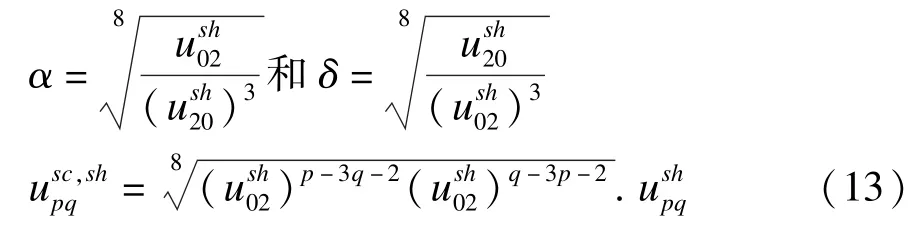
(3)旋转不变量

把下面的方程规范化为0得到变换参数θ:

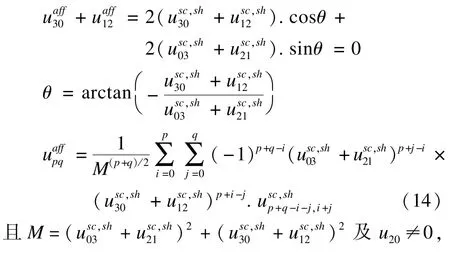
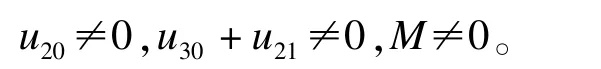
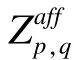
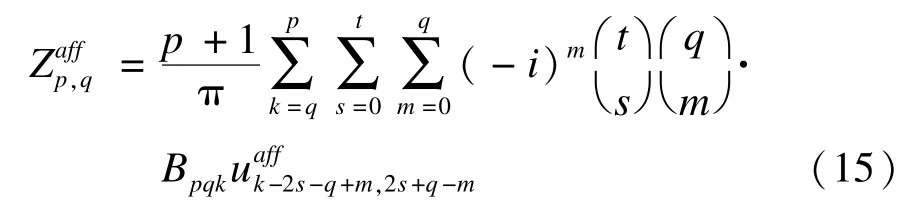
3.3 Zernike矩模糊和仿射混合不变量

仿射不变量的任意线性函数仍是仿射不变的。使用式(15)替代式(9)中的Zernike矩函数,即可获得 Zernike矩模糊和仿射混合不变量,表示如下:

4 实验结果与分析

下面的实验用来说明并验证本文所提出的Zernike矩模糊和仿射混合不变量(ZCMI)的图像描述能力、对模糊和仿射变换的不变性及噪声鲁棒性。

4.1 图像描述能力分析

本文实验平台为:Windows XP,Matlab R2012(a), CPU:Intel Celeron(R),1.86 GHz,ROM:1 GB。

首先测试ZCMI对于退化图像(包括仿射和模糊)的描述性能,如图1、图2所示。图像lena和图像birthday,图1(a)和图2(a)为图像的原始图像,图1(b)和图2(b)为仅发生了仿射变换后的图像,图1(c)～图1(e)和图2(c)～图2(e)为不仅发生了仿射变换并且分别同时加入了模糊参数为［3 3］的平均模糊、模糊参数为［5 5］的高斯模糊、模糊参数为5的圆形区域均值模糊及模糊参数为9的运动模糊,其中仿射变换中仿射矩阵各元素值为a11=1.483,a12=2,158,a13= -0.723,a14= 0.850。为了测试ZCMI对退化图像的描述能力,将分别通过对图1和图2中各图的矩不变量值对此予以验证。表 1和表 2分别为图 lena和图birthday各变换图像的8个矩不变量值,其中,μ代表6幅图像各阶矩的矩平均值,σ代表平均误差, σ/μ(%)代表平均误差率。从表1和表2可以看出,经过模糊和仿射变换的各图像的矩不变量值并不是恒定不变的,而是在一定的范围内波动,但平均误差率低,整体较为稳定,说明这些矩不变量值的波动程度是可以接受的,验证了ZCMI对退化的图像具有较好的形状描述能力。

图1 图像lena的仿射和模糊图像

图2 图像birthday的仿射和模糊图像

表1 图像lena的ZCMI矩不变量

表2 图像birthday的ZCMI矩不变量

4.2 不变性验证及噪声鲁棒性

本文实验用来验证ZCMI对模糊和仿射形变的不变性以及对噪声的鲁棒性。实验图像为图像lena,图1(a)为原始图像,图1(c)～图1(f)分别对图像加入了仿射和模糊形变。为了测试本文提出的描述子对噪声的鲁棒性,图 1(c),图 1(d)和图1(e),图1(f)中分别加入了不同密度的高斯噪声和椒盐噪声,其噪声密度为0.01～0.20;两幅图像的矩不变量值之间的相对误差可以表示为:

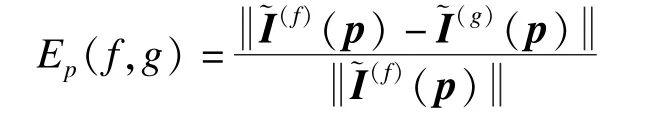
其中,f和g分别用来表示原始图像和其发生某种形变后的图像。相对误差在此用来衡量形状描述子的不变性。其中,~(p)及I(p)为向量;,,p≥ 0,且I(p,q)在式(16)中已给出定义。

图3为分别使用本文提出ZCMI和Zhang等提出的几何矩模糊和仿射不变量(GCMI)计算出的原始图像和形变图像的矩不变量值之间相对误差的变化情况。图3的2条曲线分别表示使用GCMI和本文提出的ZCMI获得的相对误差。由图3(a)、图3(c)、图3(d)可以看出,在图像包含有仿射形变和不同模糊形变的条件下,加入不同密度的噪声时,与GCMI相比,随着噪声密度的增大,ZCMI仍能够获得较小的相对误差;虽然图3(b)中出现个别不稳定现象,但整体相对误差仍然相对较小。因此,实验结果表明在不同的混合形变和不同的噪声作用下,与GCMI相比,本文提出ZMCI不变性及噪声的鲁棒性较好。

图3 不同矩混合不变量的相对误差

5 结束语

本文提出一种基于Zernike矩的模糊和仿射形变具有不变性的形状描述子。该描述子采用规范化方法消除仿射变换的影响,得到Zernike矩仿射不变量;将其与用中心对称点扩展函数方法得到的Zernike矩模糊不变量相结合构造出Zernike矩模糊和仿射混合不变量。实验结果表明,与几何矩模糊和仿射混合不变量相比,本文提出的Zernike矩模糊和仿射不变量描述能力强、不变性好,且对噪声敏感度小。

［1］ Flusser J,Suk T.Moment and Moment Invariants in Pattern Recognition［M］.Oxford,UK:John Willey& Sons,2009:1-5.

［2］ Flusser J,Suk T.Pattern Recognition by Affine Moment Invariants［J］.Pattern Recognition,1993,26(1): 167-174.

［3］ Rothe I,Susse H,Voss K.The Method of Normalization to Determine Invariants［J］.IEEE Transactions on Pattern Anal.Mach.Intel.,1996,18(4):366-375.

［4］ Flusser J,Suk T.Degraded Image Analysis:An Invariant Approach［J］.IEEE Transactions on Pattern Anal.Mach.Intell.,1998,20(6):590-603.

［5］ Suk T,Flusser J.Combined Blur and Affine Moment Invariants and Their use in Pattern Recognition［J］.Pattern Recognition,2003,36(12):2895-2907.

［6］ Zhang Y N,Wen C Y,Zhang Y,et al.Determination of Blur and Affine Combined Invariants by Normalization［J］.Pattern Recognition,2002,35(1):211-221.

［7］ Shu H Z,Zhou J,Han G N,et al.Image Reconstruction from Limited Range Projections Using Orthogonal Moments［J］.Pattern Recognition,2007,40(2):670-680.

［8］ 戴修斌,张 辉,舒华忠,等.基于正交矩模糊和仿射混合不变量的图像识别算法［J］.东南大学学报:自然科学版,2011,41(1):52-57.

［9］ Li Q,Zhu H Q,Liu Q.Image Recognition by Combined Affine and Blur Tchebichef Moment Invariants［C］// Proceedings of the 4th International Congress on Image and Signal Processing.［S.1.］:IEEE Press,2011: 1517-1521.

［10］ Zhu H Q,Liu M.Combined Invariants to Blur and Rotation Using Zernike Moment Descriptors［J］.Pattern Analysis and Applications,2010,13(1):309-319.

［11］ Chen B J,Shu H Z.Combined Invariants to Similarity Transformation and to Blur Using Orthogonal Zernike Moments［J］.IEEE Transactions on Image Processing, 2011,20(2):345-360.

［12］ Teague M R.Image Analysis via the General Theory of Moments［J］.Journal of Optimal Society of American, 1980,70(8):920-930.

编辑 索书志

Study on Blur and Affine Combined Invariants Based on Zernike Moment

CAI Xiaoshuai1,ZHANG Rongguo1,LI Fuping1,LIU Xiaojun2
(1.School of Computer Science and Technology,Taiyuan University of Science and Technology,Taiyuan 030024,China;
2.School of Mechanical and Automotive Engineering,Hefei University of Technology,Hefei 230009,China)

Zernike moment,as a shape descriptor,has been widely used in image characteristics extraction and pattern recognition.It is low information redundancy and not sensitive to noise.To improve the shape description capability of the images which are degraded by combined blur and affine transformation,a new shape descriptor based on Zernike moment is proposed.The normalization method is used to construct affine invariants of Zernike moment.The combined blur and affine moment invariants of Zernike moment is achieved by the help of the blur invariants.The combined moment invariants is used as the shape descriptor to describe the shape feature of images,and is implemented comparison with the combined affine and blur invariants based on geometric moment with relative error.Experimental results show that the combined blur and affine invariants of Zernike moment can get better shape description and invariance in combined degrades,and robustness to noise.

Zernike moment;shape descriptor;normalization method;point spread function;affine invariant; blur invariant

1000-3428(2014)11-0215-05

A

TP391

10.3969/j.issn.1000-3428.2014.11.042

国家自然科学基金资助项目(51075113);山西省自然科学基金资助项目(2013011017);高等学校博士基金资助项目(20122025);太原科技大学校研究生创新基金资助项目(20125024)。

蔡小帅(1987-),女,硕士研究生,主研方向:图形图像处理;张荣国,教授;李富萍,讲师;刘小君,教授、博士生导师。

2013-11-05

2013-12-31E-mail:zhrgty@163.com

中文引用格式:蔡小帅,张荣国,李富萍,等.基于Zernike矩的模糊与仿射混合不变量研究［J］.计算机工程,2014, 40(11):215-219.

英文引用格式:Cai Xiaoshuai,Zhang Rongguo,Li Fuping,et al.Study on Blur and Affine Combined Invariants Based on Zernike Moment［J］.Computer Engineering,2014,40(11):215-219.