改进的三角网格表面近似测地线算法

施逸飞,熊岳山,朱晨阳,施 鹏

(国防科学技术大学计算机学院高性能计算国家重点实验室,长沙410073)

改进的三角网格表面近似测地线算法

施逸飞,熊岳山,朱晨阳,施 鹏

(国防科学技术大学计算机学院高性能计算国家重点实验室,长沙410073)

三角网格表面的测地线计算问题可转化为三角网格表面两点间的最短路径计算问题,为了快速地计算三角网格表面测地线,提出一种基于缩小最短路径搜索区域的三角网格表面近似测地线算法。将三角网格沿坐标系三坐标轴方向进行空间单元划分,使用A*算法求出两点间的最短路径盒子序列,进而得到新的搜索区域,计算三角网格上两点间的最短路径,迭代细分最短路径邻域内的边以构造新的网格求解测地线。实验结果表明,该算法能够快速准确地计算出三角网格表面任意两点间的近似测地线,有效解决大型三角网格上最短路径计算速度慢的问题,计算速度较改进前的算法提高了10倍～59倍。将该算法应用到虚拟肝脏手术系统的区域标定中,可满足虚拟场景中对计算实时性和效果真实性的要求。

测地线;三角网格;空间单元划分;A*算法;虚拟肝脏手术;触觉交互设备

1 概述

计算三角网格模型表面两点间的测地线是计算几何中的一个基础性问题,被广泛应用于计算机图形学、地理信息系统、机器人学、虚拟现实、虚拟手术等领域,有重要的理论意义与应用价值。

目前已有多种针对三角网格模型的测地线算法,可分为2类:(1)计算三角网格上一点与其他所有点之间的测地线算法;(2)计算给定两点间的测地线算法。在第(1)类测地线算法中,文献［1］提出了使用连续的Dijkstra算法计算测地线的MMP算法,该算法的时间复杂度为O(n2logn);文献［2］证明了MMP算法的实际运算速度比理论速度快得多,并提出了一种复杂度为O(nlogn)的测地线近似算法;文献［3］提出了著名的CH算法,该算法选定网格上一点作为根结点,以网格的边为叶子结点,构造一棵序列树,任意点到选定点的测地线可以在O(n2)内计算得到;文献［4］提出一种时间复杂度为O(n)的测地线近似算法,但事先需要对模型进行长时间预处理;文献［5］将热学扩散方法引入测地线的计算,将近似测地线的计算速度提高了一个数量级。在第(2)类测地线算法中,文献［6］将三角网格模型转化为带权图,利用Dijkstra算法计算图上两点间的最短路径,再细分最短路径邻域上的边来更新带权图,反复迭代计算最短路径得到两点间的近似测地线;文献［2］在MMP算法的基础上引入启发性函数,使用连续的A*算法求取两点间测地线。

本文在文献［6］的基础上,针对Dijkstra算法计算最短路径速度较慢的问题,提出一种基于空间单元划分的最短路径搜索区域缩小算法,在最短路径计算前排除明显不在最短路径附近的边,提高最短路径的计算速度。

2 最短路径搜索区域缩小算法

基于空间单元划分的最短路径搜索区域缩小算法的思想为:先构造一个由多个大小相等的正方体盒子构成的搜索空间,求解盒子中心点间的最短路径［7-8］,然后由最短路径上盒子及其领域中的网格构成新的搜索区域,在该搜索区域中可求出较精确的最短路径视为测地线。

将三角网格模型G进行空间单元划分,设Xmax,Xmin,Ymax,Ymin,Zmax,Zmin分别为三角网格模型在X,Y,Z轴上的最大值和最小值,沿X轴方向所划分的盒子数量为m,则单个盒子的长度GridSize为:

沿Y,Z方向划分的盒子数量n,l分别为:

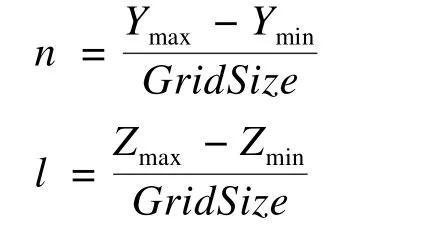
三角网格模型就被分为m×n×l个正方体盒子。

遍历三角网格模型,找到每一个三角面片所在的正方体盒子,如果一个三角面片在多个正方体盒子中,则以三角面片质心所在的盒子为准。将包含三角面片的正方体盒子视为有效盒子,删除不是有效盒子的正方体盒子。图1是对Bunny模型进行空间单元划分得到的所有正方体盒子和有效盒子。

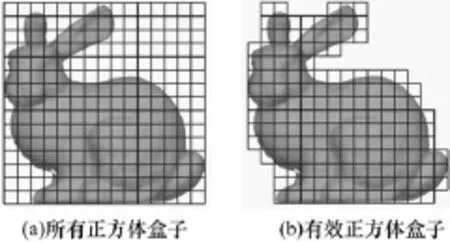
图1 Bunny模型的空间单元划分

使用A*算法求解测地线两端点所在盒子间的最短路径［9］。A*算法是一种启发式的搜索算法［10］,它把当前结点与起始节点的耗散g(n)和与目标节点的耗散h(n)结合起来对节点进行评价:

本文将g(n)设为起始盒子到当前盒子的距离,h(n)设为目标盒子到当前盒子的距离的一半,用f(n)来评价结点。

设给定测地线起点所在盒子的序号为indexs,终点所在盒子序号为indexe,则使用A*搜索算法计算得到的indexs到indexe的最短路径L为一个相互连接的盒子序列,该盒子序列大致体现了两点间测地线的形态。取出盒子序列以及其n-邻域上盒子中包含的三角面片构成新的测地线搜索网格区域G′,两点间的测地线必定位于新的搜索区域中。

整个算法可描述为:

算法SearchAreaRefining(G)输入 完整的三角网格模型G

输出 优化后的三角网格搜索区域G′

(1)将模型G所在空间划分为若干个相等的正方体盒子。

(2)将含有三角面片的盒子记为有效盒子,删除非有效的盒子。

(3)使用A*算法计算测地线起点和终点所在盒子indexs和indexe间的最短路径,得到盒子序列L。

(4)取出盒子序列L及其n-领域上的盒子内所包含的三角面片,得到优化后的搜索区域G′。

图2 Bunny模型搜索区域的优化

图2是对Bunny网格模型搜索区域进行优化前后的对比,经过上述方法的优化,Bunny模型上两点间最短路径的搜索区域三角面片数量由原来的5 328个减小为556个,搜索区域大大缩小,在三角网格表面计算最短路径的速度将显著提高。判断三角面片属于哪个正方体盒子需要遍历整个网格,计算量较大,但可以通过预处理提前计算完成,不会占用该算法的计算时间。因为计算最短路径使用A*算法,得到盒子序列的计算无需遍历所有有效盒子,同时有效盒子的数量往往比三角面片数量少得多,所以上述方法可以在很短的时间内得到盒子序列及其1-领域内的盒子。A*搜索算法的时间复杂度为O(n),通过盒子序列得到新的搜索区域的时间复杂度为O(1),本文算法总的时间复杂度为

O(n)。

3 迭代细分的近似测地线计算

本文算法可以计算三角网格上任意两点间的测地线,测地线的起点和终点无需是三角网格的顶点。若三角网格面上的某点不为三角网格的顶点,可对该点所在的三角面片进行剖分,这样任意三角网格表面的点都可转化为三角网格的顶点。如图3所示,剖分三角形ABC,可使点D成三角网格的顶点。

图3 三角形剖分策略

三角形剖分完成后,可采用文献［6］的方法计算三角网格表面任意两顶点间的近似测地线。文献［6］的方法首先将原三角网格模型转换成无向邻接图,在图中使用Dijkstra算法求得两顶点间的最短路径,接着细分最短路径领域内的边,使新加入的边从原三角面片的内部通过,构成新的无向邻接图。反复细分最短路径领域内的边,并计算更新后图中两点间的最短路径,直到前后两次最短路径之差小于给定阈值,求得的最短路径即为两点间的近似测地线。

图4是使用文献［6］中方法计算最短路径的结果,图4(a)中的粗线为初始网格中的最短路径,图4(b)中的粗线为近似测地线。

图4 文献[6]方法的计算结果

文献［6］中方法需要在整个网格范围内进行最短路径计算,由于三角网格模型通常规模较大,该方法的主要时间消耗在初始最短路径的计算中。使用基于空间单元划分的最短路径搜索区域缩小算法进行优化,可以提前排除与最短路径距离较远的边,缩小搜索区域,减小初始最短路径的计算时间。

4 算法实验与分析

为了验证本文算法,在 PC机(CPU为双核1.40 GHz,RAM 2 GB)上进行了实验,选取图5所示的5个不同规模的三角网格模型,计算其中选定两点间的测地线,结果如表1所示。可以看出,本文算法计算速度优于文献［6］中的算法,三角网格模型规模越大,优势越明显。对于由69 451个三角面片构成的Bunny模型,本文算法的计算速度是文献［6］算法的59倍,计算效率明显提高。

图5 三角网格模型和测地线

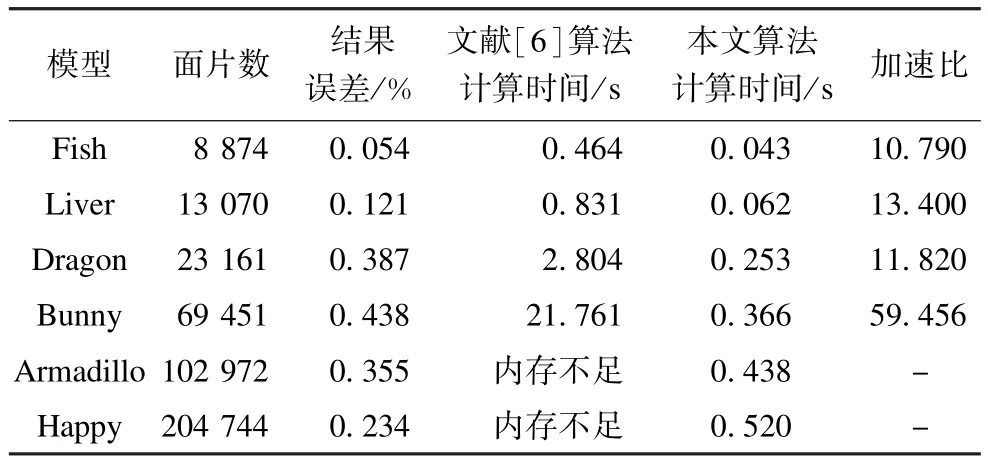
表1 求解模型表面测地线的实验数据

图5中所有模型的测地线均可被正确求解,证明了本文算法是切实可行的,且鲁棒性好。对于较复杂的模型,可以通过增加盒子划分数量的同时增大提取最短路径盒子序列的n-邻域操作中的n来提高结果的精度。

在含有13 070个三角面片的Liver模型上进行多组测地线计算,规定测地线相对长度为测地线长度除以模型长方体包围盒对角线的长度,图6为计算结果。可以看出,模型大小一定时,测地线越短,加速比越大。由于本文算法避免了在全局范围内进行Dijkstra计算,计算时间只和测地线经过的三角面片数量有关,而与模型的大小无关。本文算法适合大规模三角网格上的测地线计算,对于大规模三角模型上短距离的测地线计算有明显的时间优势。

图6 Liver模型上不同长度测地线的实验数据

5 虚拟肝脏手术区域标定

虚拟肝脏手术是虚拟现实技术在现代医学中的重要应用,它对虚拟场景的真实感、精确度、实时性和交互性的要求比普通虚拟现实系统更高［11］。虚拟肝脏区域标定是虚拟肝脏手术的重要步骤之一,是一个典型的三角网格上测地线的计算问题。区域标定操作使用虚拟手术电刀与肝脏表面的三角网格接触,采集得到一连串离散点,计算这些离散点间的测地线。测地线是贴于三角网格表面的最短线段,依次连接相邻两离散点的测地线可以得到一条长曲线,模拟电刀在肝脏表面划过的动作,如同用笔在纸上划线。

本文虚拟肝脏手术系统的硬件为PC机(CPU四核3.40 GHz,RAM 8 GB)以及SensAble公司生产的PHANTOM触觉交互设备［12］,系统软件开发基于图形开发包OpenGL和力反馈开发包OpenHaptic,OpenGL用来完成图形的绘制工作, OpenHaptic用来完成触觉系统的交互工作。为了模拟真实手术场景,在该系统的区域标定步骤中, PHANTOM触觉交互设备在肝脏表面的采点速率不能低于每秒3个,相邻两点间的测地线必须在0.33 s内计算完成,若在整个三角网格模型范围内进行Dijkstra最短路径计算将无法满足实时计算的要求。

PHANTOM采集到的点间距离通常不大,使用本文算法可以缩小最短路径搜索区域,提高计算效率。将肝脏模型划分为15×10×10个正方体盒子,近似测地线的计算进行5次迭代求解得到,离散点间的近似测地线如图7中线段所示。测地线的平均计算时间为 0.03 s,测地线的平均计算误差为0.07%,可以满足虚拟场景的实时性和真实性的要求。

图7 肝脏手术区域标定的模拟效果

6 结束语

本文提出了基于空间单元划分的最短路径搜索区域缩小算法,对三角网格表面两点间近似测地线的算法进行了改进,使近似测地线迭代计算中初始最短路径计算的速度明显提高。实验结果表明,该算法有效地解决了大型网格表面近似测地线计算效率低下的问题,近似测地线的计算时间较原算法大大减少。将该算法应用于虚拟肝脏手术系统中,满足了模拟肝脏手术表面区域标定对实时性和真实性的需求。

对于复杂的、表面起伏较大的三角网格中测地线的计算,必须采用减小空间单元划分的密度或者扩大有效盒子邻域的方法来保证结果的正确性,这在一定程度上降低了计算效率,因此,如何根据三角网格的分布特征对模型进行非均匀单元划分,提高算法的效率和精确性,是下一步需要研究的内容。

［1］ Mitchell J S B,Mount D M,Papadimitriou C H.The Discrete Geodesic Problem［J］.SIAM Journalon Computing,1987,16(4):647-668.

［2］ Surazhsky V,Surazhsky T,Kirsanov D,et al.Fast Exact and Approximate Geodesics on Meshes［J］.ACM Transactions on Graphics,2005,24(3):553-560.

［3］ Chen J,Han Y.Shortest Paths on a Polyhedron［C］// Proc.of the 6th Annual Symposium on Computational Geometry.［S.l.］:ACM Press,1990:360-369.

［4］ Xin Shiqing,Ying Xiang,He Ying.Constant-time All-pairs Geodesic Distance Query on Triangle Meshes［C］//Proc.of ACM SIGGRAPH Symposium onInteractive 3D Graphics and Games.［S.l.］:ACM Press,2012:31-38.

［5］ Crane K,Weischedel C,Wardetzky M.Geodesics in Heat:A New Approach to Computing Distance Based on Heat Flow［J］.ACM Transactions on Graphics,2013,32(5):152.

［6］ Kanai T,Suzuki H.Approximate Shortest Path on a Polyhedral Surface and Its Applications［J］.Computeraided Design,2001,33(11):801-811.

［7］ 杨 斌,范媛媛,王继东.点云模型上近似测地线的计算［J］.计算机应用,2011,31(4):1050-1052.

［8］ 杜培林,屠长河,王文平.点云模型上测地线的计算［J］.计算机辅助设计与图形学学报,2006,18(3): 438-442.

［9］ Xin Shiqing,Wang Guojin.Applying the Improved Chen and Han's Algorithm to Different Versions of Shortest Path Problems on a Polyhedral Surface［J］.Computeraided Design,2010,42(10):942-951.

［10］ Rusfell S,Norvig P.Artificial Intelligence——A Modern Approach［M］.2nd ed.New Jersey,USA:Prentice Hall Press,2004.

［11］ Wang Yanzhen,Xiong Yueshan,Xu Kai,et al.vKASS:A Surgical Procedure Simulation System for Arth-roscopic Anterior Cruciate Ligament Reconstruction［J］.Computer Animation and Virtual Worlds,2013,24(1):25-41.

［12］ 施 鹏,熊岳山,徐 凯,等.虚拟肝脏手术中实时动态渗血效果模拟［J］.计算机应用,2013,33(10):2911-2913,2917.

编辑 顾逸斐

Improved Surface Approximate Geodesic Algorithm on Triangle Mesh

SHI Yifei,XIONG Yueshan,ZHU Chenyang,SHI Peng
(State Key Laboratory of High Performance Computing,School of Computer, National University of Defense Technology,Changsha 410073,China)

The computation of approximate geodesics algorithm on triangle mesh can be transformed to the computation of the shortest path on triangle mesh.In order to figure out the geodesics on triangle mesh efficiently,an improved approximate geodesics algorithm is presented.A weighted graph is constructed by splitting triangle mesh along the Cartesian coordinate axes,thus the shortest path on lattice can be computed by A*algorithm and a new region of search can be defined.The neighboring edges of the shortest path are iteratively subdivided to construct a new weighted graphs to approach the geodesic.Experimental results show the improved algorithm can figure out the geodesics precisely and efficiently.The speed up ratio of the algorithm range is increased between 10 and 59.A region labeling method on virtual liver surgery based on the improved algorithm is also proposed,which can meet the computational real-time and quality requirements of virtual scene.

geodesic;triangle mesh;division of space unit;A*algorithm;virtual liver surgery;haptic interface device

10.3969/j.issn.1000-3428.2014.11.044

1000-3428(2014)11-0225-04

A

TP391

国家自然科学基金资助项目(61379103,61202333,61303185);高等院校博士点专项基金资助项目(20104307110003)。

施逸飞(1991-),男,硕士,主研方向:计算机图形学,虚拟现实;熊岳山,教授、博士、博士生导师;朱晨阳、施 鹏,硕士。

2013-10-21

2013-12-19E-mail:jerrysyf@gmail.com

中文引用格式:施逸飞,熊岳山,朱晨阳,等.改进的三角网格表面近似测地线算法［J］.计算机工程,2014,40(11):225-228.

英文引用格式:Shi Yifei,Xiong Yueshan,Zhu Chenyang,et al.Improved Surface Approximate Geodesic Algorithm on Triangle Mesh［J］.Computer Engineering,2014,40(11):225-228.