基于优先选择和记忆效应的观点动力学研究

黄庆花,宋玉蓉

(南京邮电大学自动化学院,南京210046)

基于优先选择和记忆效应的观点动力学研究

黄庆花,宋玉蓉

(南京邮电大学自动化学院,南京210046)

针对社会群体中观点共享的现象,考虑节点间交互存在偏好选择(优先选择),以及节点对异己观点存在记忆效应,扩展Deffuant模型,建立一种新的观点动力学模型。采用优先选择策略,使非均匀网络达成一致观点;在网络只选用优先选择策略而不考虑节点记忆效应时,网络一致性观点的形成仍依赖于置信值的取值。在网络考虑节点记忆效应后,不仅能够促进网络达成一致观点,而且在置信值很小的情况下,网络也能达成一致观点。研究结果表明,随着置信值的增加,网络达成一致观点所需的最小观点更新次数逐渐减少。

Deffuant模型;优先选择;记忆效应;观点动力学;非均匀网络

1 概述

观点动力学主要研究社会经济系统中个体之间的决策以及在外界公共信息作用下,人群中个体对某些特定事件或事物所持不同观点的形成(formation)和演化(evolution)等现象［1-3］,并分析观点的一致性(consensus)与多样性(diversity)保持等问题。目前大多数研究工作主要是通过建立模型的方式对现实问题进行仿真研究,现有研究表明观点动力学模型主要分为两大类:第1类为离散观点值模型,如Ising模型［4］、选民模型(voter model)［5-6］、多数统治模型(majority rule model)［7-8］和Sznajd模型［9］;第2类为连续观点值模型,如边界信任模型(bounded confidence model)［10-11］等。在对观点动力学模型的研究过程中,过去研究者大多采用第1类离散观点值模型,模型中的观点呈二值化形态。而在现实生活中,人们对于某些事件的观点往往不是简单的离散值,因此出现了第2类连续观点值模型。在第2类模型中,Deffuant模型［10］的观点呈连续分布形态,是当前研究观点动力学问题普遍采用的模型。

随着观点动力学模型研究的深入开展,网络一致性观点的形成引起了广泛的关注。目前针对不同的观点动力学模型,研究的主要内容具体如下:基于选民模型,文献［12］研究表明网络的拓扑结构和观点更新策略对网络达成一致性观点状态的时间有很大的影响,实验中存在的最优值a(a是自适应幂指数,用来控制节点选择各观点的概率)能够减少网络收敛到一致观点的时间;文献［13］主要研究节点在同一时刻拥有2个观点的记忆过程,得到记忆效应不仅能够改变模型的行为,而且能够加速网络一致性观点形成的结论。基于Deffuant模型,文献［14］重点研究在自适应网络中观点演化的过程,节点进行观点交互时,若节点间观点差值不大于置信值d,节点才进行观点更新,实验表明网络拓扑的自适应性促进了一致性观点的形成,但也可能促使一致性观点分裂;文献［15］研究表明节点进行观点交互时,若节点间观点差值大于置信值d,节点以一定的概率进行观点更新,这有利于网络中观点达成一致性。

当前对于连续观点值模型的研究较多的是局限于节点间观点差值小于置信值d时,节点进行观点更新。而在实际社交生活中,当个体与他人的观点差值大于置信值d时,虽然多数人不会立即改变自己的观点,但在经历多次观点交互冲突且对冲突进行记忆后,个体可能会动摇所持有的观点,进而改变观点。

此外,社会群体中个人的态度、想法、观点往往容易受其他个体的影响,个体比较偏好于与身边中熟悉的、有影响力的个体进行交流,符合“富者更富”或者“马太效应”［16］现象。

本文结合选民模型中提到的记忆效应,以及真实社会生活中存在的群体间优先选择(偏好选择)某些个体进行观点交互的事实,考虑扩展Deffuant模型,提出一个新的观点动力学模型。该模型采用优先选择交互策略,当节点进行观点交互时,若节点间观点差值大于置信值d,节点通过叠加记忆值来达到记忆阈值进行有限次观点更新。此外,分析了优先选择策略和记忆效应对网络一致性观点形成的影响。

2 Deffuant模型

2.1 基本Deffuant模型

在Deffuant模型中,网络每个节点随机分配一个观点值O,该观点值取值范围为0～1。在t时间步(演化代数),节点i以等概率pi在其邻居中随机选择交互节点,概率pi按下式计算:其中,Vi表示节点i的邻居集。若节点j被选为交互节点,且交互过程中两节点观点差值ΔOij(t)小于或等于置信值d,(即ΔOij(t)=|Oi(t)-Oj(t)|≤d,其中,Oi(t)和Oj(t)分别表示t时刻节点i和j的观点值),则i和j按式(2)进行观点更新:

其中,u是收敛参数(u∈［0,0.5］)。本文假设u= 0.5,表示两节点的观点更新结果为它们上一时刻观点的算数平均值。也即在t+1时刻,节点i和j按式(3)进行观点更新:

2.2 考虑优先选择策略与记忆效应的模型

在真实社会网络中,个体会偏好于与身边人群中具有影响力的个体进行观点交流。考虑到上述现象,本文在与社会网络相对应的节点网络中,以节点度的大小作为交互节点选择的标准,认为度大的节点影响力也较大,相应的,其被选择作为交互节点的概率会较大。将上述选择交互节点的方式称为优先选择策略。

定义节点间的交互规则如下:每个时间步t,节点i以一定的概率pij在其邻居中优先选择交互节点j,概率pij为:

其中,kj表示节点j的度,j∈Vi表示节点j属于节点i的邻居集。

假设M(i,t)为节点i在t时刻的记忆值,Mt为记忆阈值,约定初始时刻所有节点的记忆值为0,即M(i,0)=0。约定若节点与比其观点小的节点进行观点交互时,产生的交互记忆值为负记忆值,反之为正记忆值,并且认为节点的单次交互记忆值(按式(7)或式(10)计算)与所交互节点的影响力大小(由节点的度来衡量)成正比、与节点间观点差值成反比。考虑到每当对某事件的记忆值达到记忆阈值时,一些个体每次都会立即对自身观点进行更新,而有些“顽固”个体会继续沿用原观点而一次也不进行观点更新的实际情况,考虑将所有个体可能的观点更新次数平均,并以此作为每个个体能够进行观点更新的次数上限(即观点更新的次数阈值,记为Ct)。并令C(i,t)表示若在t时刻节点i的记忆值达到记忆阈值,该节点已经经历观点更新的次数。

在节点交互过程中,需比较i和j的观点值。若两节点的观点差值不大于置信值d,即ΔOij(t)= |-Oj(t)|≤d,则i,j根据式(3)进行观点更新。当两节点的观点差值大于置信值 d,即 ΔOij(t)= |Oi(t)-Oj(t)|＞d,考虑到实际情况(虽然多数人可能不会立即改变自己的观点,但是在经历多次观点冲突并形成深刻记忆后,个体可能会动摇或改变自身观点),对以下2种情况进行分析:

(1)当节点i的记忆值达到记忆阈值,且该节点在t时刻的观点更新次数C(i,t)未达到Ct;此时节点j进行记忆值叠加更新。即当|M(i,t)|≥Mt, C(i,t)＜Ct时,节点i根据式(3)式进行观点更新,同时按式(5)将节点i的记忆值重新初始化为0,并根据式(6)更新观点更新次数:

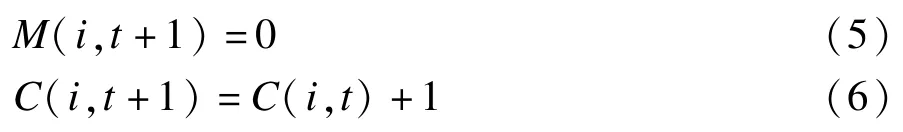
对于节点j记忆值的更新过程,按照1)和2)加以分析:

1)若O(j,t)＜O(i,t),则节点j产生的单次交互记忆值M1(j,1)为正记忆值,单次交互记忆值M1(j,1)可按式(7)计算,同时节点j根据式(8)更新记忆值:

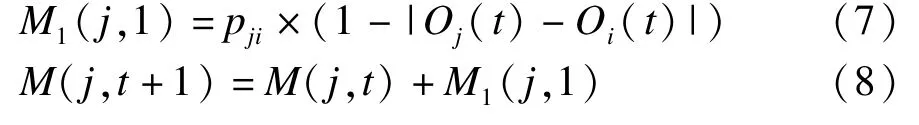
2)若O(j,t)＞O(i,t),则节点j产生的单次交互记忆值M2(j,1)为负记忆值,即单次交互记忆值M2(j, 1)=-M1(j,1),节点j可根据式(9)更新记忆值:

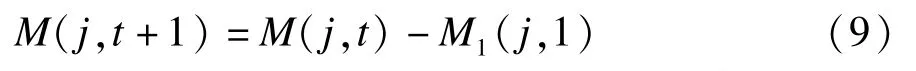
(2)当节点i的记忆值未达到记忆阈值时,即当|M(i,t)|＜Mt时,两节点继续进行记忆的叠加更新,同时两节点的观点值保持不变。节点j根据自身观点值大小情况按照式(8)或式(9)更新记忆值,节点i记忆值更新与第(1)种情况中节点j记忆值更新过程类似,即可分为1)和2)进行讨论:

1)若O(i,t)＜O(j,t),则节点i产生的单次交互记忆值M1(i,1)为正记忆值,单次交互记忆值M1(i,1)按式(10)计算,同时节点i根据式(11)更新记忆值:

2)若O(i,t)＞O(j,t),则节点i产生的单次交互记忆值M2(i,1)为负记忆值,即单次交互记忆值M2(i,1)=-M1(i,1),节点i根据式(12)更新记忆值:

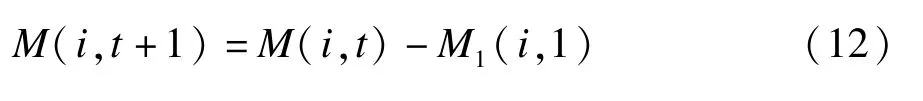
3 实验结果及分析

本文分别在ER［17］,BA［18］和Facebook(http:// www.datatang.com/data/1605)网络中进行模型的仿真实验。ER,BA和Facebook网络基本情况:节点总数均为N=769;ER网络节点平均度k=43.00,最大度数为80,次大度数为75;BA网络节点平均度k=42.56,最大度数为 186,次大度数为 180; Facebook网络节点平均度k=43.30,节点最大度数为248,次大度数为203。

3.1 优先选择与记忆效应对网络一致性观点影响

首先在ER,BA和Facebook网络中,对于基本Deffuant模型,分别采用随机选择策略和优先选择策略(将基本Deffuant模型中的随机选择策略改为优先选择策略),随着置信值d的变化,考察网络中节点观点最终状态。图1横坐标表示置信值d,纵坐标表示终态时网络中最大群节点密度。

图1 采用不同选择策略的网络观点最终状态

由图1可知,随着置信值d的增加,2种交互策略作用下网络最终的最大群规模的变化趋势一致。当置信值0＜d＜0.3时,网络中各节点观点难以统一,网络终态为多组群,各节点观点难以收敛于一致观点;当置信值0.3＜d＜0.5时,网络终态时最大群规模增大,各节点趋向于达成一致观点;在d≥0.5时,网络基本达成一致观点。总得来说,在网络不考虑节点的记忆效应,即使选用优先选择策略,其一致性观点的形成仍然依赖于d的取值。

下面考察记忆效应的加入对网络观点演化的影响。图2表示ER,BA和Facebook网络在选用不同选择策略的情况下,各节点的观点值的演化情况。图中纵坐标表示网络中节点的观点值。参数设置为:记忆阈值Mt=0.2,置信值d=0.15,观点更新次数阈值Ct=3。

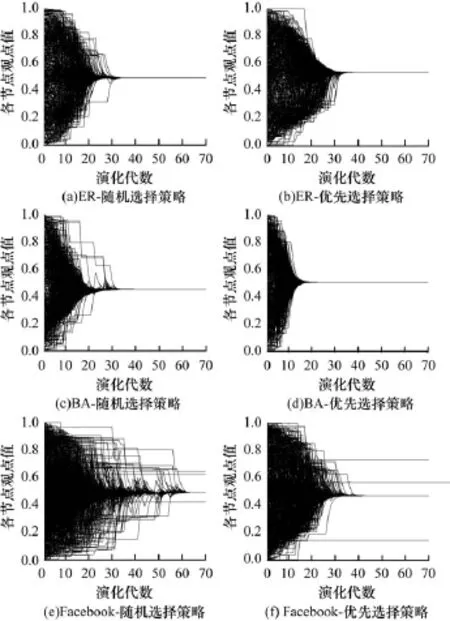
图2 不同选择策略作用下3种网络中的节点观点演化

从图2可以看出,当d=0.15时,ER和BA网络中所有节点达成一致观点;但由图1可知,当d= 0.15时,在不考虑节点记忆效应的情况下,ER和BA网络不能达成一致观点。由此可见,记忆效应的加入有效地驱使了网络达成统一观点。此外,在Facebook网络中,网络不能形成一致观点。这是因为Facebook不是连通的网络,网络中存在着几组孤立群,致使网络不能达成一致观点。

继续在Facebook网络中考察最大群(网络最大连通图)中各节点的观点值的演化情况,如图3所示。其中,仿真参数设置见图2。

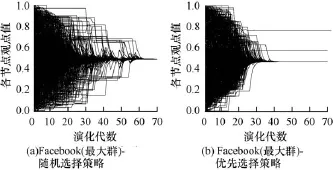
图3 Facebook网络中最大群中的节点观点演化

对比图2(c)、图2(d)和图3可知,在非均匀网络中(BA和Facebook)采用优先选择策略相比于采用随机选择策略而言,能更快地使网络达成一致观点。原因是与随机选择策略相比,优先选择策略使得节点选择度大的节点作为交互节点的概率增大。在BA和Facebook网络中,网络的度分布呈现较为明显的非均匀分布。节点与度大的节点进行高频度的交互有效地促进了度大节点的观点在网络中的快速传播,这有助于网络达成一致观点。因此优先选择策略能够有效地促进非均匀网络达到一致观点。

考虑到优先选择策略有助于网络达成一致观点,下面将采用优先选择策略作为网络的交互策略进行实验。此外,Facebook网络中的最大群将被选择以进行进一步的实验。

3.2 Ct,d,Mt对网络达成一致观点的影响

首先分析观点更新次数阈值Ct对网络观点演化的影响。图4为3种网络中所有节点的观点值的演化情况。参数设置为:记忆阈值Mt=0.2,置信值d=0.15,观点更新次数阈值Ct=2。

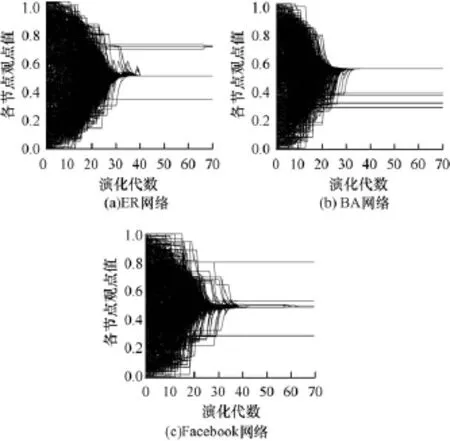
图4 3种网络中的节点观点演化

由图4可知,当3个网络的观点更新次数阈值Ct均设置为2时,网络不能形成一致观点。对比图2(c)、图2(d)以及图3(b)可以得出,Ct对网络的观点形成有一定的影响。这是因为给定网络置信值时,当Ct越小,节点在记忆值达到记忆阈值时进行观点更新的机会越少,而这不利于网络达成一致观点。

图5表示当记忆阈值Mt为固定值时(Mt= 0.2),3个网络随着置信值d的变化,网络达到一致观点所需设置的最小(临界)观点更新次数阈值Ct以及所需的演化代数t。

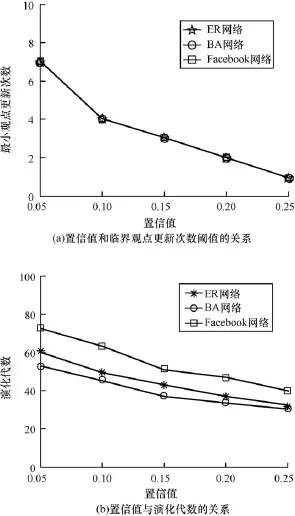
图5 最小观点更新次数阈值和所需的演化代数

从图5(a)可以看出,随着置信值d的增加,3个网络达成一致观点所需设置的最小观点更新次数阈值Ct值均逐渐减少。这是因为网络的置信值越大会使得网络中直接进行观点更新的节点越多,这减少了节点通过记忆累加的方式实现观点更新的机会,从而Ct也相应地减少。从图5(b)可以看出,在给定记忆阈值Mt条件下,3个网络在置信值d取值较小时均能达成一致观点。对比图1(b)的实验结果可以得出:在本文提出的新的观点动力学模型中,记忆效应不仅能够促进网络观点达成一致,而且在置信值很小的情况下,也能使得网络达成一致观点。

此外,对比图5(a)和图5(b)可以看出,对于某一d取值,虽然3个网络达成一致观点所需设置的最小观点更新次数阈值一样,但各网络所需的演化代数不一样。这是因为3个网络初始的观点分布是随机均匀分布的,对于给定的置信值d,当各网络中的节点在置信值d之内进行观点更新后,网络达到一致观点所需设置的最小观点更新次数阈值Ct是一致的。

图6表示当d和Ct固定时(d=0.15,Ct=3),在不同记忆阈值Mt条件下,3个网络达成一致观点所需的演化代数t。

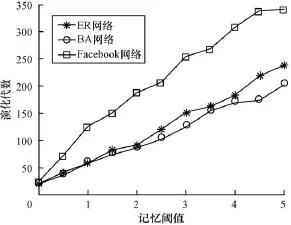
图6 在不同记忆阈值Mt条件下3个网络达成一致观点所需演化代数

从图6可知,当d和Ct固定时,对于不同的记忆阈值,3个网络的观点最终都能趋于一致,但网络收敛的演化代数t随记忆阈值Mt的增大而增大。

此外,从图6也可看出,BA网络比ER网络能更快的达到一致观点状态,这进一步验证得到的结论:网络采用优先选择策略可加快非均匀网络形成一致观点的时间。仿真结果也表明,Facebook网络观点达成一致所需时间最长。考虑其原因为: Facebook网络中各节点度大小相差悬殊,节点进行记忆更新时,中小度数的节点产生单次交互记忆值较小,致使节点记忆值的累加速度慢,延缓了节点观点的更新以及网络一致观点的收敛。

4 结束语

本文提出一个新的观点动力学模型,考虑了优先选择和记忆效应因子,并分别在ER,BA和真实Facebook网络中进行实验,分析2个因子对网络达成一致观点的影响。仿真结果表明:优先选择策略促进了非均匀网络收敛于一致观点;记忆效应的加入不仅能够促进网络达成一致观点,而且在置信值很小的情况下,也能使得网络达成统一观点。原因是优先选择策略使得节点与度大的节点交互的机会变多,有效地促进了度大的节点的观点在网络中快速传播,从而有助于网络达成一致性观点状态。但是即使选用优先选择策略,若不考虑节点记忆效应,网络一致性观点的形成仍然依赖于置信值的取值。记忆效应的加入使得在节点间观点差值大于置信值时,节点可通过多次记忆值累加直至突破记忆阈值Mt的方式进行有限次观点更新,从而促进了网络一致性观点的形成。

［1］ 李 翔.复杂动态网络传播动力学［J］.力学进展, 2008,38(6):723-732.

［2］ 刘 云,丁 飞,张振江.舆论形成和演进模型的研究综述［J］.北京交通大学学报:自然科学版,2010,34 (5):83-88.

［3］ 熊 熙,胡 勇.基于社交网络的观点传播动力学研究［J］.物理学报,2012,61(15):104-110.

［4］ Krawiecki A,Hołyst J A,Helbing D.Volatility Clustering and Scaling for Financial Time Series Due to Attractor Bubbling［J］.Physical Review Letters,2002,89(15).

［5］ Krapivsky P L.Kinetics of Monomer-monomer Surface Catalytic Reactions［J］.Physical Review A,1992, 45(2):1067.

［6］ Sood V,RednerS.VoterModelon Heterogeneous Graphs［J］.Physical Review Letters,2005,94(17).

［7］ Galam S.Minority Opinion Spreading in Random Geometry［J］.TheEuropean PhysicalJournalBCondensed Matter and Complex System,2002,25(4): 403-406.

［8］ Krapivsky P L,Redner S.Dynamics of Majority Rule in Two-state Interacting Spin Systems［J］.Physical Review Letters,2003,90(23).

［9］ Slanina F,Lavicka H.Analytical Results for the Sznajd Model of Opinion Formation［J］.The European Physical Journal B-Condensed Matter and Complex System, 2003,35(2):279-288.

［10］ Deffuant G,Neau D,Amblard F,et al.Mixing Beliefs Among Interacting Agents［J］.Advances in Complex Systems,2000,3(1):87-98.

［11］ Hegselmann R,Krause U.Opinion Dynamics and Bounded Confidence Models,Analysis,and Simulation［J］.Journal of Artificial Societies and Social Simulation,2002,5(3):216-219.

［12］ Yang H X,Wang W X,Lai Y C,et al.Convergence to GlobalConsensusin Opinion DynamicsUndera Nonlinear Voter Model［J］.Physics Letters A,2012, 376(4):282-285.

［13］ Nardini C,Kozma B,Barrat A.Who's Talking First? Consensus or Lack Thereof in Coevolving Opinion Formation Models［J］.Physical Review Letters,2008, 100(15).

［14］ Kozma B,Barrat A.Consensus Formation on Adaptive Networks［J］.Physical Review E,2008,77(1).

［15］ Grauwin S,Jensen P.Opinion Groups Formation and Dynamics:StructuresThatLastfrom NonLasting Entities［J］.Physical Review E,2012,85(6).

［16］ 宋冰冰,王海艳.马太效应综述［J］.社会心理科学, 2005,20(1):11-12.

［17］ Erdös P,Rényi A.On Random Graphs I［J］.Publicationes Mathematicae Debrecen,1959,6:290-297.

［18］ Albert R,Barabási A L.Statistical Mechanics of Com-plex Networks［J］.Reviews of Modern Physics,2002,74(1):47.

编辑 索书志

Research on Opinion Dynamics Based on Priority Selection and Memory Effect

HUANG Qinghua,SONG Yurong
(College of Automation,Nanjing University of Posts and Telecommunications,Nanjing 210046,China)

Opinions sharing or reaching consensus is a common social phenomenon.In consideration of the facts that nodes prefer to select certain nodes to communicate and they have memory for viewpoints which are different from their own,this paper tries to establish a novel opinion dynamics model by extending the Deffuant model.Priority selection strategy and the memory effect of node are adopted in the model.And it studies the influences of these two factors on network opinion formation.Experimental results show that the proposed model adopting priority selection strategy helps consensus formation in non-uniform network.But when the network adopts the priority selection strategy without considering memory effect,the formation of consensus still depends on threshold.And the joining of the memory effect not only can promote formation of network consensus,but also can make the network reach consensus at a small threshold.Research results show that with the increasing of the threshold,the smallest opinion updating time threshold to reach consensus decreases.

Deffuant model;priority selection;memory effect;opinion dynamics;non-uniform network

1000-3428(2014)11-0036-06

A

TP393

10.3969/j.issn.1000-3428.2014.11.007

国家自然科学基金资助项目(61373136);教育部人文社科规划基金资助项目(12YJAZH120);江苏省"六大人才高峰"基金资助项目(RLD201212)。

黄庆花(1988-),女,硕士研究生,主研方向:复杂网络;宋玉蓉,教授。

2013-11-29

2014-01-02E-mail:huangqinghua0525@163.com

中文引用格式:黄庆花,宋玉蓉.基于优先选择和记忆效应的观点动力学研究［J］.计算机工程,2014,40(11):36-41.

英文引用格式:Huang Qinghua,Song Yurong.Research on Opinion Dynamics Based on Priority Selection and Memory Effect［J］.Computer Engineering,2014,40(11):36-41.