基于虚拟现实技术的测量数据可视化方法
周 鑫, 方 宏, 侯立新, 刘 科, 赵海宁,安 莹, 杨 丽, 卞 昕
(1.中国计量科学研究院信息计量室,北京 100029;
2.北京市西城区药品检验所,北京 100037)
基于虚拟现实技术的测量数据可视化方法
周 鑫1, 方 宏1, 侯立新1, 刘 科1, 赵海宁1,安 莹2, 杨 丽1, 卞 昕1
(1.中国计量科学研究院信息计量室,北京 100029;
2.北京市西城区药品检验所,北京 100037)
在从数据可视化的角度对测量数据进行分类的基础上,对两种重要类型的测量数据给出了三维建模方法。然后利用CAVE技术和3D技术,结合以映射、绘制为主线的数据可视化基本流程,提出了一种具有沉浸感和立体感的通用型测量数据可视化方案。技术方案以建立三维模型为基础,以对视图的控制为核心,以场景设置为辅助,实现并验证了测量数据可视化。
计量学;数据可视化;虚拟现实;CAVE;三维建模
1 引 言
随着各个学科的发展,需要测量的参数越来越复杂,测量结果的数据量也越来越大。单纯通过文本或简单图表已经无法有效表达这些海量的复杂数据。将这些测量数据可视化,使测量数据直观呈现在数据分析者眼前,利用人类的视觉系统来辅助分析、解释数据,是一种十分必要、有效的数据探索手段。测量数据可视化的另外一个重要作用体现在:数据可视化技术是实现虚拟测量的基础,而虚拟测量则是利用现代信息技术辅助传统计量的重要研究方向。
因为测量数据可视化重要性日益显现,国际上已有一些先进国家的测量机构成立了专门完成数据可视化的工作组,比如美国国家标准与技术研究院(NIST)成立了名为“Scientific Applications and Visualization Group”的工作组。该工作组为NIST各专业部门提供数据可视化服务,文献[1~4]展示了NIST通过数据可视化加速科学研究的工作成果。在国内,对可视化的研究正逐渐受到重视,目前应用较多的领域有可视人体、分布式虚拟风洞、三维医学影像重建、城市模型可视化等[5]。针对测量数据的可视化在国内还是一个新兴概念,还未发现专门介绍测量数据可视化的文献。
本文首先从数据可视化的角度对测量数据进行分类,基于此分类,通过虚拟现实技术实现了一套测量数据可视化的方法和系统。本方法有别于常见的应用于某一特定领域、针对某种特定数据的可视化方法。本方法具有较强的通用性,适用于各个领域多种类型的测量数据。目前,应用本方法已实现了对长度测量数据、电场测量数据、通信信号质量测量数据的可视化。本方法使用的虚拟现实技术是一门综合性的信息技术,融合了多个计算机技术分支的最新发展成果。为了实现测量数据的可视化,主要采用了虚拟现实技术中的CAVE技术和3D技术。其中,3D技术是一种相对成熟的技术,本文不做详细介绍,仅对CAVE技术做简要介绍。同时,由于测量数据的应用领域广泛,其数据结构、数据属性千差万别,为了增强可视化系统的通用性,首先从可视化的角度对测量数据进行分类。
2 相关工作
2.1 测量数据分类
首先,把各类测量数据都抽象为Y=f(X)这样一个函数关系。表达式中的Y代表测量结果也就是可视化对象。表达式中X对应测量结果Y发生的条件,如测量的空间位置,测量的时间等任何和Y相关的可数字化的量。把Y的维数称为测量结果的维数,X的维数称为测量条件的维数。这样根据X和Y维数的不同,对数据分类。比如,最简单的数据类型是X、Y的维数都为1的情况。常见的使用示波器显示的信号时域图就属于对这种类型数据的可视化,即Y对应被测量信号在某个时刻的幅值,X对应该测量发生的时间。当X和Y的维数都较小(X、Y的维数均小于3)时,数据可视化图形绘制的方法比较简单也比较成熟,本文不做详细介绍。当X或Y的维数大于3时,一般采取降维方式先处理数据,即提取数据中的部分信息使X和Y的维数都小于或等于3,从而按照低维数据的可视化方式给予显示。本文重点在于介绍X的维数为3时测量数据的可视化方式。为行文方便,当X的维数为3、Y的维数为1时,此类数据简称为三维标量数据,其中三维是指X的维数为3,标量表示测量对象Y的维数为1。X的维数为3,Y的维数大于1时,称为三维矢量数据。以上两种数据又统称为三维数据。在测量数据可视化的技术方案中,将根据不同的数据类型建立相应的三维模型,建模方法在第4节中做详细介绍。
2.2 CAVE技术
CAVE是洞穴式显示装置(Computer Automatic Virtual Environment)的简称,是指一种基于计算机图形学的多面式投影显示系统[6]。由于CAVE系统实现了多面式投影,并且多个投影面之间是两两垂直的,因此有效增加了观察者的视野范围,增强了观察者的沉浸感以及图像的空间感,从而有利于表达图形的空间深度信息。这些特性在表达大量三维数据的空间位置关系时可起到显著作用。CAVE系统的关键在于保证各投影面的图形拼接自然连续,根据文献[6]的介绍,通过对视图中投影变换矩阵的控制可以使投影面拼接自然连续。所谓投影变换矩阵是指将三维模型投影到显示设备的二维平面上时,将三维坐标(即三维模型在三维空间中的坐标)转变为二维坐标(即在显示屏幕上的坐标,因显示屏幕为二维所以需将三维模型的三维坐标转换为二维坐标)所经过的矩阵变换。矩阵变换以齐次坐标形式完成。在CAVE系统中,一个投影面所对应的投影变换矩阵如式(1)所示。

式中,D为投影面边长的一半,ZFar和ZNear是投影远近深度距离,x、y、z则是视点的位置。对于其他各投影面来说,对CAVE用户坐标系进行90度旋转后,即可得出相应的投影变换矩阵。
3 技术方案
图1是测量数据可视化系统的技术方案图。
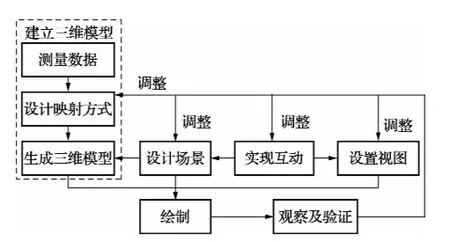
图1 测量数据可视化技术方案图
首先从整体上看,本技术方案虚线框中部分的作用是建立表达数据的三维模型。它首先根据数据类型确立一种映射方式,然后按照此映射方式将测量数据转化为三维模型。不同类型的三维数据使用不同的映射方式,采用不同的三维建模方法。这部分工作是数据可视化工作的主体,将在本文系统实现部分详细介绍三维标量及三维矢量数据的映射和建模方法。
技术方案中的“设计场景”包括对光照方式、用于互动的按钮或控件、实物模型等部件的设置与控制。实物模型是指可视化图形中不表示数据的用于表示真实物体的三维模型。例如,在电磁场可视化的工作中,电磁场领域的测量专家要求在可视化图形中加入代表天线的模型,以便于他们可以根据天线的位置和方向理解电磁场的测量数据。由于天线模型本身不表示数据,而是一个实物,因此归纳为实物模型,起到帮助观察者理解数据的目的。
技术方案中的“实现互动”本质上是一种人机交互技术。桌面型系统的人机交互手段通常是通过键盘和鼠标,但这种交互方式缺乏现实感,减弱了CAVE系统所营造的沉浸感。为增强现实感使观察者以一种接近自然的方式进行交互,可以利用数据手套、位置跟踪器等产品实现交互[7]。结合技术方案图,“实现互动”实际上是利用各种传感设备,获得观察者的各种动作信息,并根据这些动作信息改变视图和场景的设置。
技术方案中的“设置视图”是实现立体效果和沉浸效果的核心。立体效果是通过3D技术实现的。而3D技术的核心在于为观察者的双眼各设置一个视图,并通过设置两个视图间的视差来实现立体效果。根据前文关于CAVE技术的原理简要介绍,通过设置视图中的投影变换矩阵实现沉浸效果。同时利用视图还可以设定用户观察场景的观察位置、视线方向、视野范围以及裁剪面参数等。
技术方案中的“绘制”是数据可视化基本流程的步骤之一,在本技术方案中绘制是根据视图的设置将三维模型及场景转换成要显示的二维图像元素。
技术方案中的“观察及验证”是指可视化人员观察并验证绘制出来的图像,并对各个步骤进行调整以达到更好的可视化效果。在测量数据可视化领域通常从以下几个方面验证可视化图形的正确性[8]:
(1)图形中图形元素幅度的大小顺序是否正确;
(2)一些标志性的关键点处的图形是否正确;
(3)边界、角落处是否正确;
(4)零值、最大最小值是否出现在正确的位置;
(5)渐近线是否正确。
另外,如果可以用不同方式生成同一数据的可视化图形,并比较所生成的可视化图形是否一致,也是对可视化图形进行验证的有效方法,这种方法简称为比较法。最后,结合测量领域的特点,我们认为数据可视化的目的在于直观快速地为数据分析者提供一种对数据定性的认识,而在测量领域通常都需要做精准的定量分析。因此,通常来说都会使用数值分析方法,验证由图形得来的对数据的定性认识或预测是否正确。这种基于数值分析的判断也是对测量数据可视化图形的验证方法之一。
4 系统实现
对应技术方案中的各个步骤,其中“建立三维模型”使用VRML语言实现,“设计场景”、“实现互动”、“设置视图”、“绘制”均通过EON软件实现。如第3节所述"设置视图"是实现立体感和沉浸感的核心,本节将对视图的设置方法做详细介绍。
“设置视图”通过EON软件完成,EON是一款完全基于GUI(Graphical User Interface,图形用户界面)用来研发实时3D多媒体应用程序的设计工具。在EON中通过Viewport(视点)节点来完成对视图的设置。
首先为了实现立体显示,需要设置左眼和右眼视图的视差。在Viewport节点上设置StereoMaxParallax(立体最大视差)参数可调整左右眼的视差。StereoMaxParallax参数为0时即没有视差无立体效果,随着StereoMaxParallax的增大立体效果逐渐增强。如果StereoMaxParallax参数设置过大,人脑将无法融合左右眼看到的两幅图像,从而使观察者感到眩晕,影响可视化效果。通常StereoMaxParallax参数设置为20左右,根据观察者人体特征及显示设备的不同,需调节StereoMaxParallax参数值以达到更好的观察效果。实现立体效果的本质是生成两幅具有一定视差的视图,但是由于这两幅视图具有很强的相关性,因此在EON中,使用一个Viewport节点来实现这两幅视图,从而简化了程序设计。
结合本文第2节的介绍,CAVE技术的关键是对投影变换矩阵的设置,在Viewport节点上通过设置ProjectionTransform(投影变换矩阵)参数来实现对投影变换矩阵的设置。ProjectionTransform参数是一个包含16个元素的数组,对应投影变换矩阵中的16个元素。从式(1)可以看到,投影变换矩阵与视点的位置相关。如果要实现观察者走动时,在各个位置都能看到正确的多面式投影图像,则必须使用一定的互动设备(如三维头部跟踪器)确定观察者眼睛所处位置,并将此位置信息传递给EON软件,EON软件可通过其Script(脚本)节点实现投影变换矩阵中的算法,从而实现对ProjectionTransform参数的实时设置。
5 实验及结果分析
5.1 实验环境及效果
实验的硬件环境为:Intel Core2 Duo 3 GHz CPU,4 GB内存,Nvidia Quadro FX1700显卡,NVIDIA 3D Vision P854立体眼镜。软件环境为:Windows XP操作系统,EON Studio 7.0.0编程环境,VRML2.0建模语言,DirectX10图形程序。
下面以电场数据为例,说明本可视化系统的实现效果及可视化结果的验证方法。电场数据是典型的三维矢量数据。被测量电场本身是一个矢量,电场数据包括测量点的位置信息x、y、z以及该位置上电场在x、y、z三个方向上的分量ex、ey、ez。即对应每一个测量点有三维矢量数据(x、y、z、ex、ey、ez)。根据第4节介绍的三维矢量数据的建模方法,使用彩色圆锥表达数据。按照本文介绍的技术方案,搭建了一个两面式的CAVE系统,可视化效果如图2、图3所示。在对1万多个圆锥的场景进行测试中系统运行顺畅,几乎感觉不到延迟感,各投影面均能提供正确的立体影像,各投影面的拼接自然,连续感强。
5.2 实验结果验证
前文已简要介绍了验证测量数据可视化图形的方法,下面将结合本实验,重点介绍比较法。

图2 包含观察者在内的系统运行效果图

图3 两面式CAVE系统运行效果图
因为可视化系统是以软件算法为核心的。因此,在比较法中所谓以其它方式实现同一数据的可视化,其核心在于使用不同软件实现同一数据的可视化。本实验使用FEKO软件生成相同数据的电场图形,从而验证本课题研制系统的正确性。FEKO是一款著名的用于三维结构电磁场分析的仿真工具。为便于观察比较图形,截取了x=-5、x=0.1、z=-5三个截面,并调整了观察视角。所得对比图形如图4~图9所示。其中,图4~图6为本课题所研制可视化系统生成的图形。图7~图9为FEKO软件生成的图形。图10摘自介绍电磁场理论的经典教科书《天线》[4]。该图截取了x=0.1附近的电场图。可以看出这3种方式得到的图形,从幅度和方向上所描述的信息都是一致的。通过以上方式对本实验数据可视化图形进行了验证。
6 结 论

图4 NIM(x=0.1)电磁场截面图

图5 NIM(x=-5)电磁场截面图

图6 NIM(z=-5)电磁场截面图
本文首先从数据可视化的角度给测量数据提供了一种分类方法。对测量数据的合理分类将大大增强可视化方法的通用性。在此分类的基础上,按照本文介绍的技术方案搭建了一套具有沉浸感和立体感的多面式测量数据可视化系统。最后结合实例说明了对可视化结果的验证方法。通过上述步骤,形成了一套从数据分析开始至图形验证结束的较为系统完整的通用型测量数据可视化方案。

图7 FEKO(x=0.1)电磁场截面图
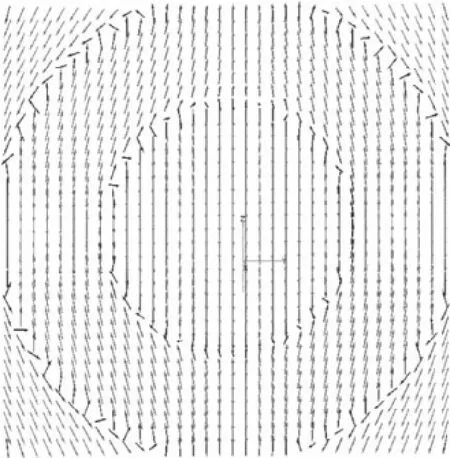
图8 FEKO(x=-5)电磁场截面图

图9 FEKO(z=-5)电磁场截面图
测量数据可视化是虚拟测量的基础,而虚拟测量则是利用现代信息技术辅助传统计量的重要发展方向。围绕虚拟测量技术,测量数据可视化未来工作的重点包括:
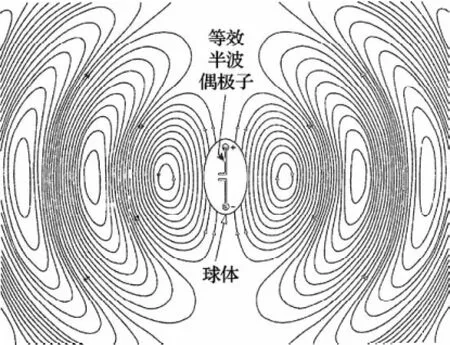
图10 《天线》(x=0.1)电磁场截面图
(1)增强实时性:即在进行测量的同时,实时地对测量数据实现可视化。这需要对网络技术、并行计算等技术的理解和运用。实现实时显示后,可以通过得到的图形实时指导测试过程和测试方法。
(2)增强交互性:在实现实时性的基础上,实现虚拟现实世界中互动操作到真实世界实际测量动作的映射。测量人员通过在虚拟现实世界中的一些动作实现对测试装置的设置从而控制真实世界的测量,并将测量结果实时显示出来。
(3)加强标准化工作,实现标准数据可视化流程和标准可视化场景模型,以增强系统的通用性和易用性。
致谢:感谢中国计量科学院信息电子所、长度所的大力支持,信息电子所孟东林、李潇,长度所薛梓研究员为实验提供了大量测量数据,并对可视化效果给出了评价和宝贵的改进意见。
[1] Sims JS,George W L,Griffin T J,et al.Accelerating Scientific Discovery Through Computation and Visualization III.Tight-Binding Wave Functions for Quantum Dots[J].Journal of Research of the National Institute of Standards and Technology,2008,113(3):131-142.
[2] Sims J S,Hagedorn J G,Ketcham P M,et al. Accelerating scientific discovery through computation and visualization[J].NIST Journal of Research,2000,1(105):875-894.
[3] Sims J S,George W L,Satterfield S G,et al. Accelerating scientific discovery through computation and visualization II[J].Journal of Research of the National Institute of Standards and Technology,2002,107(3):223-245.
[4] 克劳斯,马赫弗卡.天线[M].章文勋,译.北京:电子工业出版社,2004,29-31.
[5] 唐伏良,张向明,茅及愚,等.科学计算可视化的研究现状和发展趋势[J].计算机应用,1997,17(3):8-10.
[6] 林柏纬,潘志庚,杨建,等.基于PC架构的高性能CAVE系统[J].计算机辅助设计与图形学学报,2003,15(6):724-729.
[7] 胡小强.虚拟现实技术基础与应用[M].北京:北京邮电大学出版社,2009,22-50.
[8] John Gilby,Jeremy Walton.Software Support for Metrology good practice guide No.13:data visualisation[R].NPL Report DEM-ES 009,2006.
Visualization of Measurement Data Based on Virtual Reality
ZHOU Xin1, FANG Hong1, HOU Li-xin1, LIU Ke1, ZHAO Hai-ning1,AN Ying2, YANG Li1, Bian Xin1
(1.Information Metrology Laboratory,National Institute of Metrology,Beijing 100029,China;
2.Beijing Xicheng Institute for Drug Control,Beijing 100037,China)
Based on the classification of measurement data from the perspective of visualization,a method of 3D modeling for two types ofmeasurement data is presented.Then by integrating the CAVE and 3D technologies into the basic procedure of data visualization,a new technical solution formeasurement data visualization is proposed.The solutionwhich has a 3-D effect and an immersion effect to enhance the perception of observers,is based on 3D modeling,assisted by scene setup,and uses view control as the essential part.
Metrology;Data visualization;Virtual reality;CAVE;3Dmodel
TB973
A
1000-1158(2014)04-0387-06
2012-11-06;
2013-07-23
中国计量科学研究院基本科研业务费项目(27-AKY1139)
周鑫(1980-),男,北京人,中国计量科学研究院助理研究员,主要从事信息计量研究。zhouxin@nim.ac.cn

