斜变滤波器频域加窗对图像重建的影响
乔志伟
(中北大学电子与计算机科学技术学院,山西太原 030051)
斜变滤波器频域加窗对图像重建的影响
乔志伟
(中北大学电子与计算机科学技术学院,山西太原 030051)
斜变滤波器的性能对图像重建有重要的影响,频域加窗设计法是其主要的设计方法。设计了4种经典的加窗滤波器:RL滤波器、SL滤波器、Hamming窗滤波器和指数窗滤波器。从单位冲激响应和频率响应2个方面分析了这4种滤波器的特性;从频率响应和旁瓣衰减速度2个方面比较了这4种滤波器。理论分析与仿真结果表明:指数窗滤波器的震荡噪声最小;SL滤波器整体最优。
计量学;斜变滤波器;窗函数;图像重建;滤波反投影算法;频率响应
1 引 言
CT(Computed Tomography)又称为计算机断层成像技术,是当今最好的无损检测方法之一,已经被广泛应用到了医学、工业、地震学和考古学等领域[1~3]。
X射线工业CT算法分为解析式算法和迭代式算法2种,其中解析式算法居于优势地位。按照成像的维度分,解析式重建算法分为二维CT算法和三维CT算法,二维算法的典型代表是滤波反投影(filtered back projection,FBP)算法,而三维算法的典型代表是FDK算法。可以认为,FDK算法是一种近似的滤波反投影算法。研究影响此类算法的各种因素时,通常以FBP算法为研究对象[4]。
影响FBP算法的因素较多,其中斜变滤波器的性能是非常重要的一个因素。常用的RL滤波器是斜变滤波器的频率响应加矩形窗形成的;SL滤波器是加“sinc”窗形成的。可见,给斜变滤波器的频率响应加窗是斜变滤波器设计的一种基本方法[5~7]。由信号处理理论可知,矩形窗、三角窗、升余弦类窗各有其特点,因此有必要系统研究各种窗函数对图像重建的影响。
本文将从单位脉冲响应及频率响应等角度设计并分析各种滤波器。在比较几种滤波器时,将从窗函数波形、频率响应波形、单位冲激响应的旁瓣衰减速度等方面展开理论研究。同时,通过仿真实验,客观比较窗函数对重建的影响,并给出理论解释。
2 RL滤波器(加矩形窗)
RL滤波器是最常用的斜变滤波器,它是通过加矩形窗形成的。
理想斜变滤波器的频率响应为

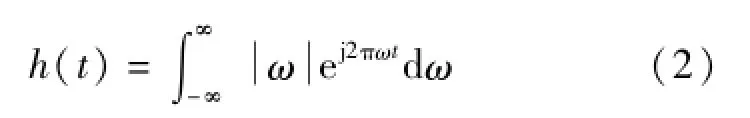
连续状态的单位冲激响应为加矩形窗的RL滤波器的频率响应为

根据冲激响应不变法的原理,对其用d采样,可以得到离散状态下的滤波器的单位脉冲响应

设d=1,采集-50~50共101个点,h(n)的波形见图1。
由图可以看出,该信号是一个实偶信号,在中心点0处有最大值,向两边呈振荡式展开,幅值迅速衰减,并且在奇数点处的值均为负数。
图2为图1所示的斜变滤波器的频率响应。
该滤波器能较好地重建图像,但其有明显的振荡噪声。
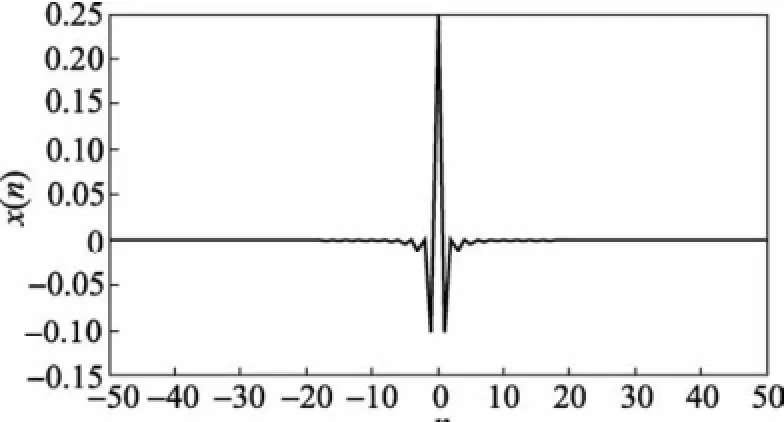
图1 RL滤波器h(n)的波形
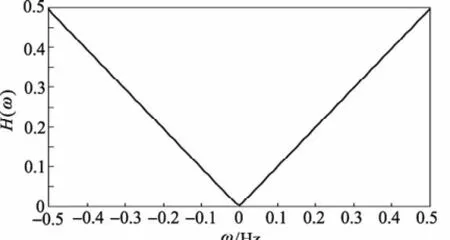
图2 RL滤波器的频率响应
3 SL滤波器(加sinc窗)

设d=1,采集-50~50共101个点,hS-L(n)的波形见图3。
图4为SL滤波器的频率响应,由图可以看出,在最高频率附近,幅度被压低,有效减小了Gibbs效应,可以抑制高频噪声。但其频率响应在“0”处的值不为0,这将引起CT图像的CT数(强度)的整体下降。
4 加海明(Hamming)窗

图3 SL滤波器的单位脉冲响应hS-L(n)的波形
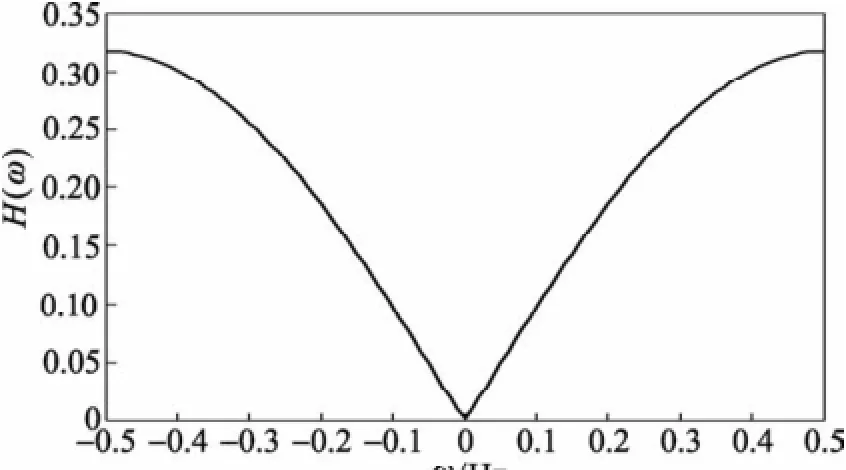
图4 SL滤波器的频率响应
海明窗是一种改进的升余弦窗,依据经典的信号处理理论关于FIR滤波器加离散海明窗的原理,可设计出给连续状态的斜变滤波器频率响应加窗的海明窗。
加海明窗的斜变滤波器的频率特性为

设d=1,采集-50~50共101个点,hH-M(n)的波形见图5,该滤波器的频率响应见图6。
可以看出,大约在最高频率的1/2处,幅度响应达到最大值,在带宽的前半部分,基本呈现斜变特征(单调上升);但在带宽的后半部分,其幅度响应平滑地下降,到最高频率处,幅度响应被“压低”到很低(0.04)。该滤波器可以较好地减少Gibbs效应,可以抑制高频噪声。该滤波器在“0”处的值仍然不为0,会引起重建图像强度的整体下降。
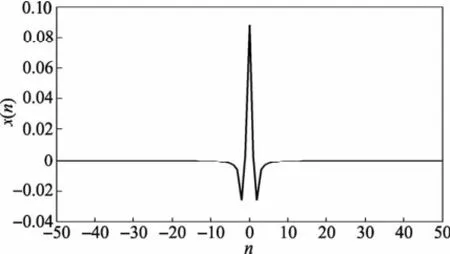
图5 海明窗斜变滤波器的单位脉冲响应
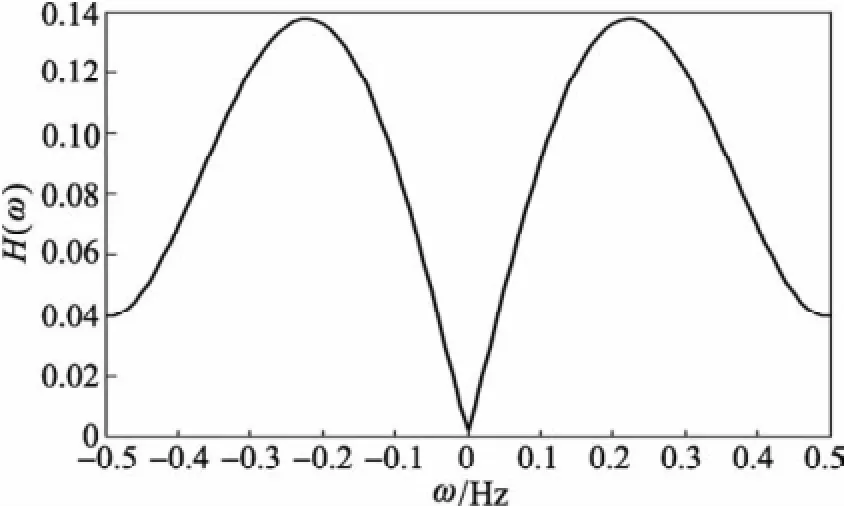
图6 海明窗斜变滤波器的频率响应
5 加指数型窗函数
2004年,范惠荣和徐茂林等人提出的指数型窗函数滤波器的频率响应为[8~10]

hZ-S(0)的确定比较复杂,一般采用数值积分的方法来求取,而不采用解析法,因式(16)所示的积分太过复杂,很难求得解析解。
根据傅里叶反变换公式,可知

式(15)和式(16)即为指数型窗函数的单位脉冲响应。
设d=1,采集-50~50共101个点,hZ-S(n)的波形见图7。
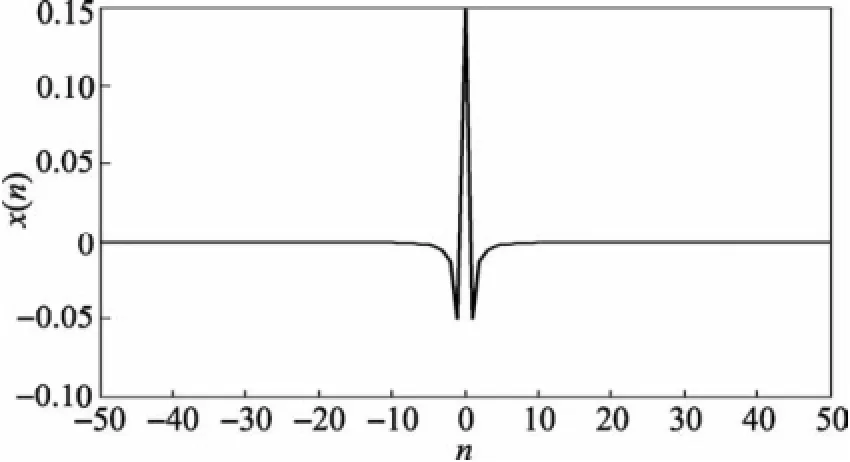
图7 指数窗斜变滤波器的单位脉冲响应
图8为指数型斜变滤波器的频率响应,由图可以看出,在大约最高频率的66%处,幅度达到最高值;在该频率点前,频响呈斜变趋势,符合斜变滤波器的特点;在该频率点后,幅度迅速下降,到最高频率处,减为0。显然,这种滤波器可以较好地抑制Gibbs效应,抑制高频噪声。
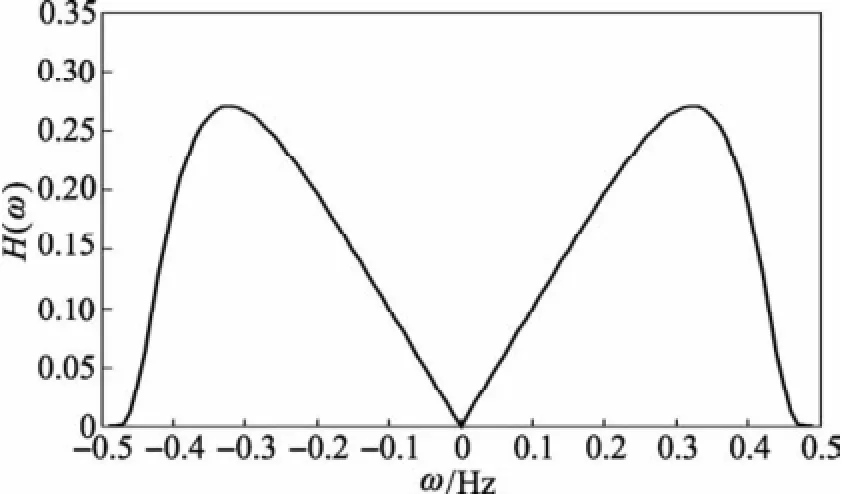
图8 指数窗斜变滤波器的频率响应
6 4种窗函数形成的斜变滤波器性能比较
6.1 频率响应比较
频率响应比较图见图9。sinc窗使斜变滤波器在最高频率处被“压低”到理想幅值的64%左右。这种“压低”,可以减少Gibbs效应并抑制高频噪声。Hamming窗使斜变滤波器在最高频率处被“压低”到理想幅值的8%。显然,这种滤波器相比SL滤波器,Gibbs效应更小,更能抑制高频噪声。但其缺点是频响过早就不再斜变,丧失了斜变滤波的特征。当投影信号本身的高频成分较多的时,重建误差会增大。
指数窗最接近矩形窗且过渡平稳。它使斜变滤波器在最高频率处幅值被“压低”到0。显然,该滤波器在这4种滤波器中,Gibbs效应最小,抑制高频噪声的能力最强。
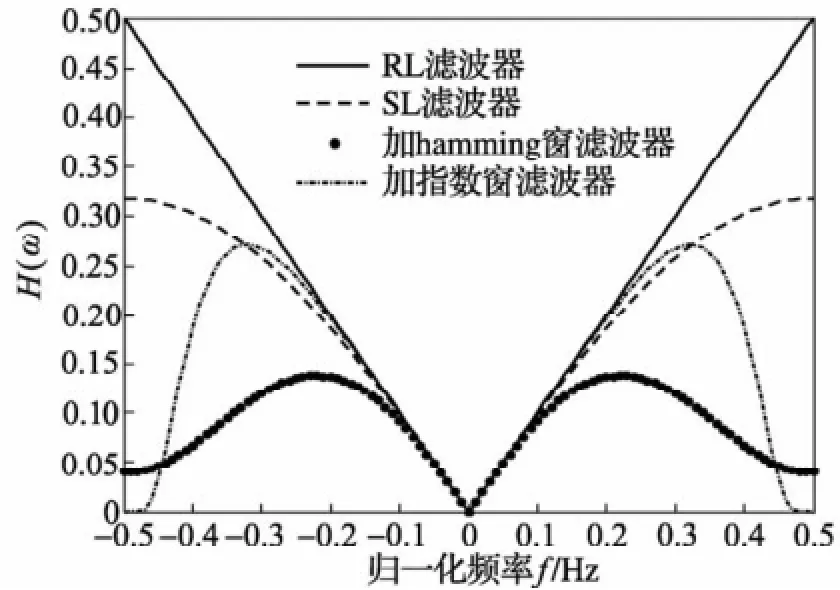
图9d=1时对应的4种实用斜变滤波器的频率响应
6.2 单位冲激响应的旁瓣衰减速度比较
对投影信号滤波时,斜变滤波器的单位脉冲响应取有限长度,一般取投影信号长度的2倍减1。然而在信号长度范围之外的区间,单位脉冲响应还有一定幅值的旁瓣在振荡。显然,如果旁瓣衰减速度快,则被截断后,丢失的信息少,精度就高。
图10为4种斜变滤波器在d=1时,在11~50范围内的旁瓣衰减情况。

图10 4种斜变滤波器的旁瓣衰减速度比较
由图10可以看出,RL滤波器的旁瓣衰减速度最慢,振荡明显,没有较好地消除Gibbs效应;SL滤波器和指数窗滤波器衰减最快,振荡较小,很好地消除了Gibbs效应。Hamming窗滤波器的旁瓣衰减速度居中。
6.3 数值实验
实验仿真模体采用Shepp-Logan模型,共采集180个角度的投影,角度间隔为1°,用线性插值方法反投影,重建图像为128×128的图像。比较采用4种不同的滤波器时,对应的CT图像的精度。精度用归一化均方距离判据d和归一化平均绝对距离判据r这2个参数来评估。重建结果的精度比较见表1。

表1 4种斜变滤波器重建出来的CT图像的精度比较
实验模型图像和重建出来的图像见图11。
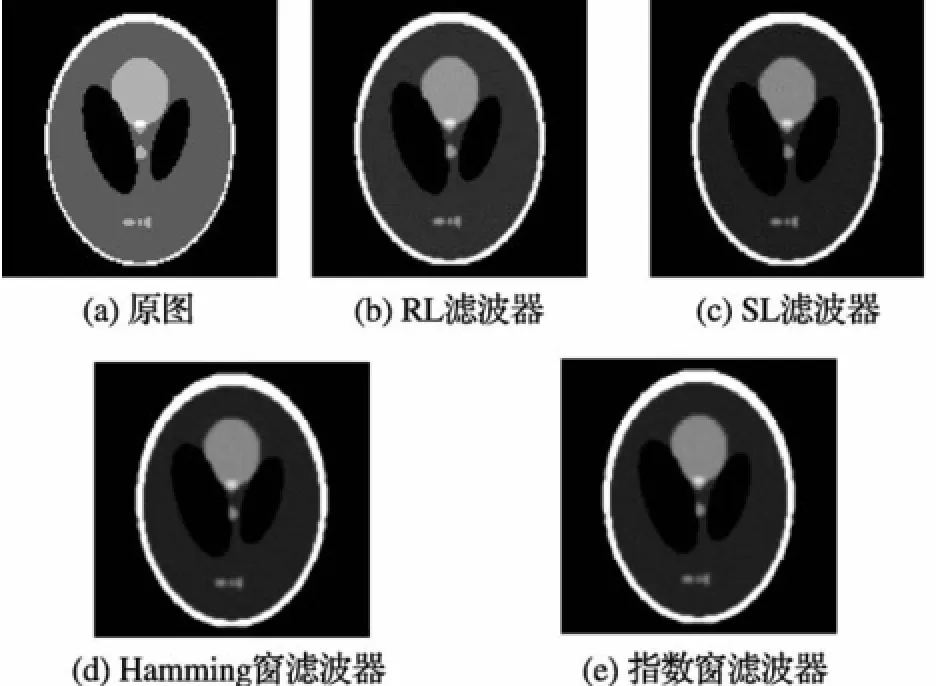
图11 不同的滤波器对应的不同的CT图像
由表1和图11可以看出,RL滤波器因为加矩形窗的缘故,Gibbs现象严重,误差较大;SL滤波器因为sinc窗的缘故,两种误差均比RL的小,减小了Gibbs效应;Hamming窗加了升余弦窗,使得归一化平均绝对距离判据r进一步减小;指数窗滤波器的重建图像的r最小,而此判据是描述大量小的误差,可见指数窗滤波器Gibbs效应最小,但该滤波器的d并不是最小的,而是处于中间位置,说明指数窗滤波器是一种折中性能较好的滤波器。
7 结 论
RL滤波器、SL滤波器、Hamming窗滤波器和指数窗滤波器是4种频域加窗滤波器。
通过理论分析窗函数性质、频率响应、旁瓣衰减速度以及仿真实验,表明RL滤波器是最简单实用的滤波器,但是振荡噪声明显;SL滤波器、Hamming窗滤波器和指数窗滤波器的振荡噪声均较小,其中指数窗滤波器的振荡噪声最小。
从兼顾归一化均方距离判据和归一化平均绝对距离判据的角度讲,SL滤波器是最优的滤波器。
[1] 秦然.基于神经网络的CT脑血管图像边缘检测算法[J].电子测量与仪器学报,2010,24(6):346-352.
[2] 马敏,王化祥,温丽梅.多相流CT系统的双对角化迭代算法[J].计量学报,2010,31(5):464-466.
[3] 乔志伟,魏学业,韩焱.基于算术傅里叶变换的滤波反投影算法的滤波过程的加速[J].计量学报,2010,31(5):385-389.
[4] Jiang Hsieh.Computed Tomography Principles,Design,Artifacts,and Recent Advances[M].Bellingham,WA:SPIE Optical Engineering Press,2004.
[5] 杨民,路宏年,傅健.基于卷积反投影CT重建的一种新型实用滤波函数[J].CT理论与应用研究,2000,9(S1):29-32.
[6] 张斌,潘晋孝.CT图像重建的新型混合滤波器[J].微计算机信息,2009,25(9):298-230.
[7] 刘晓,杨朝文.RL滤波函数的改进对卷积反投影图像重建的影响[J].四川大学学报(自然科学版),2004,41(1):112-117.
[8] 范惠荣,徐茂林,邱钧,等.关于CBP算法的一种新型滤波函数和它的性质[J].电子学报,2004,32(2):232-235.
[9] 徐茂林,邱钧,范惠荣,等.用一种新滤波函数作CT图像局部重建[J].计算物理,2004,21(3):362-368.
[10] Xu M L,Qiu J,Fan H R,etal.Local tomographywith a new filter[J].CT理论与应用研究,2004,13(1):54-58.
QIAO Zhi-wei
(School of Electronics and Computer Science and Technology,North University of China,Taiyuan,Shanxi030051,China)
The performance of the ramp filter has an important influence on image reconstruction.The designmethod of frequency domain window-adding is themainmethod.Four classicalwindow-adding filterswere designed,which are RL filter,SL filter,Hamming window filter and exponentwindow filter.The four filters characteristicswere analyzed using the unit impulse response and frequency response.The four filters were compared from the frequency response side and the sidelobe attenuation rate side.Theoretical analysis and simulation results show that the vibration noise of the exponent window filter isminimum and the SL filter is optimal as a whole.
Metrology;Ramp filter;Window function;Image reconstruction;Filtered back projection algorithm; Frequency response
TB973
A
1000-1158(2014)04-0382-05
10.3969/j.issn.1000-1158.2014.04.17
2012-03-28;
2013-12-03
国家自然科学基金(61071193,61171179)
乔志伟(1977-),男,山西洪洞人,中北大学副教授,博士,主要研究方向为图像重建、高性能计算以及数字信号处理等。zhiweiqiaook@nuc.edu.cn
doi:10.3969/j.issn.1000-1158.2014.04.18
Im pact of Frequency Domain W indow-adding for the Ramp Filter on Im age Reconstruction

