数字调制质量参数传递标准的研制

方 宏， 卞 昕， 周 鑫， 刘 科， 赵海宁

（中国计量科学研究院，北京 100013）

数字调制质量参数传递标准的研制

方 宏， 卞 昕， 周 鑫， 刘 科， 赵海宁

（中国计量科学研究院，北京 100013）

为了研制数字调制质量参数量值比对的传递标准，提出了一种基于星座图设计来实现对矢量信号发生器输出数字调制信号的调制误差进行准确设置的方法。给出了该方法的理论推导过程、实现方法，以及比对测量点的选取，最后通过测量实验，验证了所研制传递标准在比对测量点处的稳定性。

计量学；数字调制误差；星座图；误差矢量幅度；比对

1 引 言

数字调制信号是现代信息传输的主要载体，数字调制质量参数是衡量调制信号质量的重要参量，能否对该量值进行准确测量直接影响着现代无线（移动）通信相关产品的研发、生产的顺利开展，以及质量监督的有效性［1～5］。近年来，国内各计量单位纷纷建立了符合各种通信制式的计量标准装置，进行了大量的仪器校准业务，对于这些计量标准装置而言，数字调制质量参数是其中关键的参量之一，然而，由于目前尚缺乏完善的量值溯源体系将该量值溯源到基本量的国家基准上，因此导致各单位之间该量值的测量结果存在着一定程度的差异，量传水平参差不齐，因此迫切需要进行国内该量值比对，从而保障量值的统一。

对于大多数的比对项目而言，可以在市场上购置到性能和参数相对稳定的被测件或仪器作为传递标准，然而对于数字调制质量参数的比对，目前市场上尚未有一台矢量调制信号源（Vector Signal Generator，VSG）可直接作为传递标准使用，因为商用信号源技术指标中给出的数字调制参数指标只有在理想调制情况下的残余调制误差，并不能对所需的数字调制误差值进行设置［6，7］。而在实际通信系统中，由于信源和信道的非理想因素，使得实际测量的数字调制信号通常是带有一定调制误差的，如3GPP技术标准中对UMTS系统的误差矢量幅度（Error Vector Magnitude，EVM）值的规定是不超过17.5%［8］，因此，在对数字调制参数进行比对时，至少要对0～17.5%范围内的EVM测量值进行比对。为了完成数字调制质量参数计量标准（量值）的国内比对工作，本文提出了一种全新的方法用于研制可准确设置数字调制误差值的传递标准，并对其稳定性进行了验证。

2 理论模型

对于各种矢量调制方式，信号的幅度和相位均可以通过星座图上的星座点进行表示。然而，由于调制器硬件性能的缺陷或变化以及调制解调算法的精度等因素的影响，实际信号矢量与理想信号矢量是有误差的。因此矢量调制误差参数的定义是每个符号周期内，实际信号矢量点与其对应的参考星座点之间的误差，文献［1］将其称为数字调制质量参数，该误差主要包括幅度误差EM，相位误差EP和误差矢量幅度EV，见图1。

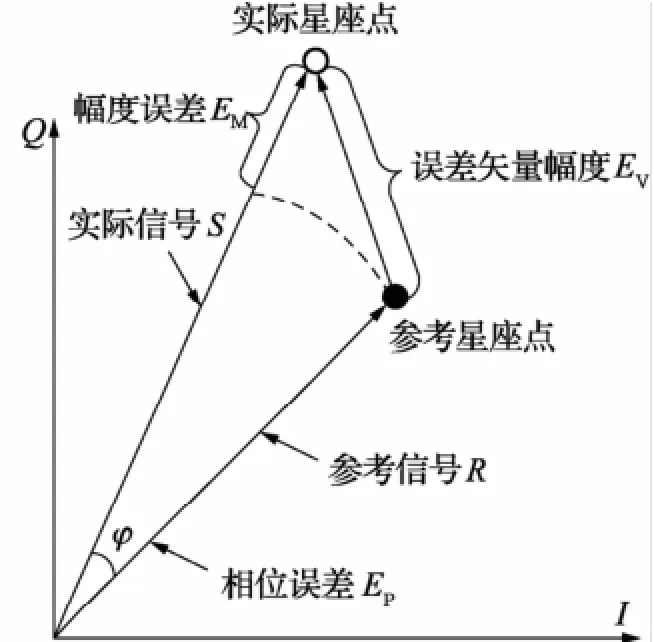
图1 矢量调制误差定义示意图

在实际测量中，它们是给出的一串码元的统计结果，通常用均方根值来表示［9，10］，幅度误差EM可以表示为

3 设计方法

目前，在使用VSG时，大多可以通过调节一些基带参数，如IQ增益不平衡、IQ相位不平衡或IQ偏置等，人为地恶化输出信号的调制质量，然而使用者并不能通过这些参数对输出信号的调制误差进行准确地设置。因此，本文的目标就是设计一种方法可以准确地在VSG上设置出带特定量矢量调制误差的数字调制信号，从而根据比对中需要的测量点，设计传递标准。本文提出通过预设基带星座图的方式来达到该目标，根据预设目标调制误差参量的不同分为以下3种方式。

3.1 预设目标为均方根幅度误差

当预设目标为均方根幅度误差EM时，为了隔离相位误差的影响，希望设计出的矢量调制信号仅带有幅度误差。图2中的实心点为参考星座点，将2个实际星座点设计在参考星座点与原点的连线上，且分布在参考星座点的两侧，见图2中的空心点。由于在解调过程中，参考星座点不是人为设定的，而是VSA根据实际星座点的功率平均值和所选的解调方式自动设定的，因此，这3个点必须满足功率归一化的关系

图2 预设目标为EM的第一象限星座图

此外，根据式（1）可知，2个实际星座点和参考星座点的相对位置决定了幅度误差EM

结合式（4）、式（5），在令c＝1的条件下，可以推导出

因此，对于预设的EM，可确定出2个实际星座点的相对位置。将第一象限的实际星座点对称地映射到第二、三、四象限中，坐标分别为（b，b）、（c，c）、（－b，b）、（－c，c）、（b，－b）、（c，－c）、（－b，－b）、（－c，－c），即可以得出满足预设目标EM的基带星座图。如果对于所选择的调制方式，每个象限中有多个参考星座点，如QAM调制方式，可以采用同样的方法，在每个参考星座点与原点的连线上设计2个实际星座点。

3.2 预设目标为均方根相位误差

当预设目标为相位误差EP时，为了隔离幅度误差的影响，希望设计出的矢量调制信号仅带有相位误差。图3所示的实心点为参考星座点，将2个实际星座点设计在以原点为圆心，以参考星座点到原点距离为半径的圆弧上，在参考星座点两侧，且∠AOB和∠AOC相等，见图3中的空心点。

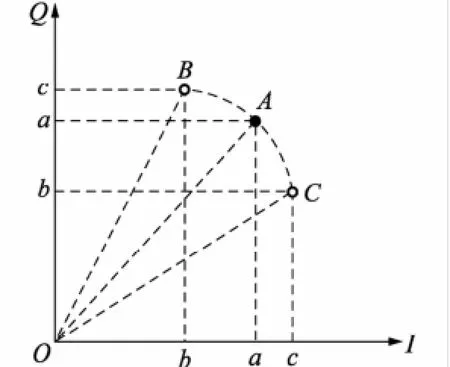
图3 预设目标为EP的第一象限星座图

根据功率归一化关系和EP的定义，可分别得出

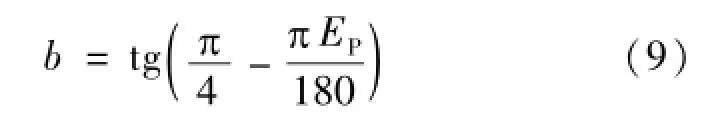
因此，对于预设的EP，可以确定出2个实际星座点的相对位置。将第一象限的实际星座点对称地映射到第二、三、四象限中，坐标分别为（b，c）、（c，b）、（－b，c）、（－c，b）、（b，－c）、（c，－b）、（－b，－c）、（－c，－b），即可以得出满足预设目标EP的基带星座图。如果对于所选择的调制方式，每个象限中有多个参考星座点，如QAM调制方式，可以采用同样的方法，在以原点为圆心，以每个参考星座点与原点距离为半径的圆弧上，设计2个实际星座点。

3.3 预设目标为均方根误差矢量幅度

当预设目标为误差矢量幅度EV时，为了能同

在令c＝1的条件下，可以推导出时反映幅度误差和相位误差的影响，希望设计出的矢量调制信号既带有幅度误差又带有相位误差，综合的效果正好是预设的EV值。同上文类似，图4所示实心点为参考星座点，在其周围设计4个实际星座点（空心点）。其中点C和点D为在参考星座点与原点的连线上，点B和点E为在以原点为圆心，以参考星座点到原点的距离为半径的圆弧上。

图4 预设目标为EV的第一象限的星座图

根据功率归一化关系和EV的定义，可分别得出

因此，对于预设的EV，可以确定出4个实际星座点的相对位置。将第一象限的实际星座点对称地映射到第二、三、四象限中，坐标分别为（b，b）、（c，c）、（b，c）、（c，b）、（－b，b）、（－c，c）、（－b，c）、（－c，b）、（b，－b）、（c，－c）、（b，－c）、（c，－b）、（－b，－b）、（－c，－c）、（－b，－c）、（－c，－b）。如果对于所选择的调制方式，第一象限中有多个参考星座点，如QAM调制方式，可以采用同样的方法，在每个参考星座点周围设计4个实际星座点。

目前常用的VSG都带有用户自定义IQ图的功能，即根据用户需要自定义矢量调制的星座图。通过手动设置的方式或者程序导入的方式将本文中设计的基带星座图配置到VSG中，由此，便可以实现根据用户预设的矢量调制误差进行矢量调制信号的输出。

4 传递标准的实现与稳定性验证

QPSK和16QAM调制是目前无线通信标准中最常使用的调制方式，因此设计比对测量点见表1。

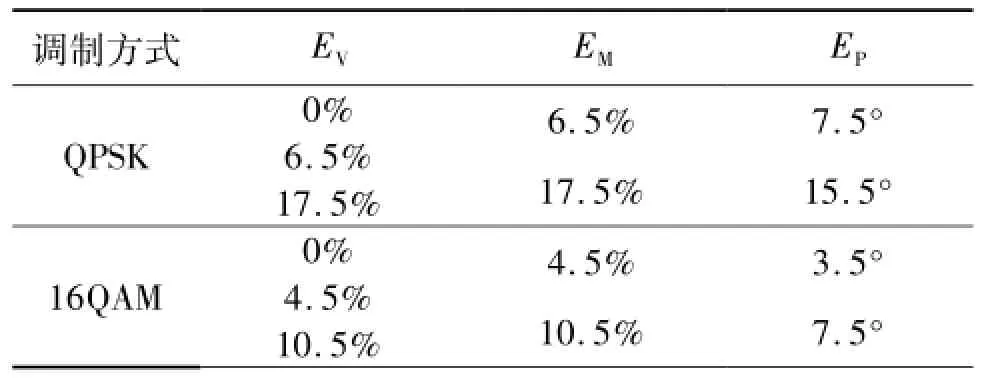
表1 比对测量点

选用Agilent公司的E4438C作为VSG，将设计的基带星座图配置到VSG中，分别为针对QPSK调制、16QAM调制，预设目标分别为EM、EP、EV这3种情况下导入VSG的基带星座图，见图5、图6。

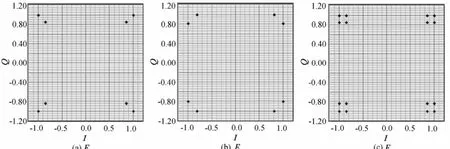
图5 QPSK调制方式中3种情况下设计的基带星座图

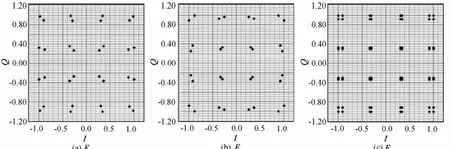
图6 16QAM调制方式中3种情况下设计的基带星座图

设置VSG的载波频率为1 GHz，信号电平为－10 dBm、滤波器为根升余弦型，α＝0.22，码率为2 Msps。生成数字调制信号，从VSG输出端输出。将生成的数字调制信号输入到VSA的输入端，本实验中选用RS公司带有VSA选件的FSUP作为VSA。设置VSA的载波频率为1 GHz、测量滤波器为根升余弦型，参考滤波器为升余弦型，α＝0.22，码率为2 Msps，参考电平设置为－5 dBm，解调方式为QPSK或16 QAM，星座图类型为NATURAL。

为验证传递标准设置参数的稳定性，对各测量点进行多次测量，统计测量结果的标准差，结果见表2，各标准差结果对应的测量点为表1中的对应位置。由表中结果可见，各测量点处的测量值标准差均较测量装置通常在对应参数上给出的不确定度小1～2个数量级，证明了本文研制的该方法的传递标准具有有足够的稳定性，可用于量值比对中。

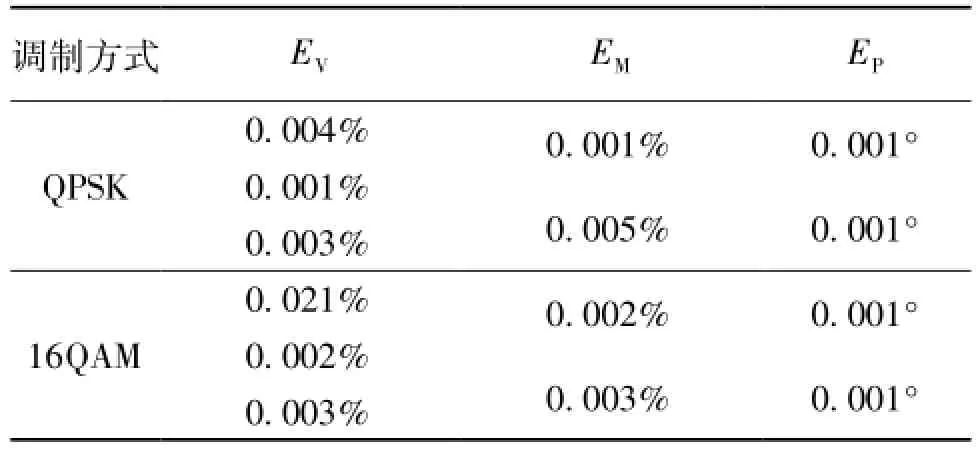
表2 传递标准测量值标准差（100次测量）

5 总 结

数字调制质量参数的量值溯源目前还存在较大缺口，全国性的量值比对将在一定程度上验证和提高该量值测量的一致性程度。针对市场上的VSG不能直接作为传递标准的问题，本文提出了一种基于预设基带星座图的方法，实现了使用商用VSG准确地设置各种矢量调制误差参数的目的，并实现了传递标准的研制，通过实际测量验证了传递标准在比对测量点处的稳定性，后续将使用该传递标准进行全国的数字调制质量参数量值比对工作。

［1］ 吴幼璋，赵海宁，于汇东，等.数字调制质量参数的校准和量值溯源［J］.计量学报，2005，26（3）：271－274.

［2］ 李伟，周峰，张睿，等.数字调制误差参量计量技术评述［J］.计量技术，2011，（1）：44－48.

［3］ 周鑫，赵海宁，何昭，等.WCDMA数字移动通信系统信道化原理及其在计量中的应用［J］.仪器仪表学报，2007，28（S4）：347－351.

［4］ Humphreys D A，Dickerson R T.Traceable Measurement of Error Vector Magnitude（EVM）in WCDMA Signals［C］／／International Waveform Diversity＆Design Conference，Pisa，Italy，2007.

［5］ Hudlicka M.Laboratory System for a Traceable Measurement of Error Vector Magnitude［C］／／Proceedings of the 39th European Microwave Conference，Rome，Italy，2009.

［6］ 周峰，张睿，郭隆庆，等.非理想传输通道对数字调制信号EVM的影响——理论、仿真和测量［J］.电子测量与仪器学报，2009，23（z1）：4－9.

［7］ Zhang R，Zhou F，Guo L Q，et al.Metrology of vector modulation error：problems and solution［C］／／27th conference on precision electromagnetic measurement，Daejeon，Korean，2010.

［8］ 3GPP TS 34.122 V8.3.0（2009－09）Release8［S］.

［9］ Mckinley M D，Remley K A，Myslinski M.EVM calculation for broadband modulated signals［C］／／ARFTG Microwave Measurements Conference，Orlando，USA，2004.

［10］ Fang H，Bian X，Zhou X，et al.The numerical simulation and experiment research for measurement of error vectormagnitude（EVM）［J］.Applied Mechanics and Materials，2011，103：199－204.

Development of Transfer Standard for DigitalModulation Quality Parameters

FANG Hong， BIAN Xin， ZHOU Xin， LIU Ke， ZHAO Hai-ning
（National Institute of Metrology，Beijing 100013，China）

In order to develop transfer standard of digitalmodulation quality parameters，a new method is proposed to set the modulation errors of the output digital modulation signal from vector signal generator accurately based on constellation diagram designing.Theoretical derivation，implementation and measurement points for comparison are presented.Stability of the developed transfer standard is verified by the statistics of the experimental data.

Metrology；Digitalmodulation errors；Constellation diagram；Error vectormagnitude；Comparison

TB973

A

1000-1158（2014）03-0263-05

10．3969／j．issn．1000-1158．2014．03．14

2012-04-20；

2014-01-11

中国计量科学研究院专项业务费项目（ABD11）

方宏（1982－），男，江西上饶人，中国计量科学研究院副研究员，主要研究领域为无线电计量。fanghong＠nim.ac.cn