基于分位数函数和Bootstrap分布的不确定度评定研究

宋明顺， 张俊亮， 方兴华

（中国计量学院，浙江杭州 310018）

基于分位数函数和Bootstrap分布的不确定度评定研究

宋明顺， 张俊亮， 方兴华

（中国计量学院，浙江杭州 310018）

最大信息熵方法是基于概率分布评定测量不确度的主要方法之一。其所依赖的高阶矩需要较大样本的测量数据，而校准／检测实验室的测量一般为小样本，故用最大熵方法评定小样本测量不确定度缺乏一定的可靠性。提出了基于分位数函数和概率权重矩作为约束条件的最大信息熵不确定度评定法，把矩的计算从高次降为一次，并结合遗传算法求解概率分布，用Bootstrap分布估计扩展不确定度和包含区间，解决了由分位数区间估计分布不对称所致的复杂计算问题。

计量学；不确定度评定；分位数；概率权重矩；最大熵原理；Bootstrap分布

1 引 言

最大信息熵方法（PME）是基于概率分布评定测量不确定度的常用方法［1］。利用PME确定概率密度函数（PDF）是在已知先验信息约束条件下通过使信息熵最大来得到的，即：

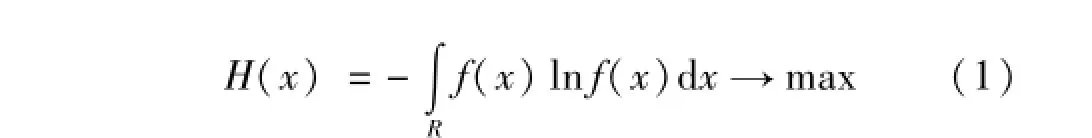
且式（1）有以下约束条件：

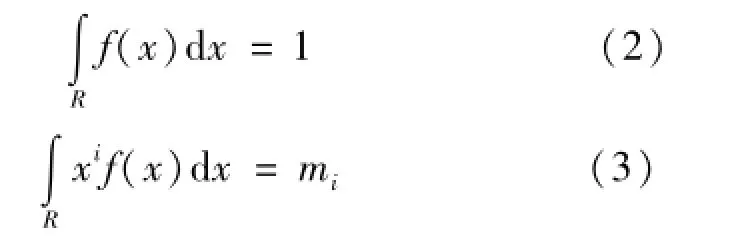
式中，H（x）为熵函数，f（x）为随机变量的概率密度函数，mi为第i阶原点矩，通常mi由测量样本给出，即：

通过求条件极值可得到测量值x的概率密度函数f（x），即：

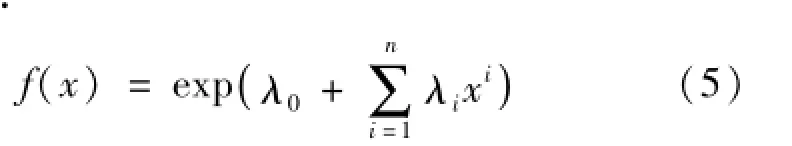
式中，λi为拉格朗日乘子。

λi的计算依赖于样本矩，样本矩的计算又依赖于给定的测量样本。理论上，样本矩阶次越高，所包含的信息量越大，求解的PDF越接近于真实分布。但高样本矩阶次带来两个问题：一是λi的计算问题，在实际的计算过程中，样本矩越高，求解方程的非线性化程度越严重，求解就越复杂，计算误差就比较大，如传统λi的计算方法L-M法［2］和拟牛顿法［3］，均不能很好地解决上述问题；二是样本量的问题，样本矩阶次越高，所需要的测量样本量越大，但在实际校准／检测工作中，样本量通常都是较少的，属于小样本测量（样本容量小于50），在小样本测量条件下，用PME求解PDF的可靠性大大下降。M.D.Pandey指出，在计算分位数的样本矩时，阶次取2～4偏差接近于0，效果比较好。

本文提出用概率权重矩（PWMs）为约束条件的分位数最大熵方法来求解小样本条件下的PDF，然后得到分位数的点估计，即可以由PDF求出最佳估计值及标准差，并用Bootstrap方法得到给定包含概率下的扩展不确定度及包含区间。

2 概率权重矩及分位数函数

针对小样本测量中PME评定测量不确定度存在的高阶矩问题，通过分位数函数及PWMs将矩的高阶次转化为低阶次，使其适用于小样本测量，降低了计算的复杂性，并且保证测量不确定度评定的可靠性。

2.1 概率权重矩（PWM s）

现在常用的PWMs的定义是由Greewood提出的［4］：

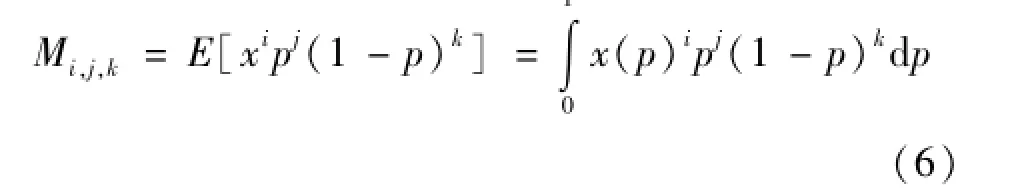
1

其中，以下两种PWM形式是简单而常用的。第1种：

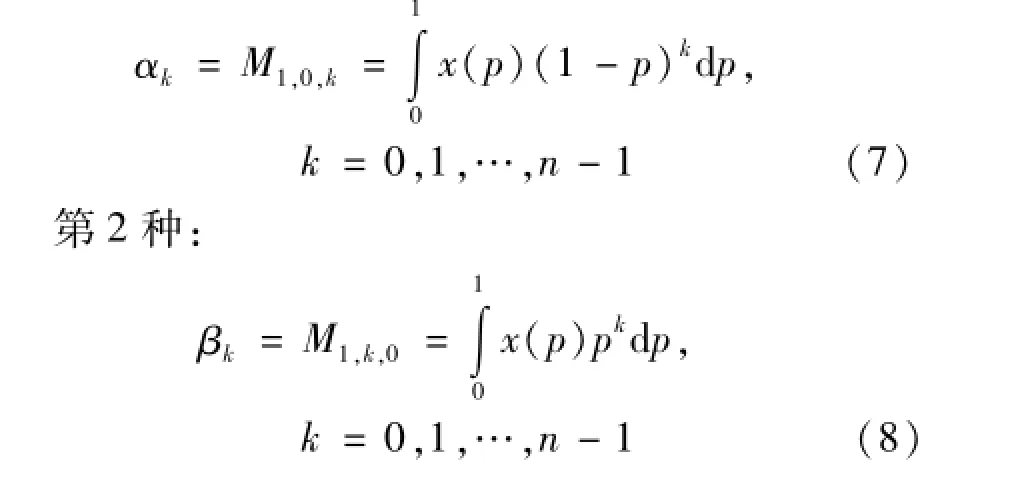
比较式（8）和式（7）可以知道，当样本容量为k时，αk，βk分别与最小、最大顺序统计量的期望有关，其关系式可表示为：

对于一个有n个顺序统计量的样本，ak，bk分别为αk和βk的无偏估计：

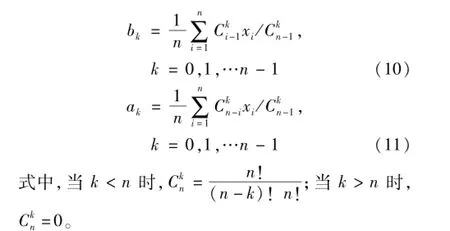
比较式（10）和式（4）可以看出，作为样本信息的提取方式，样本原点矩（mi）是求样本中每个数的幂的均值，即对样本数据进行非线性处理，它对样本的取值范围很敏感，特别是在小样本条件下，高阶矩不能够从小样本中准确地得到；PWMs是通过对样本信息作线性计算来提取样本信息的，它的优点在于对样本的边界值不敏感，高阶PWMs能从样本中比较准确地得出。因此，在小样本测量的条件下，高阶PWMs约束下得到的概率分布更为客观、合理。

2.2 分位数函数的矩

PWMs是数据顺序统计量的期望值，也可以解释为非负随机变量分位数函数的矩，分位数函数是分布函数的反函数。在非负随机变量的情况下，常用βk作为分位数函数的矩，这也是计算中常用的一种情况，由传统统计矩的定义知，k（k≥1）阶矩的定义为：

把式（3）与式（12）比较，x（p）类似于f（x），而概率p类似于随机变量x。分位数函数为一个连续函数，而且是非负，由于0≤x（p）≤∞，0≤p≤1。设：

根据式（12）和式（14），（βk／β0）可看作分位数函数x（p）的k阶矩。在实际的计算中，如果对测量数据样本作归一化处理，则β0＝α0＝1。对于这样的样本，βk便为分位数函数的阶矩。

3 测量不确定度的评定

现在来研究基于概率权重矩最大熵原理下的分位数函数测量不确定度的评定方法。

随机变量x的分位数函数x（p）的熵定义为：

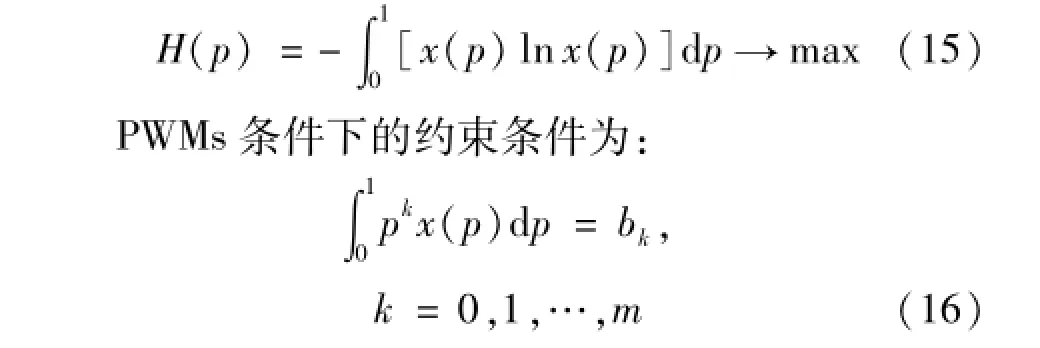
式中，bk为βk的无偏估计，m为考虑的概率权重矩的最高阶数。

考虑到其约束条件，分位数的最大熵函数可以写为：

对式（17）求导后得到PWMs为约束条件下用PME确定的分位数函数的表达式，即：

式中，拉格朗日乘子可以通过式（16）的约束条件来确定，即把式（18）代入式（16），得

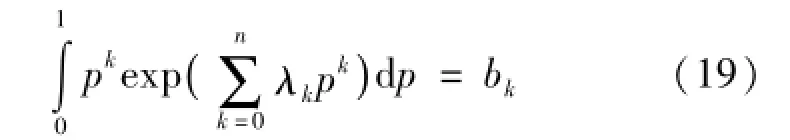
对式（19）变形，且令残差rk为：

残差rk表征着拉格朗日乘子估计的水平，残差越小，表明估计越准确。为求得拉格朗日乘子λk的值，需要对残差优化处理，故令

式中，ε无限接近于0，以此为优化过程的极值。

式（21）的求解，本文采用遗传算法予以解决［5］。通过分位数函数可以对测量结果进行不确定度评定。这种方法在小样本条件下不确定度评定比传统样本原点矩估计的评定效果更好。

分位数函数是分布函数的反函数。因此，通过对分位数函数求反函数，就可以得到随机变量的PDF，即：F（x）＝x－1（p），也可以直接通过分位数函数确定测量结果的最佳估计值和标准不确定度u：

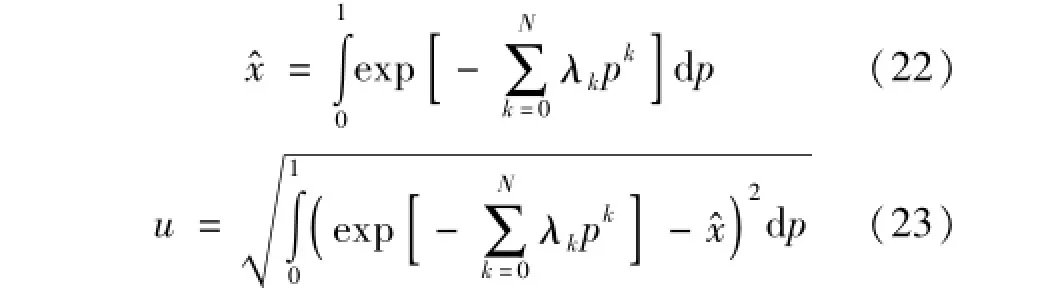
在给定包含概率p的条件下确定包含区间Up时，传统方法是先判断其分布是否对称，若对称，可根据式（24）来求解其指定概率下的包含区间：

Up＝［x（（1－p）／2），x（（1＋p）／2）］（24）

若分布函数不对称，通过文献［6，7］可发现，Bootstrap在区间估计方面应用很广，效果也佳，故本文采取Bootstrap估计来确定其包含区间。

4 Bootstrap区间估计

Bootstrap方法是一种再抽样统计方法。其基本思想是用已知的经验分布函数代替未知母体的分布函数，并通过再抽样技术获得统计量的Bootstrap分布，在此基础上就可进行统计推断，如求解统计量的标准差和包含区间等。

Bootstrap再抽样方法很多，本文采取的是非参数方法［8］。其主要思想是利用经验分布函数代替总体分布函数，从经验分布函数中抽取相同容量的样本来估计参数的抽样分布。从经验分布函数中抽样与对原始样本作有放回的抽样是等效的。

Bootstrap的区间估计基本过程是首先抽取一组Bootstrap样本，用遗传算法计算相应的统计量＝θ（，，…，Xn），如分位数x（p），称为Bootstrap估计量。重复再抽样B次，就可以获得B个Bootstrap估计量：

这B个Bootstrap估计量就提供了统计量的Bootstrap分布信息。有了统计量分布，就可以在此基础上进行推断统计量的包含区间。本文采用经验百分位数方法。Timmerman指出，经验百分位数方法的估计误差将以1的速度趋近于0。

将B个Bootstrap估计量)θ*i由小到大进行排序，由经验百分位数方法得到包含概率为1－α的包含区间估计为：

5 实例分析

已知大型工具显微镜3倍物镜长度重复测量样本，参见表1［9］。

表1 显微镜物镜长度测量数据mm

根据样本对测量结果进行不确定度评定。

由于样本容量为20，属于小样本情况，因此用PWMs为约束条件确定分位数函数，通过分位数函数来对样本进行不确定度评定，通过Bootstrap来对区间进行估计。此实例的计算，均采用Matlab程序完成。

（1）分位数函数的确定

在确定分位数的矩时，阶次越高，精度越高，但其复杂性也越大。故根据样本，利用式（10），计算得到分位数函数的前4阶PWMs，分别为：

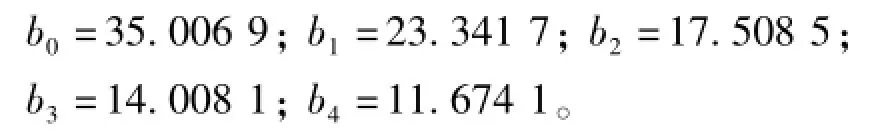
然后利用PME确定分位数函数表达式，如式（27）所示，对分位数函数求反函数即得到样本的分布函数。

（2）根据分位数函数进行不确定度评定

在得到分位数函数后，通过式（22）和式（23）来确定样本的最佳估计值x＾1和标准不确定度u1：

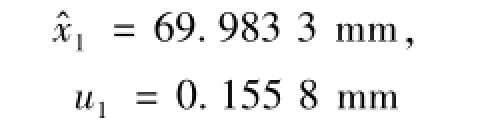
取Bootstrap再抽样次数B＝200，即对20个样本进行再抽样200次，得到200组样本量20的样本，分别对这200组样本进行基于概率权重矩的分位数函数计算，得到200个分位数函数xi（p），然后取对应p＝1－α的分位数值xi（α），将这200个新统计量xi（α）排序，依据式（25）得到包含概率1－α的包含区间，即在给定包含概率95%的条件下，得包含区间：

（3）评定结果比较分析

在GUM评定方法中［10］，最佳估计值和标准不确定度u2分别用样本均值和多次测量的标准差来表示。

在给定包含概率95%的条件下，GUM中的方法按正态分布对样本进行扩展不确定度评定，取包含因子k＝2，则此时的包含区间为］，最后计算得到包含概率95%下的包含区间为：［69.666 4，70.341 6］mm。

表2给出了GUM方法和用PWMs确定分位数函数进行不确定度评定的结果的对比。

表2 与GUM中不确定度评定结果比较mm

根据式（27）得到用GUM中正态分布假设的95%包含概率下包含区间两端点的概率为：p（69.666 4）＝0.136 5，p（70.341 6）＝0.959 7，也就是说，在此区间下包含概率p＝96%，超出了假设条件95%。因此在此例中，用正态分布假设来进行不确定度评定是不合理的。GUM方法是假设测量值服从正态分布的，只有在测量值真正服从正态分布时测量不确定度的结果才可靠；而PWMs确定分位数函数的方法没有任何概率分布的假设，无论测量值服从什么概率分布，都适用。

6 结 论

当测量数据样本为小样本（样本容量小于50）时，在PWMs约束条件下，用PME确定样本分位数函数，通过分位数函数来确定测量结果的最佳估计值和标准不确定度，用Bootstrap区间估计方法确定扩展不确定度及包含区间，不依赖数据的分布形式，有更广泛的应用范围，比GUM评定测量不确定度的方法要好。

［1］ Jaynes E T.Information theory and statisticalmechanics［J］.Phys Rev，1957，104（6）：620－630.

［2］ D′Antona G.Expanded Uncertainty and Coverage Factor Computation by High Order Moment Analysis［C］／／IMTC2004－Instrumentation and Measurement Technology Conference.Italy：Institute of Electrical and Electronics Engineers Inc，2004，234－238.

［3］ Pandey M D.Directestimation of quantile functions using the maximum entropy principle［J］.Structural Safety，2000，22（1）：61－79.

［4］ Greenwood J A，Landwehr J M，Matalas N C，et al. Probability weighted moments：definition and relation to parameters of several distributions expressible in inverse form［J］.Water Resourc Res，1979，15（5）：1049－1054.

［5］ Fang X H，Song M S.Estimation of Maximum－entropy Distribution Based on Genetic Algorithms in Evaluation of the Measurement Uncertainty［C］／／2010 Second WRI Global Congress on Intelligent Systems.Wuhan，China：Computer Society，2010，292－297.

［6］ 方兴华.在测量不确定度评定中用PME确定PDF的研究［D］.杭州：中国计量学院.2009.

［7］ Efron B.Bootstrap methods：another look at the jackknife［J］.The Annalsof Statistics，1979，7（1）：1－26.

［8］ Efron B.Nonparametric estimates of standard error and confidence intervals［J］.The Canadian Journal of Statistics，1981，9（2）：137－172.

［9］ Timmerman M E，TerBrak C J F.Bootstrap confidence intervals for principal response curves［J］.Computational Statistic＆Data Analysis，2008，52（4）：1837－1849.

［10］ 孙永厚，周洪彪，黄美发.基于最大熵的测量不确定度的贝叶斯评估方法［J］.统计与决策，2008，（12）：143－145.

［11］ BIPM，IEC，IFCC，ISO，IUPAC，IUPAP，OIML.Guide to the expression of uncertainty in measurement［S］. 2008.

Uncertainty Evaluation Based on Quantile Function and Bootstrap

SONG Ming-shun， ZHANG Jun-liang， FANG Xing-hua
（China Jiliang University，Hangzhou，Zhejiang 310018，China）

Maximum entropy is one of the chief methods in the evaluation of measurement uncertainty based on probability distribution，and the higher moments it depended on a larger sample of measurement data.However，measurement in calibration and testing laboratories is generally a small sample survey，so evaluation of measurement uncertainty based on the maximum entropy method for small samples lacks a certain degree of reliability.A method for uncertainty evaluation based on quantile function and probabilityweightingmoment is put forward as the constraint condition ofmaximum information entropymethod.By thisway，the high ordermoment is fell down for amoment，the probability distribution is solved with the combination of genetic algorithm，and the complicated calculation problem arising from quantile interval estimation of asymmetric distribution ismanaged aboutwith Bootstrap distribution estimation for expanded uncertainty and coverage interval.

Metrology；Uncertainty evaluation；Quantile functions；PWMs；Maximum entropy principle；Bootstrap distribution

TB9

A

1000-1158（2014）03-0300-05

10．3969／j．issn．1000-1158．2014．03．22

2013-02-21；

2013-07-23

国家自然科学基金（71071147）

宋明顺（1961－），男，山东蓬莱人，中国计量学院教授，主要从事计量基础、标准化和质量管理的研究。smsqm＠cjlu.edu.cn