地震时家具与墙相互作用关系的试验研究

包恩和 陈宜虎 邹 雪

（1.广西岩土力学与工程重点实验中心，桂林理工大学，桂林541004；2.桂林理工大学博文管理学院，桂林541006）

地震时家具与墙相互作用关系的试验研究

包恩和1陈宜虎2，*邹 雪1

（1.广西岩土力学与工程重点实验中心，桂林理工大学，桂林541004；2.桂林理工大学博文管理学院，桂林541006）

通过振动台试验，以松木制模型的尺寸、模型与墙体之间的间距以及试验加载的频率、加速度等为主要参数，着重研究：①家具与墙体之间的距离对两者相互作用的影响；②家具滑移、移动与墙体之间相互作用和试验加载的频率、加速度等之间的关系；③家具尺寸对家具滑移、移动等的影响。试验结果表明：模型与墙体发生碰撞后，其滑移量随试验加载频率减小而明显增加；试验加载频率高时，模型的移动量较小，将家具模型与墙体离开一定距离后可以防止两者之间发生碰撞；与碰撞体碰撞后的模型的滑移量最大值为单体滑移量最大值的2倍以上。

家具，滑移，墙壁，振动台实验

1 引 言

震害对于人类的生活有着巨大的影响，如建筑结构的震致破坏、倾覆等所造成的人员伤亡及财产损失等。有关地震时结构的损伤、倒塌与震害关系的研究一直以来是学界和工程界的研究“热点”。

然而地震时房屋非结构构件（墙板、幕墙）以及房屋中的家具设备、器物等非结构物在地震中的反应的研究较少。关于非结构构件（墙板、幕墙），文献［1，2］通过大型振动台试验，研究隔震钢结构在长周期地震作用下墙板的损伤情况。研究指出，除隔震层，其他层最大层间位移角R＝0.05时，墙板有损伤，但是没有破坏。地震中，但如家具、电器摇晃、移位或倾倒，吊灯等悬挂物摇晃或坠落，家中的摆设、超市货架上瓶罐摇晃或倾倒等，诸如此类的情况所造成的危害也是相当大的［3，5］。根据文献［6，7］，本文以式（1）为前提，通过振动台试验，着重考察：①家具与墙体之间的距离对两者相互作用的影响；②家具滑移、移动与墙体之间相互作用和地震波的频率、加速度等之间的关系；③家具尺寸对家具滑移、移动的影响等，从而对地震作用下，家具移动、滑移与其周边墙体之间相互作用的关系进行研究，为今后相关工程应用提供基础研究依据。

式中，μ为家具与楼地面之间的摩擦系数；b，h分别为家具的宽度和高度。

2 试验概况

2.1 实验模型与实验设备

实验模型见图1，尺寸参数详见表1，实验示意图详见图2—图5，为防止实验模型在振动作用下发生侧向旋转而影响实验结果的准确性，试验中专门在试验模型两侧设置了L形角钢导轨加以限制，详见图5。墙体与实验模型之间的间距C设置为C＝10 mm，C＝20 mm及无墙体设置三种情况。实验模型A、B的底面积相同，宽度B与高度H之间的比值分别为1.00和0.67两种情况。实验模型采用松木制作，为了降低松木表面粗糙对实验模型与振动台之间摩擦系数的不利影响，在实验模型底面四角分别设置了图钉，振动台的平台为不锈钢钢板，图钉与振动台之间摩擦系数为μ，摩擦系数的求法如下：在试块上慢慢加力（F），摩擦系数和滑移量之间的关系见图6。摩擦系数公式为

其中，mg表示自重。

从图中得到的摩擦系数的范围为0.18～0.28。试验中模拟墙体的碰撞体采用与实验模型相同的材料制作而成。

表1 模型参数Table 1 M odel parameters

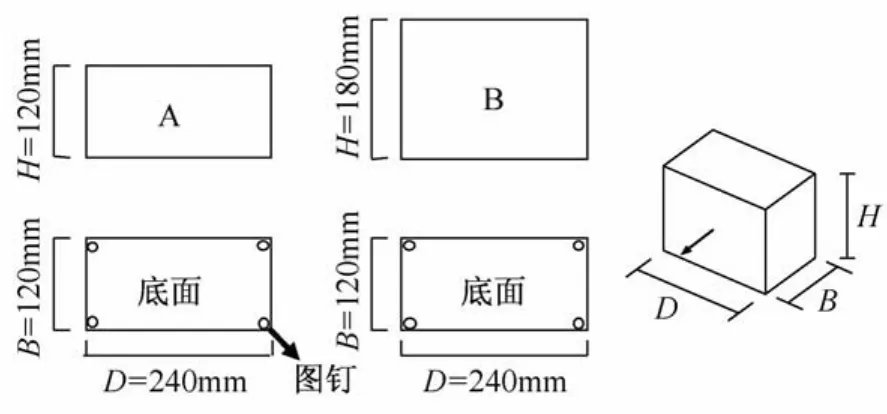
图1 试验模型尺寸Fig.1 Model size

图2 实验示意图Fig.2 Testmodel

图3 试验体加固示意立面图Fig.3 Elevation of strengtheningmeasurement

图4 试验体加固示意平面图Fig.4 Plan of strengtheningmeasurement

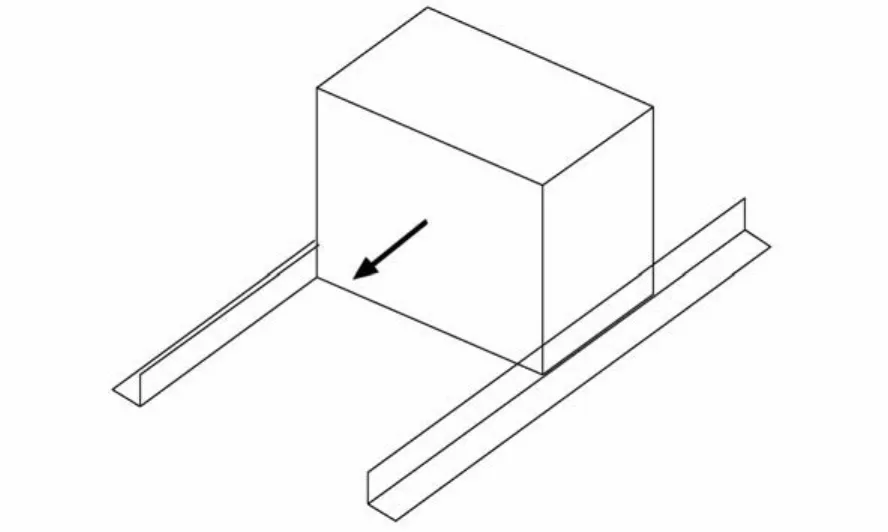
图5 试验体旋转控制图Fig.5 Diagram of rotation control figure ofmodel

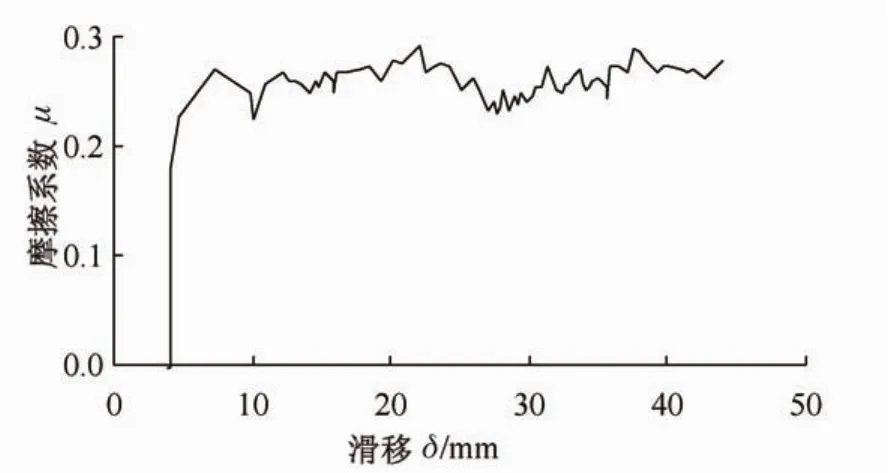
图6 摩擦系数和滑移量之间的关系Fig.6 Relation between friction cofficient and slip

2.2 试验荷载设计

本试验中，设计荷载采用以EL CENTRO NS、HACHINOHE1968 NS为基准的最大加速度a0调整为振动台地震波极限值550 cm／s2后的地震波见图7，还有图8所示的正弦波，该正弦波在T秒内即可达到峰值。试验加载时间均为10 s。正弦波的频率f及最大加速度a0如表2所示。根据文献［8］，振动台的振动加速度a0（t）如式（3）、式（4）所示。实验模型的位移采用位移计进行测量。设定实验模型朝向碰撞体移动的位移为正，背向碰撞体移动的位移为负。

式中，T正弦波达到峰值的时间段。

图7 输入地震波Fig.7 Seismic wave input

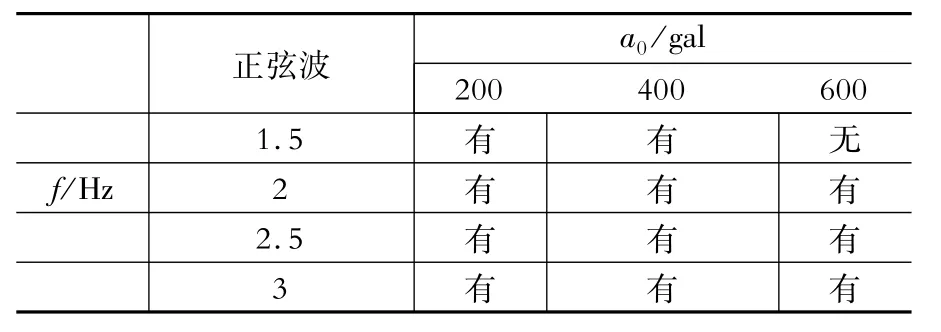
表2 正弦波的频率f及最大加速度a0Table 2 Sine wave frequency f and maximum acceleration a0

图8 正弦波时程Fig.8 Time history of sine wave

3 试验结果

3.1 模拟地震波作用下的试验结果

实验模型A在地震波EL CENTRO NS、HACHINOHE1968 NS作用下的试验位移、振动台加速度a与试验加载时间之间的关系如图9、图10所示。

图9 地震波EL CENTRO NS的试验结果Fig.9 EL CENTRO NS seismic wave

图9 （a）为试验输入地震波时程，最大加速度550 cm／s2，加载时间10 s。图中①和②是对应图9（c）C＝10 mm时模型与墙体碰撞的瞬间点；图9（c）中模型与墙体两次发生了碰撞：①点处瞬间模型与墙体只接触，同单体实验图9（b）相比，滑移量变化不大，这是因为模型与墙体碰撞的加速度迅速减小，墙壁产生的反作用力也迅速减小的原因。②点处瞬间模型与墙体发生了碰撞，碰撞后地震的加速度迅速增加，墙体产生的反作用力迅速增加，模型飞出，因此模型的移动轨道同单体实验图9（b）相比出现了反向滑移。图中③是对应图9（d）C＝20 mm时模型与墙体碰撞的瞬间点，碰撞后在墙体的反作用力作用下模型飞出，此后模型的移动规律相同于图9（c）中②点瞬间后模型移动情况。图9（c）、（d）中，模型的最大滑移量分别为δ1＝70 mm和δ2＝50 mm。即在试验中，模型均出现较大的滑移。图中时间段A和B，因输入地震波加速度较小，模型A未产生滑移。图9（c）、（d）中，碰撞后的时间段C内模型滑移的规律相似图9（b）单体运动。图10（a）为试验输入地震波HACHINOHE1968 NS时程，最大加速度550 cm／s2，加载时间10秒。图中①和②是对应图10（c）和图10（d）中，模型与墙体碰撞的瞬间点。从图10可知，模型与墙壁发生碰撞前，模型滑移时程单体实验图10（b）比较滑移量仍毫无变化；在①、②与墙壁发生碰撞的瞬间之后，地震加速度迅速增加，墙壁产生的反作用力迅速增加，模型在墙壁反作用力下飞出，模型的移动轨道与单体实验图10（b）相比出现反向滑移。图10（c）、（d）中，模型最大滑移量分别为δ1＝55 mm和δ2＝95 mm。图中时间段A和B均表示模型A未产生滑移。图10（c）、（d）中，碰撞后的时间段C内模型滑移的规律相似图10（b）单体运动。

另外碰撞时的加速度，图9（a）与图10（a）中（标注×），图9（a）EL CENTRO NS是负加速度时发生相撞，地震波HACHINOHE1968 NS中（图10（a）），正加速度时模型与墙体碰撞。然而移动量δ1和δ2与碰撞加速度的正负无关，与碰撞后短时间内的地震波加速度的增减情况有关。碰撞瞬间后加速度增加幅度越大，墙体的反作用力增加幅度越大，移动量增加越明显；反之，移动量变化越不明显。

3.2 正弦波作用下的试验结果

正弦波（f＝2.0 Hz，a0＝400 gal）时试验模型A的单体实验以及C＝10 mm、20 mm时的位移与时间之间关系图如图11所示。图11（a）中①和②是对应图11（c）C＝10 mm时模型与墙体碰撞的瞬间点；图11（c）中模型与墙壁两次发生了碰撞，①瞬间后模型滑动与单体实验图11（b）比较滑移量变化不大；②瞬间模型与墙体发生了再次碰撞，在那瞬间墙壁发生反作用力，模型飞出，模型的移动轨道与单体实验图11（b）相比出现反向滑移。图11（a）中③、④对应图11（d）C＝20 mm时模型与墙体碰撞的瞬间点，碰撞后模型移动规律同图11（c）情况。图11（b）、（c）和（d）中，模型最大滑移量分别为δ0＝20mm、δ1＝60mm和δ2＝65 mm。反映出模型在试验中，均出现较大的滑移。若碰撞后短时间内加速度均为增大，则碰撞瞬间的加速度值越大，滑移量也就越大。

另外，正弦波试验的模型A、B的移动量δ0、δ1、δ2与最大振动加速度和振动频率之间的关系图如图12所示。

图10 地震波HACHINOHE1968 NS的试验结果Fig.10 Tect resalts under HACHINOHE1968 NS seismic wave

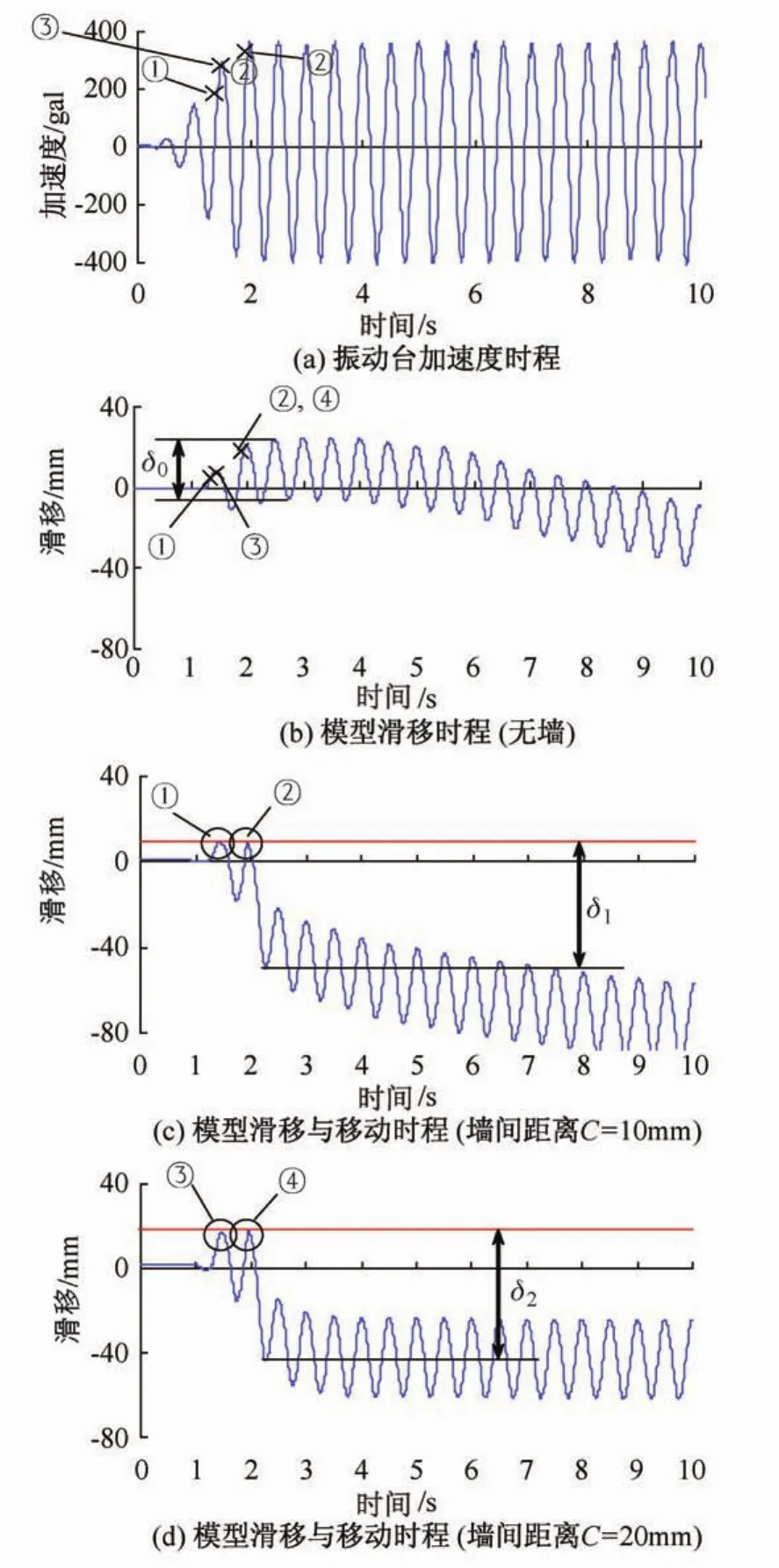
图11 正弦波试验结果Fig.11 Tet resalts under sine wave

根据上图12（a）、（b）可知，模型A、B的结果基本一致，从而可得：家具的滑移与家具的宽高比关系不明显。加速度越大，移动量越大；频率越小，移动量越大。最大加速度不大于200 cm／s2时，试验模型不产生滑移。当最大加速度超过200 cm／s2后，移动量随加速度的增加而增加。基本上碰撞后实验模型的移动量都增加。长周期时，单体的移动量大，所以与墙体碰撞的可能性高。短周期时，单体的移动量小，将家具与墙体离开一定距离后可以防止两者之间发生碰撞。由以上试验可知：1＜δ2／δ0＜2和1＜δ1／δ0＜2等关系。

根据正弦波作用下摩擦系数μ为0.18～0.28以及宽高比为0.67以及1的条件下，模型A、B的加速度与滑移量的关系结果（图12），整合并绘制滑移量与加速度之间的关系，如图13所示。可以发现基本呈指数函数的增长趋势，当加速度较小为200 cm／s2时，模型的拟合程度较好，当加速度为400 cm／s2或者600 cm／s2时模型的拟合程度误差较大，拟合得到如下公式：

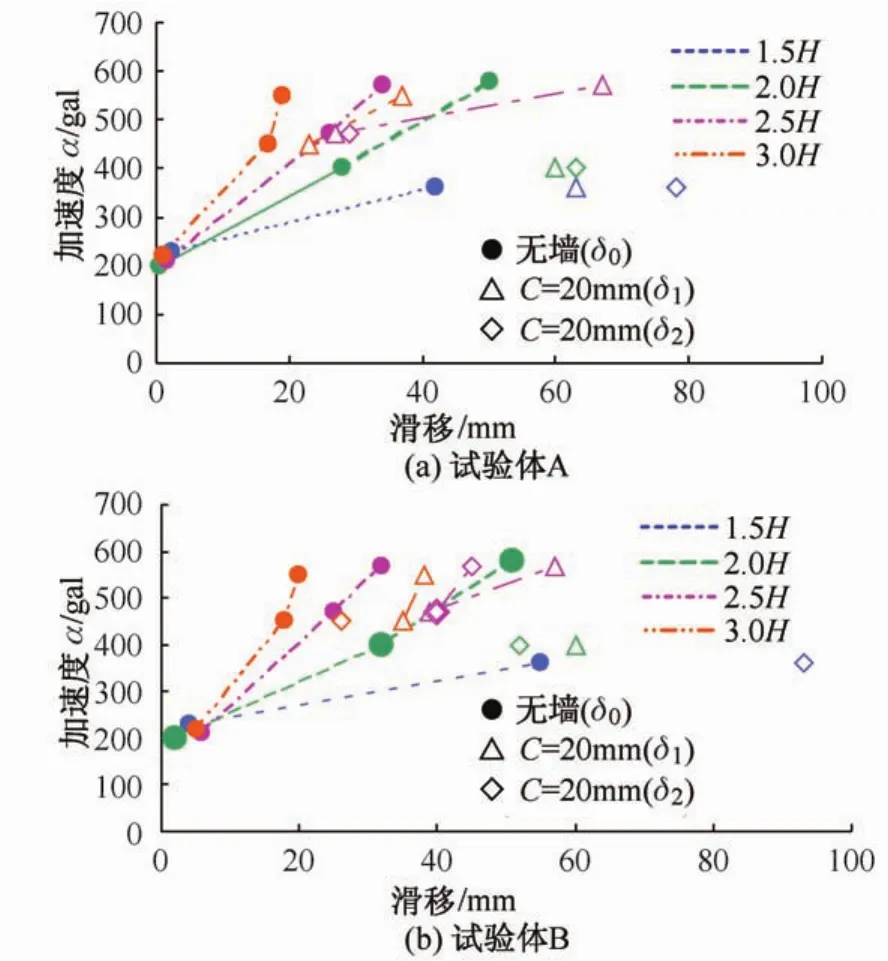
图12 正弦波试验模型的加速度与滑移量关系Fig.12 Relationship betweer acceleration and slip under sine wave

图13 移动量与加速度模型Fig.13 Slip and acceleration model

4 结 论

本文通过振动台试验，以松木制模型的尺寸、模型与墙体之间的间距以及试验加载的频率、加速度等为主要参数，在μ为0.18～0.28范围内，以及满足公式（1）的前提下，研究了地震时家具滑移与其周边墙体的相互作用关系，本次试验结果如下：

（1）地震实验时，试验模型与墙体之间发生碰撞后，短时间内加速度增加幅度越大，墙体的反作用力增加幅度越大，滑移量增加越明显；反之，滑移量变化不明显。

（2）正弦波实验时，若碰撞后短时间内加速度均为增大，则碰撞瞬间的加速度值越大，滑移量也就越大。当试验加载的频率越小时，实验模型滑移量的增加越明显。

（3）模型与墙体碰撞后，试验模型的滑移量最大值为单体滑移量最大值的2倍以上。

（4）正弦波作用下，家具的滑移量与加速度关系拟合后基本上呈指数函数曲线关系。

［1］ 栄弘朗，山田晃平，鳥谷修平等.外装カーテンウォールの大変形時における挙動［J］.日本建筑学会大会学術講演梗概集，B－2，2007，8：561-562.

［2］ 山田晃平，栄弘朗，谷修平等.震動台実験におけるカーテンウォールの挙動について［J］.日本建筑学会大会学術講演梗概集，B－2，2007，8：563-564.

［3］ 特定非営利活動法人（NPO）耐震総合安全機構、耐震総合安全性指針作成委員会.耐震総合安全性指針（案）［M］.2005.

［4］ 刘兴诗.汉川大地震的回顾与反思［J］.成都理工大学学报（社会科学版），2008，6：1-6.Liu XinShi.Review and reflection on Wenchuan earthquake in Sichuan［J］.Journal of Chengdu University of technology（Social Sciences Edition），2008，6：1-6.（in Chinese）

［5］ 罗珊，关惠元.柜类家具防震减灾设计探讨［J］.山西建筑，2012，38（36）：26-27.Luo Shan，Guan Huiyuan.A discussion on the cabinet furniture design for earthquake［J］.Shan Xi Architecture，2012，38（36）：26-27（in Chinese）

［6］ Kaneko M，Hayashi Y.Overturning criteria and horizontal displacements of rigid bodies to earthquake excitations［J］.Journal of Structural Engineering（Transactions of AIJ），1997，43（3）：451-458.（In Japanese）

［7］ Kaneko M，Hayashi H.Evaluation of sliding displacement of furniture during earthquake［J］.Journal of architecture and building science（Transactions of AIJ），1999，8（6）：73-78.（in Japanese）

［8］ Kaneko M，Hayash Y.Fundamental study on overturning limit of rigid bodies［J］.Journal of Structural and Construction Engineering（Transactions of AIJ），1996，479（1）：41-49.（in Japanese）

Study on the Interaction between Furniture and its Surrounding W alls in Earthquake

BAO Enhe1CHEN Yihu2，*ZOU Xue1
（1.Guangxi Key Laboratong of Geomechanics and Geotechnical Engineering，Guilin University of Technology，Guilin 541004，China；2.Bowen College of Management，Guilin University of Technology，Guilin 541006，China）

By shaking table testmethods，considering the key parameters such as pine-model dimensions，the distances between themodel and its surrounding walls，the frequency and acceleration under the loading，this papermainly focused on：（1）the interaction based on the distance between the furniture and the walls；（2）the relationship between the furniture slide／movementwith the interaction of its surrounding walls and，the frequency and acceleration under the loading；（3）the effecton the furnituremovementand slide considering the size of the furniture.The test results showed that：after the collision with the walls，the slippages of furniture increasewith the decrease of the loading frequency；and themovements are smallerwith the higher loading frequency；keeping a certain distance from the wall could prevent the collision；themaximal slippage is two times as big as thatwithout a collision.

furniture，slippage，wall，shaking table test

2013－11－16

广西自然科学回国基金项目（2011GXNSFC018004）；广西自然科学基金重点项目（2010GXNSFD013011）；广西高等学校特色专业及课程一体化建设项目立项（GXTSZY232）；广西矿治与环境科学实验中心项目（KH2012YB027）。

*联系作者，Email：cherif2009＠gmail.com