超高层建筑施工全过程竖向变形效应研究

马跃强

（1.上海建工二建集团有限公司，上海，200080；2.上海建筑工程逆作法工程技术研究中心，上海，200080）

超高层建筑施工全过程竖向变形效应研究

马跃强1，2，*

（1.上海建工二建集团有限公司，上海，200080；2.上海建筑工程逆作法工程技术研究中心，上海，200080）

依据欧洲规范EC2关于混凝土弹性模型、收缩、徐变随时间变化规定，考虑施工顺序加载、竖向构件压应力差异、伸臂桁架后连接、下料长度调整等因素，结合某超高层建筑结构，实现了施工全过程模拟，获得各施工阶段外框架柱和核心筒剪力墙的竖向变形量及差异，对施工过程中关键构件的承载力进行验算，同时比较了后连接方案对水平伸臂桁架内力的影响。分析结果表明：在超高层设计时必须考虑混凝土收缩徐变等非荷载作用下的变形，竖向构件应考虑竖向变形而产生的压缩量进行预调整，采用后连接的施工措施可以减小水平伸臂桁架的内力。

超高层结构，施工全过程，竖向变形，下料长度调整，后连接施工

1 引 言

超高层建筑的设计除了需要在结构体系、抗震抗风设计等方面有更高的要求之外，还需要考虑非荷载作用下的结构变形和内力分析。在长期荷载作用下，由于混凝土徐变和收缩性能，导致结构构件发生竖向变形，影响层净高、楼板平整度或非结构构件的正常使用，竖向构件之间的差异变形引起水平杆件次内力，对结构安全造成不利影响［1-5］。

超高层结构竖向变形及差异效应问题需要在概念设计、计算分析、施工措施等方面加以分析和控制。《高层建筑混凝土结构技术规程》（GJ 3—2010）［6］中规定：对于混合结构，计算竖向荷载作用时，宜考虑柱、墙在施工过程中轴向变形的影响，并宜考虑在长期荷载作用下由于钢筋混凝土筒体的徐变收缩对钢梁及柱产生内力的不利影响，但是规范对如何考虑竖向变形差异效应没有明确的规定。

结合某超高层建筑项目，本文介绍了施工过程分析模拟的计算方法，对各施工阶段不同构件的竖向差异变形进行研究，对施工过程中构件进行验算，并考虑了施工次序对水平伸臂桁架内力的影响。

2 工程概况

某超高层建筑项目为甲级写字楼，地上65层，地下3层，建筑屋顶高度为343 m，主屋顶结构高度为298.6 m。结构采用三重结构体系抵御水平荷载，由钢筋混凝土核心筒、外框架及构成核心筒和钢管混凝土柱之间相互作用的伸臂桁架及腰桁架组成。加强层布置在设备层内，分别在第22和38层。

结构竖向构件混凝土强度为C40－C60，核心筒墙厚从底部1 200 mm逐渐收至400 mm，底部加强区、加强层与框架梁相连处埋设型钢。平面主要采用16根φ1600－φ1000钢管混凝土柱（壁厚32～24 mm，混凝土强度等级为C40－C60），角部采用6根φ1200－φ600钢管混凝土小截面柱子构成。典型框架梁截面为H780×400×20× 25，主梁为H550×300×12×22。

图1 典型楼层平面图（单位：mm）Fig.1 Typical floor plan（Unit：mm）

3 施工全过程分析方法

3.1 计算方法

传统工程设计分析对象为恒定结构物，结构体系已给定，结构竖向荷载亦不变。分析时将全部竖向荷载一次性全部施加在结构上。但事实上，高层建筑结构是自下而上逐层施工，竖向变形也在不断积加，因此可以将施工分成一系列施工阶段，对各阶段进行有限元求解，得到各阶段的结构变形状况［7］。

采用有限元软件MIDASGEN，施工过程分析计算步骤如下：

（1）基于设计资料一次性建立整体结构模型。

（2）依据实际工期，将整体结构定义为若干施工阶段，每一阶段的计算以上一阶段的平衡状态为计算初始状态。

（3）依据实际施工进度，依次激活相应阶段单元，定义相关材料参数、荷载及边界条件，从而得到施工阶段模型并进行求解，实现施工全过程跟踪模拟。

3.2 混凝土分析模型［8-10］

1）混凝土弹性模量随时间的变化

依据欧洲规范Eurocode2弹性模型随时间的变化可以用下式描述：

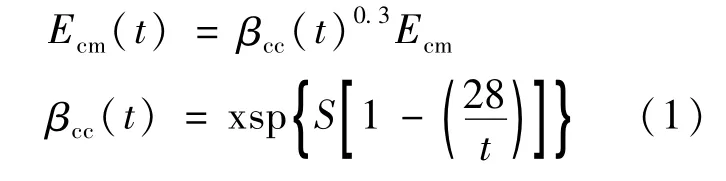
式中，Ecm是浇筑后第28天时混凝土的弹性模量值；Ecm（t）是浇筑后第t天时混凝土的弹性模量值，t是以天为单位的混凝土龄期；S是取决于水泥类型的系数，对于快硬高强水泥，S＝0.20。

2）混凝土的徐变

混凝土的徐变和初始应变的比值称为徐变系数，徐变系数可以用下式计算：

式中，φ0为名义徐变系数；βc（t，t0）是描述加载后徐变随时间发展的系数。可以用下式计算：

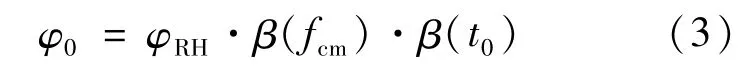
式中，φRH是考虑环境湿度对名义徐变系数影响的因子；β（fcm）是考虑混凝土强度对名义徐变系数影响的因子；β（t0）是考虑混凝土加载龄期对

式中，n＝Es／E0为弹性模量比值；μ＝As／bh为配筋率；λ为混凝土相应应力的受拉变形塑性系数，对轴心受拉，λ＝1.0。

3.3 施工工况

为了模拟弹性模量、徐变、收缩随时间的发展，将整个结构分为若干个不同的组，假定整个结构以组为单位向上施工，本项目施工阶段划分如图2所示。同一个组在不同的施工阶段有不同的弹性模量、徐变和收缩值，同时实现按照施工顺序加载计算结构的竖向变形与差异以及由此引起的内力。

在计算混凝土随时间变化的弹性模量、徐变、收缩时，需要明确施工中材料、环境条件、施工进度、施工顺序等情况。依据本工程实际情况和工程经验对此做出如下假定：

（1）核心筒剪力墙和钢管混凝土柱中使用的水泥为快硬高强水泥；名义徐变系数影响的因子。

3）混凝土的收缩

混凝土的收缩应变由两部分组成，即干缩应变和自生应变。

式中，єcs是总收缩应变；єcd是干缩应变；єca是自生应变。

干缩应变随时间的发展可以用下式计算：

式中，εcd，0为基本干缩应变；kh是依赖于构件名义尺寸h0的系数；βds（t，ts）是与时间和构件名义尺寸h0有关的系数。

自生应变用下式计算：

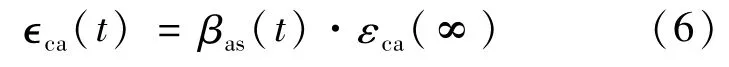
式中，εca（∞）＝2.5（fck－10）·10－6；βas（t）＝1－exp（－0.25t0.5）。

4）含钢率对收缩应变的影响

对称配筋构件，若混凝土的自由收缩应变єch为基本未知量，混凝土的拉应变为єc＝єcs－єs。两者的应力分别为σs＝єsEs，σc＝λ（εshєs）E0截面的平衡方程为

解之得：

图2 施工阶段Fig.2 Construction stages

（2）施工环境相对湿度取为80%，温度为25℃；

（3）钢管混凝土柱和核心筒剪力墙的加载龄期均为3天；

（4）施工速度为每层5天，外框架柱的施工滞后于核心筒7层，在加强层处，施工速度为每层8天。

4 竖向变形差异效应研究

4.1 竖向变形量及差异

选取外框架钢筋混凝土柱和核心筒中的一对控制点CB1和PIER1，如图3所示，得到了在结构封顶一年后的竖向变形。

通过计算，得到外框架柱和核心筒的竖向变形量及差异，如图4所示。由图可知，由于各压缩变形积累效应，竖向位移沿着高度总体上服从逐渐增大的规律，最大竖向位移发生在结构顶部103 mm。外框架柱CB1和核心筒剪力墙PIER1的总变形量及差异逐层递增，最大变形差为13.5 mm，严重影响了楼板的平整度，因此对其构件进行预调整是非常有必要的。

图3 竖向变形计算点Fig.3 Calculation points of vertical deformation

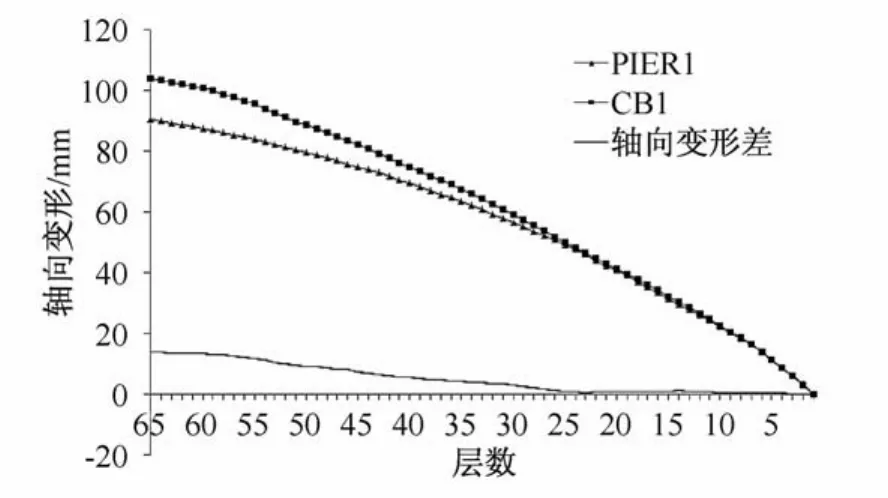
图4 竖向变形量及差异Fig.4 Vertical deformation and differences

核心筒和外框架柱的弹性、徐变和收缩变形分别如图5和图6所示。

图5 核心筒PIER1的竖向变形量Fig.5 Vertical deformation of core wall PIER1

由图可知，核心筒顶层PIER1的徐变和收缩变形量和占总变形量的47%，外框架柱CB1的徐变和收缩变形量和占总变形量的32%，因此在超高层设计时必须考虑徐变、收缩等非荷载作用下的变形。

图6 CB1柱的竖向变形量Fig.6 Vertical deformation of column CB1

4.2 下料长度调整

对于超高层建筑，已完成的竖向构件会随着施工的进行而不断发生竖向变形，应考虑竖向变形而进行预调整，可以简化施工过程中的调整。依据收缩和徐变的发展速度，可以确定施工完成一年后的轴向压缩补偿量。图7和图8分别为核心筒PIER1和外框架柱CB1下料长度的预调整量，也就是施工相应楼层时估算的竖向变形量。

图7 核心筒PIER1的竖向预调整量Fig.7 Vertical adjustment of core wall PIER1

图8 CB1柱的竖向预调整量Fig.8 Vertical adjustment of column CB1

4.3 施工阶段构件验算

各阶段仅在其已施工完成的部分添加重力荷载以及40%之活荷载模拟其施工荷载。第五阶段（伸臂合龙前）施加70%之50年重现期的风荷载。施工过程分析选取其中最为不利的荷载组合进行分析。

1）外框架柱

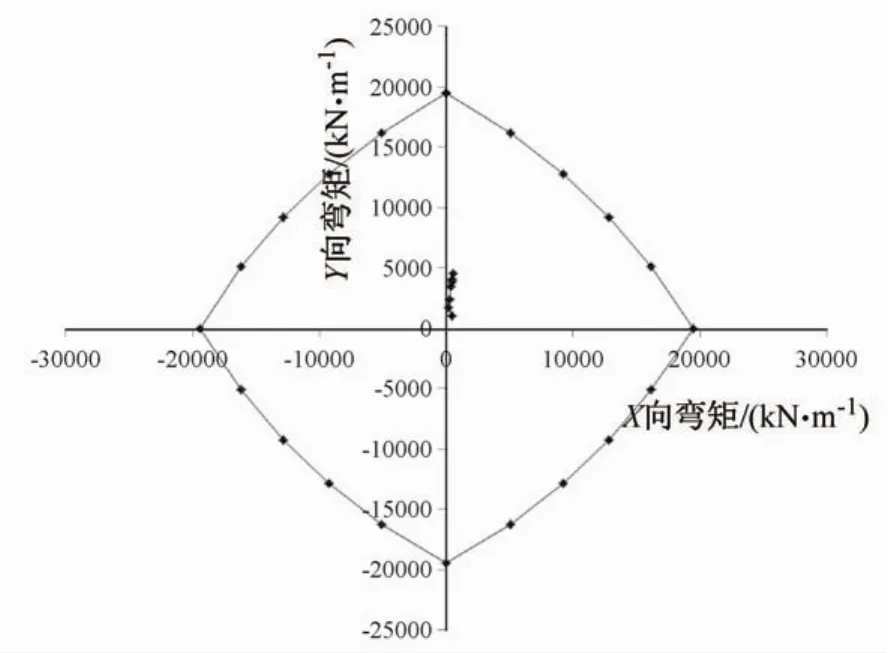
图9 柱CB1施工阶段内力校核Fig.9 Internal bearing capacity check of column CB1 in construction stages

由图10施工过程中外框架柱的承载力校核可知，外框架柱均能满足承载力要求。

2）外框钢梁、伸臂桁架与环向桁架

由图10可知，外框钢梁、伸臂桁架与环向桁架的最大应力为141 MPa，不超过钢结构Q345的设计值，均能满足承载力要求。

4.4 施工次序对水平伸臂构件内力影响

为避免外框架柱与核心筒之间的竖向变形差在伸臂桁架中产生较大次内力，在设定施工次序时伸臂桁架先临时固定，等结构封顶后再最终固定，这样封顶前其变形差不在伸臂桁架中产生内力，如图11所示。

图10 外框钢梁及伸臂桁架应力图Fig.10 Stress diagram of the outside box beam and cantilever truss

图11 伸臂桁架的临时固定Fig.11 Temporary fasten of the cantilever truss

由表1可知，后连接相比一次性加载考虑伸臂桁架在结构封顶后再形成刚性节点，构件内力可以卸载25%以上。

表1 考虑后连接伸臂桁架内力对比Table 1 Cantilever truss internal force comparison connsidering connection after construction

通过施工模拟分析，考虑结构封顶后伸臂桁架连接，可以有效地减少由于重力荷载作用下结构变形在伸臂桁架产生的内力，因此采用后连接的施工措施是必要的。

5 结 论

依据欧洲规范EC2关于混凝土弹性模型、收缩、徐变随时间变化的规定，考虑施工顺序加载、竖向构件压应力差异、水平伸臂桁架后连接、下料长度调整等因素，对某超高层建筑进行施工全过程分析，可以得到以下结论：

（1）竖向位移及差异沿着高度总体上服从逐渐增大的规律，最大竖向位移发生在结构顶部；

（2）核心筒与外框架柱竖向变形差异较大，严重影响楼板的平整度，必须对其构件进行预调整；

（3）核心筒和外框架柱徐变和收缩变形量和占总变形量的32%以上，在超高层设计时必须考虑非荷载作用下的变形；

（4）施工过程分析时应选取其中最为不利的荷载组合对外框架梁柱、伸臂桁架、环向桁架进行承载力验算；

（5）考虑结构封顶后伸臂桁架再连接工艺，可以有效地减少由于重力荷载作用下结构变形在伸臂桁架产生的内力。

［1］ 赖寒，何志军，丁洁民.上海中心大厦考虑施工过程的竖向变形及差异分析与研究［J］.结构工程师，2011，27（6）：14-21.Lai Han，He Zhijun，Ding Jiemin.Analysis and research of vertical deformation difference of Shanghai Tower considering construction process［J］.Structural Engineers，2011，27（6）：14-21.（in Chinese）

［2］ 任瑞，刘冰.超高层混合结构考虑施工过程的竖向变形差异计算和分析［J］.结构工程师，2013，29（2）：56-62.Ren Rui，Liu Bing.Vertical deformation difference analysis of super high-rise hybrid structures considering construction process［J］.Structural Engineers.2013，29（2）：56-62.（in Chinese）

［3］ 范峰，王化杰，支旭东.上海环球金融中心施工竖向变形分析［J］.建筑结构学报，2010，31（7）：118-124.Fan Feng，Wang Huajie，Zhi Xudong.Analysis of vertical deformation during construction of the ShanghaiWorld Financial Center［J］.Journal of Building Structures，2010，31（7）：118-124.（in Chinese）

［4］ 李烨，王建，周建龙.超高层建筑施工模拟分析的非荷载效应应用研究［J］.建筑结构，2012，42（5）：159-163.LiYe，Wang Jian，Zhou Jianlong.Applying research on construction simulation analysis of non-load effect of high-rise building［J］.Building Structure，2012，42（5）：159-163.（in Chinese）

［5］ 方辉.高层混合结构考虑施工过程和混凝土徐变收缩影响分析［D］.长沙：湖南大学，2006.Fang Hui.Analysis of tall hybrid-structureswith construction process creep and shrinkage effects［D］.Changsha：Hunan University，2006.（in Chinese）

［6］ 中华人民共和国住房和城乡建设部.JGJ 3—2010.高层建筑混凝土结构技术规程［S］.北京：中国建筑工业出版社，2010.Ministry of Housing and Urban-Rural Developmentof the People’s Republic of China.JGJ3—2010 Technical specification for concrete structures of tall building［S］.Beijing：China Architecture and Building Press，2010.（in Chinese）

［7］ 王光远.论时变结构力学［J］.土木工程学报，2000，33（6）：105-108.Wang Guangyuan.On mechanics of time-varying structures［J］.China Civil Engineering Journal，2000，33（6）：105-108.（in Chinese）

［8］ EC2：EN1992-1-1（2002）：Design of concrete structures［S］.The European Committee for Standardization，1992.

［9］ ACICommittee 209.Prediction of creep，shrinkage and temperature effect in concrete structure［S］.A-merican Concrete Institute，1992：15-21.

［10］ CEB-FIP Model code 1990：Design Code，Thomas Telford，1990.

Effect Analysis on the Vertical Deformation During Construction W hole Process of Super High-rise Building Structures

MA Yueqiang1，2，*
（1.Shanghai Second Construction Group Co.Ltd.，Shanghai200080，China；2.Shanghai Center of Top-Down Method in Construction Engineering，Shanghai200080，China）

According to European code EC2 about concrete elastic model，shrinkage and creep change over time and considering the construction order of loads，the difference of the vertical compressive stress components，cantilever truss connections and blanking length adjustment，The paper realized the whole construction process simulation in combination with a super-high building structure and obtained the results of the total vertical deformation and the relative deformation between the outer frame and the core-wall.At the same time，it calculated the bearing capacity of key components in every construction stages and compared the internal forces of the horizontal cantilever truss considering connection after construction.Analysis results show that concrete shrinkage and creep deformationmustbe considered for the design of high-rise building structure，the deformation of the vertical component of vertical deformation should be considered to adjust，and the internal force of horizontal cantilever truss could be reduced through connection after construction.

super high-rise structures，construction whole process，vertical deformation，adjustmentof cutting length，connection after construction

2013－11－18

*联系作者，Email：yqma1982＠163.com