裂隙岩体岩石质量指标（RQD）的空间变化特征

李继明，左三胜

1.义乌工商职业技术学院建筑与艺术分院，浙江 义乌 322000

2.成都理工大学环境与土木工程学院，成都 610059

0 引言

岩石质量指标（RQD）是评价岩体破碎程度的一个重要参数。Deere［1］首次提出了RQD的概念，即采用75mm直径的金刚石钻头和双层芯管在岩石中连续取芯，岩芯长度大于10cm的累积长度与进尺的比值，以百分比表示。迄今为止，RQD已被广泛地用来评价岩体的稳定性及对岩体的等级进行分类［2－4］。工程上获取岩体的RQD常用钻孔法，这种方法因需要通过钻探获取岩芯，这样既费时又不经济，并且只能获取竖直方向或近竖直方向上的RQD。而测线法相对于钻孔法而言，省略了钻孔这一步骤，可获得不同方向上的RQD［5－6］。但岩土工程师们在利用测线法计算RQD的过程中，往往忽略了测线长度和测线方向的影响，而直接根据与测线相交的节理间距来计算。

RQD值与裂隙频率密切相关。裂隙频率越大，则节理愈发育，RQD值越小。因此裂隙频率在空间的变化一定程度上能够反映RQD在空间的变化。Hudson等［7］在1983年提出了裂隙频率随测线方向变化的观点，并给出了裂隙频率变化的二维平面图。测线长度对RQD的影响目前鲜有研究。Priest等［8］认为随着测线长度的变化，RQD是不断增大的，并提出了RQD随测线长度变化的经验公式。之后，Senz等［9］在其基础之上改进该公式，改进后的公式所得RQD值更接近实际值。张文等［10］通过在建立的三维裂隙网络模型中布置不同长度的测线来研究RQD的尺寸效应，并提出了3种RQD的计算模型。

通过三维裂隙网络模拟的方法，可以研究RQD空间的各向异性特征等，但过程较为复杂，计算量巨大。笔者试图寻求一种简单的方法，通过二维平面中简单易取的裂隙来进行整个三维空间的RQD分析。即以野外的岩石露头这个二维的平面上得到的节理的起点坐标、终点坐标与产状等为基础，通过推导得到三维空间中任意方向的RQD。此外，通过蒙特卡罗模拟产生不同裂隙频率的节理间距，来研究节理密集程度不同下的RQD随测线长度的变化规律，以期为今后确定测线法获取RQD的合理测线长度提供理论依据。

1 RQD随测线方向的变化

1.1 概况

Priest［11］提出，沿着某一测线方向的RQD与节理的频率有关，并给出了RQD的估算公式：

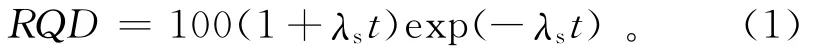
式中：λs为沿着该方向测线的裂隙频率，m－1；t为阈值，m。常规RQD的阈值采用0.1m。

由式（1）可知，在阈值一定的情况下，某一测线方向的RQD仅与裂隙的频率有关，与测线的长度无关。

Hundson和Priest在1979年曾经证明n组节理沿着任意方向测线的裂隙频率可通过式（2）计算［12］：

式中：λi为第i组节理沿其法线方向的频率，即该组节理的裂隙频率，其值为第i组节理间距的倒数；θsi为测线与第i组节理的法线方向所夹锐角。

当已知各个节理组的产状及节理间距时，可以由公式（1）和公式（2）推导出三维空间中任意方向的RQD。而节理组的产状及节理间距很容易从野外或隧道中的岩石露头上获取。

此外，笔者根据已知方向的RQD值及各节理组的产状推导得出三维空间中任意方向的RQD。其推导过程如下：

已知某岩石露头上m条不同方向测线所得的RQD值，即RQD1、RQD2、…、RQDm，及各个节理组的产状（包含临空面那组节理），则在阈值一定的情况下可根据公式（1），求得沿测线方向的裂隙频率λs1、λs2、…、λsm。根据公式（2）可得以下方程：

式中，θsim为第m条测线与第i组节理的法线方向所夹锐角。

由公式（3）可知，已知方向的RQD值的个数需大于等于节理组数，即m≥n，方程组才有解。解上述方程组则可得到各组节理的裂隙频率λi，则通过公式（1）及公式（2）便可得到三维空间中任意方向的RQD。

由此可见，利用二维平面上简单、易于获得的节理参数可得到三维空间中任意方向的RQD，且相对于三维网络模拟来说，方法简便、易理解且计算量小。

1.2 RQD 估算

以浙江省内芦岭岩质边坡为工程依托，研究RQD随测线方向的变化规律。该边坡处于滨海平原与低山丘陵交界处，山高坡陡；该区域属于亚热带季风气候，四季分明，温暖湿润，雨量丰沛；该边坡地表水不发育，地下水以基岩裂隙水为主；该地区地层岩性单一，以侏罗纪强风化晶屑凝灰岩为主，全风化层极薄，0.1m左右，强风化层厚10.0～13.0m，节理较发育，岩石破碎。

根据陈剑平等［13－14］的节理起点坐标的选取原则，笔者在现场取迹长大于0.5m的89条节理的起点坐标、终点坐标与产状等，绘二维迹线如图1所示。将节理分成3组，其参数如表1所示。其中节理间距在现场测量后经产状校正后获得。将迹长小于0.5m的节理包含在内。

图1 二维迹线图Fig.1 Two-dimensional trace map

由表1及公式（2）可得到沿某方向测线裂隙频率λs，进而根据公式（1）得到该测线方向的RQD。测线的方向由2个要素来决定，即倾伏向α和倾伏角β，其含义与地质学中线状构造产状的倾伏向和倾伏角相同，即倾伏向α指测线在水平面上的投影线向下倾伏一端的方位，其取值为0°≤α＜360°，倾伏角β指测线与其在水平面上的投影线之间的夹角，其取值为0°≤β≤90°。为研究RQD在整个空间中的变化规律，本文以1°的变化量改变测线的倾伏向和倾伏角，共产生360×91条测线，通过上述方法得到360×91个对应的RQD值。计算得到不同测线方向所对应的RQD等值线图（图2），图2线条上的数字代表相应的RQD值。本文中阈值t采用常规的0.1m。该计算过程通过商业软件MATLAB实现。

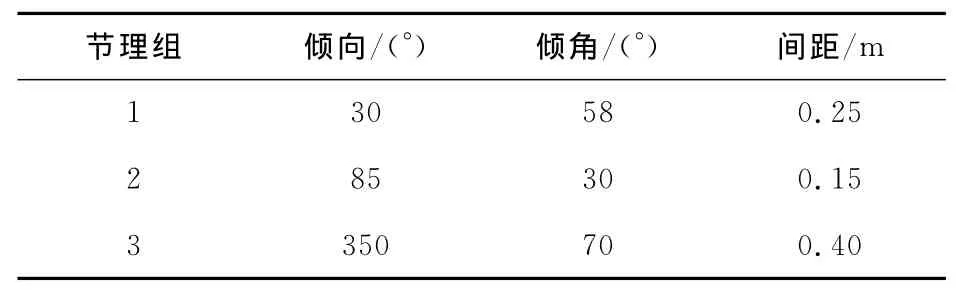
表1 3组节理参数Table 1 Parameters of three fracture sets

1.3 结果分析

图2中，倾伏角β为90°时所对应的RQD值，可相当于通过垂直钻孔得到的RQD，由计算结果可知，倾伏角β为90°时的RQD值为78.17%，而现场的3个垂直向钻孔岩芯的RQD分别为75%、76%和80%，可见通过1.1节中的方法来计算RQD值是合理的。通过图2可知，RQD随着测线的产状变化而变化。同时发现图中存在2个明显的极值点。结合计算结果可知：极小值点处测线的α为220°，β为51°，RQD值为68.67%；极大值点处测线的α为100°，β为29°，RQD值为99.39%。所以测线方向的布设对于获取RQD值具有重要意义，不同的测线方向将得到不同的RQD，说明测线法获得的RQD在空间中具有各向异性。

由上述分析可知，岩体RQD是各向异性的。因此，利用与工程所关注的方向不同的测线获取RQD进行工程设计是不可取的。在利用RQD设计时，应布置与工程所关注的方向相同的测线来获取RQD，或者对钻孔得到的RQD进行方向上的校正。如果无法在岩石露头上布置与工程所关注的方向相同的测线，可根据1.1节中的方法利用其他方向的RQD推导得到该方向的RQD。

2 RQD随测线长度的变化规律

在实际工程中，利用钻孔资料或测线法计算RQD时，通常会忽略钻孔进尺或测线长度对RQD值的影响。事实上，并非任意的钻进尺寸或测线长度都能获 得 岩 体 的 真 实RQD值［15－16］。此 外，节 理发育程度不同时，钻进尺寸或测线长度对RQD的影响是否相同，也不得而知。因此，笔者在测线法的基础上，利用计算机模拟来研究二维条件下RQD随测线长度的变化规律，为今后在隧洞或野外露头上利用测线法获取精确的RQD确定合理的测线长度提供一定的理论依据。为实现对RQD的整体研究，笔者除了对工程分析的裂隙频率研究外，还研究了不同裂隙频率下，RQD随测线长度的变化规律，来代表节理发育不同密集程度下测线长度对RQD值的影响。

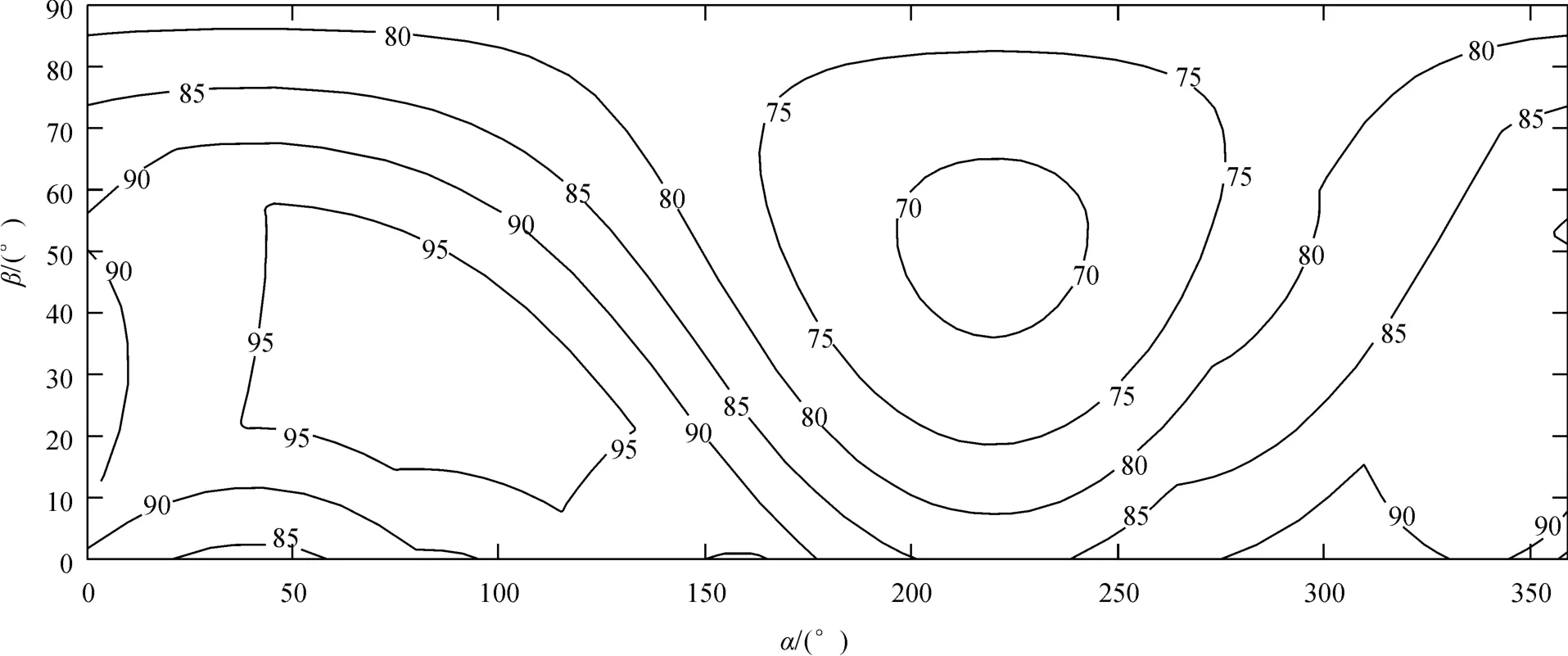
图2 不同测线方向所对应的RQD等值线图Fig 2 RQDContour diagrams varied with scanline orientation

2.1 计算模型的建立

图3 测线与节理相对位置示意图Fig.3 Diagram of relative position between scanline and fractures

在测线法计算RQD值中，如图3所示测线的起点并不是不一定恰与天然节理相交，因此张文等［10］根据Priest［11］提出的2种RQD的计算模型进行延伸，根据测线的端点与裂隙的相对位置关系，在三维裂隙网络的基础上建立了3种RQD的计算模型，即 A-A、T-T、A-A-S模型，讨论不同阈值下RQD随测线长度的变化规律。其中A-A、T-T、A-A-S模型的具体介绍见文献［10］中6.1节，在此不再赘述。3个模型中都涉及首段长，即假设测线的起点不与节理相交，但未考虑测线起于节理的情况，为了理论的严密性，笔者提出第4种RQD计算模型，即N-A模型。N-A模型特点如下：假定测线起于天然节理；将末段长L2考虑到RQD的计算中。该模型弥补了其他3种模型未考虑测线起于节理的不足，因测线起于节理在现场测量时是常见的形式。N-A模型的计算公式为

式中：L为测线长度；Lt为节理间距大于阈值t的累计长度。

2.2 计算机模拟

通过文献［10］中 Senz-Kazi与 Priest-Hudson公式，可知RQD的值与裂隙频率λ、阈值t及测线长L有关。因此笔者在常规阈值t＝0.1m的条件下，研究不同裂隙频率时RQD随测线长度的变化规律。其模拟步骤如下：

1）确定裂隙频率λ

为使研究的裂隙频率范围较大，确定的裂隙频率为2.5，5.0，7.5，10.0，12.5，15.0m－1。

2）确定测线L的变化范围

当阈值t＝0.1m时，测线长度小于0.2m的意义不大，因此确定测线长度的变化范围为0.2～20.0m，测线长度的增量为0.2m。

3）蒙特卡罗模拟

假设不连续岩体是统计均匀的，即裂隙频率在统计上设定是均匀的，并且节理间距服从负指数分布［17－18］，即f（x）＝λe－λx。在基于上述假设的基础上，利用蒙特卡罗模拟产生服从负指数分布的随机数代表节理间距值，以此来计算RQD。然后，通过改变负指数分布函数的参数λ来产生不同裂隙频率的节理间距值。为消除统计上的偶然性，在每个裂隙频率下都生成256组数据，每组数据包含550个节理间距值以供选用。

4）RQD模拟计算

利用蒙特卡罗模拟产生的随机节理间距值，利用自编的程序进行计算4种模型下的RQD值，每个模型在每个裂隙频率及每个测线长度下均产生256个RQD值。

通过上述4个步骤，可得到在不同裂隙频率下、不同测线长度在4种计算模型下所对应的RQD值。

2.3 结果分析

根据上述4种模型计算所得结果，取不同裂隙频率下各个测线长度下的RQD均值，做出RQD均值随测线长度的变化图，如图4所示。根据不同裂隙频率下各个测线长度下的RQD标准差做出RQD标准差随测线的长度的变化图，如图5所示。

图4 RQD均值随测线长度的变化Fig 4 Variation of mean of RQDvalues with the scanline length

首先，从图4可知：各个计算模型都随着测线长度的增大而收敛，因此，越长的测线能得到越精确的代表岩体质量的RQD值。当假定公式（1）所得RQD值为特定裂隙频率下RQD的代表值时，则各个计算模型收敛时的测线长及收敛的RQD值如表2所示。由表2可以看出：4种计算模型中，T-T模型的收敛值与公式（1）的差别最大；N-A和A-A模型次之；A-A-S模型收敛时的RQD更接近公式（1）的值。通过几种计算模型对比可以得出，测线较短时，A-A-S模型得到的RQD值，相对于其他3种计算模型更精确。各个计算模型的收敛速度不同：TT模型的收敛速度最慢；N-A和A-A模型次之；AA-S模型收敛速度最快。并且随着裂隙频率的增加，T-T模型的收敛速度变快，而N-A和A-A模型的收敛速度变慢，A-A-S模型的收敛速度基本不变。

其次，在测线较短，特别是小于1.0m时，AA-S模型所得到的RQD更接近于收敛时的RQD；而其他模型在测线较短时，与收敛时的RQD差别较大。故在今后的工程中，如果岩石露头区域较小，无法布置较长测线时，可以选用A-A-S模型来获得岩体的RQD，这样更接近与岩体真实的RQD值。

另外，由图5可以发现，4种计算模型所得的RQD的变化率都随着测线长度的增大而减小。这说明越长的测线可以得到越可信的RQD值。例如，当变化率小于0.5%时，不同裂隙频率下所需要的最小测线长度如表3所示。可以发现，除T-T模型外，其余3种模型最小测线长度都随着频率的增加而增加。经过拟合，3种模型中裂隙频率λ与最小测线长Lmin之间的关系式如下。

上述可知，要得到可信度相同的RQD值，则在越大的裂隙频率所需要的最小测线长越长。即在节理较发育的地方，也是工程上特别关心的地方，适当增加测线长度可以得到更加可信的RQD值。

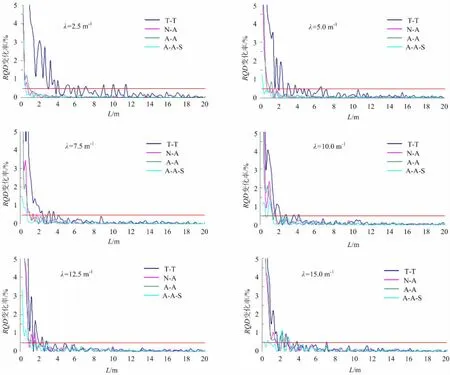
图5 RQD变化率随测线长度的变化Fig 5 Variation rate of RQDvalues with the scanline length

表2 不同模型下收敛测线长与收敛RQD值Table 2 Convergence scanline lengths and convergence RQDvalues under different models

表3 RQD变化率小于0.5%时的最小测线长Table 3 Minimum scanline length required for less than 0.5%in variation rate of RQD

3 结论

测线法估算RQD值时，不同的测线方向和长度对估算的RQD具有明显的差异。笔者对RQD随测线方向和长度的变化进行了模拟，得出以下结论：

1）利用岩石露头，即二维平面上的RQD或从该平面上获取的节理产状及间距数据可推导得出三维空间中任意方向的RQD。

2）RQD随着测线的产状变化而变化，RQD在空间具有各向异性。不同产状的测线得到的RQD值不同。在工程上应尽量选用与工程所关注的方向相同的测线所得的RQD来进行设计。

3）测线倾伏向相同时，即相当于在直立的岩石露头上布置测线，RQD值随着倾伏角的变化而变化，RQD在平面中也具有各向异性。

4）提出的 N-A 模型弥补了 T-T、A-A、A-A-S模型未考虑测线起于节理的不足，使理论论证更加严密。

5）4种计算模型T-T、N-A、A-A、A-A-S都随着测线的长度的增大而收敛，即越长的测线越能得到精确的RQD值。但收敛速度不同：T-T模型的收敛速度最慢；N-A和 A-A模型次之；A-A-S模型收敛随度最快。

6）在测线较短，特别是小于1.0m 时，A-A-S模型所得到的RQD更接近于收敛时的RQD。在无法布置较长的测线的露头上估算RQD值时，选用A-A-S模型可得到相对精确的RQD值。

7）4种计算模型所得的不同测线长度下RQD值的变化率都随着测线长度的增大而减小，越长的测线可以得到越可信的RQD值，故在工程上特别关心的地方，即节理较发育的地方，适当加长测线长度可得更加可信的RQD值。

（

）：

［1］Deere D U.Technical Description of Rock Cores for Engineering Purposes ［J］. Rock Mechanics and Engineering Geology，1963，1（1）：18-22.

［2］王吉亮，陈剑平，杨静.距离判别法在公路隧道围岩分类中的应用［J］.吉林大学学报：地球科学版，2008，38（6）：999-1004.

Wang Jiliang，Chen Jianping，Yang Jing.Application of Distance Discriminant Analysis Method in Classification of Surrounding Rock Mass in Highway Tunnel［J］.Journal of Jilin University：Earth Science Edition，2008，38（6）：999-1004.

［3］邱道宏，陈剑平，阙金声，等.基于粗糙集和人工神经网络的洞室岩体质量评价［J］.吉林大学学报：地球科学版，2008，38（1）：86-91.

Qiu Daohong，Chen Jianping，Que Jinsheng，et al.Evaluation of Tunnel Rock Quality with Routh Sets Theory and Artificial Neural Networks［J］.Journal of Jilin University：Earth Science Edition，2008，38（1）：86-91.

［4］周念清，杨楠，汤亚琦，等.基于Hoek-Brown准则确定核电工程场地岩体力学参数［J］.吉林大学学报：地球科学版，2013，43（5）：1517-1522.

Zhou Nianqing， Yang Nan， Tang Yaqi，et al.Determination of Rockmass Mechanical Parameters of Nuclear Power Engineering Site Based on Hoek Brown Criterion［J］.Journal of Jilin University：Earth Science Edition，2013，43（5）：1517-1522.

［5］Zhang W，Wang Q，Chen J P，et al.Determination of the Optimal Threshold and Length Measurements forRQDCalculations［J］.International Journal of Rock Mechanics and Mining Sciences，2012，51：1-12.

［6］Zhang W，Chen J P，Cao Z X，et al.Size Effect ofRQDand Generalized Representative Volume Elements：A Case Study on an Underground Excavation in Baihetan Dam，Southwest China［J］.Tunneling and Underground Space Technology，2013，35：89-98.

［7］Hudson J A，Priest S D.Discontinuity Frequency in Rock Mass ［J］.International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts，1983，20（2）：75-89.

［8］Priest S D，Hudson J A.Discontinuity Spacing in Rock［J］.International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts，1976，13（5）：135-148.

［9］Senz Z，Kazi A.Discontinuity Spacing and RQD Estimates from Finite Length Scanlines ［J］.International Journal of Rock Mechanics and Mining Sciences and Geomechanics Abstracts，1984，21（4）：203-212.

［10］张文，陈剑平，苑晓青，等.基于三维裂隙网络的RQD尺寸效应与空间效应的研究［J］.岩石力学与工程学报，2012，31（7）：1437-1445.

Zhang Wen，Chen Jianping，Yuan Xiaoqing，et al.Study of Size Effect and Spatial Effect ofRQDfor Rock Masses Based on Three-Dimensional Fracture Network［J］.Chinese Journal of Rock Mechanics and Engineering，2012，31（7）：1437-1445.

［11］Priest S D.Discontinuity Analysis for Rock Engineering［M］.London：Chapman ＆ Hall，1993.

［12］陈剑平，肖树芳，王清.随机不连续面三维网络计算机模拟原理［M］.长春：东北师范大学出版社，1995：216-220.

Chen Jianping，Xiao Shufang，Wang Qing.Three-Dimensional Network Modeling of Structure Fractures［M］. Changchun： Northeast Normal University Press，1995：216-220.

［13］陈剑平，石丙飞，王清.工程岩体随机结构面优势方向的表示法初探［J］.岩石力学与工程学报，2005，24（2）：241-245.

Chen Jianping，Shi Bingfei，Wang Qing.Study on the Dominant Orientations of Random Fractures of Fractured Rock Masses［J］.Chinese Journal of Rock Mechanics and Engineering，2005，24（2）：241-245.

［14］陈剑平，王清，赵红亮.窗口测线法获取岩体RQD［J］.岩石力学与工程学报，2004，23（9）：1491-1495.

Chen Jianping， Wang Qing，Zhao Hongliang.ObtainingRQDof Rock Mass by Sampling Window Method［J］.Chinese Journal of Rock Mechanics and Engineering，2004，23（9）：1491-1495.

［15］Zhang W，Chen J P，Liu C，et al.Determination of Geometrical and Structural Representative Volume Elements at the Baihetan Dam Site［J］. Rock Mechanics and Rock Engineering，2012，45：409-419.

［16］Zhang W，Chen J P，Wang Q，et al.Investigation of RQD Variation with Scanline Length and Optimal Threshold Based on Three-Dimensional Fracture Network Modeling［J］.Science China Technology Sciences，2013，56：739-748.

［17］杜时贵，王思敬.岩石质量指标（RQD）的方向异性分析［J］.工程地质学报，1996，4（4）：48-54.

Du Shigui，Wang Sijing.Anisotropy Analysis of Rock Quality Index （RQD）［J］.Journal of Engineering Geology，1996，4（4）：48-54.

［18］Zhang W，Chen J P，Yuan X Q，et al.Network Modeling and Stochastic Mathematics Analysis of RVE Size Based on Three-Dimensional Fracture Numerical［J］.Quarterly Journal of Engineering Geology and Hydrogeology，2013，46：31-40.