独立钢丝绳芯钢丝绳应力及变形分布

吴 娟,寇子明,刘玉辉,吴国雄

(1．太原理工大学机械工程学院,山西太原 030024;2．山西省矿山流体控制工程(实验室)技术研究中心,山西太原 030024)

独立钢丝绳芯钢丝绳应力及变形分布

吴 娟1,2,寇子明1,2,刘玉辉1,2,吴国雄1,2

(1．太原理工大学机械工程学院,山西太原 030024;2．山西省矿山流体控制工程(实验室)技术研究中心,山西太原 030024)

以右交互捻钢丝绳为例,在一次螺旋线空间方程的基础通过Frenet-Serret标架上推导出二次螺旋线空间矢量表达式。构建了14-6×36WS-IWRC-sZ和14-6×36WS-IWRC-zZ两种钢丝绳有限元分析模型。采用Augmented-Lagrangian算法,分析两种捻向钢丝绳外股层钢丝应力及变形分布规律。研究结果表明:钢丝的捻制方式和空间位置对股内钢丝的应力及变形影响很大;右交互捻和右同向捻钢丝绳二次捻制钢丝的等效应力呈现不均匀分布,钢丝的最大等效应力随着曲率的变化而变化;右交互捻和右同向捻钢丝绳变形基本相同,同层钢丝变形呈现抛物线分布且绳股中离绳芯较近钢丝的变形均大于同层其它钢丝;右同向捻钢丝绳股内钢丝应力、变形及钢丝之间的错动量幅值均大于右交互捻钢丝绳。并进行14-6×36WS-IWRC-sZ钢丝绳拉伸试验,在误差允许范围内,试验结果与模拟结果基本吻合,验证了模型的正确性。

独立绳芯;多股层;应力及变形分布;有限元法

矿井摩擦提升钢丝绳常使用6×36WS-IWRC钢丝绳。提升过程中,提升钢丝绳承受拉伸、扭转、弯曲等载荷作用。在绳端载荷和自重作用下,钢丝绳既承受拉力又发生扭转。拉伸和扭转时由于钢丝在绳中所处位置不同,钢丝变形也不相等,钢丝绳内钢丝应力会重新分布。而钢丝在钢丝绳中起承载作用,钢丝的力学性能会对整个钢丝绳的力学性能产生决定性的影响[1]。

以6×36WS-IWRC钢丝绳为研究对象(图1)。该绳由独立钢丝绳芯和外股层组成。独立绳芯为6× 7IWRC,由中心股和内股层组成。外股层有右交互捻和右同向捻两种捻制方式。中心股侧丝、内股层股芯丝和外股层股芯丝为一次捻制而成,内股层侧丝和外股层侧丝均为二次捻制钢丝。

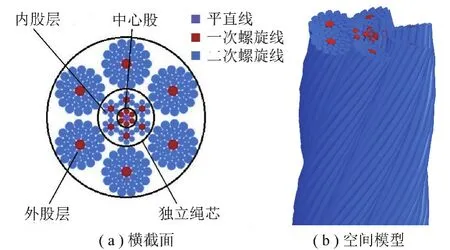
图1 6×36WS-IWRC钢丝绳Fig．1 6 strand warrington-seale rope

近年来有限元法在钢丝绳研究领域有较广泛的应用。国内外学者建立了单捻钢丝绳有限元分析模型[2-7],分析在轴向载荷作用下单捻钢丝绳的性能特性。C．Erdonmez[8]建立了6×7IWRC钢丝绳数学模型,分析在不同载荷下钢丝绳绳芯的应变,并进行了试验验证。马军等[1]建立钢丝绳芯(6×19IWS)的有限元模型,分析绳芯内钢丝的载荷分布。王大刚[9-10]建立6×19IWS钢丝绳有限元模型,对钢丝微动磨损和疲劳寿命进行了有限元分析。D．Elata等[11]建立了独立绳芯钢丝绳的数学模型,分析钢丝绳在轴向力和扭矩的作用下的动态特性。

前述成果中,利用有限元法分析独立钢丝绳芯外股层应力及变形分布的文献较少。本文利用有限元法,建立了完整的钢丝绳实体计算模型,分析在拉伸载荷的作用下钢丝绳外股层受力、变形及股内钢丝受力情况以及不同捻向对钢丝绳的性能的影响规律。

1 钢丝绳模型的建立

1.1 一次螺旋线与二次螺旋线空间方程

应用空间微分几何理论[12],假设一次螺旋线上的任意一点A用矢量R表示,A点处的Frenet-Serret标架ts-ns-bs如图2所示,ts为切向量,ns为主法向量,bs为副法向量,二次捻制的外层丝上任意一点B用矢量P表示。以右交互捻为例,通过转换矩阵T, P可由R与Q表示,那么二次捻制钢丝矢量表达式P=R+Q,如图3所示。一次螺旋线的缠绕半径和转角分别为rs和φs,二次螺旋线的缠绕半径、捻角和转角分别为rw,β和φw。

图2 空间曲线Frenet-Serret标架Fig．2 Frenet-Serret frame of space curves

图3 空间曲线矢量Fig．3 Space curves of single and double helical wire

一次螺旋线的矢量表达式为

切向量ts、主法向量ns和副法向量bs的参数表达为

1.2 三维实体模型

以14-6×36WS-IWRC钢丝绳为例,其结构数值参数见表1[13]。

利用Pro/E软件相应的螺旋线和螺旋扫描体等命令建立右交互捻钢丝绳和右同向捻钢丝绳两种模型,如图4所示。

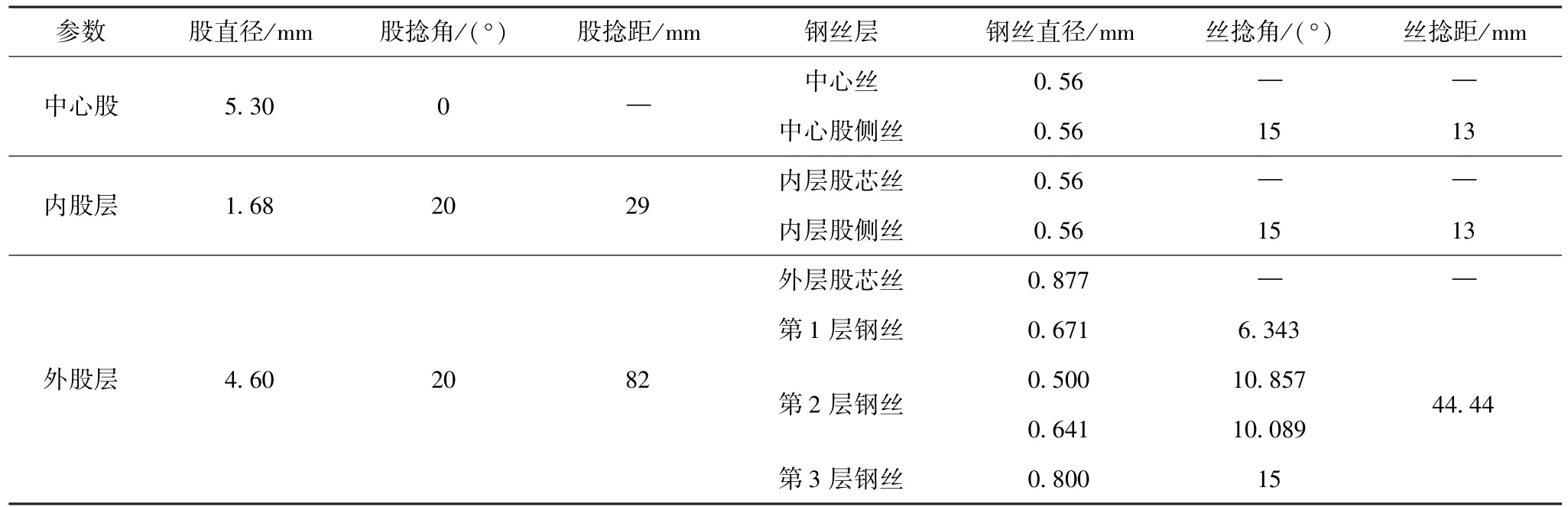
表1 14-6×36WS-IWRC钢丝绳结构参数[13]Table 1 Structure parameters of 14-6×36WS-IWRC rope[13]

图4 钢丝绳三维实体模型Fig．4 3D geometric models of rope

1.3 有限元模型及边界条件

钢丝绳中的钢丝材料通常为非合金碳素钢,此材料的弹性模量E=183．9 GPa,泊松比μ=0．3,剪切模量G=85．3 GPa,屈服极限σs=1．29 GPa。定义单元属性的类型为Solid187,取适当的精度等级和采用扫掠体网格划分方式划分网格,为了节省计算空间,截取绳的一个捻距作为研究对象,在分析软件ANSYS Workbench中生成有限元模型,单元数为275 124,节点数1 395 168。

一些学者曾做过忽略钢丝间摩擦效应,润滑良好的钢丝间的钢丝绳仿真的结果接近于实际[14]。本文在此假设的基础上,采用Splitting-pinball搜索法,接触载荷采用Augmented-Lagrangian算法计算,接触刚度取0．01,允许侵彻系数取0．2。同向捻和交互捻钢丝绳中钢丝之间的接触为线接触,目标面和接触面的接触形式如图5所示。在钢丝绳有限元模型的一端施加面载荷,在另一端施加面约束,限制x,y,z三个方向的所有自由度。

图5 钢丝接触模型Fig．5 Wire contact models

2 模拟仿真结果与分析

2.1 外股层钢丝应力分布

等效应力σe(equivalent stress)是第四强度理论上衡量材料屈服的强度准则,适用于钢丝绳这种塑性材料。当材料的屈服极限小于等于等效应力时,材料就进入塑性区域。其表达式[15]为

为了分析钢丝绳外股层内钢丝应力分布规律,将右交互捻钢丝绳外股层中每股沿逆时针方向编号,并取出右交互捻绳外股层中第1,2,4和5股钢丝作为研究对象,在整体坐标系中,右交互捻钢丝绳第1,2, 4和5股分别处于0°,60°,180°和240°相位。股中每层离股芯最近的钢丝用星号标识。在轴向载荷F1= 20 kN作用下,右交互捻钢丝绳中4股钢丝的等效应力如图6所示。

在整体坐标系中,沿逆时针方向,取出右同向捻钢丝绳外股层中相邻3股,分别编号为第1,2和3股,其相位差为60°。在轴向载荷F1=20 kN作用下,右同向捻钢丝绳中相邻3股钢丝的等效应力分布情况,如图7所示。

通过图6和图7可以看出:

(1)在右交互捻钢丝绳模型中,从等效应力分布来看,第1股钢丝应力分布和相位差180°的第4股钢丝应力分布对称;同样,第2股钢丝应力分布和相位差180°的第5股钢丝应力分布对称。每股中最大、最小等效应力均分布在靠近钢丝绳芯位置。

(2)在右同向捻钢丝绳模型中,相邻3股中每股钢丝的最大、最小等效应力呈现相似情况。相邻股钢丝的等效应力相位差为60°。

(3)在右交互捻和右同向捻钢丝绳中,二次捻制钢丝的等效应力呈现不均匀分布,这与二次捻制钢丝在股中的位置有很大关系,钢丝的最大等效应力随着曲率的变化而变化。右同向捻钢丝绳的钢丝应力大于右交互捻的。

(4)在钢丝绳模型加载端和约束端面上,由于存在约束效应和应力集中现象,端面处的等效应力要大于股内钢丝其他位置。由于绳股与股之间接触处外层丝周期性接触,外层丝的等效应力也呈现等值幅度波动。

2.2 外股层钢丝变形规律

每层标星号钢丝记为1,沿逆时针方向依次将每根钢丝标记为2,3,4,……,在局部坐标系中,第1,2层细钢丝的相位相同,标识星号1初相位为0°,相邻钢丝的相位差为51．43°;第2层粗钢丝的初相位为25．71°,相邻钢丝的相位差为51．43°;第3层钢丝的初相位为12．95°,相邻钢丝的相位差为25．53°。在轴向载荷F1=20 kN作用下,距绳约束端80 mm处钢丝绳第1,2,4和5股各层钢丝变形如图8所示。

同理,在轴向载荷F1=20 kN作用下,距绳约束端80 mm处,右同向捻钢丝绳外股层第1,2和3股各层钢丝变形如图9所示。

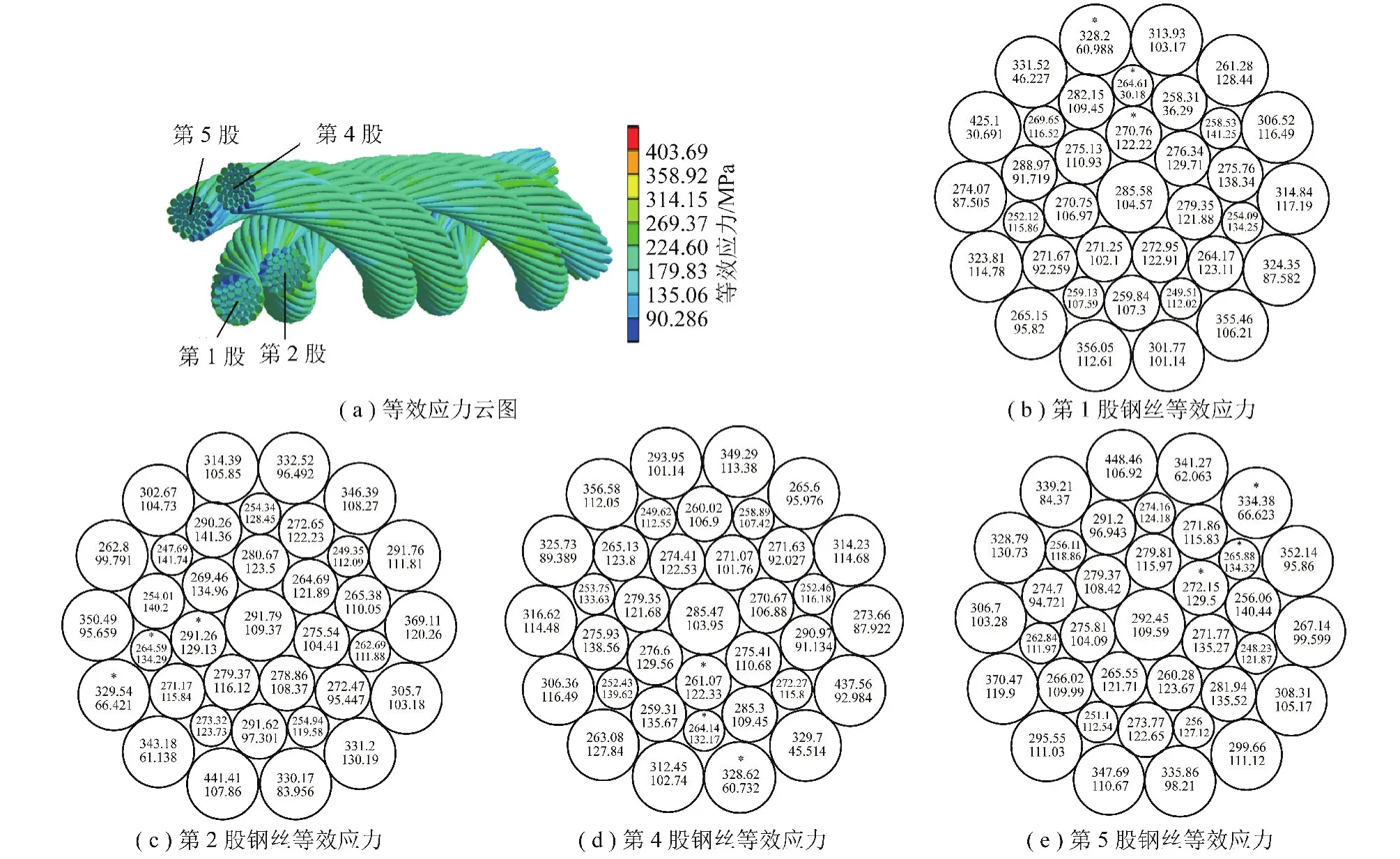
图6 右交互捻绳中4股钢丝等效应力分布(F1=20 kN)Fig．6 The maximum and minimum equivalent stress of each wire for four strands in the right regular lay rope at F1=20 kN

图7 右同向捻绳中3股钢丝的等效应力分布(F1=20 kN)Fig．7 Equivalent stresses of wires for three adjacent strands in the right lang lay rope when the loading force is F1=20 kN

图8 右交互捻绳4股各钢丝变形分布Fig．8 Deformations of wires in the right regular lay rope

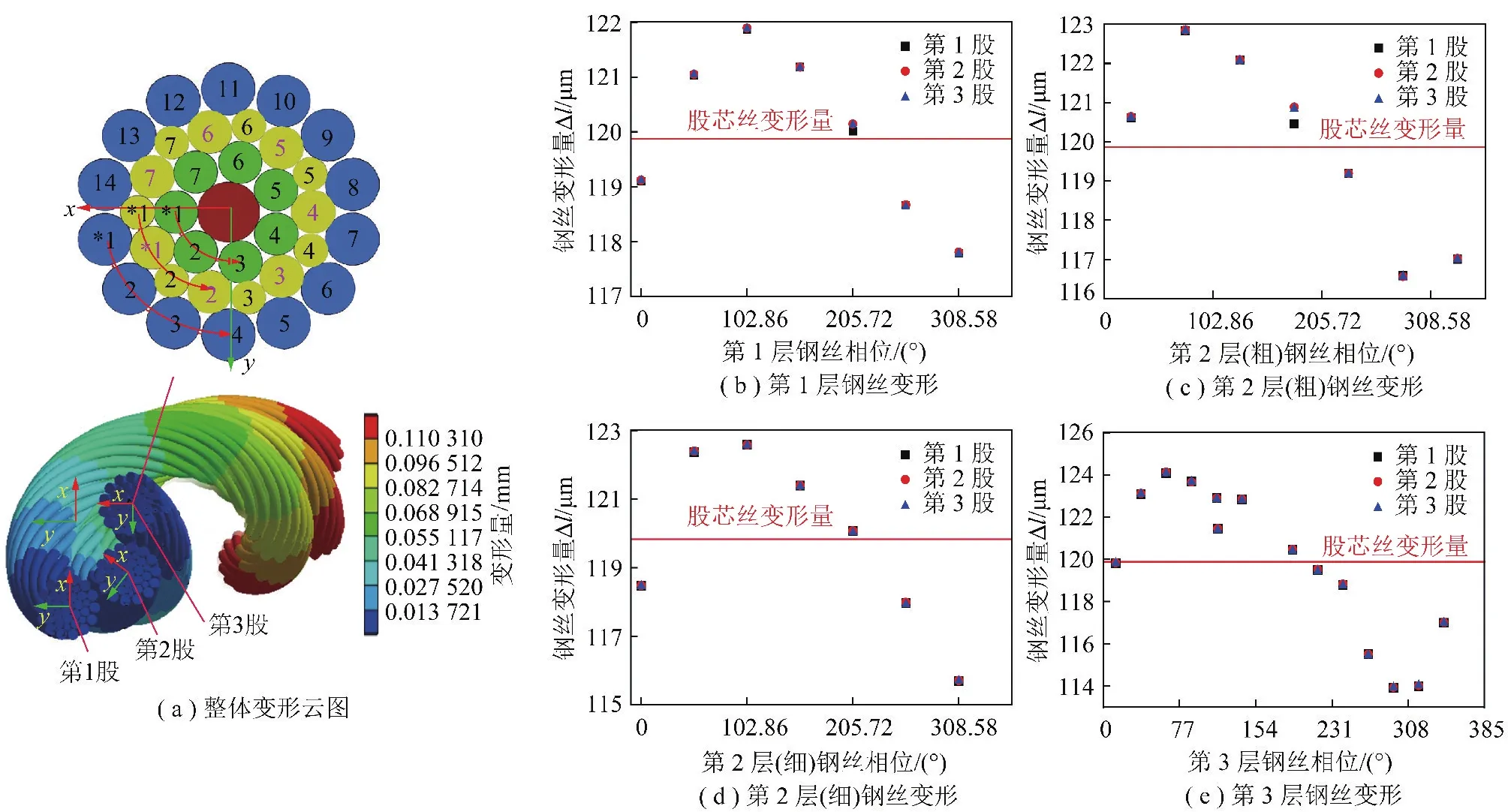
图9 右同向捻绳中3股钢丝变形分布Fig．9 Deformations of wires in the right lang lay rope

通过图8和图9可以看出:

(1)右交互捻钢丝绳4股变形基本相同,同层钢丝变形呈现抛物线分布。绳股中离绳芯较近钢丝的变形均大于同层其他钢丝。右同向捻钢丝绳中3股钢丝变形分布相似,变化规律同交互捻钢丝绳。但是,同向捻钢丝绳股内钢丝变形量大于右交互捻的。

(2)绳股钢丝层中靠近绳芯侧钢丝变形量大于股芯丝的,远离侧小于股芯丝,即绳股中相对于股芯一半处于拉伸状态,一半处于压缩状态。

(3)在两种钢丝绳模型中,一次螺旋线变形量基本相同。二次螺旋线变形与一次螺旋线的差值为两钢丝的相对错动量,同向捻钢丝绳钢丝错动量幅值明显高于交互捻的。

3 钢丝绳试验结果分析

利用WDW-100A型微机控制电子万能试验机对14-6×36WS-IWRC右交互捻钢丝绳施加拉伸载荷,采用套压法试样制备夹持绳端。为了便于测量钢丝绳变形伸长的微小位移,采用BCX5000型变形测量显示仪作为测量仪器,其标距为500 mm,量程为10 mm。试样的处理过程为:首先检查合格试样并截取600 mm长度,将试样两端穿入铝合金套管中并压紧,再夹持在试验机钳口内进行拉伸试验[16-17]。

选取距钢丝绳固定端分别为80,100,120,140, 160和180 mm距离的6个测试点,分别在轴向载荷20 kN和40 kN工况下拉伸试验。将右交互捻钢丝绳仿真模拟及试验结果和右同向捻钢丝绳仿真模拟结果进行对比分析,结果如图10所示。

图10 钢丝绳模拟仿真与试验结果对比Fig．10 Comparison of the deformations of the ropes obtained by the present finite element analysis with those obtained experimentally

通过模拟仿真与试验数据对比分析,右同向捻与右交互捻钢丝绳仿真模拟值与试验值变化趋势大致相同,最大误差为7%。通过对误差的分析,误差的来源主要有两个:一是模拟仿真时忽略了钢丝之间的摩擦效应,假设钢丝之间润滑良好;二是试验误差主要由仪器误差和读数误差等。

4 结 论

(1)建立了14-6×36WS-IWRC钢丝绳有限元分析模型,仿真模拟计算出股内钢丝应力及变形的分布规律。

(2)右交互捻钢丝绳某一股每层离股芯最近钢丝的等效应力和变形值绕股芯旋转180°即为与该股对称绳股的等效应力和变形值。每股中最大、最小等效应力均分布在靠近钢丝绳芯位置。

(3)右同向捻钢丝绳模型中相邻3股中每股钢丝的变形分布情况和最大、最小等效应力呈现相似情况。相邻股钢丝的等效应力相位差为60°。

(4)钢丝绳股内应力及变形分布规律与钢丝的捻向组合方式相关,同向捻钢丝绳股内应力及变形明显对于交互捻的。因此,交互捻钢丝绳优先选用。

(5)通过模拟仿真计算与钢丝绳拉伸试验对比,在误差允许的范围内,模拟仿真值与试验数据值基本吻合,验证了模型的正确性。

[1] 马 军,葛世荣,张德坤．钢丝绳股内钢丝的载荷分布[J]．机械工程学报,2009,45(11):277-282．

Ma Jun,Ge Shirong,Zhang Dekun．Load distribution on the unit of the wire rope strand[J]．Journal of Mechanical Engineering,2009, 45(11):277-282．

[2] Judge R,Yang Z,Jones S W,et al．Full 3D finite element modelling of spiral strand cables[J]．Constr．Build．Mater,2012,35:452-459．

[3] Nawrocki A,Michel L．A finite element model for simple straight wire rope strands[J]．Comput．Struct．,2000,77:345-359．

[4] Stanova E,Fedorko G,Fabianc M,et al．Computer modelling of wire strands and ropes part II:Finite element-based applications[J]．Adv．Eng．Software,2011,42:322-331．

[5] Jiang W G,Henshall J L,Walton J．A concise finite element model for three-layered[J]．Int．J．Mech．Sci．,2000,42:63-86．

[6] Jiang W G,Warby M K,Henshall J L．Statically indeterminate contacts in axially loaded wire strand[J]．Eur．J．Mech．A．Solids．, 2008,27(1):69-78．

[7] Jiang W G．A concise finite element model for pure bending analysis of simple wire strand[J]．Int．J．Mech．Sci．,2012,54:69-73．

[8] Cengiz Erdonmez,C Erdem Imrak．A finite element model for independent wire rope corewith double helical geometry subjected to axial loads[J]．Indian Academy of Sciences,2011,36(6):995-1008．

[9] Wang D G,Zhang D K,Zhang Z F,et al．Effect of various kinematic parameters of mine hoist on fretting parameters of hoisting rope and a new fretting fatigue test apparatus of steel wires[J]．Eng．Fail．A-nal．,2012,22:92-112．

[10] Wang D G,Zhang D K,Wang S Q,et al．A Finite element analysis of hoisting rope and fretting wear evolution and fatigue life estimation of steel wires[J]．Eng．Fail．Anal．,2013,27:173-193．

[11] Elata D,Eshkenazy R,Weiss M P．The mechanical behavior of a wire rope with an independent wire rope core[J]．International Journal of Solids and Structures,2004,41(5-6):1157-1172．

[12] 孙建芳．钢丝绳捻制成形数值模拟与制品力学强度分析[D]．武汉:华中科技大学,2004:28-29．

Sun Jianfang．Numerical simulation on laying process and strength analysis of metal wire rope[D]．Wuhan:Huazhong University of Science and Technology,2004:28-29．

[13] Feyrer K．Wire ropes,tension,endurance,reliability[M]．Berlin: Springer-Verlag,2007．

[14] 王桂兰,赵瑞敏,孙建芳,等．基于微分几何学的钢丝绳结构CAD[J]．华中科技大学学报,2003,31(6):4-6．

Wang Guilan,Zhao Ruimin,Sun Jianfang,et al．CAD of wire rope structure based on the differential geometry[J]．Journal of Huazhong University of Science and Technology,2003,31(6):4-6．

[15] 刘鸿文．材料力学[M]．北京:高等教育出版社,2004．Liu Hongwen．Mechanics of materials[M]．Beijing:Higher Education Press,2004．

[16] 乌慧霞,郭海森,何 丽．卧式拉力试验机的研制及钢丝绳拉伸试验方法探讨[J]．工程与试验,2011(S1):39-41．

Wu Huixia,Guo Haisen,He Li．Development for horizontal tension testing machine and discussion on steel tightwire tension test method[J]．Engineering&Test．,2011(S1):39-41．

[17] GBT 228—2002,金属材料拉伸试样国家标准．(金属材料室温拉伸试验方法)[S]．

34届国际采矿岩层控制会议通知

国际采矿岩层控制会议(International Conference on Ground Control in Mining,简称ICGCM)由美国工程院院士Syd S．Peng教授创办,自1981年在美国举办以来,至今已成功举办33届。为提升我国在采矿岩层控制领域的研究水平和国际影响力,将在中国举办“34届国际采矿岩层控制会议(中国)”,本次大会将定于2015年10月17—19日在河南理工大学举行。现将有关事项通知如下:

主办单位:河南理工大学、美国西弗吉尼亚大学、中国煤炭学会

协办单位:中国矿业大学、中国矿业大学(北京)、辽宁工程技术大学、太原理工大学、西安科技大学、安徽理工大学、国家自然科学基金委员会、中国煤炭科工集团有限公司、煤炭科学研究总院编辑出版中心、大同煤矿集团有限责任公司、河南能源化工集团有限公司、煤炭安全生产河南省协同创新中心。

1 会议议题

岩层运动与控制,巷道支护技术,煤岩动力灾害及其监测,煤矿开采新技术与装备,资源与环境协调开采,岩层移动与地表沉陷,矿山岩体力学,采矿工程数值分析与仿真,采矿工程实验、测试方法与监测。

2 会议论文投稿说明

(1)会议投稿论文要求为原创、未公开发表的内容,请勿一稿多投;

(2)所有论文只需提交中文版格式,被录用的论文需提交中文版论文全文和2000字左右的中文精简版论文;

(3)录用论文的中文精简版论文将由组委会免费统一翻译成英文,并择优推荐至《International Journal of Coal Science&Technology》《International Journal of Mining Science and Technology》《Journal of Rock Mechanics and Geotechnical Engineering》正刊发表;录用论文中的优秀中文论文择优推荐至《煤炭学报》或《煤炭科学技术》正刊发表;

(4)会议论文将分别出版中文全文论文集和中文精简版英文论文集; (5)投稿电子邮箱:icgcmchina@gmail．com,icgcmchina@163．com。

3 会议论文投稿日期

(1)2015年3月15日前提交200字论文摘要;(2)2015年4月19日发出论文摘要录用通知;(3)2015年6月22日前提交论文全文与精简版论文(2000字);(4)2015年7月22日发出论文录用通知和修改意见;(5) 2015年8月10日前作者提交修改后的全文;(6)2015年10月17日代表报到;(7)2015年10月18—19日学术交流。

4 会议联系方式

联系人:南 华(13569149976)、杜 锋(18037026758)、李振华(15978790618)

电 话(传真):0391-3987946 邮 编:454000

地 址:河南省焦作市高新区世纪大道2001号河南理工大学能源科学与工程学院

Distribution of equivalent stresses and deformations for 6 strand warrington-seale rope with an independent wire rope core

WU Juan1,2,KOU Zi-ming1,2,LIU Yu-hui1,2,WU Guo-xiong1,2
(1.College of Mechanical Engineering,Taiyuan University of Technology,Taiyuan 030024,China;2.Shanxi Provincial Engineering Laboratory(Research Center)for Mine Fluid Control,Taiyuan 030024,China)

The space curve of double helical wire for the right lang lay rope was deduced based on the space curve of single helical wire by Frenet-Serret frame．A realistic three-dimensional modeling approach and finite element analysis of ropes with 14 mm diameter were developed and two cables with different lay directions were modeled．The finite element analyses of two ropes were conducted based on Augmented-Lagrangian algorithm and the corresponding contact parameters．The results show the variation regularity of equivalent stresses and deformations of two ropes．The lay direction and spatial position of double helical wires have a great influence on the equivalent stresses and deformations of wires．In the two ropes,the equivalent stresses of double helical wires are not homogeneous．The double helical wires’stress has a great relationship with the spatial position of wires．The zone of maximum equivalent stresses is the zone of curvature change．The distribution of deformations in the right lang lay rope is analogous to that of the regular lay rope．The distributions of wires’deformations in each layer are sine or cosine distributions．In two ropes,the deformations of wire near to the core strand are larger than that of strand central wire,and the deformations of wires far away from the core strand are smaller than that of strand central wire．The equivalent stresses and deformations of the right lang lay rope are higher than those of the right regular lay rope．The results of present finite element analysis are valid in com-parison with those of experimental data．

independent coire rope core;multi strand construction;distribution of stress and deformation;finite element method

TD532

A

0253-9993(2014)11-2340-08

2013-11-06 责任编辑:许书阁

国家自然科学基金青年科学基金资助项目(51205272);国家国际科技合作专项资助项目(2011DFA72120)

吴 娟(1977—),女,重庆万州人,副教授,博士。E-mail:wujuanz@163．com。通讯作者:寇子明(1964—),男,陕西吴堡人,教授,博士生导师。E-mail:zmkou@163．com

吴 娟,寇子明,刘玉辉,等．独立钢丝绳芯钢丝绳应力及变形分布[J]．煤炭学报,2014,39(11):2340-2347．

10．13225/j．cnki．jccs．2013．1629

Wu Juan,Kou Ziming,Liu Yuhui,et al．Distribution of equivalent stresses and deformations for 6 strand warrington-seale rope with an independent wire rope core[J]．Journal of China Coal Society,2014,39(11):2340-2347．doi:10．13225/j．cnki．jccs．2013．1629