直驱式回转工作台传动性能分析

袁胜万，余正斌，聂艳，余颖

(沈机集团昆明机床股份有限公司，云南昆明 650203)

振动、噪声、传动精度及运动稳定性是研究转台传动系统重点关注的问题，国内外学者针对这些问题已经做了大量工作［1］。哈尔滨工业大学的谢涛［2］采用有限元方法对飞行转台进行结构动力学分析和优化设计，并获得良好的应用;美国J G BLANCHE等［3］使用纯几何学的方法研究了摆线针轮减速机构的传动精度;前苏联勃鲁也维奇［4］提出使用概率统计法对机构的传动精度进行计算，对机构精确度线性理论、机构精确度的计算、概率模拟的应用、随机变量典型分布规律等进行了系统的论述，受到业界的肯定与推崇;日本日高照晃等［5］应用“等价模型”的方法对2K-V型摆线针轮传动机构的传动精度进行了研究，将机构转化为相应的等价模型，建立了摆线针轮行星传动误差的数学模型，并讨论了各个零部件的装配误差、加工误差以及间隙等对传动精度的影响。

文中的研究对象为直驱式精密回转工作台传动系统，采用力矩电机直接驱动回转工作台传动，其传动结构简单，基于集中参数法及等价误差法分别建立转台传动系统动力学模型和传动精度模型，对该传动系统动态响应特性和传动精度进行分析，研究和改善影响转台传动系统性能和精度的因素，以提高传动系统的承载能力、动态性能及传动精度，为工程实践中传动系统性能提升提供理论参考。

1 精密回转工作台传动系统动力学建模

1.1 精密转台传动系统传动示意图

由于对精密转台性能要求的不断提高，为了满足精密转台的传动精度及快速响应要求，针对某厂研制的TGK46100高精度坐标镗床 (其回转速度要求10 r/min，定位精度要求3″)，转台传动系统采用力矩电机直接驱动。传动系统如图1所示。

图1 回转工作台传动系统图

1.2 精密转台传动系统动力学方程

根据集中参数法建立实际转台传动系统动力学模型［6］，传动系统动力学模型如图2所示，其动力学方程如式 (1)所示:

其中:Ts、Tc分别为电机扭矩、切削负载阻力矩;Is、Ig分别为电机轴的转动惯量、负载的转动惯量;θs、θg分别为电机转子的扭转角、输出轴的扭转角;cs、ks分别为电机轴与工作台连接件的扭转阻尼、扭转刚度。

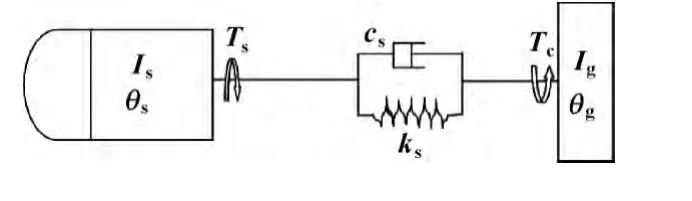
图2 回转工作台动力学模型

1.3 传动系统激励分析

回转工作台是由力矩电机直接驱动的，因此作者主要研究电机与工作台连接件的扭转刚度和阻尼。

(1)连接轴的扭转刚度

按照材料力学的方法，可以计算出传动轴的扭转刚度:

式中:G为齿轮轴的切变模量;l为两齿轮所在轴段的长度;Iz为轴段截面极惯性矩。

(2)连接轴的扭转阻尼

分析系统工作过程主程序在上电后需要立即被执行，完成系统的初始化，对数据存储器、定时器等进行清零。同时对输入、输出端口进行设定来确保接受信号。完成系统初始化后即可利用中断程序，合理调用各个功能子程序，电饭煲系统主程序逻辑设计，如图8所示。

传动轴的扭转振动阻尼主要是材料阻力，根据H H LIN和C LEE等的分析，传动轴的扭转阻尼可表示为:

式中:ki为轴的扭转刚度;I1、I2分别是轴上两质量块的转动惯量;ξ为阻尼比，根据D R Houser等的试验研究，ξ一般取值范围为0.005～0.075。

(3)外部激励

振动系统在随时间变化的外力作用下所产生的运动，一般称为系统对该外力的响应，此外力称为激振力。激振的形式很多，按它们随时间变化的规律划分则有4种:简谐激振、非谐周期激振、随时间任意变化的非周期性激振和随机激振。激振形式不同，不仅系统的响应不同，分析方法也有一些变化。

一般来说，机器的旋转零部件由于某种原因而不平衡，当它转动时将产生不平衡的离心惯性力，这种力就是典型的简谐激振力［7］。此种简谐激振力可表示为

式中:T为扭矩常量;ω为回转角速度。

2 转台系统动态响应仿真分析及讨论

针对方程 (1)来研究转台系统的动态响应特性，该传动系统的主要参数为ms=26.9 kg;mg=890 kg，Is=1.19 kg·m2;Ig=40.05 kg·m2;Rs=0.212 m;Rg=0.3 m;ks=1.06×109N/m;cs=50。

回转工作台的动力学方程为时变型非线性微分方程，若用解析法求解将是很困难的，而且很难求得精确解。因此，文中采用5阶变步长自适应Newmark-β解法进行求解［8］，获得传动系统中输入、输出部件的动态响应。时域响应取1.0 s的响应进行分析。经过计算可以得到回转工作台输入、输出轴的扭转振动速度以及加速度值，如图3—4所示。

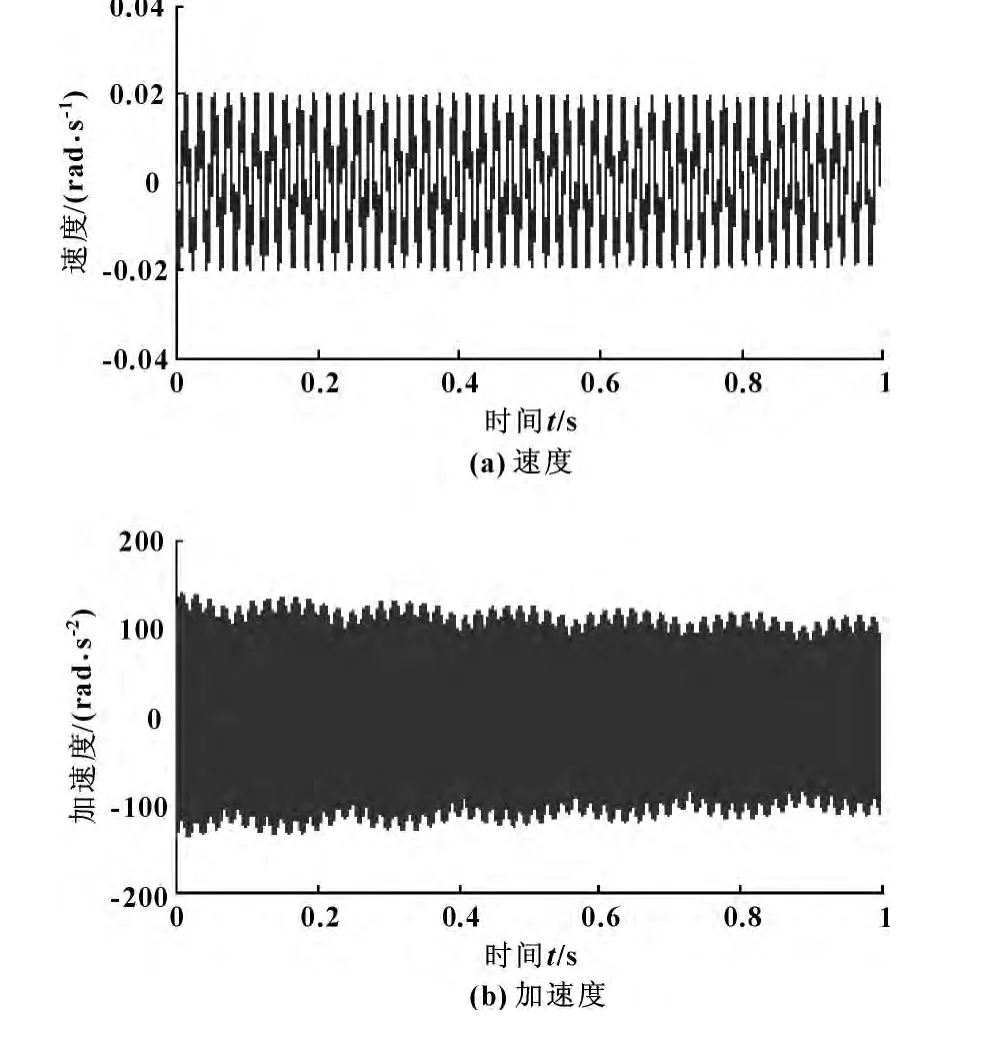
图3 输入轴振动速度及加速度值

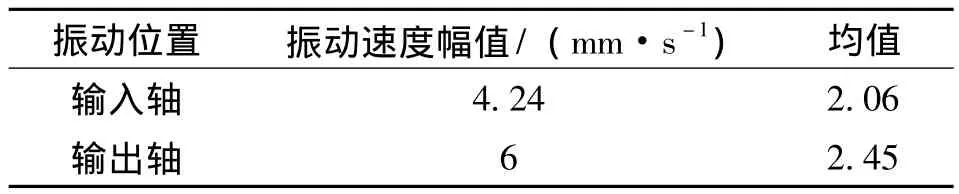
表1 输入输出轴振动速度均值

按照GB/T6404.2《齿轮装置的验收规范》对回转工作台的振动进行评价，输入轴的振动速度均值为2.06，在振动评价曲线中位于A级水平;输出轴的振动速度均值为2.45，同样在振动评价曲线中处于A级水平，表明输入轴与输出轴在高速输入情况下振动情况均为良好。传动系统可以获得很高的动态响应性能。

3 回转传动精度建模及误差分析

回转传动误差是指:对应着同一输入回转角，输出轴的实际回转角与理论回转角之间的差值［9］。若令电机轴的输入角为θ1，工作台的实际回转角与理论回转角分别为θ'2和θ2，则直驱式回转工作台回转传动误差为:

采用等价误差法对精密回转工作台的传动系统进行回转精度建模［9］。工作台的回转传动系统同图1所示，根据传动结构建立传动精度模型，其传动精度模型在图2基础上考虑加速度及等价误差产生附加力矩影响。

综合考虑转台各传动零件的等价误差，以及运动的加速度，利用牛顿第二定理进行传动精度数学模型的建立。

3.1 回转传动系统的误差分析

(1)滚动轴承动环偏心

如图5所示，设轴承内环与齿轮孔的径向跳动公差为δu，则旋转偏心为e=1/2δu。则旋转偏心引起的圆周方向上的等价误差eu为:

式中:θ=ωt，为轴承旋转的角度值;ω为轴承旋转的角速度。

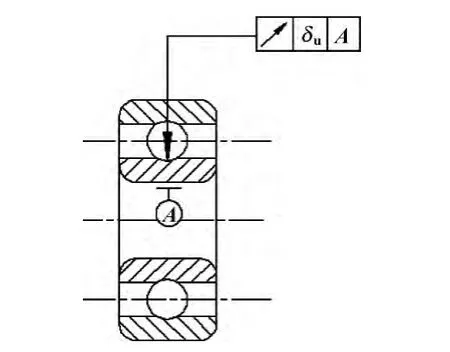
图5 滚动轴承动环偏心

(2)轴承径向游隙

设径向游隙的最大值为Δrmax，最小值为Δrmin，且径向游隙Δr引起的角位移等价误差er为:

式中:R为轴承的旋转半径。

(3)轴承内环与轴的间隙

轴承内环与轴的间隙ΔCbi和轴承径向游隙的分布相同，其引起的角位移等价误差ebi为:

式中:R为轴承的旋转半径。

3.2 传动精度数学模型的建立

根据上述各个零件的等价误差及其回转工作台的数学模型，考虑零件运动的加速度，利用牛顿第二定理得到下列的平衡方程式［10-11］:

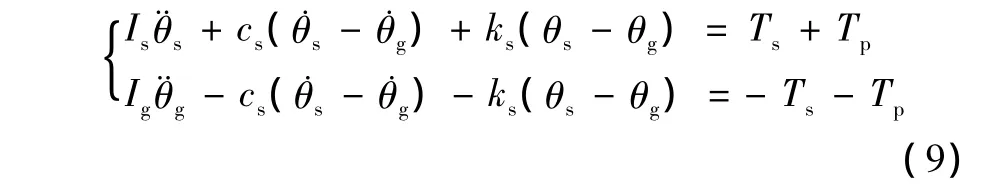
式中:Tp为等价误差产生的附加力矩，其余同式(1)相 同;Tp=kse+cs，e=e0+eusinωt，e0=

3.3 回转工作台回转传动精度的求解

根据传动系统误差分析，确定其轴承的误差参数如下:滚动轴承动环偏心δu=7.5 μm，径向游隙Δr=11 μm，轴承内环与轴的间隙ΔCbi=4 μm。根据Newmark-β法对传动精度方程进行求解，从而得到回转工作台回转传动系统的传动精度。输出轴的回转传动误差如图6所示。

图6 输出轴的回转传动误差

图6中的结果即为输出轴的误差弧度值，当工作台运转稳定后对其传动误差进行分析可知，其传动误差幅值为1.4×10-5rad，转换成角度值为2.68″;相邻两个周期的误差幅值的差值约为0.6×10-6rad，对其进行角度转换可得0.12″。

工作台回转定位精度的验收条件:要求定位精度达到3″，重复定位精度达到2″。二者进行对比可知，计算得到的结果中定位精度与重复定位精度均满足验收条件。因为工作台采用力矩电机直驱式，传动链较短，回转B坐标采用高刚度、高精度轴向径向转台轴承实现工作台机构轴向、径向精确定位，配合高精度的圆光栅作为检测元件，从而提高工作台的高回转精度及定位精度。

在此种情况下，若想进一步提高工作台的回转传动精度，一是提高力矩电机与工作台连接件的扭转刚度，减小其变形，从而减小传动误差;二是选择精度等级比较高的转台轴承，减小轴承间隙及其偏心，从而减小传动误差;三是通过伺服控制系统进行调节，提高定位精度［12］。

4 结论

建立了一种直驱式回转工作台动力学模型和传动精度模型，系统地研究了精密转台在自激作用下的动态响应和传动精度及其影响因素，其结论如下:

(1)利用Newmark-β数值方法求解得出了弧齿锥齿轮传动系统的动态响应，分析表明:传动系统在高速输入情况下振动情况良好，传动系统可以获得很高的动态响应性能。

(2)针对影响机构传动精度的各零件的加工误差和装配误差等因素进行建模分析，理论分析发现重复定位精度与定位精度均满足验收条件。通过与实际测试结果对比发现:由于理论分析忽略了其他一些诸如轴承等的制造和安装误差对传动精度的影响因素，其分析结果与测试结果有一定差距，需要对转台进行消隙处理，以进一步提高其传动精度。

［1］CHENG Y，LIM T C.Vibration Analysis of Hypoid Transmissions Applying an Exact Geometry-based Gear Mesh Theory［J］.Journal of Sound and Vibration，2001，240(3):519-543.

［2］谢涛.飞行仿真转台结构动力学分析及其优化设计研究［D］.哈尔滨:哈尔滨工业大学，2003.

［3］BLANCHE J G，YANG D C H.Cyeloid Drives with Machining Tolerances［J］.Journal of Mechanisms，Transmisslons，and Antomation in Design，1989，111(9):337-344.

［4］勃鲁也维奇.机构精确度［M］.上海:上海技术出版社，1964.

［5］日高照晃，王宏猷，石田武.采用摆线齿轮的K-H-V行星齿轮装置回转传动误差的研究［C］//日本机械学会论文集(C编)，1994:281-289.

［6］刘光磊，沈允文，王三民.动态计入轮齿啮合力的弧齿锥齿轮转子系统振动模型［J］.机械科学与技术，1998，17(S1):67-69.

［7］姚文席，魏任之.渐开线直齿轮的啮合冲击研究［J］.振动与冲击，1990，36(4):57-61，25.

［8］冯领香，魏建国，王森林，等.一种可自调步长的改进Newmark 算法［J］.河北农业大学学报，2004，27(3):111-114.

［9］李军，李润方，林超，等.小模数精密齿轮传动误差分析及实验研究［J］.机械，2003，30(7):15-17.

［10］韩林山，谭群燕，沈允文，等.间隙及转矩对2K-V型传动装置传动精度的影响［J］.机械科学与技术，2007(8):1080-1089.

［11］李伟，李力行，叶庆泰.基于概率理论的RV减速器的传动误差计算［J］.机床与液压，2004(1):122-123.

［12］中国振动联盟.http://www.chinavib.com/.