非合作航天器相对姿态确定算法及地面试验

翟 坤，曲 溪，李 志，陈新龙

(1.清华大学航天航空学院，100084 北京;2.中国空间技术研究院载人航天总体部，100094 北京;3.中国空间技术研究院钱学森空间技术实验室，100094 北京)

非合作航天器相对姿态确定算法及地面试验

翟 坤1，曲 溪2，李 志3，陈新龙3

(1.清华大学航天航空学院，100084 北京;2.中国空间技术研究院载人航天总体部，100094 北京;3.中国空间技术研究院钱学森空间技术实验室，100094 北京)

针对具有矩形结构的非合作航天器，采用坐标转换矩阵的姿态描述方法，推导了简单通用的单目视觉相对姿态确定算法.为验证相对姿态确定算法，基于MATLAB设计图像采集处理系统，采用STK设计目标模拟器，进而搭建了地面试验系统，并开展了非合作航天器轨道面内和轨道面外绕飞试验.试验结果表明相对姿态确定算法能够准确地获得非合作航天器的相对姿态变化.

非合作航天器;单目视觉;相对姿态确定;目标模拟器;地面试验

非合作航天器间相对位姿测量是进行绕飞监测和交会对接等在轨操作的前提［1－2］.最常用的相对位姿测量方法是基于视觉的测量方法.非合作航天器相对位姿视觉测量的研究很多［3－7］，哈工大的张世杰等［4－5］研究了利用单目视觉进行非合作航天器相对位姿参数的确定问题，提出了Levenberg-Marquardt最优化方法的迭代算法，但该算法是假设被识别目标的几何尺寸为已知.文献［6］提出了相对姿态正交迭代算法，将目标空间最小共线性误差作为目标函数，采用迭代求解方法同时得到旋转矩阵和平移矩阵，该算法假设被识别目标特征点的空间坐标已知.北京控制工程研究所的张劲锋等［7］采用类似的正交迭代算法，提出一种深度迭代算法，通过引入深度变量，将2D－3D问题转化为迭代求解3D－3D问题，但同样假设被识别目标特征点的空间坐标已知.

上述方法都假设目标尺寸为事先已知，在实际应用中具有一定的局限性.针对航天器一般都有矩形结构，如立方体的主体结构、方形的太阳帆板等，合肥工业大学的高学海等［8］采用单目摄像机和激光测距仪，以航天器某矩形面为观测目标，提出了尺寸未知的航天器相对位姿测量方法，该方法是对Haralick提出的空间尺寸未知矩形姿态测量算法［9－10］的进一步改进.

由于相对位置通常根据激光测距仪的测量信息得到，而地面较难模拟实际的航天间相对位置及激光测距仪的测量过程，所以本文只进行航天器间相对姿态确定算法及地面试验的研究.

文献［8］仅针对坐标转换顺序Z→X→Y推导得到的相对姿态，算法具有一定的局限性，如果换成其他坐标转换顺序，必须进行重新推导，且推导过程较复杂.本文基于坐标转换矩阵，首先给出了一种简单通过的单目视觉相对姿态推导方法，然后设计地面试验系统，并通过试验分析验证相对姿态测量算法.

1 相对姿态确定算法

相对姿态是指目标航天器相对追踪航天器的姿态，由于视觉相机在追踪航天器上的安装姿态已知，所以通常研究中把目标航天器相对视觉相机的姿态定义为相对姿态.

假设航天器主体结构为立方体，以立方体的一个面作为观测目标，说明相对姿态测量算法.相机和目标关系定义如图1所示.

图1 相机与目标的坐标关系

图1中共定义了3个坐标系:

1)像平面坐标系ouv——原点o在成像平面的中心，ou轴和ov轴分别沿着像平面的横轴和纵轴方向;

2)相机坐标系OcXcYcZc——原点Oc位于相机镜头的中心，OcYc和OcZc轴分别平行于成像平面的ou轴和ov轴，轴与相机光轴重合，指向相反.原点Oc到像平面的距离为f(即相机焦距);

3)目标坐标系OtXtYtZt——原点Ot位于目标航天器质心，OtXt、OtYt和OtZt轴分别平行于航天器主惯量方向.

图1 中 Pi(i=1，2，3，4)为被观测矩形面(也称感兴趣矩形面，简称ROI)的4个顶点，可得4个顶点在OtXtYtZt和OcXcYcZc中的表示有如下关系:

由目标坐标系的定义可知，点Pi(i=1，2，3，4)在目标坐标系可表示为

其中:x1t=H/2，y1t=-L/2，z1t=-W/2，H、L和W分别为目标航天器边长.

而由相机成像原理可得

其中:f是相机的焦距，ui和vi分别为点Pi在像平面投影点的坐标，通过对相机拍摄的图像进行处理可以求得.

将式(2)和式(3)代入式(1)，并化简可得

式(4)+式(5)－式(6)得

整理可得

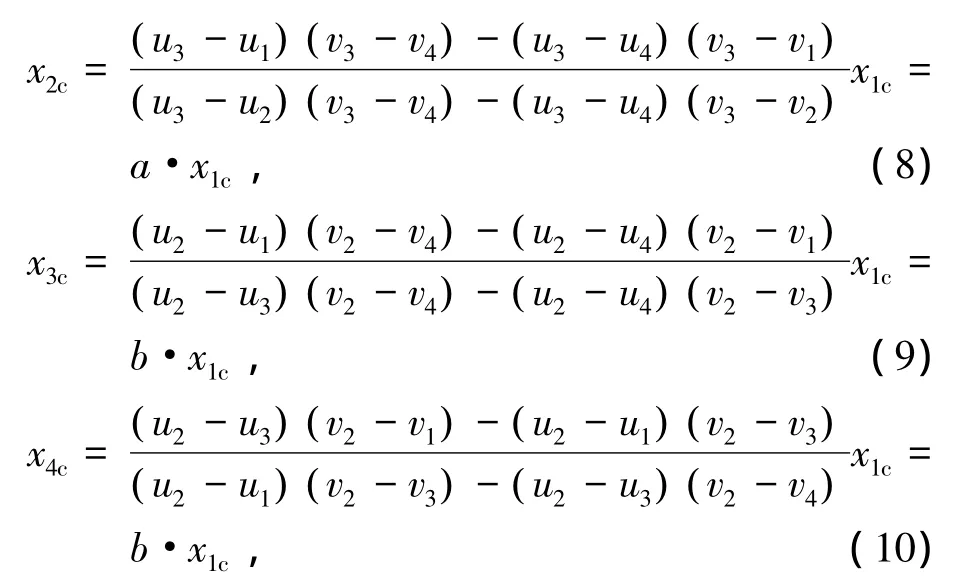
将式(8)代入式(4)，式(9)代入式(5)，可得

取坐标转换矩阵 Rct=［r1r2r3］，r1、r2和r3是三维列向量，且‖r1‖=‖r2‖=‖r3‖=1，则由式(11)和式(12)可得

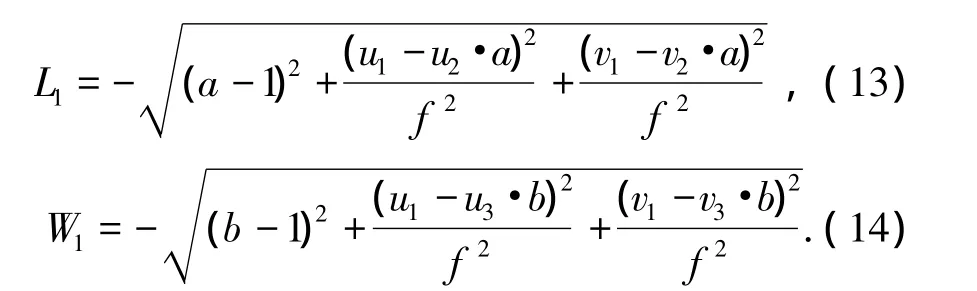
因为图1中定义相机坐标系的轴为目标的反方向，即x1c为负数，所以式(13)和式(14)中的L1和W1均为负数.

将式(13)代入式(11)，式(14)代入式(12)，

可得

由式(15)、式(16)和式(17)可知，只要知道感兴趣矩形面的4个顶点Pi(i=1，2，3，4)在像平面投影点的坐标ui和vi，就可以计算得到相对姿态Rct，而无需目标的尺寸.

相对文献［8-9］，本文给出的是坐标转换矩阵表示的相对姿态，没有限定坐标转换顺序，更加通用，同时推导过程非常简洁明了.而求解欧拉角表示的相对姿态，可采用常用的坐标转换矩阵和欧拉角的变换方法.

如果假设由OtXtYtZt到OcXcYcZc的坐标转换顺序为Z→Y→X，并将坐标转换矩阵Rct写成分量形式有

式中Rct(1，1)是Rct的第1行，第1列的分量，其他同.

则可得:

1)当 |Rct(1，3)|=1时，

2)当 |Rct(1，3)|＜ 1时，

词大体上也可以说是南方文学，早期的词作者主要是以浙江、江西、江苏、福建为代表的南方人，词中的景象与人物也多是江南的小桥流水、杨柳依依、莲娃歌女等。

2 地面试验系统

为了有效地验证相对姿态确定算法，搭建如图2所示的地面试验系统.整个试验系统包括视觉采集相机、固定调整机构、图像采集处理计算机和目标航天器模型(简称目标模拟器).

图2 地面试验系统组成示意图

2.1 视觉采集相机

视觉采集相机用于获得目标航天器图像，并输出给图像采集处理计算机.采用德国AVT的Guppy PRO F－125B工业相机，该相机焦距为8 mm，分辨率为1 292×964.

2.2 固定调整机构

固定调整机构用于安装固定相机和目标模拟器，为相机提供4个自由度(相机前进方向的平动、升降平动、除垂直的两个方向转动)，用于调整相机和目标模拟器的初始对准情况.

2.3 图像采集处理计算机

图像采集处理计算机采用普通PC机，通过1394接口与视觉采集相机通信，获得相机的输出.

本试验系统基于MATLAB/Simulink的图像处理功能完成图像采集处理程序的开发.图像采集处理程序分为图像采集、图像处理和相对姿态计算3个部分，具体处理流程如图3所示.

图3 图像处理流程

图像采集部分采用 Simulink/Image Acquistion Toolbox/From Video Device模块，获得视觉采集相机的输出.

图像处理部分采用Simulink/Video and Image Processing Blockset里面的若干模块，对采集的输出进行边缘检测、Hough变换等操作，最后得到感兴趣矩形面4个顶点的像点坐标.

相对姿态计算部分是基于第1节的算法搭建而成的.

2.4 目标模拟器

目标模拟器采用1台PC机实现，该PC机的显示屏固定于基准平台上(如图2所示)，PC机内运行目标航天器模拟程序，生成试验系统的目标航天器模型.

假设目标航天器是边长为3 m的中心刚体，并带有两个长10 m、宽3 m的太阳翼，运行于距相机100 m的位置.

首先采用Modeler以实际尺寸设计目标航天器的模型，如图4所示.

图4 目标航天器模型

为保证目标显示屏能够完整显示目标模拟器，设置3D Attitude Graphics显示窗口的视场角为30°(半视场角为15°)，则

即目标显示屏可显示距相机100 m处半径为53.59 m的圆形范围，能够显示目标航天器的完整模型.

令d为目标模拟器距相机的距离，则

其中:SH是显示屏水平分辨率，r为显示屏的点距.

如果目标模拟器选用17 in的显示器，水平分辨率 为1 280，点 距 为 0.264 mm，则 d=615.79 mm，即目标显示屏应放置在距相机615.79 mm的位置，才能保证相机观测目标模拟器所确定的相对姿态与观测100 m处的实际目标的相对姿态一致.

3 验证试验

基于地面试验系统，通过两种工况验证改进的相对姿态确定算法.

工况1:目标模拟器绕Y轴匀速转动，模拟追踪航天器(相机)相对目标航天器在轨道面内的绕飞过程.设定目标航天器相对姿态角变化规律为

工况2:目标模拟器绕Z轴匀速转动，模拟追踪航天器(相机)相对目标航天器在轨道面外的绕飞过程.设定目标航天器相对姿态角变化规律为

试验结果如图5、6所示，分别表示两种工况下相对姿态确定算法的计算结果与设定姿态角的偏差.对两种工况的跟踪偏差结果进行统计可得:工况1的俯仰角跟踪偏差均值为0.23，最大偏差达到2.6°.工况 2的偏航角跟踪偏差均值为0.05°，最大偏差达到 3°.

图5 工况1的俯仰角跟踪偏差曲线

图6 工况2的偏航角跟踪偏差曲线

由统计结果可知，相对姿态的跟踪偏差均值较小，但存在较大的振荡变化，可通过滤波处理提高相对姿态的精度.

4 结语

本文研究了具有矩形特征的非合作航天器的单目视觉姿态确定算法，并进行了地面试验分析.相对以往的相对姿态确定算法，本文推导的算法更加通用，推导过程简单.应用地面试验系统开展了两种工况的相对姿态确定算法验证，试验结果表明确定的相对姿态存在较大的振动偏差和较小的均值偏差，可通过滤波处理得到更高精度的结果.试验系统可进一步改造用于非合作航天器在轨操作等任务的地面试验.

［1］崔乃刚，王平，郭继峰，等.空间在轨服务技术发展概述［J］.宇航学报，2007，28(4):805－811.

［2］梁斌，杜晓东，李成，等.空间机器人非合作航天器在轨服务研究进展［J］.机器人，2012，34(2):242－256.

［3］徐文福，刘宇，梁斌，等.非合作航天器的相对位姿测量［J］.光学精密工程，2009，17(7):1570－1581.

［4］张世杰，曹喜滨，陈闽.非合作航天器间相对位姿的单目视觉确定算法［J］.南京理工大学学报，2006，30(5):564－568.

［5］张世杰，谭校纳，曹喜滨.非合作航天器相对位姿的鲁棒视觉确定算法［J］.哈尔滨工业大学学报，2009，41(7):6－10.

［6］LU C P，HAGER G，ERIC M.Fast and globally convergent pose estimation from video images ［J］.IEEE Transactions on PAMI，2000，22(6):610－622.

［7］张劲锋，孙承启，蔡伟.基于单目视觉的非合作航天器相对位置和姿态测量算法［J］.空间控制技术与应用，2009，35(6):50－53.

［8］高学海，徐科军，张瀚，等.基于单目视觉和激光测距仪的位姿测量算法［J］.仪器仪表学报，2007，28(8):1479－1485.

［9］HARALICK R M.Determining camera parameters from the perspective projection of a rectangle［J］.Pattern Recognition，1989，22(3):225－230.

［10］PENNA M A.Determining camera parameters from the perspective projection of a quadrilateral［J］.Pattern Recognition，1991，24(6):225－230.

Ground test and relative attitude determination algorithms of non-cooperative spacecraft

ZHAI Kun1，QU Xi2，LI Zhi3，CHEN Xinlong3

(1.School of Astronautics and Aerospace，Tsinghua University，100084 Beijing，China;2.Institute of Manned Space System Engineering，China Academy of Space Technology，100094 Beijing，China;3.Qian Xuesen Laboratory of Space Technology，China Academy of Space Technology，100094 Beijing，China)

Aiming at non-cooperative spacecraft with rectangular structures，a more simple and general relative attitude determination algorithm was deduced by expressing the relative attitude in the form of coordination transformation matrix.To verify the method，the image acquisition and processing system was designed based on MATLAB，and using STK the target simulator was built.Furthermore a ground test system was established，and the tests of flying around in the orbit plane and out of the orbit plane were performed.The results indicate that the relative attitude determination algorithm can derive the relative attitude of non-cooperative spacecraft exactly.

non-cooperative spacecraft;monocular vision;relative attitude determination;target simulator;ground test

V448;TP391.41

A

0367－6234(2014)03－0061－05

2013－03－26.

国家高技术研究发展计划资助项目(2012AA7096017).

翟 坤(1979—)男，讲师;

李 志(1966—)男，研究员，博士生导师.

翟 坤，zhaikun@tsinghua.edu.cn.

(编辑 张 宏)