砂泥岩地层地应力纵向分布特征与规律

张东涛，童亨茂，赵海涛，吕 雪，张 昊

砂泥岩地层地应力纵向分布特征与规律

张东涛1，2，童亨茂2，赵海涛3，吕 雪1，张 昊1

（1.中国石油大学（北京）油气资源与探测国家重点实验室，北京102249；2.中国石油天然气股份有限公司浙江油田分公司，杭州310023；3.天津城建大学地质与测绘学院，天津300384）

以实际沉积地层中抽象出来的砂泥岩地层概念模型为研究对象，在盆地构造力学、岩石力学性质分析的基础上，采用应力场数值模拟法研究分析砂泥岩地层中的纵向地应力分布特征和规律。研究结果表明，水平主应力在砂泥岩的分界面发生突变，变化程度主要与两侧岩石的力学性质差异相关，也与区域构造应力有一定关联；杨氏模量对最大水平主应力影响程度大于对最小水平主应力的影响，泊松比对地层最小水平主应力影响程度大于对最大水平主应力的影响。杨氏模量和泊松比对最大水平主应力的影响，在伸展应力状态下前者影响相对较小，走滑应力状态下，影响程度基本相同，挤压应力状态下，前者影响程度相对较大；而对于最小水平主应力的影响，在三种应力状态下，泊松比的影响均大于杨氏模量。地层的岩性变化方式（渐变或突变）对地层最小水平应力差产生显著影响，厚度变化对地层最小水平应力差大小无影响。上述认识可以指导砂泥岩地层的压裂和储层改造，改善压裂效果。

地应力分布；数值模拟；泊松比；杨氏模量；砂泥岩

0 引言

随着地下深部矿产资源（如油气、页岩气、煤等）的勘探开发，地应力分布特征与规律的研究日益受到重视。有国外学者统计了世界不同地区地应力的测量结果，总结了垂直应力、水平平均主应力与垂直应力之比随埋深的分布规律［1～4］。国内学者则在统计我国不同地区地应力测量结果的基础上，总结了最大、最小水平应力和垂直应力在一定深度区间内与深度的关系［5～9］。秦向辉等［10］统计了实测地应力与杨氏模量的关系，发现水平最大主应力和水平最小主应力与杨氏模量成正相关。景锋等［11］统计分析认为地应力随泊松比的增大而减小。Gudmundsson［12～14］指出水平地应力对岩石的杨氏模量很敏感。总的来说，已有的研究侧重地应力的测量、区域地应力的分布特征和规律研究，相对比较宏观，而对于地质体内部（如砂泥岩间互地层）地应力的精细分布特征和规律的研究则较缺乏。

随着油气勘探开发的不断深入，油气勘探开发的难度不断加大，需要进行地层压裂和改造的储层（如低渗透储层）比例不断加大。目前中国探明的石油地质储量中，低渗透储量所占的比例高达60%～70%［15］，低渗透层将是我国今后相当长时期增储上产的主要基础资源。低孔渗油藏的开采及增产需要进行储层改造，现今低孔渗储层的改造方式主要是水力压裂，宏观的地应力分布规律已不能满足储层压裂对地应力研究的要求。能否确定油藏地应力的精细分布是决定储层压裂成败的关键因素，而这方面还缺少深入研究。

在地层压裂、储层改造过程中，一方面要实现对砂岩储层的压裂，另一方面，还要把压裂缝控制在砂岩储层内，保证泥岩隔层不被压裂。确定砂泥岩间互地层地应力的分布特征和规律是基础，是实现储层有效压裂的关键。地应力的精细研究不仅是储层压裂改造的基础性工作，而且在压裂改造过程中造成断层的再活动分析预测也有重要意义［16～17］。

不同岩性地应力分布的差异本质上是其岩石力学性质（如杨氏模量、泊松比等）的差异引起的。本文针对上述问题，在前人对地应力宏观分布规律研究的基础上，以岩石力学参数变化的剖面地层概念模型为对象，应用ANSYS软件，定量分析岩石力学参数（杨氏模量、泊松比）对地层水平主应力分布的影响以及岩性变化、层厚变化对应力差的影响，确定砂泥岩间互地层地应力的分布特征和规律。

1 砂泥岩地层应力场数值模拟

砂岩和泥岩的力学性质存在显著差异，这是造成砂、泥岩内部地应力分布差异的内因。在地层温压条件下，泥岩一般具有流变特征，表现为泊松比相对较大。岩石力学实验的统计结果表明，泥岩的杨氏模量往往也比砂岩大，但岩性与杨氏模量大小并不是一一对应关系。因此，可以采用不同力学性质的材料模拟地层剖面力学参数变化对地应力分布的影响。

本文采用应力场数值模拟法，利用不同力学参数的材料，模拟分析力学参数变化时剖面地层地应力分布特征和规律。依据有限单元理论，利用应力场数字模拟软件，通过调节泊松比、杨氏模量、地层厚度、缩短量等参数，定量分析不同岩石力学参数对地层地应力分布的影响，模拟确定不同岩石力学参数组合、不同厚度条件下地层地应力分布特征和规律。

1.1 数学模型

模拟采用有限元数学模型，其基本思想可以归结为3个方面：①有限单元离散化；②单元分析；③总体分析。对于平面线弹性问题［18］，用结点位移表示单元内的位移，将结点位移作为基本未知量，建立位移模式。单元内位移｛f｝与结点位移｛δ｝e通过矩阵［N］联系起来的关系式如下：

通过几何方程及本构方程，将单元内应变｛ε｝与应力｛σ｝用结点位移来表示：

式中：［B］和［S］分别为应变和应力矩阵。

将作用在单元上的分布力转化为等效结点力，然后求得单元等效结点力与结点位移分量之间的关系，建立单元的刚度矩阵为：

式中：｛Fi｝为等效结点力；［K］e为单元刚度矩阵。

按最小势能原理，根据单元刚度矩阵，建立总体刚度矩阵：

式中：［K］为总体刚度矩阵，｛R｝为整体介质所有结点的等效结点载荷。

式（6）为有限单元的基本方程，最后归结为解（6）式的方程组，将各单元结点位移｛δ｝e求得后，代入（2）、（3）式，求出各单元应变及应力分量，最终计算出主应力及主方向。

1.2 地质概念模型和力学参数

地质概念模型根据实际地质体（以东海西湖凹陷为背景）建立。模型中力学参数根据东海西湖凹陷有关井的岩石力学试验测试结果和测井解释有关井的岩石力学参数选取；通过区域构造分析、水力压裂测试确定不同地应力状态（伸展、走滑、挤压），以此为基础设定边界条件（包括边界作用方式和作用力大小）。模型虽然以实际地区为背景，但由于砂泥岩地层分布的相似性（砂岩和泥岩间互），本文设计的3类模型，研究成果应该具有广泛的意义。

模型Ⅰ由11层不同岩石力学参数的地层构成（见图1），岩层顶部埋深2000 m，岩层长度100 m，每层厚度均为10 m。调节泊松比、杨氏模量2个参数大小，共建2组（模型Ⅰa、Ⅰb），模拟研究在不同地应力状态下，泊松比、杨氏模量变化对地应力分布的控制和影响。模型Ⅰa、Ⅰb的具体岩石力学参数见表1。

图1 模型Ⅰ网格剖分加载Fig.1 Numerical modelⅠwith boundary conditions

模型Ⅱ由3个砂泥岩沉积的正旋回构成，并根据厚度组合的变化方式划分为3组，模拟研究不同岩石力学参数组合、不同厚度条件下地层地应力分布特征和规律，具体数值模拟岩石力学参数见表2。岩层埋深3000 m，岩层长度100 m，每个旋回的厚度为25 m。3组模型的相同之处是：模型顶底界面海拔深度相同，旋回界面分界线的海拔深度相同，砂泥岩密度

相同，边界构造作用力相同。不同之处是：模型Ⅱa由砂岩突变到泥岩（见图2a）；模型Ⅱb中每个旋回由砂岩渐变过渡到泥岩，其中过渡带地层是等厚的（见图2b）；模型Ⅱc中每个旋回由砂岩渐变过渡到泥岩，其中过渡带地层不等厚（见图2c）。

表1 模型Ⅰa、Ⅰb岩石力学参数分布Table1 Parameters of rock mechanics for modelⅠa andⅠb

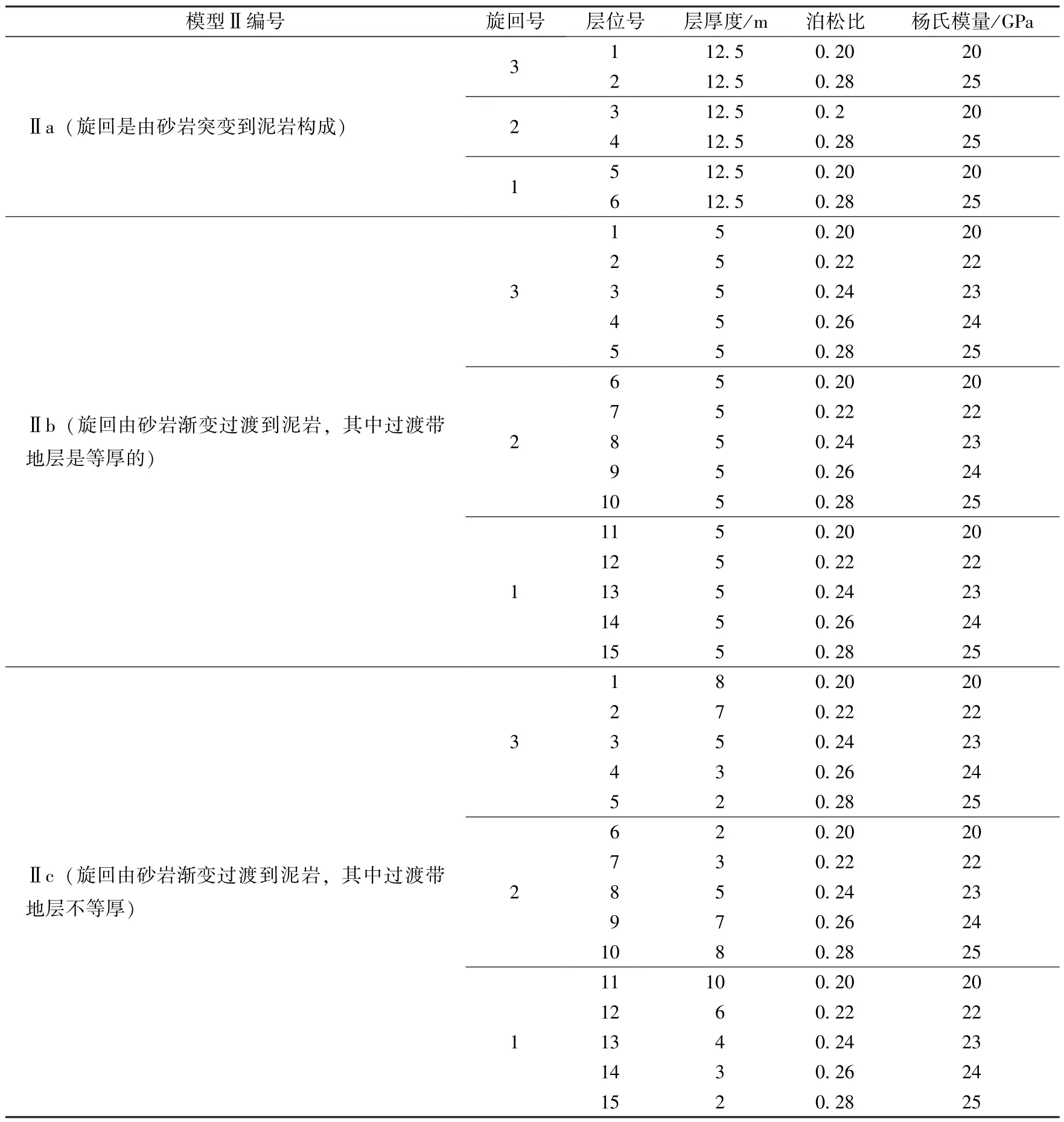
表2 模型Ⅱ岩石力学参数分布Table2 Parameters of rock mechanics for modelⅡ

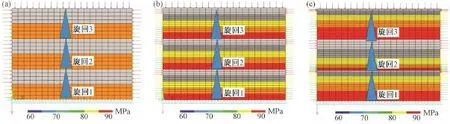
图2 模型Ⅱ网格剖分加载Fig.2 Numerical modelⅡwith boundary conditions

1.3 力学模型

考虑到模型主要应用于地层压裂，而在压裂（短暂变形）过程中浅部地层（小于8 km）一般表现弹性变形的特征，剖面上符合平面应变的规律，为此模型选用平面应变问题的弹性静力学模型。模型顶部加相当于上覆地层重量的载荷，模拟上覆地层的重力作用；侧向加位移载荷（模型Ⅰ），模拟上下地层的统一变形，或梯形载荷（模型Ⅱ），模拟构造作用力和水平重力应力分量叠加产生的作用。二维弹性静力学模型由平衡方程、几何方程、本构方程和边界条件组成［19～20］。

1.4 网格剖分、约束条件和边界力作用方式

两类模型的网格剖分及加载约束方式如图1、图2，均采用8节点四边形单元进行人工剖分。东海陆架盆地区受菲律宾板块俯冲作用的影响，表现为近东西向的挤压作用。剖面模型的方向选为东西向。模型的深度方向定义为Y轴，铅直向下；X轴东西向，指向东。约束情况为：在模型底部施加Y方向约束；在模型的西南底角（即左下角）处施加全约束，这样的约束满足有限元分析的要求，即模型没有总体的平移和转动，能够对模型进行运算求解，得到收敛解答。虽然上述边界作用模型是以东海陆架盆地为背景，但砂泥岩剖面模型的构造作用方式都是类似的，差异只是边界构造作用力的大小。因此，上述剖面构造作用模型对砂泥岩剖面具有普遍意义。

在非线性弹性变形的条件下，地质体垂直方向的应力等于上覆地层的重力，水平方向的应力是水平重力应力分量（在重力作用下由泊松效应产生）和构造应力的叠加［21］，分别为：

式中：ρ为上覆岩石的平均密度，kg／m3；h为深度，m；g为重力加速度，m／s2；μ为岩石泊松比；n为与非线性压缩有关的常数，一般岩石采用0.67；σta和σti分别为水平方向的最大和最小构造应力，MPa。岩石密度平均约2.15×103kg／m3，重力加速度g取值10 m／s2。

模型顶部的上覆岩层压力由式（7）计算确定；模型东西边界采用两种不同的约束方式。模型Ⅰ采用位移约束方式通过不同缩短率确定；模型Ⅱ采用力约束方式，东西边界的受力大小由式（8）和式（9）计算确定。本次模拟中由于整个模型长度很小，所以东西边界施加的构造作用力是相等的；最大水平主应力的计算公式为式（8）；最大构造应力大小参考东海西湖凹陷黄岩构造中HY⁃1⁃1⁃1、HY⁃1⁃1⁃2、HY⁃2⁃2井压裂测试求得的结果确定。

2 模拟结果及分析

分别对两类模型的模拟结果进行分析，确定岩石力学参数、地层厚度对水平主应力的具体影响。

2.1 模型Ⅰ

研究表明，不同地应力状态下，杨氏模量和泊松比对水平主应力的影响程度是不一致的，下面分别加以阐述。

2.1.1 伸展应力状态下

当模型东西向缩短率为0.01%时，地层应力场处于伸展应力状态（最大主应力为直立）。模型Ⅰa的模拟计算结果（见图3）表明，水平主应力垂向上呈显著的差异，分界线决定于岩性的分界线。水平主应力随杨氏模量呈线性增大，其中最大水平主应力（σH）的递增速度，大于最小水平主应力（σh），表明杨氏模量对水平最大主应力的影响程度大于对最小水平主应力的影响程度。当杨氏模量增大3倍时，最大水平主应力增大1.2倍，最小水平主应力增大1.1倍。

模型Ⅰb的模拟结果（见图4）表明，水平主应力随泊松比呈类似指数关系增大，最小水平主应力的递增速度大于最大水平主应力，表明泊松比对水平最小主应力的影响程度大于对最大水平主应力的影响程度。当泊松比增大3倍时，最大水平主应力增大3.8倍，最小水平主应力增大4.8倍。

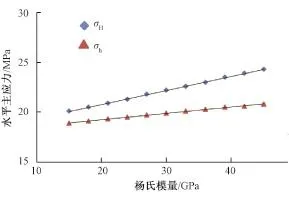
图3 伸展应力状态下杨氏模量与水平主应力关系Fig.3 Relationship between Young modulus and horizontal principal stress under extensional stress state

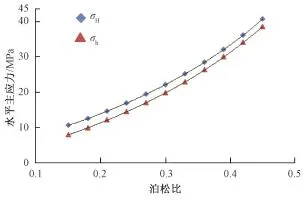
图4 伸展应力状态下泊松比与水平主应力关系Fig.4 Relationship between Poisson ratio andhorizontal principal stress under extensional stress state

伸展应力状态下，对比模型Ⅰa、Ⅰb的数值模拟结果可以看出，在杨氏模量和泊松比增大相同倍数的条件下，泊松比对最大水平主应力的影响程度大于杨氏模量对最大水平主应力的影响程度；同样，泊松比对最小水平主应力的影响程度也大于杨氏模量对最小水平主应力的影响程度。

随着岩石力学参数（杨氏模量或／和泊松比）的变化，水平主应力出现明显的分块特征，水平应力值的分界线与岩石力学性质的分界线一致（见图5）。对于走滑应力状态和挤压应力状态也是如此。

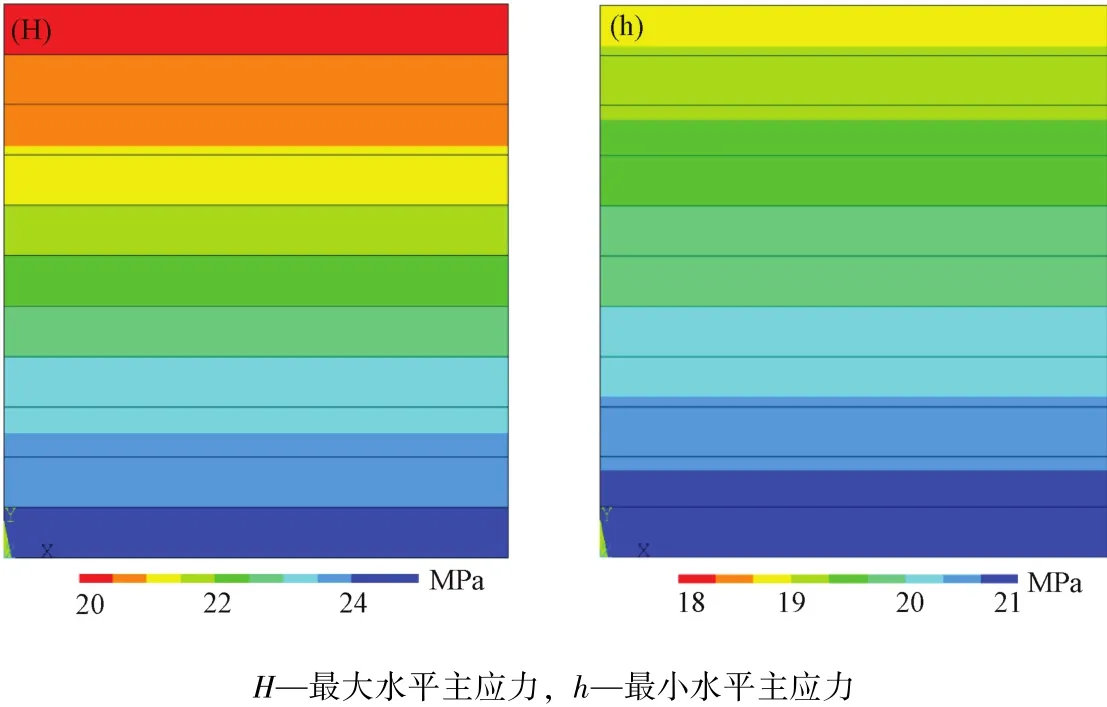
图5 在伸展应力状态下，模型Ⅰa水平主应力等值线分布Fig.5 Contour of horizontal principal stress for modelⅠa under extensional stress state

2.1.2 走滑应力状态下

当模型东西向缩短率为0.1%时，地层应力场处于走滑应力状态（中间主应力为直立）。模型Ⅰa的模拟计算结果（见图6）表明，杨氏模量对水平主应力的影响与在伸展应力状态下相似，也成线性关系。当杨氏模量增大3倍时，最大水平主应力增大2倍，最小水平主应力增大1.5倍。

模型Ⅰb的模拟结果（见图7）表明，泊松比对水平主应力的影响与在伸展应力状态下相似，也类似指数关系。当泊松比增大3倍时，最大水平主应力增大1.9倍，最小水平主应力增大4.4倍。

图6 走滑应力状态下杨氏模量与水平主应力关系Fig.6 Relationship between Young modulus and horizontal principal stress under strike⁃slip stress state

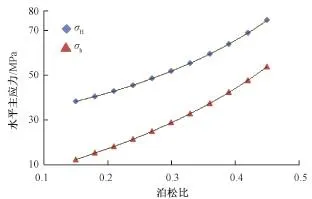
图7 走滑应力状态下泊松比与水平主应力关系Fig.7 Relationship between Poisson ratio and horizontal principal stress under strike⁃slip stress state

走滑应力状态下，对比模型Ⅰa、Ⅰb的数值模拟结果可以看出，在杨氏模量和泊松比增大相同倍数的条件下，泊松比与杨氏模量对最大水平主应力的影响程度基本相当；而泊松比对最小水平主应力的影响程度大于杨氏模量对最小水平主应力的影响程度。

2.1.3 在挤压应力状态下

当模型东西向的缩短率为0.3%时，地层应力场处于挤压应力状态（最小主应力为直立）。模型Ⅰa的模拟计算结果（见图8）表明，杨氏模量对水平主应力的影响，与在伸展应力状态下相似，也成线性关系。当杨氏模量E增大3倍时，最大水平主应力增大2.5倍，最小水平主应力增大1.9倍。

模型Ⅰb的模拟结果（见图9）表明，泊松比对水平主应力的影响，与在伸展应力状态下相似，也类似指数关系。当泊松比增大3倍时，最大水平主应力增大1.5倍，最小水平主应力增大4.1倍。

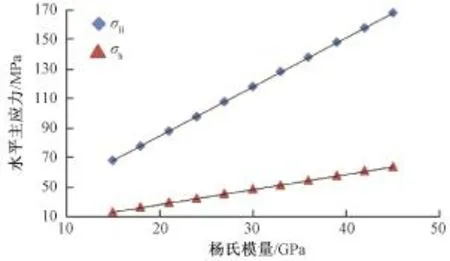
图8 挤压应力状态下杨氏模量与水平主应力关系Fig.8 Relationship between Young modulus and horizontal principal stress under compressive stress state

图9 挤压应力状态下泊松比与水平主应力的关系Fig.9 Relationship between Poisson ratio and horizontal principal stress under compressive stress state

挤压应力状态下，对比模型Ⅰa、Ⅰb的数值模拟结果可以看出，在杨氏模量和泊松比增大相同倍数的条件下，杨氏模量对最大水平主应力的影响程度大于泊松比；而泊松比对最小水平主应力的影响程度大于杨氏模量。

地层应力场由伸展应力状态转变为走滑应力状态再到挤压应力状态的过程中，杨氏模量对水平主应力的影响程度有逐渐增大的趋势，泊松比对水平主应力的影响程度有逐渐减小的趋势，但是在杨氏模量和泊松比增大相同倍数的条件下，泊松比对最小水平主应力的影响程度依然大于杨氏模量对最小水平主应力的影响程度。

上述研究结果确定了不同应力状态下杨氏模量和泊松比对水平主应力的定量影响。因此，在应力状态确定后，通过确定储层和隔层的力学参数（杨氏模量和泊松比），就可以分析储层和隔层水平主应力的分布特征（包括最小水平主应力差），从而可以为储层的压裂改造提供依据。

2.2 模型Ⅱ模拟结果及分析

在模型Ⅱa中，模拟计算求得旋回1、2、3地层分界面处的最小水平应力差分别为17.93 MPa、17.65 MPa、17.25 MPa。水平主应力分布出现明显的分块特征（见图10）。

在模型Ⅱb中，模拟计算求得在旋回1相邻层分界面处的最小水平应力差分别为4.41 MPa、4.13 MPa、4.40 MPa、4.70 MPa；旋回2相邻层分界面处的最小水平应力差分别为4.37 MPa、4.10 MPa、4.36 MPa、4.64 MPa；旋回3相邻层分界面处的最小水平应力差分别为4.31 MPa、4.04 MPa、4.36 MPa、4.64 MPa。

图10 模型Ⅱ最小水平主应力等值线分布Fig.10 Contour of minimum horizontal principal stress for modelⅡ

在模型Ⅱc中，模拟计算求得旋回1相邻层分界面处的最小水平应力差分4.47 MPa、4.20 MPa、4.46 MPa、4.75 MPa；旋回2相邻层分界面处的最小水平应力差分别为4.42 MPa、4.15 MPa、4.42 MPa、4.71 MPa；旋回3相邻层分界面处的最小水平应力差分别为4.36 MPa、4.09 MPa、4.37 MPa、4.66 MPa。

可以看出，岩石力学参数递变的层序小层之间的最小水平应力差远小于岩石力学参数突变的层序地层最小水平应力差，而小层间的最小水平应力差累积起来，与岩石力学参数突变的层序地层最小水平应力差相差不大；地层厚薄对最小水平应力差影响很小。

3 结论

水平主应力在垂向上的分布差异显著，呈现明显的分块特征，分界线决定于岩石力学性质的分界线。水平主应力随杨氏模量呈线性增大，杨氏模量对最大水平主应力的影响程度大于对最小水平主应力的影响程度。水平主应力随泊松比呈类似指数关系增大，泊松比对最小水平主应力的影响程度大于对最大水平主应力的影响程度。

伸展应力状态下，对两个水平主应力（最大和最小）的影响，泊松比均大于杨氏模量；走滑应力状态下，泊松比与杨氏模量对最大水平主应力的影响程度基本相当，而对最小水平主应力的影响，泊松比大于杨氏模量；挤压应力状态下，对于最大水平主应力的影响程度，杨氏模量大于泊松比，对于最小水平主应力的影响程度，泊松比大于杨氏模量。

地层的岩石力学参数变化对地层最小水平应力差产生显著影响，厚度变化对地层最小水平主应力差无影响。

［1］ Brown E T，Hoek E.Trends in relationships between measured in⁃situ stresses and depth［J］.International Journal of Rock Mechanics and Mining Sciences＆Geomechanics Abstracts，1978，15（4）：211～215.

［2］ Stacey T R，Wesseloo J.Updated in situ stress database for Southern Africa［M］.Proceedings and Monographs in Engineering，Water and Earth Sciences，2006：467～471.

［3］ Fuchs K，Muller B.World stress map of the earth：A key to tectonic processes and technological applications［J］. Natrwissen⁃schaften，2001，88：357～371.

［4］ Worotniki G，Denham D.The state stress in the upper part of the earth’s crust in Australia according to measurements in tunnels and mines and from seismic observation［C］∥Investigation of Stress in Rock⁃Advances in Stress Measurement.Sydney：Int.Soc.Rock Mech.Symp.，1976：71～82.

［5］ 朱焕春，陶振宇.不同岩石中地应力分布［J］.地震学报，1994，16（1）：50～62.

ZHU Huan⁃chun，TAO Zhen⁃yu.Geostress distribution in different rocks［J］.Acta Seismologica Sinica，1994，16（1）：50～62.

［6］ 景锋，盛谦，余美万.地应力与岩石弹性模量随埋深变化及相互影响［C］∥第十次全国岩石力学与工程学术大会论文集.2010：70～73.

JING Feng，SHENG Qian，YU Mei⁃wan.Change and rule of the geostress and the slastic modulus of rock with depth and their mutual impact［C］∥Symposium of The 11thNational Conference on Rock Mechanics and Engineering.2010：70～73.

［7］ 李新平，汪斌，周桂龙.我国大陆实测深部地应力分布规律研究［J］.岩土力学与工程学报，2012：31（增1）：2875～2880.

LI Xin⁃ping，WANG Bin，ZHOU Gui⁃long.Research on distribution rule of geostress in deep stratum in Chinese mainland［C］.Chinese Journal of Rock Mechanics and Engineering，2012，31（Supp.1）：2877～2879.

［8］ 赵德安，陈志敏，蔡小林，等.中国地应力场分布规律统计分析［J］.岩石力学与工程学报，2007，26（6）：1266～1270.

ZHAO De’an，CHEN Zhi⁃min，CAI Xiao⁃lin，et al.Analysis of distribution rule of geostress in China［J］.Chinese Journal of Rock Mechanics and Engineering，2007，26（6）：1266～1270.

［9］ 康红普，林键，张晓，等.潞安矿区井下地应力测量及分布规律研究［J］.岩土力学，2010，31（3）：828～831.

KANG Hong⁃pu，LIN Jian，ZHANG Xiao，et al.In⁃situ stress measurements and distribution laws in Lu’an underground coal mines［J］.Rock and Soil Mechanics，2010，31（3）：828～831.

［10］ 秦向辉，谭成轩，孙进忠，等.地应力与岩石弹性模量关系试验研究［J］.岩土力学，2012，33（6）：1690～1694.

QIN Xiang⁃hui，TAN Cheng⁃xuan，SUN Jin⁃zhong，et al.Experimental study of relation between in⁃situ crustal stress and rock elastic modulus［J］.Rock and Soil Mechanics，2012，33（6）：1690～1694.

［11］ 景锋，盛谦，张勇慧，等.中国大陆浅层地壳实测地应力分布规律研究［J］.岩石力学与工程学报，2007，26（10）：2057～2060.

JING Feng，SHENG Qian，ZHANG Yong⁃hui，et al.Research on distribution rule of shallow crustal geostress in China mainland［J］.Chinese Journal of Rock Machanics and Engineering，2007，26（10）：2057～2060.

［12］ Gudmundsson A.How local stresses control magma⁃chamber ruptures，dyke injections，and eruptions in composite volcanoes［J］.Earth⁃Science Reviews，2006，79：1～31.

［13］ Gudmundsson A，Simmenes T H，Larsen B，et al.Effects of internal structure and local stresses on fracture propagation，deflection，and arrest in fault zones［J］.Journal of Structural Geology，2010，32：1643～1655.

［14］ Gudmundsson A.Rock fractures in geological processes［M］.Cambridge University Press，2011：1～570.

［15］ 李道品，张连春.开发低渗透油田莫失良机［J］.中国石油企业，2004，（12）：44～45.

LI Dao⁃pin，ZHANG Lian⁃chun.Prospects for developing low permeability oilfields［J］.Chinese Petroleum Corporation，2004，（12）：44～45.

［16］ Tong H，Yin A.Reactivation tendency analysis：A theory for predicting the temporal evolution of preexisting weakness under uniform stress state［J］.Tectonophysics，2011，503：195～200.

［17］ Tong H，Wang J，Zhao H，et al.Mohr space and its application to the activation prediction of pre⁃existing weakness［J］. Science China：Earth Sciences，2014，57：1～10.

［18］ 陈子光.岩石力学性质与构造应力场［M］.北京：地质出版社，1986.

CHEN Zi⁃guang.Mechanical properties of rock and tectonic stress field［M］.Beijing：Geological Publishing House，1986：6～15.

［19］ 甘舜仙.有限元技术与程序［M］.北京：北京理工大学出版社，1988：243～299.

GAN Shun⁃xian.Finite element techniques and procedures［M］.Beijing：Beijing Institute of Technology Press，1988：243～299.

［20］ 潘别桐，黄润秋.工程地质数值法［M］.北京：地质出版社，1994：6～52.

PAN Bie⁃tong，HUANG Run⁃qiu.Engineering geological numerical method［M］.Beijing：Geological Publishing House，1994：6～52.

［21］ 童亨茂.断层开启和封闭的定量分析方法［J］.石油与天然气地质，1998，19（3）：215～220.

TONG Heng⁃mao.Quantitative analysis of fault opening and sealing［J］.Oil and Gas geology，1998，19（3）：215～220.

CHARACTERISTICS AND REGULARITY OF LONGITUDINAL GEOSTRESS DISTRIBUTION IN SAND⁃MUDSTONE STRATA

ZHANG Dong⁃tao1，2，TONG Heng⁃mao1，ZHAO Hai⁃tao3，LI Xue1，ZHANG Hao1

（1.State Key laboratory of Petroleum Resources and Prospecting，China University of Petroleum，Beijing 102249，China；2.Zhejiang Branch of China National Petroleum Corporation，Hangzhou 310023，China；3.School of Geology and Geomatics，Tianjin Chengjian University，Tianjin 300384，China）

Based on the analysis of basin geomechanics and mechanical properties of rocks，the characteristics and regularity of geostress distribution in the sand⁃mudstone strata are studied with numerical modeling by using the conceptual model of sand⁃mudstone strata abstracted from actual sedimentary strata.The results showed that horizontal principal stress mutates at the interface of sand⁃mudstone strata，and the change degree is mainly related to the difference of mechanical property of rock on both sides，then the regional tectonic stress.The effect of Young Modulus on the horizontal maximum principal stress is greater than that on the horizontal minimum principal stress；while the effect of Poisson Ratio on the horizontal minimum principal stress is higher than that on the horizontal maximum principal stress.The effect of Young Modulus and Possion Ratio on the horizontal maximum principal stress is different in different stress state.In extensional strike⁃slip and compressional stress state，Possion Ratio has greater roughly equivalent and samller effect on the horizontal maximum principal stress respectively.While，the effect of Possion Ratio on the horizontal minimum principal stress is always greater than that of Young Modulus in different stress state.The way of lithology changes in strata（mutations or gradient）has remarkable influence on the stress difference of horizontal principal stress，while the thicknesses no effect.The above understanding is valuable for effective reservoir hydraulic fracturing and reformation.

geostress distribution；numerical simulation；Poisson Ratio；Young Modulus；sand⁃mudstone

P553

A

1006⁃6616（2014）04⁃0352⁃11

2014⁃07⁃04

国家自然科学基金项目（41272160，40772086）；国家油气重大专项（2011ZX05006⁃006⁃02⁃01，2011ZX05023⁃004⁃012）

张东涛，男，硕士生，中石油浙江油田分公司助理工程师

童亨茂，E⁃mail：tonghm＠cup.edu.cn；tong⁃hm＠163.com