大膨胀率膨胀管的工艺参数优选及试验

张丛雷，李春福，张凤春，申文竹，宋开红，王燕群

（1.西南石油大学油气藏地质与开发工程国家重点试验室，成都610500；2.大港油田研究院，天津300280；3.天津大学机械学院，天津300072）①

大膨胀率膨胀管的工艺参数优选及试验

张丛雷1，李春福1，张凤春1，申文竹1，宋开红2，王燕群3

（1.西南石油大学油气藏地质与开发工程国家重点试验室，成都610500；2.大港油田研究院，天津300280；3.天津大学机械学院，天津300072）①

根据膨胀管膨胀过程的大塑性变形特点，讨论了膨胀管模拟过程中强化方式、应力-应变类型、膨胀锥半锥角以及膨胀锥膨胀区末端的倒角半径对膨胀载荷的影响，并把有限元模拟结果与膨胀试验数据进行对比分析。研究结果表明：倒角半径取值介于膨胀管膨胀前后管内半径之间时，膨胀载荷和膨胀锥的等效应力最小；采用真应力-应变曲线所得到的模拟结果与膨胀试验相比，误差较小，而采用工程应力-应变曲线和理想弹塑性力学模型进行模拟时，所得结果误差较大。

膨胀管；工艺参数；优化

实体膨胀管技术是21世纪初发展起来的，是可能广泛应用于复杂钻井、等径井以及水平井、大斜度井与特殊井完井的一项新技术［1-2］。到目前为止，该技术主要应用于10%左右的小膨胀率的套损井修井的套管补贴中［3-6］，而在膨胀率达20～30%的钻、完井应用领域的发展遇到瓶颈。究其原因是在大膨胀率下，井上所能够提供的动力远小于膨胀管膨胀所需要的动力。目前已有的可膨胀管膨胀过程的力学模型和有限元分析［7-11］，多数是建立在理想弹塑性力学模型或工程应力应变数据的基础上的，忽略或未完全考虑塑性阶段应力强化效应，造成分析结果与实际工程问题存在着较大的误差。因此，采用合理的有限元分析，为膨胀锥的设计、膨胀管的选材以及膨胀载荷的计算提供了可靠的依据。

本文针对新型膨胀管用钢07 M nSi双相钢，采用A N S Y S workbench14.5建立了膨胀管膨胀过程的三维模型，进行了大膨胀率膨胀管膨胀载荷计算、以及膨胀锥的锥角优化。并将模拟值与实验室膨胀试验数据相对照，得到了较为理想的结果。

1 大膨胀率膨胀管的有限元建模方法

1.1 模拟参数

本文选用07 M nSi双相钢进行有限元模拟。首先将冶炼的ø102 m m×6 m m的07 M nSi双相钢钢管分成3组，每组2根。第1组做球化退火，将其加热到720～930℃，保温48 h，随炉冷却至室温；第2组做完全退火，将其加热到930℃，保温3 h，随炉冷却至550℃，然后空冷；第3组做双相热处理，将其加热到740℃，保温40 min，然后淬火，再加热到180～200℃，保温4 h。其次，将以上管材按照相关标准制备成条状的拉伸试样进行拉伸试验，拉伸曲线图如图1。分别计算屈服强度（ReL）、抗拉强度Rm、断裂总延伸率At，而膨胀锥采用的是高强度诱导塑性钢（T RIP），数据结果如表1。因为钢材的弹性模量变化不大，在模拟时取206 G Pa，泊松比取0.3。

图1 07 M nSi钢不同热处理拉伸曲线

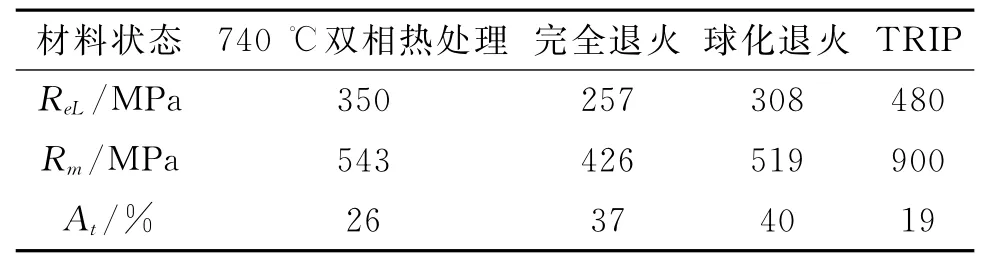
表1 拉伸试样数据

1.2 正确的应力应变数据输入与材料强化模型介绍

根据工程实践要求，实体可膨胀管在井下进行的套管补贴的膨胀率可达到10%～20%，而在等径井和复杂钻井等应用领域，极端的膨胀率可能达到30%。因此，膨胀管膨胀要经历塑性大变形和几何非线性过程。由图1双相钢拉伸曲线可知，在膨胀管膨胀过程中，膨胀管变形几乎全部处于强化阶段。如果膨胀率较大时，例如膨胀率大于20%，由单位体积应变能对膨胀力进行分析，可以发现采用工程应力应变或者采用理想弹塑性力学模型，其结果误差很大。因此，应输入真实的应力、应变数据。

强化模型的选择对膨胀前后应力分布，以及膨胀力的大小都有较大影响。A N S Y S W orkbench中常用的强化模型如图2，对于双线性随动强化模型和双线性等向强化模型，在模拟膨胀管膨胀过程中，参数只需要设定弹性模量、切线模量、泊松比。多线性随动强化模型和多线性线性等向强化模型，不仅需要用户输入弹性模量、泊松比，还可以允许用户输入多组不同温度下的拉伸曲线和每个拉伸曲线中的多个不同的应力-应变点。因此，可以比较全面地输入材料的拉伸数据。其中，随动强化模型主要用于小应变分析，而在大应变分析中很难收敛，因此不建议用于大应变分析［12］。对于双线性等向强化模型，由于只输入了弹性模量、切线模量、泊松比，因此在大膨胀率下，不能够准确地描述应力应变关系，且当膨胀率大于所对应的材料总延伸率时，应力会继续增加，造成结果远大于实际值。因此，在膨胀管模拟过程中，最好采用多线性等向强化模型，可以比较全面地反映材料在大变形下真实应力应变关系，使结果更加准确。

1.3 几何建模与边界条件约束

因膨胀管膨胀锥系统属于轴对称模型，为了简化计算和节省时间，采用A N S Y S W orkbench14.5建立膨胀管膨胀的1／4轴对称三维实体模型，如图3。边界条件为：在膨胀管下端表面，即在平面A B C上施加位移载荷，使该平面轴向位移为零，环向、径向自由；在膨胀锥下端表面即平面D E F上施加位移载荷，即在该平面上施加轴向位移，环向、径向位移为零；在四分之一对称面上施加Cycl ic Region对称边界条件。采用具有塑性、大变形及大应变能力的高阶三维20节点SO LID186单元；采用面面接触对，设置膨胀管内表面为接触单元C O N TA 174，设置膨胀锥从膨胀区到定径区的表面为目标单元TA R G E 170；对膨胀管和膨胀锥分别采用Swept M eshing网格划分和M ultiZone网格划分，其中膨胀管网格大小为壁厚的1／2，膨胀锥网格大小为6 m m；接触行为为非对称行为，选用Augmented Lagrange算法。

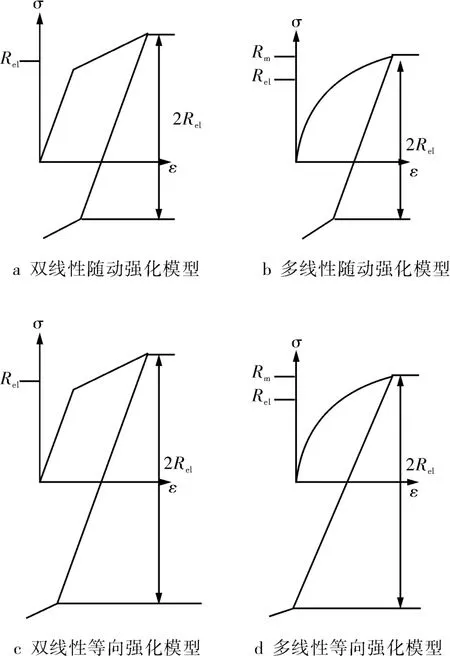
图2 A N S Y S W orkbench简化强化模型［12-13］

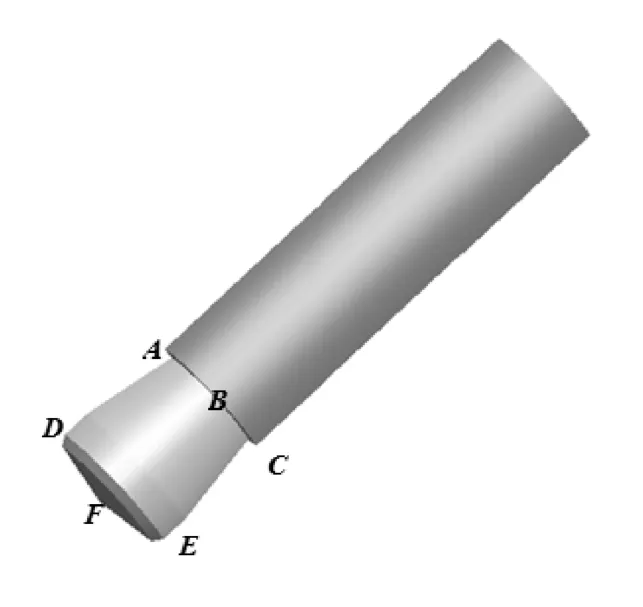
图3 膨胀管膨胀锥系统1／4轴对称模型

2 分析结果

2.1 不同膨胀锥倒角对膨胀过程的影响

目前，有关膨胀管膨胀的有限元模拟文献，在模拟中为简化计算，将膨胀锥作为刚体，未曾考虑膨胀管膨胀过程中膨胀锥的应力分布状况，以及对应应力状况下的膨胀锥优化。在实际膨胀过程中，膨胀锥表面会产生很多划痕，增加膨胀难度和减少膨胀锥的使用寿命。并且，在膨胀区向定径区过渡时，膨胀管管体要发生弯曲，曲率半径发生变化，应力变化剧烈。因此，需讨论该区域倒角半径对膨胀力以及在膨胀过程中对膨胀锥和膨胀管的应力分布的影响。

因膨胀管膨胀区向定径区过渡时，母线曲率半径在管半径（R0）到膨胀后管半径（R1）之间变化。因此，本文为了研究不同倒角半径对膨胀率以及膨胀过程中膨胀管膨胀锥系统中的应力分布的影响，分别模拟740℃双相热处理的ø102 m m×6 m m的07 M nSi双相钢，膨胀率为22.2%，定径段为20 m m，摩擦因数0.1，膨胀锥半锥角为12°；膨胀锥倒角半径为10、45、55 m m以及膨胀锥整个膨胀区为弧形过渡时，对膨胀过程的影响，如图4～8。

图4＝10 m m时膨胀管膨胀锥系统等效应力云图

图5＝45 m m时膨胀管膨胀锥系统等效应力云图

图6＝55 m m时膨胀管膨胀锥系统等效应力云图

图7 膨胀锥膨胀区为弧形过渡时膨胀管膨胀锥系统等效应力云图

图8 膨胀力随载荷步变化曲线

从图4～8中可以看出，倒角半径对膨胀过程膨胀锥的等效应力和膨胀力影响较大，且小的倒角很容易导致膨胀锥表面产生局部应力集中，导致膨胀过程中膨胀锥表面产生划痕，而较小的倒角对膨胀管的等效应力影响很小。其原因是：在膨胀区向定径区过渡时，管体要发生弯曲，初始弯曲从倒角起始处开始，弯曲产生的应力全部集中在倒角曲面上。倒角较小时，弯曲困难且曲面面积较小，应力较大；当倒角半径太大，如变成整个膨胀区弧形过渡时，会使接触面积大幅增加，膨胀力增加。因此，综合考虑倒角半径时，膨胀力和膨胀锥表面应力较小。

2.2 不同膨胀率下膨胀力与半锥角关系

为了研究不同膨胀率下，膨胀力与膨胀锥半锥角的关系，分别采用平面模型计算了07 M nSi钢材在不同膨胀率、摩擦因数、管材型号、膨胀锥半锥角下膨胀力的大小，其中＝R1，模拟参数如表2。不同热处理下膨胀力-锥角-膨胀率三者关系曲线如图9。

表2 膨胀管参数

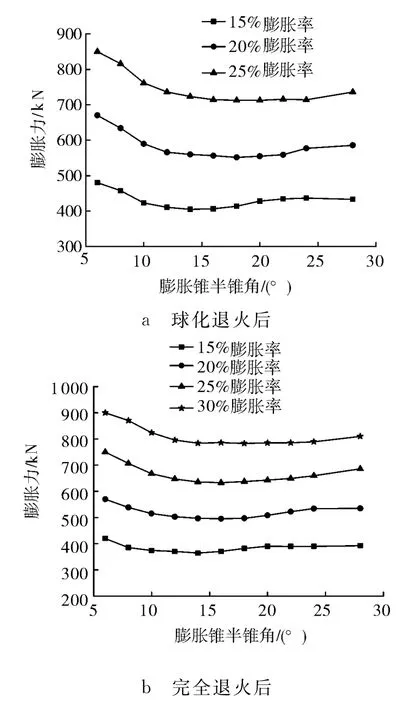
图9 不同热处理下膨胀力-锥角-膨胀率三者关系曲线

从图9可以看出，膨胀力与膨胀锥半锥角呈凹曲线关系；膨胀率为15%，膨胀锥最佳半锥角约为14°；膨胀率为20%，膨胀锥最佳半锥角约为16°；膨胀率为25%，膨胀锥最佳半锥角约为18°；膨胀率为30%，膨胀锥最佳半锥角约20°。另外，由于膨胀锥半锥角的增大，膨胀锥与膨胀管的接触面积逐渐减小，导致膨胀锥半锥角在12°～20°时，膨胀力变化很小。但是，通过模拟发现，角度太大时，在膨胀管末端，由于管体弯曲，膨胀管末端内表面紧紧包裹住膨胀锥，使结果难易收敛。因此，在膨胀锥设计时，角度可以选择在12～18°。

2.3 膨胀试验

对ø102 m m×6 m m的不同热处理的07 M nSi双相钢钢管进行膨胀，膨胀锥半锥角为12°，定径段长度为20 m m，内径膨胀率为22.2%，摩擦因数为0.1，其结果如表3。从表3可以看出，采用真应力-应变曲线模拟出来的结果和试验值符合的很好；采用工程应力应变数据模拟出来的数据比实际值较小，误差在15%左右；而采用理想弹塑性力学模型，不考虑材料强化现象，计算出来的结果与试验值相比较误差达25%以上。因此，在大尺寸大膨胀率下的膨胀管系统的设计、选材、模拟以及施工中，应考虑材料的强化效应，采用真实应力应变数据进行研究是非常重要的。

表3 膨胀管膨胀所需液压力的试验值与有限元模拟值

3 结论

1） 膨胀管膨胀是塑性大变形过程。通过模拟发现用真实应力、应变数据模拟的结果和试验值符合很好，而采用工程应力、应变数据和理想弹塑性力学模型模拟的结果误差很大。

2） 本文讨论了膨胀管膨胀过程中，膨胀锥膨胀区末端的倒角半径R对膨胀力以及膨胀锥和膨胀管的应力分布的影响。发现较小的半径容易引起该过渡段应力集中，在实际膨胀过程中有可能产生划痕。另外，较小或较大的倒角半径都会使膨胀力大幅增加。综合分析，在膨胀管膨胀时，该半径取值为时，膨胀力和膨胀锥的等效应力最小。

3） 通过模拟膨胀管在不同材料、尺寸、膨胀率、摩擦因数下膨胀力与膨胀锥半锥角的关系，得出膨胀锥的设计角度在12°～18°比较适宜。

［1］ 朱海波.膨胀筛管基管材料性能研究及应用［D］.成都：西南石油大学，2012.

［2］ 陈功剑，李春福，王朋飞，等.可膨胀管技术及其在石油工业中的应用［J］.石油仪器，2009，23（2）：65-67.

［3］ 胡慧莉.实体膨胀管补贴技术在冀东油田的应用［J］.吐哈油田，2011，16（4），395-398.

［4］ 王永刚，陶瑞东，李贵宾，等.实体膨胀管补贴套管技术在张海31-27井的应用［J］.石油天然气学报，2013，35（7）：141-144.

［5］ 肖进东，苏文红.吐哈油田膨胀管套管补贴技术应用［J］.中国新技术新产品，2012（20）：1170-118.

［6］ 胡石锋，孙婷，任丽华，等.实体膨胀管补贴技术在大港油田的应用与发展［J］.中国科技信息，2013（6）：82-83.

［7］ 龚龙祥，付建红，林元华等.膨胀套管膨胀力的理论计算［J］.钻采工艺，2006，29（4）：76-77.

［8］ 于桂杰，王瑞和，唐明.实体膨胀管理论膨胀载荷的确定［J］.石油钻采工艺，2010，32（2）：1-5.

［9］ 李涛，李富平，张立新，等.实体套管膨胀驱动力仿真研究［J］.石油矿场机械，2013，42（2）：39-42.

［10］ 蔡志安，李春福.孪生诱发塑性钢实体膨胀管膨胀有限元分析［J］.工程设计学报，2013，20（2）：236-239.

［11］ 郭慧娟，杨庆榜.实体膨胀管数值模拟及膨胀锥锥角优化设计［J］.石油机械，2010，38（7）：30-32.

［12］ A N S Y S结构非线性分析指南连载四［J／O L］.安世亚太，2007.

［13］ 于好善，王成彪，杨甘生，等.膨胀套管技术与膨胀成型仿真分析［J］.地质与勘探，2011，47（4）：693-697.

Optimization and Test of Process Parameters for Expandable
Casing with Large Expansion Rate

Z H A N G Cong-lei1，LI Chun-fu1，Z H A N G Feng-chun1，S H E NW en-zhu1，S O N G Kai-hong2，W A N G Yan-qun3
（1．The State Key Laboratory of Oil&Gas Reservoir Geology and E xploitation，South west Petroleu m University，Chengdu610500，China；2．D agang Oilfield Research Institute，Tianjin300280，China；3．M echanical College，Tianjin University，Tianjin300072，China）

According to the large plastic deformation characteristics of expansion tubular in expanding process，the im pacts of strengthening methods，stress-strain，semi-cone angle and cha mfering radius of expansion cone on expansion load have been discussed，and the differences of experimental and finite element sim ulation results have been co m pared and investigated.T he results prove that，the expansion load and the equivalent stress of expansion cone are both minimalif the cha mfering radius value is between the expansion pipe radius before and after the expansion.Co m paring the theoretical with experimental data of the true stress-strain curve，the result error is smaller，w hile the result errors of the engineering stress-strain data and ideal elastic-plastic mechanical m odel are too great.

expansion tubular；process para meter；optimizing design

T E931.207

A

10.3969／j.issn.1001-3482.2014.08.014

1001-3482（2014）08-0065-05

2014-01-11

张丛雷（1987-），男，四川阆中人，硕士研究生，目前从事膨胀管、膨胀锥系统力学分析和有限元模拟，E-mail：94602852＠qq.co m。