基于误差同步预测的SVM金融时间序列预测方法

李祥飞，张再生

(天津大学管理与经济学部，天津 300072)

基于误差同步预测的SVM金融时间序列预测方法

李祥飞，张再生

(天津大学管理与经济学部，天津 300072)

在现有支持向量机(SVM)方法的基础上提出对预测误差进行同步预测的双重预测方法，利用预测到的误差对初步预测值进行校正以提高预测精度．针对误差序列非线性、非平稳以及系统动力信息不足的特点，将经验模态分解(EMD)和支持向量机(SVM)方法结合引入误差序列的预测中．对误差序列的预测分别运用初步训练误差和测试误差对预测集合的误差进行预测，将所得到的误差序列分解为若干固有模态分量(IMF)，根据各个IMF不同尺度的特点，选择不同的参数对其进行预测，最终合成原始序列的误差预测值，将所预测到的误差与初步原始序列预测值结合，得到最终的预测值．仿真结果表明该方法能够很好地解决预测滞后性和拐点误差大的缺点，相对于普通的SVM预测方法具有更好的预测精度．

误差预测；经验模态分解；支持向量机；时间序列

金融时间序列的预测对于政府经济政策的颁布、企业和个体的投资活动具有至关重要的指导意义，但是复杂的内部规律和庞大的数据处理使得传统的预测方法效果不佳，因此新预测技术的提出和改进一直是金融时间序列研究的重要方向之一．目前主流的金融时间序列预测方法主要有模型法和数据挖掘2种．其中模型法是目前对时间序列进行深层次分析和刻画的主要方法，一些经典的时间序列分析模型如ARMA、ARCH、GARCH等已经被大量应用于金融时间序列预测中来．鉴于金融时间序列数据的强噪声特征，依靠从大量模糊的随机数据中提取隐含的有价值信息的数据挖掘技术最近更加受到关注．典型的数据挖掘技术主要有混沌理论、灰色理论、神经网络以及支持向量机(support vector machine，SVM).其中建立在统计学习理论基础上的SVM的提出和应用有着重要的意义，它在数据挖掘的基础上有效缩小了泛化误差的区间和模型的结构风险，同时又保证了样本预测误差最小[1]．从现有的研究来看，SVM在高位模式识别、函数拟合、时间序列预测方面表现出其独有的优势．基于该优势，SVM在金融时间序列的预测中也表现出较好的效果[2-3]．近些年来，基于SVM方法的金融时间序列预测出现了较多的变种，其中有多变量SVM[4]、小波SVM[5]和遗传算法SVM[6]等，这些在SVM技术上的改进方法使得预测精度相对于传统预测方法有了很大提高，但是现有方法仍未有效地解决SVM预测结果滞后性和拐点处误差较大的2个缺点，使得预测结果的指导意义仍受局限．

基于此，笔者在SVM预测的基础上提出了对SVM预测误差进行同步预测的“双重预测”法．为了克服误差序列多频带信息造成的干扰，在对预测误差进行预测时引入了经验模态分解(empirical mode decomposition，EMD)的方法．通过EMD方法将误差分解为具有不同尺度特征分量的叠加，对这些分量分别运用交叉验证法进行参数选择和预测，最终获得误差预测值．通过预测误差对初步预测值的校正后发现该方法能够有效地解决预测滞后和拐点误差的问题，预测精度也有了较大的提高．

1 SVM方法原理

SVM算法是由Cortes和Vapnik[7]于1995年在统计学理论基础上提出的一种新学习方法．SVM预测的基本思想是通过非线性映射φ将数据Xi映射到高纬度特征空间F中去，在此基础上进行线性回归．回归函数可以表示为

式中：φ(X)为Rm空间到F空间的非线性映射，X∈Rm；w为权向量；b为偏置水平．传统的预测方法即在集合F中寻找f∈F，使得结构风险值达到最小．结构风险公式可以表示为

式中：w2为置信风险；R[f]为经验风险；λ为常

emp数，用来平衡函数复杂度与损失误差；C(ei)为模型经验损失；e为样本的误差值；S为样本的容量．w2反

i映了模型的复杂程度，其值越小则置信风险越小．这样对于既定的损失函数，该类问题即可转化为二次规划最优解的问题，根据Vapnik的ε不敏感损失函数，定义为

ε控制回归的误差范围，其值越小精度越高，但是泛化能力减弱．基于该类损失函数则经验风险可以定义为

结合式(1)～式(4)，则原问题可以表示为最小化的线性风险泛函的问题，即

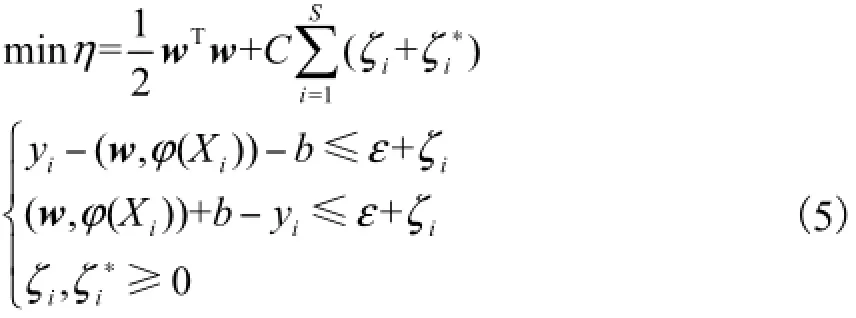
式中：C=1/λ；ε为估计的精度；ζi和ζi*为松弛变量.

为了便于求解将该类问题转化为对偶问题，即

对式(6)求解可以得到权向量w和偏置水平b，将其带入式(1)得非线性函数为

定义高维空间内积运算核函数为K(xi，xj)= k′( xi) k′( xj)，本研究采用径向基核函数Krbf(xi，xj)= exp(-γ‖xi-xj‖2)进行运算．根据Karush-Kuhn-Tucker定理求得α和α*，其中只有少数的α 和α*不为0，这些参数对应的样本在不灵敏边界上或外面的样本为支持向量，这时可以根据回归函数式f(X)对未知点进行预测．

2 EMD方法原理

EMD方法是Huang等[8-9]提出的一种信号处理方法．EMD方法的基本思想是：如果原始序列s(t)的极值点个数比过零点个数多2个以上，就需要进行处理．处理方法是找到原始序列s(t)的极大值点和极小值点，为了估计s(t)包络线的函数，采用三次样条插值法进行估计．取极大值和极小值包络线的平均值就得到了平均包络线m1(t)；原始序列S(t)减去该平均包络线m1(t)便得到了剔除低频数据分量的另一组序列h1(t)，即

如果h1(t)仍然不平稳，EMD的处理过程将继续，重复以上过程，原则上需要最终所得到的平均包络值为0为止．但是如果平均包络的平均值为0，则可能剔除掉了有幅度和频率调制的物理意义，因此将平均包络为0适当地调整为一个恰当的标准．即令

式中mk(t)为第k次循环的平均包络值．令SD介于0.1～0.2之间，这样的标准就适当放松了求平均包络的要求，也在一定程度上保留了IMF分量可能携带的物理意义．这样就得到了第1个分量C1(t)，即

C1(t)作为第1个分量其频率最高，用原始序列S(t)减去这一分量就得到“稍微”平稳的一组序列r1(t)．对r1(t)重复进行以上操作就可以得到第2个分量C2(t)和另一个序列r2(t)．如此重复下去就得到了一个不能再分解的序列rn(t)，这时EMD分解过程结束，最终的rn(t)代表了原始序列的总体趋势．

这时原始序列就分解成了IMF分量和总体趋势的叠加，即

本文运用EMD的过程实际上就是将股价训练误差和预测误差序列分解为具有不同时间尺度特征的分量叠加．在处理数据时，为了获得原始序列的真实信息，防止原序列极值端点问题给整个结果带来的“污染”，笔者采用多项式拟合算法对端点做了处理[10]．

3 预测模型概述

在运用SVM对时间序列进行预测的同时必然产生一定的误差，这些误差导致了预测结果的不理想．若对模型产生的误差也能够准确测量，那么将误差预测结果反馈后得到的预测值必然具有更高的精度．为此本研究提出了对误差进行同步预测的“双重预测”思想．值得注意的是，虽然SVM方法具有很强的泛化性，但是误差序列是一个具有很强随机性的序列，是一种多频谱交叠的信号．用单一的SVM模型只能拟合出系统的非线性，而误差序列的非平稳性可能使预测结果不理想，如果误差序列的预测有较大偏差，叠加之后会使得对预测序列的误差变得更大．因此，为了提高误差预测的精度，本研究采用EMD方法将误差序列分解为一系列具有不同时间尺度信息的分量集合．在此基础上针对不同尺度的信息对每一个信号分量选用不同的核函数和最优参数进行预测，最后将预测结果通过叠加得到误差的预测序列．本研究运用EMD与SVM结合的思路如图1所示．基本步骤描述如下.

步骤1 数据预处理．对于既定的一段股价时间序列{xt，t=1，2，…，n}，为满足支持向量机的分析方式，需要对该数据集进行空间重构，把时间序列转化为矩阵形式，构造样本(Xt，Yt)，其中Xt={xt-m，xt-m+1，…，xt-1}，Yt=xt．设m为滑动时间窗口大小，代表了用前m个交易日预测第m+1交易日价格．为了更好地利用现有数据对误差序列进行预测，需要针对原始序列进行分段处理，根据各阶段特征可以分为训练数据集A1、初步预测数据集A2和最终预测数据集A3.按空间重构原则分别对3个数据集合进行空间重构.

步骤2 原始序列初步预测．分别运用单一变量SVM和多变量SVM对原始序列A3集合数值进行初步预测，选择相对准确的初步预测值P(A3)．

步骤3 ,EMD分解误差并预测．设想在对A3集合的误差值进行预测时可以用到2种方法：①利用A1和A2集合的训练误差Et(A1，A2)建立SVM模型，对A3集合中误差值进行预测得到误差预测值Ep(A3)1；②对A1集合的误差集合建立对A2集合误差值的SVM模型，得到A2集合的误差预测值Ep(A2)，然后利用Ep(A2)的值建立SVM模型对A3集合误差进行预测，得到预测值Ep(A3)2．本研究将①中对误差预测并对初始预测值进行校正的方法称为训练误差预测与校正(training error prediction & correction SVM，TEPC-SVM)；将②中的方法称为测试误差预测与校正(forecast error prediction & correction SVM，FEPC-SVM)．

步骤4 参数确定．参数的选择对于SVM预测的精度和泛化能力具有决定性的影响．关于SVM参数的选择尚未有统一的最好方法，当前最多被认可和广泛使用的方法就是交叉验证法(cross validation，CV)．交叉验证是Hills[11]提出的对泛化误差的无偏估计．本文采用K折交叉验证法(K-CV)选择参数，这样可以保证较高的分类准确率以及避免数据挖掘技术导致的学习状态不稳和维度灾难等问题[12].

步骤5 数据预测．带入参数，得到误差预测结果并校正初始预测值．分别获得A3集合的初步预测值P(A3)以及误差预测值Ep(A3)1和Ep(A3)2．利用Ep(A3)1和Ep(A3)2分别对初步预测值P(A3)进行校正，从而得到校正后的预测值P*(A3)1和P*(A3)2．

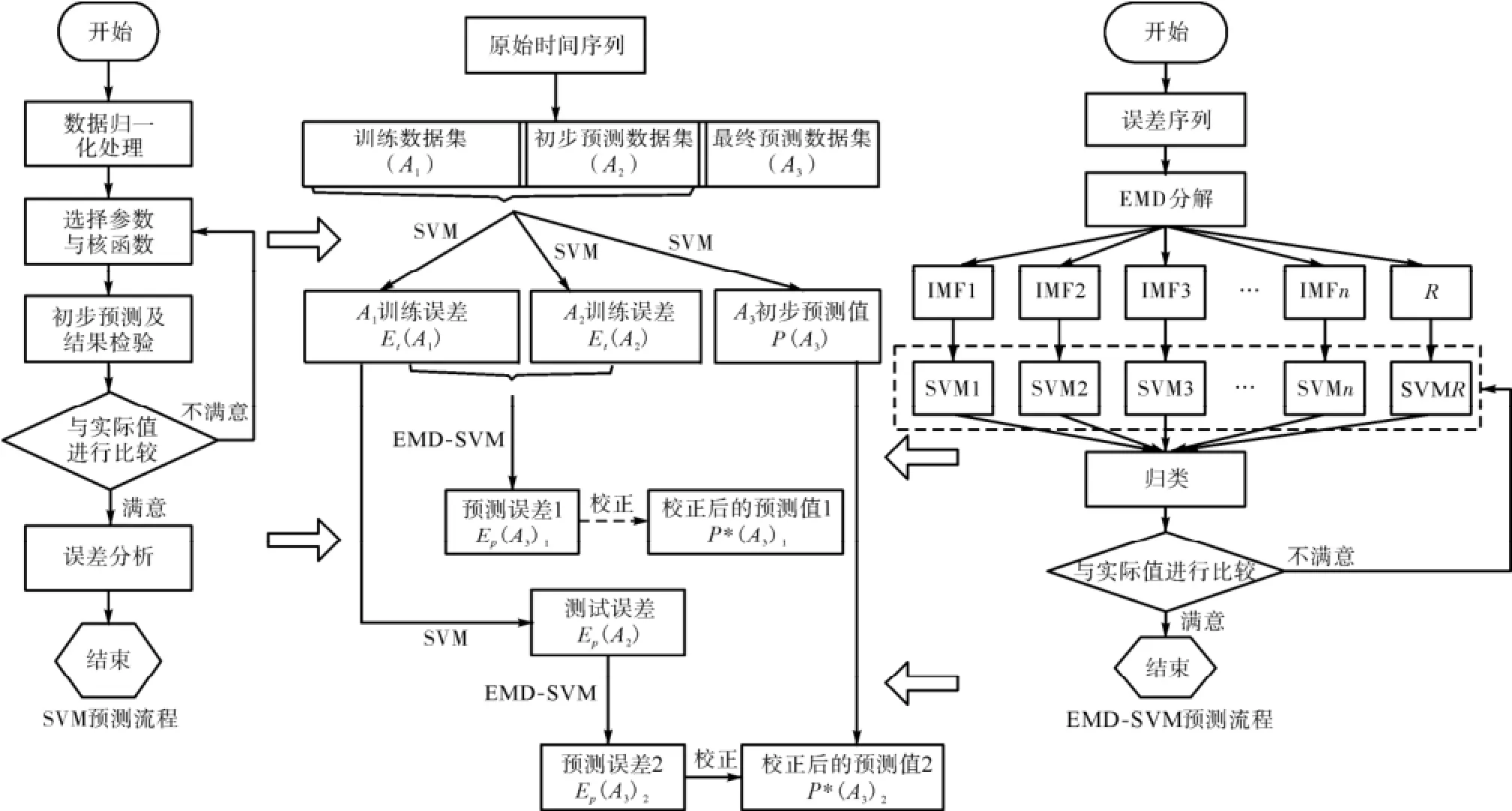
图1 预测模型结构Fig.1 Structure of forecast model

4 预测方法实例分析

4.1 数据样本的选择

本文研究样本选取上证A股指数2011年1月4日至2012年10月22日的收盘数，为了检验本方法对个股的预测能力，笔者随机选取了工商银行(601398)2011年1月4日至2012年10月22日的收盘数作为样本．2个观测样本均为437个交易日．令m=4，即用前4天的股票收盘价格预测第5天的收盘价格．数据来源于国信证券金太阳网上交易专业版软件．

4.2 初步预测

股价时间序列是一种有着极强特殊性的序列数据，其变化趋势要受到各种因素的影响．由于SVM方法的特点，现有对股价多运用的是单影响变量的预测方法．然而由于变量之间相互影响，现实中股价是要受多个变量影响，变量之间存在极强的相互依赖关系，仅由单一变量建立回归预测模型很可能无法准确预测其变化趋势，导致预测结果不理想．因此，为了提高初始预测的精度，本文选取单一变量SVM和多变量SVM预测结果的最优值作为对原始序列的初步预测值．

利用样本数据的A1集合和A2集合建立支持向量机预测模型，对样本集A3进行预测，选取K折交叉验证法确定训练的最优参数，步骤如下.

步骤1 对样本数据做归一化处理，变换至[0，1]区间．

步骤2 将参数进行原始化，选取罚函数c和核函数g的取值范围，并将其网格化搜索．采用K-CV法将训练数据平均分为K组，记为train(1)，train(2)，…，train(K)．K个组的数据中分别令每一组做测试数据集，剩余的K-1组做训练数据集，这样需要进行K次运算，K次运算对应的准确率分别为acc(1)，…，acc(K)．最后运用这K组准确率的平均值作为K-CV分类器性能衡量指标．运用K-CV对本文选取的2类样本的单一变量和多变量SVM进行参数选择，结果如图2所示.

图2 初步预测K折交叉法最优参数选择Fig.2 Preliminary prediction K folding bracketing method optimal parameter selection

如图2所示，横纵坐标分别为c和g的对数，取值范围均为[-4，4]，竖坐标选用均方误差．在横纵坐标形成的网格范围内进行离散化搜索，选取最佳的c和g组合使得MSE的绝对值达到最小．若针对最小MSE出现多个c和g组合，则选择具有最小c值的组合，原因是过大的c值可能导致预测模型过学习状态的产生．

步骤3 将最优参数带入SVM预测模型，通过对训练集数据进行训练获得对未来股价的初步预测值．在进行数据训练时对本模型采用时间窗滚动，即将本点的实际数据视为已知数据滚入训练样本集，去除时间最远点，重置训练后得到下一步的股价预测结果．单一和多维变量的SVM预测结果如图3所示．

初步的SVM模型预测曲线表明，单一维度和多维度的变量预测对于上证A股指数和随机选取的601398个股均能准确地反映原始序列的变化趋势.但是上述提到的2个问题非常明显：预测曲线相对于实测曲线具有非常明显的滞后性，这主要体现在单一维度的SVM预测上；多维变量的SVM预测方法虽然在一定程度上减弱了预测结果的滞后性，但是在拐点处仍存在着较大的误差．对于误差的测量，笔者选用均方误差(RMSE)、平均绝对误差(MAE)以及平均绝对百分比误差(MAPE)3类指标．各指标计算公式分别为

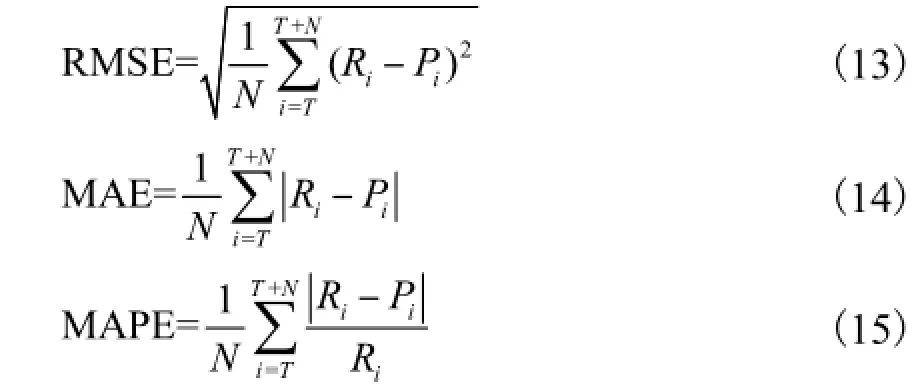
式中：Ri为预测的实际值；Pi为预测值；T为训练数据集合的时间长度；N为预测集合的时间跨度．为了更加准确地分析两类方法的优劣，分别计算上证A股指数和601398预测结果的3类误差，并将其反映至表1.

总体上来说，相对于单一维度的SVM预测，多变量SVM的误差相对更小一些，因此本研究运用多变量SVM的预测结果作为对原始序列的初步预测值P(A3)．虽然多变量SVM体现出了一定的优势，但是根据图3和表1的结果，多变量SVM方法仍然无法有效克服拐点误差较大的缺点．采用预测误差修正后，这一缺点有望得到解决．

图3 单一和多维变量对两类股票价格的初步预测结果Fig.3 Preliminary prediction results of single and multidimensional variable SVM method

表1 初步预测结果误差测量Tab.1 Error measurement of preliminary prediction

4.3 EMD-SVM误差预测模型及误差校正

本文中出现的两类误差序列具有很强的随机性，难以选取具有相同时间尺度特征的影响因素．因此本研究针对EMD分解后的各IMF分量采用上述的K-CV方法进行参数寻优，以获得各个不同分量的预测值．由于本研究拟采用2种误差预测方法，所以需要对训练误差和测试误差分别进行EMD分解．如前面建立模型步骤中描述的，2种误差序列得到的预测值中训练误差的预测值记为Ep(A3)1，预测误差的预测值记为Ep(A3)2．

对上证A股指数(A1，A2)集合区间的训练误差和A2集合区间的预测误差进行EMD分解，得到图4所示的各个固有模态分量IMF和剩余分量R叠加．误差预测和校正后的预测结果如图5所示．

如图4所示，TEPC-SVM方法将训练误差序列分解之后得到7个IMF分量以及1个剩余分量，FEPC-SVM方法将预测误差序列分解后得到5个IMF分量和1个剩余分量．运用上述交叉验证法获得最优的训练参数，运用各自的最优参数分别对各分量进行训练，将各分量的预测值叠加，获得最终的误差预测结果Ep(A3)1和Ep(A3)2，将其反馈到初始预测序列P(A3)中，得到校正后的预测值P*(A3)1和P*(A3)2．图5的预测结果表明，对于上证A股指数，校正后的预测值与误差预测值的趋势具有较高的一致性，在误差的预测值高于实际误差值的时间点上，校正后的预测值会显著高于实际值．可以看出，TEPC-SVM和FEPC-SVM两类预测方法均取得了较好的效果，预测结果滞后性和拐点误差的问题得到了很好的解决，说明了TEPC-SVM和FEPC-SVM方法在对股票大盘的预测中具有较好的应用前景，但仅从图形判断难以断定哪种方法更有优势．

重复以上步骤，对601398个股(A1，A2)集合的训练误差和A2集合的预测误差分别进行EMD分解，得到图6所示的各个固有模态分量IMF和剩余分量R，误差预测和最终预测结果如图7所示．

如图6所示，对于601398，TEPC-SVM训练误差分解之后得到7个IMF分量以及1个剩余分量，FEPC-SVM预测误差分解得到6个IMF分量和1个剩余分量．对各分量运用交叉验证法获得各自最优参数进行训练和预测，图7的结果显示，601398的预测结果滞后性和拐点误差的问题同样得到了明显改善．不同于上证A股指数，从图形上来看，在对601398个股的预测上，FEPC-SVM相对TEPC-SVM更有优势．

图4 上证A股误差EMD分解及SVM训练Fig.4 EMD decomposition and SVM training of the Shanghai A-share

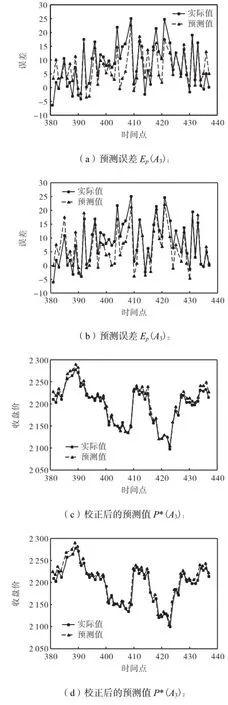
图5 上证A股误差预测结果及校正后的预测值Fig.5 Error prediction results of Shanghai A-share and predicted values after correction

为了更好地衡量和比较2种误差预测方法的预测能力，将2类方法预测结果的3类误差测量值列出，如表2所示．

图6 601398误差EMD分解及SVM训练Fig.6 EMD decomposition and SVM training of the 601398 share

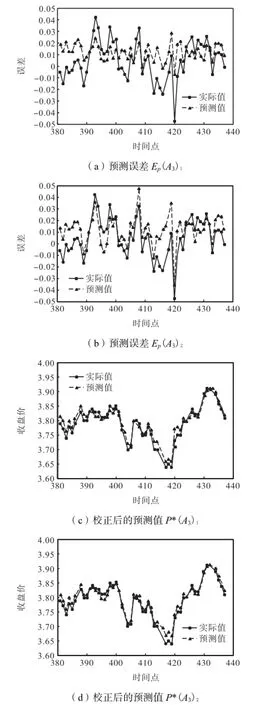
图7 601398误差预测结果及校正后的预测值Fig.7 Error prediction results of the 601398 share and predicted values after correction

可以发现，2类方法对于上证A股指数和601398均具有较强的泛化能力和预测准确性．不同的是对于大盘指数的预测而言，TEPC-SVM与FEPC-SVM两类方法各有所长；对于个股的预测结果则有明显的差异：FEPC-SVM要明显优于TEPCSVM．原因可以解释为SVM模型在用于预测之前是由训练数据进行训练而建立的，产生误差是已知样本的拟合误差，该误差与预测样本的预测误差具有相似性取决于模型是欠训练还是正常训练而有所不同，而测试样本和预测样本对于SVM模型来说都是未知样本，因此它们的误差具有更相似的规律和特性．

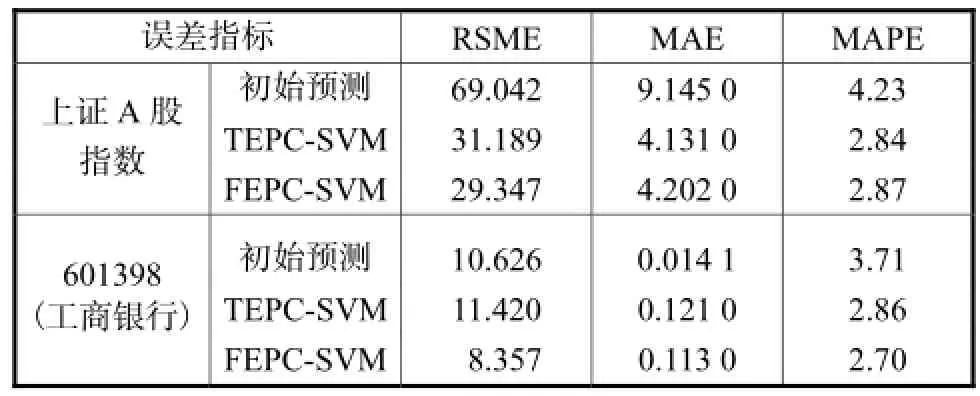
表2 误差预测校正方法预测结果误差测量Tab.2 Error measurement of prediction after correction

5 结 语

本文在SVM数据挖掘技术的基础上提出了一种改进方法，即在对原始时间序列进行预测的同时，对可能产生的误差同步进行预测．需注意的是，在对误差序列进行预测时，考虑到误差序列的随机性强，相邻频带的干扰可能造成误差序列无法体现反映全部的系统动力信息．基于EMD多分辨率的特征，本研究提出将EMD的方法引入对误差的预测上来，建立了基于EMD和SVM方法融合的预测模型．该模型使误差信号中包含的信息通过各基本模态分量得到充分体现，简化了时间序列各尺度分量特征信息的干涉或耦合．对本研究选取的上证A股指数和随机选取的个股601398进行仿真测试，结果表明该预测模型能够有效解决预测结果滞后和拐点误差的问题，体现了该类方法的良好应用前景．限于篇幅，本研究并未对其他大盘股指数和个股进行测试．进一步增加测试样本的数量和测试范围，探讨该模型的适用性将是未来研究的重要方向之一．

［1］ Vapnik V. The Nature of Statistical Learning Theory[M]. New York：Springer-Verlag，1999.

［2］ Tay F，Cao L. Modified support vector machines in financial time series forecasting[J]. Neurocomputing，2002，48(1/2/3/4)：847-861.

［3］ Thissen U，van Brakel R，de Weijer A P，et al. Using support vector machines for time series prediction[J]. Chemometrics and Intelligent Laboratory Systems， 2003，69(1/2)：35-49.

［4］ 金 桃，岳 敏，穆进超，等. 基于SVM的多变量股市时间序列预测研究[J]. 计算机应用与软件，2010，27(6)：191-194.

Jin Tao，Yue Min，Mu Jinchao，et al. On SVM-based multi-variable stock market time series prediction[J]. Computer Applications and Software，2010，27(6)：191-194(in Chinese).

［5］ 杨 稣，史耀媛，宋 恒. 基于小波变换域的SVM股市时间序列预测算法[J]. 科学技术与工程，2008，8(12)：3171-3175.

Yang Su，Shi Yaoyuan，Song Heng. Stock market time series prediction method based on SVM and wavelet[J]. Science Technology and Engineering，2008，8(12)：3171-3175(in Chinese).

［6］ 李 军，赵 峰. 基于支持向量回归神经网络的时间序列预测[J]. 系统仿真学报，2008，20(15)：4025-4030.

Li Jun，Zhao Feng. Time series prediction using support vector regression neural networks[J]. Journal of System Simulation，2008，20(15)：4025-4030(in Chinese).

［7］ Cortes C，Vapnik V. Support-vector networks[J]. Machine Learning，1995，20(3)：273-297.

［8］ Huang N E，Shen Z，Long S R，et al. The empirical mode decomposition and the Hilbert spectrum for nonlinear and non-stationary time series analysis[J]. Proceedings of the Royal Society A：Mathematical，Physical and Engineering Sciences，1998，454(1971)：903-995.

［9］ Huang N E，Shen Z，Long S R. A new view of nonlinear water waves：The Hilbert spectrum[J]. Annual Review of Fluid Mechanics，1999，31：417-457.

［10］ 刘慧婷，倪志伟，李建洋. 经验模态分解方法及实现[J]. 计算机工程与应用，2006，42(32)：44-47.

Liu Huiting，Ni Zhiwei，Li Jianyang. Empirical mode decomposition method and its implementation[J]. Computer Engineering and Applications，2006，42(32)：44-47(in Chinese).

［11］ Hills M. Allocation rules and their error rates[J]. Journal of the Royal Statistical Society，Series B：Methodological，1966，28(1)：1-31.

［12］ Du H F，Gong M G，Jiao L C，et al. A novel artificial immune system algorithm for high-dimensional function numerical optimization[J]. Progress in Natural Science，2005，15(5)：463-471.

(责任编辑：孙立华)

Support Vector Machine Method for Financial Time Series Prediction Based on Simultaneous Error Prediction

Li Xiangfei，Zhang Zaisheng
(College of Management and Economics，Tianjin University，Tianjin 300072，China)

A double prediction method by means of synchronous prediction of the prediction error was proposed based on the existing support vector machine (SVM)method, and the predicted error was used to correct the preliminary predicted values in order to improve the prediction accuracy. Considering that the error sequence may have features of non-stationarity, nonlinearity system and insufficient information of system dynamics, the empirical mode decomposition (EMD) method was used and embed into the support vector machine method to predict the error series according to the preliminary training error and test error respectively. In order to get the final prediction error, different parameters were chosen to forecast the error sequence decomposed into several intrinsic mode function(IMF) components according to the different scale characteristics of each IMF. The final prediction results were obtained by using prediction error to correct the preliminary predicted values. Simulation results show that the new method which can solve the problems of forecast hysteresis and inflection point error effectively has better prediction precision.

error prediction；empirical mode decomposition；support vector machine；time series

TP181

A

0493-2137(2014)01-0086-09

10.11784/tdxbz201211039

2012-11-21；

2013-03-15.

国家自然科学基金资助项目(70971097).

李祥飞（1986— ），男，博士研究生，soar.li@163.com.

张再生，zhangzs@tju.edu.cn.