晶界能各向异性晶粒长大的计算机模拟

王 浩，张金山，宗喜梅，牛晓峰，许春香，赵达文

（1.太原理工大学，山西太原 030024；2.太原科技大学，山西太原 030024）

正常晶粒长大可以发生在形变试样初次再结晶后续过程中，即发生于形变试样初次再结晶完成后的退火过程中，也可以发生于无原始形变试样的退火处理过程中[1]。晶粒长大过程中微观组织的演化直接影响着多晶材料的性能，晶粒的平均晶粒尺寸，晶粒尺寸分布，晶粒形状和结构等参数与多晶材料的力学性能有着密切关系。由于晶粒长大过程中微观组织演化的物理实验研究难度大、耗时费力，计算机模拟的应用为组织演化的研究提供了一种有效的途径[2]。

截止目前，已有多种模型应用于晶粒长大的模拟过程中，其中比较常见的有相场法、蒙特卡洛法、元胞自动机法（CA）[3,4]等。CA的优势在于描述复杂物理系统离散空间、时间上的演化规律，具有很高的效率和三维扩展性，由于其灵活性及编程容易实现性，CA在凝固[5]、再结晶[6]、晶粒长大等方面都有广泛的应用。本文通过CA模型研究了正常晶粒长大过程，探讨了晶粒相貌，晶粒长大动力学及拓扑学关系。所得结论与理论预测及实验研究得到的结果相符合，对于晶粒长大控制有一定参考意义。

1 元胞自动机模型的建立

1.1 转变规则的确定

正常晶粒长大的元胞自动机转变规则大多基于Metropolis算法（模拟退火算法），本文在Metropolis算法基础上，引入晶界能各向异性函数，由此得到改进后基于晶界能各向异性的CA转变规则如下：

（1）遍历全部元胞，如果搜索到晶界元胞，计算当前元胞i与邻居元胞之间的能量Ei,old：

式中：δ为Kronecker δ函数；j为元胞i的第j个邻居；Si为元胞i的取向数；Sj为元胞i的第j个邻居的取向数；为元胞i与其第j个邻居元胞之间的晶界能。

考虑到晶界能的各向异性，引入晶界能的表达式如下所示[7]：

式中：θm为大角度晶界，本文取 15°；γm为大角度晶界能，本文选取0.625 J∙m-2；为当前元胞与第j个邻居元胞的取向差，当0≤θ≤π时，=θ，当π＜θ≤2π，=2π－θ。

（2）判断转变之后的能量差ΔE。找到与当前元胞取向数不同的邻居元胞，将新的取向值赋予当前元胞，计算转变之后新的能量Ei,new，得到ΔE＝Ei,new－Ei,old。

（3）概率性转变机制。若ΔE＜0，则使系统自由能降低，此时状态转变的概率p=1；若ΔE=0，此时系统自由能不变，元胞状态可能转变也可能保持原来状态，此时给定状态转变的概率p=0.125（1/8,Moore型邻居元胞数的倒数）；若ΔE＞0时，系统的自由能升高，不接受此时的转变，元胞保持原来的状态，此时状态转变的概率p=0。总的来说，元胞的转变规则可以表示为：

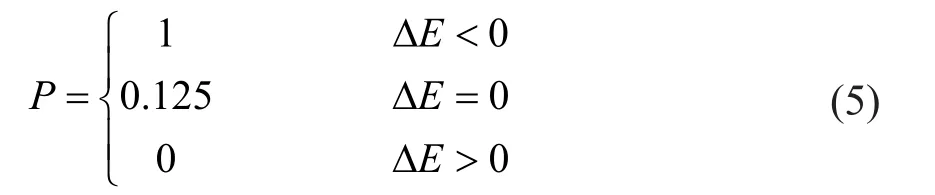
1.2 模拟初始参数设定

本文选取模拟区域为0.6 mm×0.6 mm，将模拟区域划分为300×300的网格，每个网格的尺寸为2 μm，邻居类型采取Moore型，边界条件为周期性边界条件。J.GEIGER等人[8]研究表明：当取向数大于64时，可以有效地避免这种碰撞后晶粒变大的现象。因此，在本文中设定最大取向数Q为96。考虑到模型的随机性，取3次模拟结果的统计平均值作为模拟定量结果。

2 模拟结果与讨论

2.1 晶粒显微组织演化

图1所示为晶粒长大过程中不同时刻的晶粒组织演化图。可以看出，随着模拟时间的增加，大晶粒逐渐长大，小晶粒逐渐缩小，平均晶粒尺寸增大，总的晶粒数量减少，晶界趋于平直，在晶粒长大过程中观察到两个重要的拓扑变化：晶粒的消失，即大晶粒通过吞噬小晶粒而长大；晶粒邻居的变化。

2.2 晶粒长大动力学

晶粒正常长大服从幂函数关系动力学[9]，如图2所示为晶粒尺寸随模拟时间的变化及其对数分析曲线，其中拟合对数分析曲线得到的斜率即为晶粒长大指数。

图1 不同时间步晶粒长大组织演化

从图2.a知，在模拟开始阶段处于不稳定阶段，当模拟时间步（CAS）大于100步后基本进入稳态长大阶段。由图2.b得到的晶粒长大指数为0.399，得到的晶粒长大指数比理论值低，因为理论值是在理想条件下得到的，在实际实验及模拟中受到晶界能各向异性的影响，实验值和模拟值比理论值略低。模拟得到的晶粒长大指数与Hsun Hu, B.B.Rath[10]研究等温条件下铅的晶粒长大指数0.4接近；比等温条件下锆的晶粒长大指数0.35略高。此外，晶粒长大指数的大小受到多个因素的影响，比如模拟时间步，模拟区域大小，转变规则，元胞尺寸等。

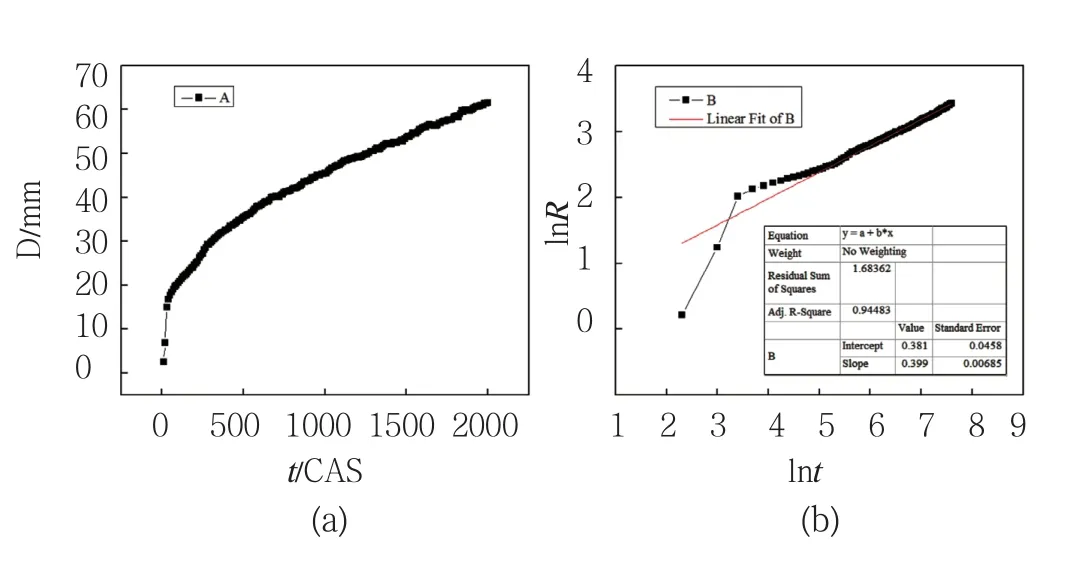
图2 平均晶粒尺寸随模拟时间变化(a)，及其对数分析曲线lnR-lnt图(b)

2.3 相对晶粒尺寸及晶粒边数的分布

通过对CA模拟结果的统计分析，得到了晶粒尺寸分布和晶粒边数分布，如图3所示。从图3.a以看出，最大频率在（R/Rm）≈1.0，说明大多数晶粒尺寸分布于平均晶粒尺寸附近。当（R/Rm）＞2.6的晶粒出现频率很低，即没有出现异常长大的晶粒，这进一步表明晶粒的生长特点符合正常长大规律。从图3.b看出，晶粒边数基本上分布在4～8之间，边数小于3和大于9的晶粒很少，其中6边形晶粒最多。从图中可以看出，不论是晶粒尺寸分布曲线还是晶粒边数分布曲线，不同时刻分布曲线的重合度非常高，说明晶粒尺寸分布、晶粒边数分布具有很好的时间不变性特点，模拟结果与正常晶粒长大理论相符合。

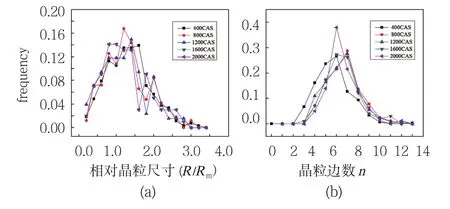
图3 不同模拟时间步的晶粒统计分析(a)相对晶粒尺寸分布；(b)晶粒边数分布

3 结论

（1）考虑实际晶体中晶界能的各向异性，引入晶界能各向异性函数，建立了晶界能各向异性的二维元胞自动机模型，得到了晶粒组织演化图，此模型具有更好的物理基础。

（2）模拟得到的晶粒生长指数为0.399，并与实验值进行了对比，模拟结果能准确反映晶粒生长动力学规律。

（3）晶粒拓扑结构变化主要表现为晶粒的消失和晶粒邻居的变化。晶粒长大过程中大晶粒吞并小晶粒，平均晶粒尺寸增大，晶粒组织中6边形晶粒居多，晶粒尺寸分布和晶粒边数分布呈现了时间不变性。本文的CA模型能为等温退火晶粒组织演化的控制提供一定指导作用。

[1]毛卫民，赵新兵.金属的再结晶与晶粒长大[M].北京:冶金工业出版社, 1994:218.

[2]高冠会，臧加伦.计算机凝固模拟技术在铸造工艺优化中的应用[J].中国铸造装备与技术，2010(4): 52-54.

[3]RAGHAVAN S, SAHAY S S.Modeling the topological features during grain growth by cellular automaton[J].Computational Materials Science, 2009, 46(1): 92–99.

[4]麻晓飞，关小军，刘运腾，等.改进转变规则的晶粒长大CA模型 [J].中国有色金属学报，2008，18(1)：138–144.

[5]LIU Ying, XU Qing–yan, LIU Bai–cheng.A Modified Cellular Automaton Method for the Modeling of the Dendritic Morphology of Binary Alloys[J].Tsinghua Science and Technology, 2006, 11(5):495–500.

[6]周盛，傅建，王涛.基于CA法对叶片成形中动态再结晶的模拟研究[J].热加工工艺，2009,38(5):96-100.

[7]DAVIES C H J.Growth of nuclei in a cellular automaton simulation of recrystallisation[J].Scripta Materialia, 1997, 36(11): 35–40.

[8]GEIGER J, ROÓSZ A, BARKÓCZY P.Simulation of grain coarsening in two dimensions by cellular-automaton[J].Acta Materialia, 2001,49(4): 623–629.

[9]YU Qiang, ESCHE SK.A Monte Carlo algorithm for single phase normal grain growth with improved accuracy and efficiency[J].Computational Materials Science, 2003, 27(3): 259–270.

[10]Hsun Hu, B.B.Rath.On the time exponent in isothermal grain growth.Metallurgical Transactions, 1970, 11(1): 3181-3184.