一种基于多阶段数据的实航工作可靠度评估方法

廖富魁, 周春明, 赵 敏

(1. 海军驻昆明750试验场 军事代表室, 云南 昆明, 650051; 2. 昆明船舶设备研究试验中心, 云南 昆明, 650053)

一种基于多阶段数据的实航工作可靠度评估方法

廖富魁1, 周春明2, 赵 敏2

(1. 海军驻昆明750试验场 军事代表室, 云南 昆明, 650051; 2. 昆明船舶设备研究试验中心, 云南 昆明, 650053)

基于产品研制不同阶段的实航试验数据, 运用顺序约束的二项分布可靠性阶段增长模型和贝叶斯统计方法, 建立了一种实航工作可靠度评估方法, 有效解决了研制不同阶段产品技术状态变化造成实航试验数据不能用于可靠性评估的问题, 提高了实航试验数据的利用效率, 能够客观、经济地评价实航工作可靠度。

实航试验; 可靠性评估; 贝叶斯统计

0 引言

实航工作可靠度是水中兵器可靠性评定中的一个十分重要的指标, 客观、经济地评价实航工作可靠度, 一方面可为部队平时训练和作战使用提供指导, 另一方面可为研制生产单位提供改进依据, 同时, 也可为上级机关的决策提供有力支撑, 因此, 实航工作可靠度是一个倍受关注的指标。但在水中兵器研制过程中, 由于水中兵器结构复杂功能多, 再加之受试验考核条件限制, 实航工作可靠度的试验、考核与评估是一项难题。

近年来, 众多研究者针对实航工作可靠度考核与评价中的不足, 从故障的多状态判定、功能的不同划分与处理、基于实航时间等不同角度出发, 开展了不同的评定方法研究[1-3], 取得了可喜的成果。本文在总结这些研究成果的基础上, 基于产品研制全过程的实航试验数据, 运用顺序约束的二项分布可靠性阶段增长模型进行科研试验数据的综合, 获取科研先验信息, 解决研制中技术状态的变化和可靠度变化的问题, 运用贝叶斯统计方法, 将科研先验信息与定型试验数据相结合, 建立了一种实航工作可靠度评估方法, 这种评估方法, 具有较强的理论依据和工程应用价值,便于工程使用。同时, 充分运用了产品研制全过程的实航试验信息, 提高了试验数据的利用效率,评定结果更接近实际。

1 评估流程

1.1 研制过程的实航试验

在水中兵器研制过程中, 一般情况下, 开展实航试验的过程有方案阶段、初样机研制阶段、正样机研制阶段和定型阶段。分析这些阶段的实航试验可发现许多潜在的、有价值的信息和数据特点, 详见图1所示。

图1 试验阶段及数据图Fig. 1 Schematic multi-stage sea trial data

1) 方案阶段、初样机研制阶段、正样机研制阶段的实航试验属科研试验范畴, 其目的是通过实航试验激励故障发生, 不断发现设计、试制中的质量问题, 并采取有效措施, 不断改进, 从而提高产品的可靠度。这一过程是一个产品技术状态不断变化的过程。

2) 定型阶段是确定产品的技术状态, 考核产品可靠性所达到水平的过程。但是, 由于现代水中兵器的结构复杂、功能多, 集声、电、机等多技术于一体, 试验考核难度巨大。同时, 受研制周期、研制经费、试验条件等诸多因素的影响,实航试验的次数有限, 属小子样试验数据, 仅用定型实航试验数据评估产品的可靠度水平, 其评估的充分性有所欠缺, 同时, 对实航试验数据信息的运用不够充分。

3) 各阶段的实航试验数据不仅反映了当前阶段的技术状态和可靠性水平, 同时, 也反映了研制过程的技术状态和可靠性水平的变化趋势。

1.2 评估思路

为了客观、经济地进行实航工作可靠度评估,高效运用各阶段实航试验数据是一种行之有效的办法, 这就需要评估技术方法的支撑。一般来说,高效运用数据必须运用以下3方面的信息。

1) 来自总体分布信息, 即总体分布或总体所属分布族所给出的信息。对于水中兵器的实航试验来说, 现阶段能用做法是将试验结果可判定为成功和失败, 即实航试验结果符合二项分布。

2) 来自研制过程的实航试验先验信息。来自于研制各阶段科研实航试验数据和先验分布的信息, 从方案阶段、初样机研制阶段和正样机研制阶段都需要进行实航试验, 但是, 产品的技术状态是变化的, 可靠性水平也是变化, 运用可靠性增长方法, 将数据转换到定型前试验信息, 这就解决了产品的技术状态变化, 同时可靠性水平也变化的问题。

3) 来自样本的信息。产品需要进行定型实航试验考核, 这是来自于定型实航试验的样本数据信息, 是十分有价值的数据。

基于多阶段数据的实航工作可靠度评估方法应将这3种信息有机结合, 才可客观评价实航工作可靠度, 评估流程见图2所示。

图2 评估流程图Fig. 2 Flow chart of assessment

具体做法是:

a. 数据收集。收集方案阶段、初样机研制阶段、正样机研制阶段、定型阶段的实航试验数据, 其中方案阶段、初样机研制阶段和正样机研制阶段作为先验数据, 定型阶段数据作为当前样本数据;

b. 获取等效先验数据。运用顺序约束的二项分布可靠性阶段增长模型, 将方案、初样和正样3个阶段的先验数据等效到定型前的状态, 获取等效先验数据;

c. 获取综合等效试验数据。运用贝叶斯评估方法, 将等效先验数据和当前样本数据进行综合,得到实航试验的综合等效试验数据;

d. 运用综合等效试验数据进行实航工作可靠度计算。

2 评估方法

2.1 增长评估方法

即可用依据各阶段的试验信息进行综合, 顺序约束的二项分布可靠性阶段增长模型进行可靠性增长分析和确定产品最后阶段的可靠度[4], 其模型为

若 Pi≤α , 则认为从阶段i及 i+ 1, 可靠性增长, 否则, 将两阶段的数据合并, 再与下阶段作增长检验, 这里, 显著性水平α常取0.2。

最后阶段的综合信息为

式中,μ, γ是Rm的1阶、2阶矩, 且

其中

2.2 贝叶斯评估方法

贝叶斯统计分析集中了总体、先验和样本 3种信息中关于θ 的一切信息, 而又排除了一切与θ 无关的信息之后得到的结果, 对θ 进行统计推断更为有效和合理。对于成败型二项分布, 如果试验次数为 n, 成功次数为 s, θ 为待估参数, 其分布函数为[5-6]

为了充分运用先验数据, 选先验分布为共轭先验分布, 为贝塔分布β (a, b), 选定参数a, b后,可得θ 的后验分布为

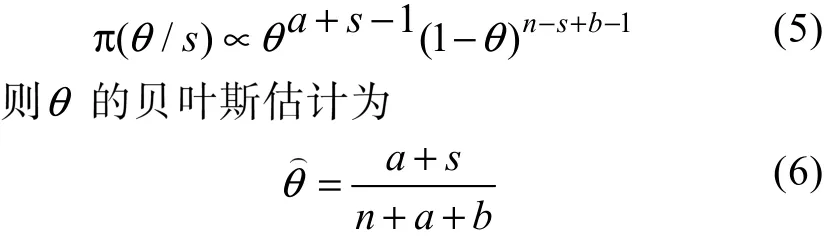
参数 a, b的统计意义是: 在过去的试验中,试验成功次数为a, 失效次数为b, 将此结果与现有的结果合并, 得总试验次数为 n+a+b, 成功次数为a+s, 于是得到可靠度的估计值。

2.3 试验参数确定方法

θ 的共轭先验分布贝塔分布β (a,b), 其两参数的概率密度函数为

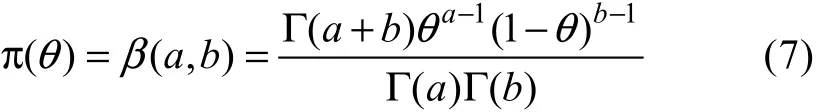
为了有效运用贝叶斯统计, 需利用先验信息确定先验分布中超参数 a, b, 一般方法有先验矩法、先验分位数法、先验矩法和先验分位数法、先验矩法和使用者对其的确信度法等方法, 而在实航工作可靠度评估工程实际中, 先验矩法更易实施[6]。

对于式(8)先验信息是经顺序约束的二项分布可靠性阶段增长模型分析得到的等效先验数据,仅有一个, 不能计算获得有效的先验信息矩, 故作特殊情况处理, 处理方法如下。

当i=1时, 2阶矩不存在, 从式(8)1阶矩有

于是, 通过式(6)、式(9)获得综合实航试验数据为

2.4 实航工作可靠度计算方法

贝叶斯统计的区间估计有多个方法, 为了工程实践中便于计算和结果比较, 建议采用经典二项分布计算[7], 其计算公式为

式中:RL为可靠度置信下限值; α为置信度;ss为综合试验成功数;ff为综合试验失败数;nn为综合试验次数。

3 算例

某产品的研制经历了阶段 1、阶段 2、阶段3, 最终开展了定型试验考核, 各阶段都开展实航试验, 试验结果如表1所示。

表1 实航试验结果Table 1 Data from sea trial

从表1数据可知, 定型阶段数据属小子样试验数据, 仅用其评估产品的可靠度水平, 其评估的充分性有所欠缺。因此, 将阶段1、阶段2和阶段3数据作为先验数据, 运用前述理论和公式,与定型阶段进行数据综合, 以及定型的可靠性评估。

首先, 对表1所示数据进行阶段1～阶段2、阶段 2～阶段 3阶段的增长分析, 可得 P1=0.1, P2=0.1。

取显著性水平为0.2, 则阶段1～阶段2、阶段2～阶段3阶段可靠度都增长。

运用顺序约束的二项分布可靠性阶段增长模型将阶段1、阶段2、阶段3数据进行综合, 得到等效先验数据为sa=178.0, fa=1.5, na=179.5。

运用贝叶斯统计将等效先验数据与定型阶段数据进行综合, 得到综合等效试验数据为 ss=193, ff=2.5, nn=195.5。

取可靠性置信度为 0.8, 于是得到产品的最终实航工作可靠度RL0.975。

4 结束语

水中兵器的实航工作可靠度是一个倍受各部门关注的重要指标, 众多的研究者为了实现客观、经济地评估实航工作可靠度, 开展了大量的研究, 建立了关注不同方面的评估方法。本文从方案阶段、初样机阶段、正样机阶段开展实航试验的研制实际出发, 运用顺序约束的二项分布可靠性阶段增长模型, 进行研制全过程的实航试验数据综合, 通过可靠度增长的分析, 获取科研先验信息, 有效解决了研制不同阶段产品技术状态的变化造成的实航试验数据不能用于可靠性评定的问题, 同时, 运用贝叶斯统计方法, 将科研先验信息与定型实航试验数据相结合, 建立了一种实航工作可靠度评估方法, 这种评估方法, 具有较强的理论依据和工程应用价值, 并能充分运用产品研制全过程实航试验信息, 提高了试验数据的利用效率。

[1] 周春明. 多状态鱼雷可靠性的评定方法[J]. 鱼雷技术, 2010, 18(6): 419-421.

Zhou Chun-ming. Reliability Estimation Method of Torpedo in Multimode Condition Test[J]. Torpedo Technology, 2010, 18(6): 419-421.

[2] 贺成刚, 叶豪杰, 张迪. 一种改进的鱼雷实航工作可靠度评定方法[J]. 鱼雷技术, 2011, 19(6): 411-414.

He Cheng-gang, Ye Hao-jie, Zhang Di. An Improved Method for Evaluating Torpedo′s Working Reliability in Sea Trial[J]. Torpedo Technology, 2011, 19(6): 411-414.

[3] 周春明, 吕宏. 基于航行时间的水下航行体可靠度评定方法[J]. 鱼雷技术, 2012, 20(4): 241-244.

Zhou Chun-ming, Lü Hong. A Reliability Evaluation Method for Underwater V ehicle Based on Running Time[J]. Torpedo Technology, 2012, 20(4): 241-244.

[4] 周源泉.质量可靠性增长与评定方法[M]. 北京:北京航空航天大学出版社, 1997: 242-245.

[5] 茆诗松, 汤银才, 王玲玲. 可靠性统计[M]. 北京: 高等教育出版社, 2008: 379-389.

[6] 茆诗松. 贝叶斯统计[M]. 北京:中国统计出版社, 2005:13-15.

[7] 周源泉, 翁朝曦. 可靠性评定[M]. 北京: 科学出版社, 1990: 72-79.

(责任编辑: 许 妍)

An Assessment Method for Operational Reliability in Sea Trial Based on Multi-stage Experimental Data

LIAO Fu-kui1, ZHOU Chun-ming2, ZHAO Min2
(1. Navy Representative Office Stationed in Kunming 750 Test Range, Kunming 650051, China; 2. Kunming Shipborne Equipment Research & Test Center, Kunming 650053, China)

For solving the problem that the sea trial data cannot be used in operational reliability assessment due to the change of product technical condition in different stages, an assessment method for operational reliability in sea trial based on multi-stage sea trial data is presented by using the reliability stage growth model with ordered constraint binomial distribution and the Bayesian statistics. Application results show that this assessment method can improve the utilization of the data from sea trial, and assess the operational reliability objectively and economically in sea trial.

sea trial; reliability assessment; Bayesian statistics

TJ631.6

A

1673-1948(2014)02-0145-05

2013-05-30;

2013-08-08.

廖富魁(1963-), 男, 硕士, 高级工程师, 研究方向为项目质量管理与可靠性管理.