近场条件下脉冲基线定位性能影响因素分析

董利英, 陈志菲

(西北工业大学 自动化学院, 陕西 西安, 710072)

近场条件下脉冲基线定位性能影响因素分析

董利英, 陈志菲

(西北工业大学 自动化学院, 陕西 西安, 710072)

针对近场条件下的脉冲基线定位, 推导了以脉冲前沿到达时刻为变量的测距和测向公式, 讨论了CW脉冲信号参数、阵列参数和声源入射位置对其定位性能的影响。仿真结果表明, 较低的脉冲辐射频率, 较大的阵列孔径, 以及声源从阵列正对方向入射时, 脉冲基线定位具有更好的定位性能, 阵元数对其定位性能影响不大, 随着声源与阵列距离的增大, 定向性能大致保持不变, 而测距性能则不断下降。

脉冲基线定位; 近场; 定位性能

0 引言

目前, 水下运动目标跟踪定位方法大致分为2类, 一类是基于阵列信号处理, 尤其是自适应波束形成类方法, 典型应用如声纳、拖曳线列阵等[1]; 另一类是脉冲基线定位, 如超短基线定位系统等[2]。这 2类方法大多针对中远程目标, 其中基于阵列信号处理方法根据应用背景的不同, 对阵列孔径、阵元数等阵列参数要求较高。脉冲基线定位方法利用脉冲参考源信号到达各阵元时刻的不同,构造非线性方程组来定位目标, 算法简单, 所需阵元数少, 且对脉冲信号频带要求较低。

脉冲基线定位是一种基于到达时间差(time difference of arrival, TDOA)的定位方法, 目前广泛应用的三元阵方法即属此类[3]。当阵元数更多时, 需要求解最小二乘(least square, LS)意义下的定位结果[4-6]。现有的三元阵和多元阵 TDOA方法本质上都是利用已知的阵列几何关系, 以及通过广义互相关等方法估计的两两通道间的时延差来定位。但是在近场运动目标的噪声源识别中,需要精确估计目标航迹以便对接收信号解多普勒,为此需要在定位的同时估计声源辐射时刻, 即脉冲基线定位。本文在水下近场环境下讨论了影响脉冲基线定位性能的各种因素, 包括CW脉冲参数, 基线阵列以及声源位置等, 以便根据不同环境选择合适的CW脉冲和阵列参数。

1 脉冲基线定位方法

如图1所示, 假设有M+1个阵元构成的线列阵采集近场点声源辐射的 CW 脉冲信号(M≥2 ),阵列位于x轴上, 其中一个阵元位于坐标原点。对于接收的CW脉冲信号, 脉冲基线定位有[7]

式中: c为声速, Sm=(xm, ym, zm)和tm分别是第m个阵元的空间坐标和接收到的脉冲信号前沿到达时刻, (xs, ys, zs)和ts则是声源辐射该脉冲时的空间坐标和辐射时刻, 且xs, ys, zs和ts未知, 阵元坐标Sm已知,脉冲前沿到达时刻 tm可由接收信号的时域处理得到。当有4个以上阵元时, 上式成为超定方程组, 从而解得声源坐标(xs, ys, zs)和辐射时刻ts。

图1 脉冲基线定位示意图Fig. 1 Schematic of pulse baseline positioning

式(1)构成的非线性方程组是 TDOA类方法的核心, 作为非凸问题其求解多采用非线性最小二乘类方法, 并且在双曲线交汇或者球面交汇的准则下有不同的解法, 通常球面交汇类方法性能更加稳定[4,8]。TDOA类方法都是直接利用两两通道间的时延差进行定位, 但是广义互相关等时延估计方法无法给出到达时刻, 而式(1)的脉冲基线定位方法通过估计脉冲前沿到达时刻可以确定辐射时刻。此外, ts可由(xs, ys, zs)解得, 因此式中仅有未知量(xs, ys, zs), 即三元阵可实现脉冲基线定位。下面给出以到达时刻tm为变量的测距和定向公式, 并分析影响其tm估计精度的因素。

根据图1将式(1)转换到极坐标下, 有

式中: r=c(t0−ts)和θ分别为声源距离和入射方向,为声源到达原点处阵元的时刻; rm为声源到第m个阵元的距离; Dm为各阵元到坐标原点的距离, 其中

上式可变成

将式(4)代入式(2)得

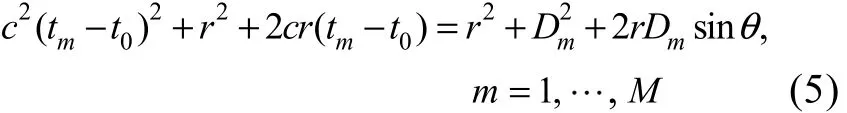
相应的第m+1个等式为

式(5)乘以Dm+1, 式(6)乘以Dm后两式相减整理得

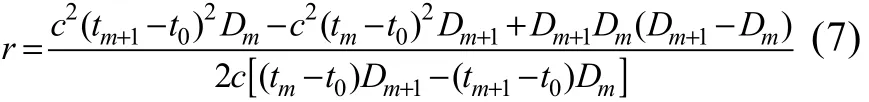
当图 1为三元均匀线列阵, 阵元间距d= Dm+1−Dm时, 式(7)变成

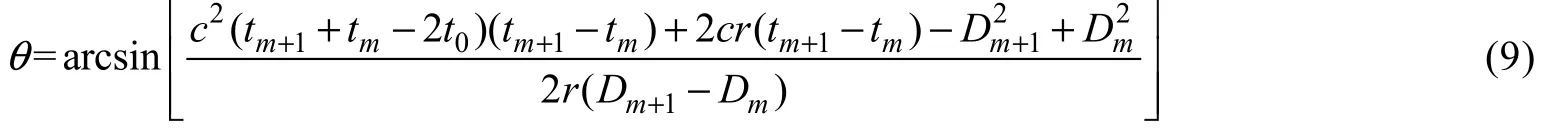
这里不再将式(7)代入上式, 以简化公式表达。

文献[3]和[9]分别给出了近场和远场条件下三元阵方法的测距和测向偏差, 脉冲基线定位方法与三元阵方法相似, 影响其定位性能的主要因素是时延差估计, 即各阵元的脉冲前沿到达时刻估计。图2给出了某次试验中CW脉冲前沿到达时刻估计示意图, 这里将各通道的归一化幅度进行了平移, 以更好地表现各通道脉冲前沿时刻的差异。首先以脉冲波形第1峰值点对应时刻作为前沿时刻的粗略估计, 而后以该峰值点为起点截取其后的正弦脉冲波形, 估计其初相位对应的时延量τm来修正前沿时刻的估计, 即

图2 脉冲波形前沿到达时刻估计示意图Fig. 2 Schematic of estimation at the arrival time of leading pulse

由于离散采样的原因, 从第1峰值点往后截取的正弦脉冲波形的初相位φm=2πfcτm不为零, 因此τm=φm/(2πfc)可用于补偿脉冲前沿时刻估计, 其中 fc为 CW 脉冲信号载频。τm的求解涉及到 φm和 fc的估计, 其中 fc已知, 但运动声源存在时变多普勒频移Δf(t)。这里可假定多普勒频移为常数Δfm, 使接收信号频率变为fm=fc+Δfm, 即

此外, 采用FFT估计φm时通常取最大谱峰点的相位, 然而FFT频谱存在频谱泄露, 使得最大峰值点对应频率并非fm或fc, 造成φm的估计偏差也较大。

本文采用复合复比值法估计脉冲波形载频fm,全相位方法估计其初相位 φm, 两者均针对最大谱峰附近数据进行处理, 且估计过程相互独立[10-11]。全相位法适合在中高信噪比下估计正弦信号的相位, 其估计结果受频谱泄露影响较小, 频谱泄露较大时全相位法性能优于FFT的相位估计精度。复合复比值法本质上是利用频域复数加权插值来估计频率, 性能优于FFT的估计结果。

2 仿真结果与分析

脉冲基线定位方法对阵列和环境参数的要求要低于传统的阵列定向方法, 但是阵列参数、脉冲信号参数等条件对其定位性能还是有一定影响。本节以均匀线列阵(uniform linear array, ULA)为例通过仿真来说明信噪比(signal to noise ratio, SNR)、脉冲信号频率fc、阵列孔径D、阵元数M、声源入射方向θ和声源距离r等参数对脉冲基线定位的影响。

假定xy平面内ULA置于x轴, 阵列中心为坐标原点O, 声源与坐标原点O的连线与y轴的夹角为入射方向θ。 图3首先给出了100次Monte Carlo试验后直接FFT, 以及基于全相位和复合复比值法这2种脉冲前沿时刻估计方法的定位性能,显然后者提高了脉冲基线定位性能。

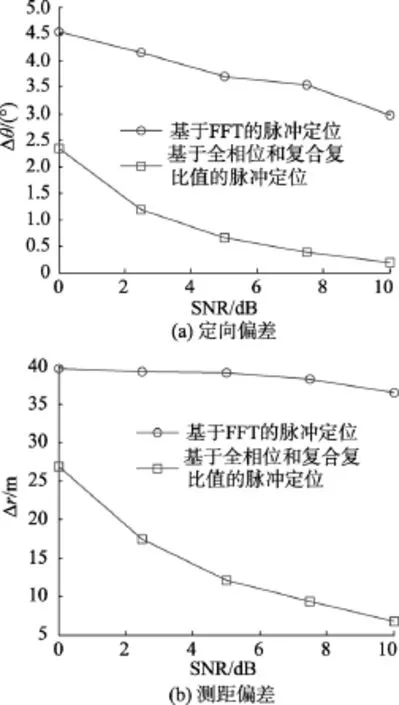
图3 静止CW脉冲的脉冲基线定位性能示意图Fig. 3 Schematic of pulse baseline positioning performance for static CW pulse

图4给出了不同信噪比不同入射方向时100次Monte Carlo试验后脉冲基线定位的定向偏差Δθ和测距误差 Δr, 其中 CW 脉冲的频率为 fc= 0.1fs, fs为采样频率。显然, 随着信噪比的提高,定位偏差不断减小, 而在入射方向上, 阵列正对区域的定位偏差较小。

图5给出了不同脉冲频率不同声源距离时, 100次Monte Carlo试验后脉冲基线的定位性能,其中脉冲声源位于y轴上, 声源距离是指声源与坐标原点O之间的距离, 其他环境参数与上文相同。随着频率的下降, 脉冲基线定位方法的定位偏差不断减小, 这是由于相对于高频信号, 低频CW脉冲的每个正弦信号周期内有更多地采样点,这样脉冲前沿时刻估计更精确, 从而提高了定位性能。另一方面, 随着声源距离的增大, 定向偏差变化不大, 测距偏差在上升。

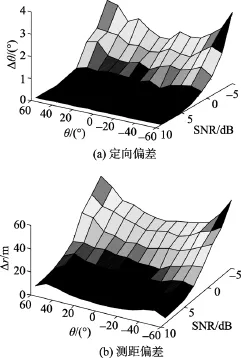
图4 不同信噪比与入射方向时脉冲基线定位性能示意图Fig. 4 Performance of pulse baseline positioning with different signal to noise ratios and incident directions

图5 不同脉冲频率与声源距离时脉冲基线定位性能示意图Fig. 5 Performance of pulse baseline positioning with different pulse frequencies and source ranges

上文给出了脉冲信号参数对基线定位性能的影响, 下面讨论阵列参数对其的影响。图6给出了不同阵元数M不同阵列孔径D下100次Monte Carlo试验后脉冲基线定位性能, 其中声源位于[x,y]=[0,40] m, CW脉冲频率为0.1fs, 阵列仍为置于x轴上以原点O为中心的ULA。随着阵列孔径的增大, 定位偏差不断减小。而随着阵元数的增加, 定向偏差变化不大, 测距偏差却在增大。

图6 不同阵元数与阵列孔径时脉冲基线定位性能示意图Fig. 6 Performance of pulse baseline positioning with different array number and array apertures

3 试验研究

为进一步实际检验脉冲基线定位性能, 在空气中模拟水下环境参数进行了 CW 脉冲定位试验。如图7所示, 采用2 m长10元ULA分别采集40.6 m外直线上5个位置点声源辐射的CW脉冲信号, 5 个声源位置的入射角分别为[–11.15°,–5.63°, 0°, 5.63°, 11.15°]。截取声源连续辐射的10个CW脉冲后, 图8中的方框给出了不同位置下这些CW脉冲的定位结果, 每个位置下的10个定位结果可以拟合得到1条直线, 5条直线大致交于坐标原点。从图中可知, 脉冲基线定位方法的测向结果较为稳定, 但测距结果波动较大。另外, 1 800 Hz和2 400 Hz CW 脉冲两侧位置的定位结果通常更加发散, 正对区域的定位结果相对更集中并接近真实位置, 这与仿真结论一致。

图7 空气中脉冲基线定位试验示意图Fig. 7 Experiment of pulse baseline positioning in air

图8 不同位置下多个CW脉冲的定位结果Fig. 8 Curves of positioning results with multiple CW pulse sources at different locations

4 结论

本文对近场条件下影响脉冲基线定位性能的各种因素进行了讨论, 以便根据不同实航环境选择合适的脉冲参数和阵列参数用于目标跟踪定位。仿真结果表明, 较高的采样频率或较低的脉冲频率有利于获得更高精度的脉冲前沿时刻估计,以提高脉冲基线方法的定位性能; 当声源位于阵列正对方向时, 脉冲基线定位方法性能略优, 且随着声源与阵列间距离的增大, 定向偏差大致保持不变, 而测距偏差则不断增大。阵列参数方面,随着阵列孔径的增大, 脉冲基线定位方法的定位性能不断改善, 而阵元数对其性能影响较小。

[1] Chen J C, Kung Y, Hudson R E. Source Localization and Beamforming[J]. IEEE Signal Processing Magazine, 2002, 19(2): 30-39.

[2] 宋新见. 数字式噪声目标被动测距声纳研究[D]. 哈尔滨:哈尔滨工程大学, 2004.

[3] 周伟. 三元阵浅海近程被动定位研究与分析[D]. 哈尔滨: 哈尔滨工程大学, 2009.

[4] Militello C, Buenafuente S R. An Exact Noniterative Linear Method for Locating Sources Based on Measuring Receiver Arrival Times[J]. Journal of the Acoustical Society of America, 2007, 121(6): 3595-3601.

[5] Smith J O, Abel J S. Clos ed-form Least-squares Source Location Estimation from Range-dif ference Measurements[J]. IEEE Transactions on Acoustics, Speech and Signal Processing, 1987, 35(12): 1661-1669.

[6] Schau H, Robinson A. Passive Source Localization Employing Intersecting Spherical Surfaces from T ime-ofarrival Differences[J]. IEEE Transactions on Acoustics, Speech and Signal Processing, 1987, 35(8): 1223-1225.

[7] 陈晓忠, 梁国龙, 王逸林, 等. 非同步水声定位技术及其性能评价[J]. 声学学报, 2003, 28(4): 357-362.

Chen Xiao-zhong, Liang Guo-long, Wang Yi-lin, et al. Nonsynchronous Underwater Acoustic Location and It′s Performance Evaluation[J]. Acta Acoustica, 2003, 28(4): 357-362.

[8] Yiteng H, Benesty J, Elko G W, et al. Real-time Passive Source Localization: a Practical Linear-correction Leastsquares Approach[J]. IEEE Transactions on Speech and Audio Processing, 2001, 9(8): 943-956.

[9] 罗丹. 噪声目标广义互相关被动测距研究[D]. 哈尔滨:哈尔滨工程大学, 2006.

[10] 黄翔东, 王兆华. 全相位FFT相位测量法的抗噪性能[J].数据采集与处理, 2011, 26(3): 286-291.

Huang Xiang-dong, Wang Zhao-hua. Anti-noise Performance of All-phase FFT Phase Measuring Method[J]. Journal of Data Acquisition & Processing, 2011, 26(3): 286-291.

[11] 陈奎孚, 王建立, 张森文. 频谱校正的复比值法[J]. 振动工程学报, 2008, 21(3): 314-318.

Chen Kui-fu, Wang Jian-li, Zhang Sen-wen. Spectrum Correction Based on the Complex Ratio of Discrete Spectrum Around the Main-lobe[J]. Journal of Vibration Engineering, 2008, 21(3): 314-318.

(责任编辑: 杨力军)

Influencing Factors of Pulse Baseline Positioning Performance in Near Field

DONG Li-ying, CHEN Zhi-fei
(School of Automation, Northwestern Polytechnical University, Xi′an 710072, China)

The equations of ranging and direction finding at the arrival time of leading pulse are deduced for pulse baseline positioning. The influences of the parameters of CW pulse, array, and sound source incident position on the performance of pulse baseline positioning are discussed. Simulation results show that the pulse baseline positioning can achieve better performance in the case of lower radiation frequency, larger array aperture, and the very source incidence against the array direction. Array number has little influence on the positioning performance, and with an increase in the range between sound source and array, the directional performance keeps stable, but the ranging performance decreases continuously.

pulse baseline positioning; near field; positioning performance

TJ630.6

A

1673-1948(2014)02-0100-05

2013-12-06;

2014-02-20.

中国博士后科学基金资助(2012M512027).

董利英(1981-), 女, 硕士, 主要研究方向为声学测量.