基于改进复合形法的成形磨齿工艺参数优化设计

张颂，赵大兴，丁国龙

(湖北工业大学机械工程学院，湖北武汉 430068)

姜彬等人［4］以车削时间、成本为目标函数，采用网格直接寻优方法对车削过程中的工艺参数进行了优化;王绍炘［5］以成本为目标函数，对滚齿工艺参数进行优化，优化的变量是滚刀速度和进给量;戴娟等人［6］以成本为目标函数，对外圆磨削工件速度、单位磨削宽度的金属切削率进行了优化;张慧鹏等［7］以效率为目标函数对无心磨削过程工艺参数进行了优化。他们的研究所建立的目标函数多以效率为准则，变量仅为一维或二维，没有考虑变量间相互影响，使用的方法需求导且效率较低，而且没有涉及到成形磨齿工艺参数优化。复合形法具有克服非线性、多极值等函数缺陷的优点。因此文中为实现高效高精加工齿轮，以成形磨齿利润率为目标函数，同时考虑磨齿机功率、刀具耐用度、磨削用量等条件的限制，提出基于改进复合形法［8］对成形磨齿工艺参数进行优化的方法，最终得到满足目标函数及约束条件的最优工艺参数。

1 成形磨齿工艺参数分析

在实际磨齿过程中，对于参数已定的单件齿轮，可以通过磨削用量的改变来提高磨齿加工效率、质量，降低加工时间、成本，最终使企业获得最高利益。砂轮速度越大，单位时间内磨粒磨削越快，同面积的磨削时间越短，效率越高。但过高砂轮速度使抛光作用减弱，因此在磨削低表面粗糙度时反而不如低速时的好，同时磨削热增加，机床震动增大，齿轮表面易出现烧伤、震纹、螺旋形波纹等缺陷。砂轮进给速度越大，接触时间缩短，效率提高，但是过高的进给速度会使磨削力增加，齿轮表面易烧伤，表面粗糙度易增大，太低则会影响磨齿效率。磨削深度越大，在磨削余量一定时，磨削次数相对减少，磨削时间减少，效率提高，但齿轮表面粗糙度值增加、砂轮磨损加剧，磨削力增加，易出现齿面烧伤，甚至破坏砂轮磨粒微刃。虽然砂轮速度、进给速度、磨削深度可以提高磨齿效率、表面质量，但是过高或过低的磨削用量都会有降低表面质量等缺陷，因此应根据实际限制条件选择合适的磨齿工艺参数，使在保证质量前提下提高效率、利润。

2 优化数学模型建立

2.1 变量设计

成形磨齿过程中磨削用量包括砂轮速度vs、进给速度f、磨削深度ap。单位分别为m/s，m/min，mm。磨削效率、成本、表面质量等与磨削用量有直接的关系，因此文中以砂轮速度、进给速度、磨削深度为设计变量。向量表示如下:

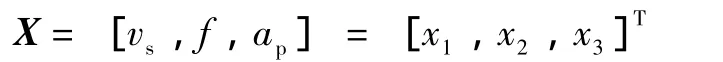
2.2 确定目标函数

提高利润率是企业生产经营最终目标。利润率的大小与时间、成本等有关，文中以成形磨齿利润率模型为目标函数，现对利润率进行分析。

单件齿轮磨削加工时间t包括基本时间tb、辅助时间ta、加工场所准备时间ts、休息时间tr、磨齿加工准备时间tp、砂轮修整时间td等。磨齿加工时间模型如下:

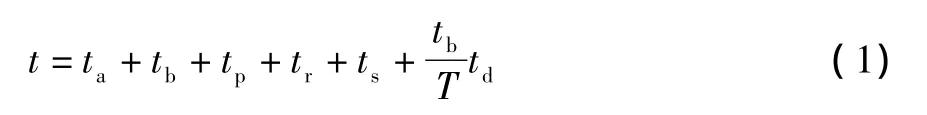
式中:T为砂轮耐用度。对于单件齿轮其ta、tp、tr、ts基本上是不变的，要提高磨齿效率，应尽量减小加工时间，而要减小加工时间只能通过tb来改变。基本磨削时间tb模型［9］如下:

式中:d为砂轮直径 (mm);z为齿轮齿数;b为磨削齿轮宽度 (mm);Z为磨齿轮余量 (mm)。根据著名的泰勒经验公式:

三是关于水功能区水质考核问题。对此项工作，省水利厅将按照2011年中央1号文件和国务院《关于实行最严格水资源管理制度的意见》要求，建立水功能区限制纳污制度。将积极与水利部和太湖流域管理局沟通衔接，确定好控制指标要求。同时将开展纳污总量管理，加快制定浙江省水功能区限制纳污指标体系和考核制度，促进包括太湖流域在内的全省水资源保护工作。目前，全省水功能区限制纳污指标分解和考核方案已完成初稿。强化入河排污口设置的审查管理，建立部门协作机制。进一步加强水资源监测能力建设，特别是加强《条例》确定的主要入太湖河道控制断面水资源监测能力建设，实行水功能区达标管理。

式中:Cr是常数;p，m，n为指数系数。

令:

把式 (2)— (4)代入式 (1)得:

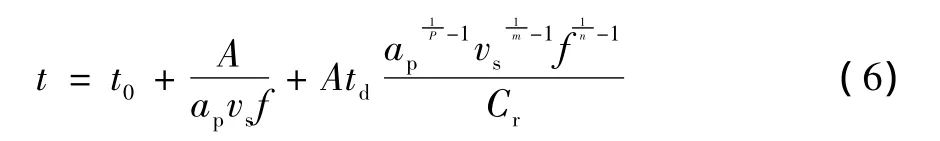
单件齿轮磨削成本C一般由齿轮材料费用、加工费用、砂轮及修整费用三大部分组成，成本数学模型如下:

式中:C0为单位时间磨削加工费用，Cw为单件齿轮材料费用，Cs为单位时间砂轮磨损费用。

式 (2)、(5)、(6)代入式 (7)得:

又利润率数学模型为:

其中:S为单件齿轮企业收取费用。将式 (6)、(8)代入式 (9)可得利润率最终表达式:

2.3 确定限制条件

(1)磨齿时要选取最佳的磨削用量，磨削深度、磨削进给量、磨削速度不能超过许可的范围:

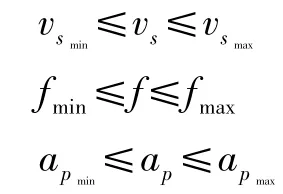
(2)为避免齿轮烧伤砂轮应具有一定耐用度:

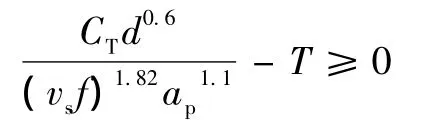
式中:CT为工件材料系数，对不用材料取值不同，一般未淬硬钢取2 550，淬硬钢取2 260;T为砂轮耐用度适用值，可按技术条件取。

(3)齿轮表面是否烧伤直接影响齿轮寿命、传动精度，也是评价齿轮好坏指标之一。因此对齿轮有防止烧伤的要求:

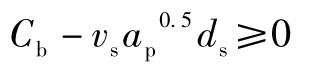
其中:Cb是磨削防止烧伤的临界系数，单位为m·mm/min，可以根据齿轮材料和砂轮的类型查表。

(4)磨齿时受到磨削力的作用，具有一定的负载功率，要求磨削功率满足在主轴功率的范围之内。即:

式中:ηc是机床主电机到主轴间传动效率，pc是主轴电机功率。

3 优化算法

优化问题分有约束和无约束两类。文中优化问题属于有约束优化问题，解决约束优化问题方法很多，常用的梯度搜索法及神经网络法等，逻辑结构复杂，而且有的运算量大，或者编程较难、效率低等。

该系统在MATLAB2009平台下，利用其编程简单、计算效率高等特点，通过建立利润率目标函数和约束条件，采用改进复合形法对齿轮磨削过程中磨削用量进行优化。求解出满足约束条件的砂轮速度、进给速度、磨削深度最优解，同时为了防止局部最优解的出现，采用随机比较算法的思想在得出前一个优化解后自动改变扩展系数α，再以此优化解作为初始点重新收索满足要求的最优解，当运行次数达到设定的值时结束，最后从优化解组中挑选出函数值最小的一组作为该模型的最优化解。实验结束后通过经验数据和图表来验证所得解为是否为最优。经过调用程序和计算，优化出砂轮速度、进给速度，磨削深度及目标函数值。计算程序框图如图1所示。

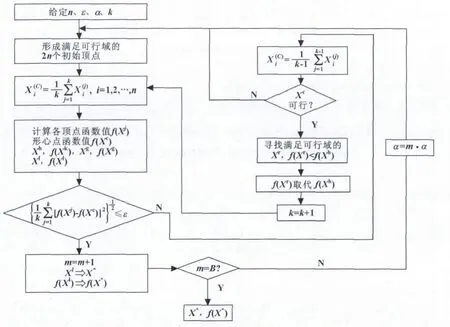
图1 复合形法流程

4 实例计算及分析

优化算例材料为淬火钢齿轮，选砂轮型号PSX200×20×32PA70 H8V35，成形磨齿机 YK7380为此次研究对象。取该工序收取费用S=55元;单位时间加工费用C0=1元;齿轮材料费用Cw=3元;其他磨削时间t0=3 min;砂轮磨损及修整费用Cs=1元;修整时间td=0.5 min。各约束条件及相关系数见表1。空间几何模型见图2，利润率与变量间关系如图3示。

表1 各系数取值

图2展示在以上条件下的利润率与砂轮速度、进给速度、磨削深度在空间上几何关系，图中磨削深度用颜色变化来表示;由图3知:利润率随着变量增大而增大，进给速度、砂轮速度越大利润率变化越慢、越平滑，但砂轮速度的影响较进给速度要大。经程序运行得:最佳砂轮速度32.70 m/s;进给速度7.34 mm/min;磨削深度0.041 mm;获得利润率为2.7元/min。

图2 函数的四维模型

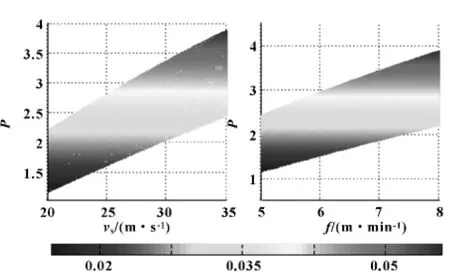
图3 利润率与变量变化关系

5 结束语

就成形磨齿工艺参数优化问题进行了相关的讨论，通过建立成形磨齿利润率数学模型和约束条件，用改进复合形法来解决成形磨齿参数优化问题，并给出了实际应用实例，通过实验验证此方法不仅简单易行，能够快速求解出最优解，且能够满足实际加工要求。利润率数学模型的建立同时考虑了磨齿效率和成本生产经营目标，具有利用单目标优化实现以往多目标优化的优点，同时避免建立多目标模型的环节。开发了一套成形磨齿参数优化系统，推荐出满足高效、低成本加工的参数，为企业获得最佳磨齿工艺参数提供了一种科学且有效的方法和一定的理论支撑。

［1］CHANG T C.工艺过程自动设计导论［M］.西安:西北工业大学出版社，1988.

［2］刘战强，艾兴.高速切削过程的优化［J］.机械设计与制造，2002(3):102－104.

［3］施志辉，刘杰.优化计算切削用量的实用方法［J］.工具技术，2008，42(1):86 －89.

［4］姜彬，郑敏利，李振加.数控车削的切削用量多目标优化［J］.哈尔滨理工大学学报，2001，6(2):43 －46.

［5］王绍炘.滚齿切削参数优化［J］.制造技术与机床，1994(8):20－22.

［6］戴娟，胡冠昱，高全芹.外圆磨磨削工艺参数的优化设计［J］.机械设计与制造，2008(8):131 －132.

［7］张慧鹏.基于MATLAB的无心磨削工艺参数优化［J］.组合机床与自动化加工技术，2009(10):85－87.

［8］梁尚明，殷国富.现代机械优化设计方法［M］.北京:化学工业出版社，2005.

［9］王先逵.机械制造工艺学［M］.北京:机械工业出版社，2007.

［10］王素粉.成形砂轮修整与齿轮磨削质量控制技术研究［D］.洛阳:河南科技大学，2010.

［11］LI G F，WANG L S，YANG L B.Multi-parameter Optimization and Control of the Cylindrical Grinding Process［M］.Journal of Materials Processing Technology，2002(11):232－236.