视觉传感网中基于二次规划的图像压缩感知
周钦青,陈遵德
视觉传感网中基于二次规划的图像压缩感知
周钦青,陈遵德
(顺德职业技术学院电子与信息工程系,广东 佛山 528333)
为降低视觉传感网络中图像压缩感知算法的计算复杂度,提出一种基于二次规划的网络图像恢复算法。该算法将压缩感知重构中的欠定线性方程组求解问题,转化为有界约束二次规划问题,在此基础上结合阿米霍步长准则,设计一种压缩感知图像恢复算法,通过求解二次规划问题对网络图像数据进行恢复。理论分析和仿真结果表明,与传统图像压缩感知算法相比,该算法可减少约1/3的图像数据恢复运算时间,且图像重构质量提高3 dB~6 dB,有效提高了视觉传感器网络图像恢复算法的实时性。
视觉传感网;压缩感知;图像恢复;二次规划;有界约束;实时性
1 概述
视觉传感网(Visual Sensor Networks, VSN)是由一组具有计算、存储和通信能力的视觉传感器设备组成的分布式感知网络,能够实时准确地从监测环境中获取含有特定事件信息的图像[1]。然而,视觉传感网将采集到的图像信息通过无线传输方式发送给使用者需要消耗大量能量,而节点携带电源能量却十分有限。因此,在保障监测质量的前提下降低网络图像数据传输能耗,延长节点寿命是视觉传感网技术迫切需要解决的问题[2]。
视觉传感网采集的图像数据具有很大的冗余性和相关性,减少冗余信息在网络中的传输是降低节点能耗的有效途径。作为一种利用信号稀疏性或可压缩性的全新信号采样理论,压缩感知(Compressed Sensing, CS)为实现这一目标提供了契机[3-4]。与分布式信源编码、图像编码等传统的图像数据压缩算法相比,基于压缩感知的图像数据恢复仅需在节点进行简单的测量运算,将复杂度较高的重构运算移至观测端,从而可进一步降低传感器节点的能耗负担。
然而,传统的基于压缩感知的图像恢复算法通常具有较高的计算复杂度,而视觉传感网对图像重建算法的实时性提出了高要求,因此,现有的图像压缩感知算法难以满足实时视觉传感网图像恢复要求。如在文献[5]中通过传统的线性规划(Linear Programming, LP)算法求解1范数最小化问题对视频数据进行重构。线性规划算法可得到较高的重构精度,但算法复杂度极高。文献[6-7]分别利用了匹配追踪算法(Matching Pursuit, MP)及迭代收缩算法[8](Iterative Shrinkage Threshold, IST),这2种算法可提高算法收敛速度,但重构精度不高。文献[9]的图像重构使用了压缩采样匹配追踪算法[10](Compressive Sampling Matching Pursuit, CoSaMP),该算法可达到与线性规划类似的重构精度,但对于视觉传感网中的海量图像数据而言,算法复杂度仍不能满足图像传输的高实时性要求。
针对目前视觉传感网图像恢复算法存在的不足,本文提出一种基于二次规划的网络图像数据恢复算法。与以往的算法不同,该算法将网络图像压缩感知中的欠定线性方程组求解问题转化为二次规划问题,同时结合阿米霍步长准则[11]设计一种网络数据恢复算法,通过求解二次规划问题对网络数据进行恢复。
2 问题描述
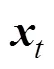

其中,向量表示的稀疏系数向量;表示向量的零范数,即向量中零元素的个数。
对图像数据进行稀疏变换后,可对图像数据进行测量,其过程可由下式表示:
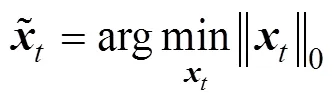
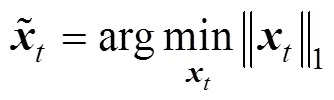
而本文将式(4)求解转化为二次规划问题,通过求解二次规划得到恢复图像。
3 网络图像数据的二次规划重构
3.1 算法描述



其中:
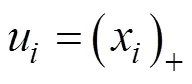

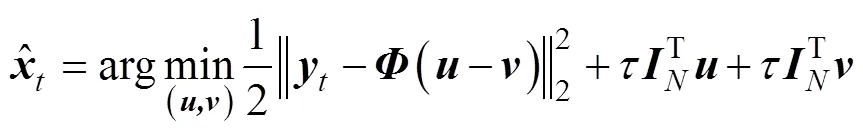

式(9)可写为二次规划的标准形式:

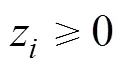




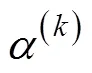


即:

在上述工作基础上,完整的算法步骤可整理为:
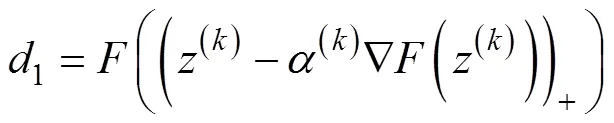
步骤5判断终止条件:

3.2 收敛性分析


结合式(16)可得:


综合式(17)、式(18)及文献[13]中定理2.4,即可得到算法的收敛性证明。
4 仿真实验结果
图2为在同一次重构中不同重构算法的重构图像与原始图像对比。其中,IST算法、CoSaMP算法、本文算法计算时间分别为:1.61 s、1.66 s、1.07 s;PSNR值分别为24.44 dB、26.95 dB、28.37 dB。

图2 重构图像与原始图像对比
由重构结果可以看出,本文算法可以达到较高的图像恢复质量,恢复的PSNR值略优于以往的压缩感知重构算法。同时,实验对算法计算时间的统计结果表明,对于同一分辨率的静态图像而言,本文算法计算时间相对经典恢复算法减少约1/3。实验在同一计算平台上进行,计算时间与算法复杂度呈正比,因此,以上结果也表明,本文算法的计算复杂度小于以往算法。

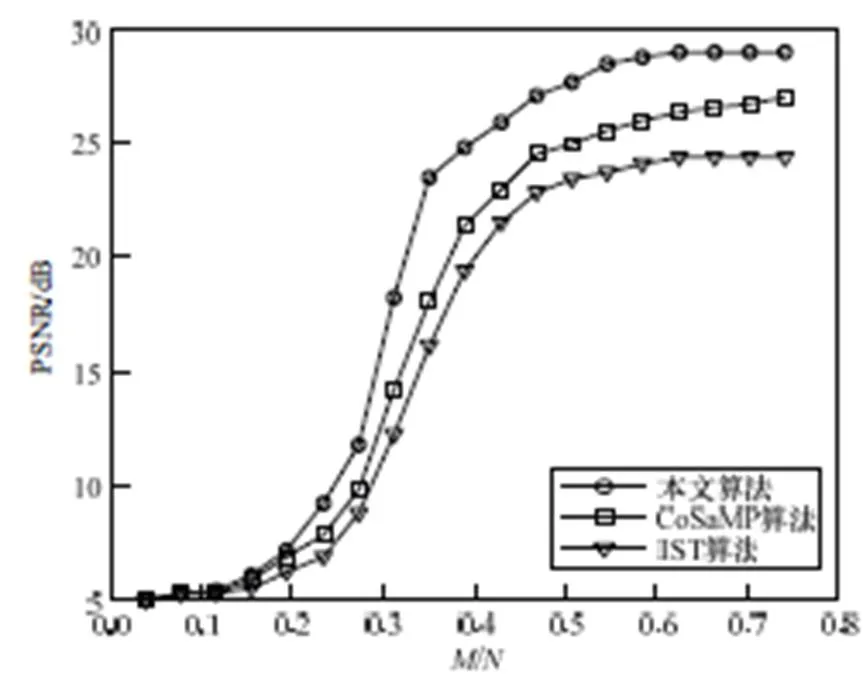
图3 网络数据重构质量对比

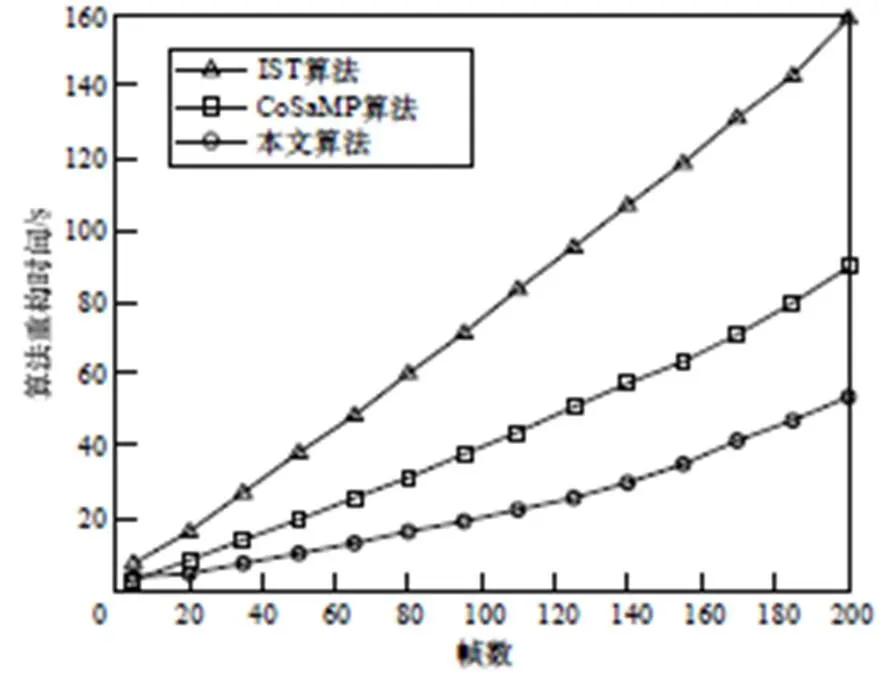
图4 不同算法重构时间对比
可以看出,本文算法计算时间小于IST算法及CoSaMP算法,并且随图像帧数的增加,算法优越性表现得越来越明显。图5所示的PSNR对比进一步验证了本文算法的有效性。

图5 不同算法重构质量对比
5 结束语
针对视觉传感网图像数据量大与传统压缩感知重构算法计算复杂度无法满足图像传输的高实时性问题,本文提出一种基于二次规划的网络图像恢复算法,该方法将压缩感知重构中的欠定线性方程组求解转换为二次规划问题。实验结果表明,相对于传统分布式压缩感知理论,本文算法可明显降低图像数据重构算法的计算复杂度,同时保证重构的准确度。对于网络图像数据而言,稀疏变换同样会对压缩感知重构的实时性造成影响,下一步将对此进行研究,并提出面向网络图像数据实时重构的稀疏变换方法。
[1] Misra S, Reisslein M, Xue Guoliang. A Survey of Multimedia Streaming in Wireless Sensor Networks[J]. IEEE Comm- unications Surveys and Tutorials, 2008, 10(4): 18-39.
[2] 马华东, 陶 丹. 多媒体传感器网络及其研究进展[J]. 软件学报, 2006, 17(9): 2013-2028.
[3] Donoho D. Compressed Sensing[J]. IEEE Trans. on Inform- ation Theory, 2006, 52(4): 1289-1306.
[4] 焦李成, 杨淑媛, 刘 芳, 等. 压缩感知回顾与展望[J]. 电子学报, 2011, 20(7): 1651-1662.
[5] Marcia R, Willet R. Compressive Coded Aperture Video Reconstruction[C]//Proc. of the 16th European Signal Processing Conference. Lausanne, Switzerland: European Association for Signal Processing, 2008: 3037-3041.
[6] Park J, Wakin M B. A Multiscale Framework for Compressive Sensing of Video[C]//Proc. of the 27th Conference on Picture Coding Symposium. Chicago, USA: [s. n.], 2009: 197-200.
[7] 练秋生, 肖 莹. 基于小波树结构和迭代收缩的图像压缩感知算法研究[J]. 电子与信息学报, 2011, 33(4): 967-971.
[8] Daubechies I, Defrise M, DeMol C. An Iterative Thresholding Algorithm for Linear Inverse Problems with a Sparsity Constraint[J]. Communications on Pure and Applied Mathematics, 2004, 57(11): 1413-1457.
[9] Sankaranarayanan A C, Turaga P, Baraniuk R, et al. Com- pressive Acquisition of Dynamic Scenes[C]//Proc. of the 11th European Conference on Computer Vision. Crete, Greece: [s. n.], 2010: 456-465.
[10] Needell D, Tropp J. Cosamp: Iterative Signal Recovery from Incomplete and Inaccurate Samples[J]. Applied and Computational Harmonic Analysis, 2009, 26(3): 301-321.
[11]Bertsekas D. Nonlinear Programming[M]. Boston, USA: [s. n.], 1999.
[12] Gan L, Do T, Tran T D. Fast Compressive Imaging Using Scrambled Hadamard Ensemble[C]//Proc. of the 16th European Signal Processing Conference. Lausanne, Switzerland: European Association for Signal Processing, 2008: 11-20.
[13] Birgin E G, Martnez J M, Raydan M. Nonmonotone Spectral Projected Gradient Methods on Convex Sets[J]. SIAM Journal on Optimization, 2000, 10(4): 1196-1211.
编辑 索书志
Image Compressed Sensing Based on Quadratic Programming in Visual Sensor Networks
ZHOU Qin-qing, CHEN Zun-de
(Department of Electronic and Information Engineering, Shunde Polytechnic College, Foshan 528333, China)
For reducing the computational complexity of Compressed Sensing(CS) in Visual Sensor Networks(VSN), an image recovery algorithm based on quadratic programming is proposed. The under-determined linear equations in CS recovery are solved by bound-constrained quadratic programming, and an image recovery algorithm is designed based on the armijo rule. Theory analysis and experimental results show that the proposed algorithm can reduce 1/3 operation time of image recovery, and enhance the recovery quality by 3 dB~6 dB, thus significantly improve the real-time performance of image recovery in VSN.
Visual Sensor Networks(VSN); Compressed Sensing(CS); image recovery; quadratic programming; bound-constrained; real-time performance
1000-3428(2014)03-0258-04
A
TP391.41
广东省信息技术教指委立项基金资助项目(XXJS-2013-35);顺德职业技术学院教改基金资助项目(2012-SZJGXM20)。
周钦青(1981-),女,讲师、硕士,主研方向:图像处理与分析,信息安全;陈遵德,教授、博士。
2013-01-16
2013-04-02 E-mail:sd22329975@126.com
10.3969/j.issn.1000-3428.2014.03.054

