航空遥感图像拼接算法及其精度评价

杨 彬，李旭东，晏 磊，余优生

航空遥感图像拼接算法及其精度评价

杨 彬1，李旭东2，晏 磊1，余优生3

(1. 北京大学遥感与地理信息系统研究所空间信息集成与3S工程应用北京市重点实验室，北京 100871； 2. 北京航空航天大学精密光机电一体化技术教育部重点实验室，北京 100191； 3. 北京星天地信息科技有限公司，北京 100083)

针对航空遥感成像范围小、视差角大的特点，提出一种航空遥感图像拼接算法。通过估算图像相对方位矩阵，使用透视变换实现图像校正，解决大视差角下的畸变问题。利用SIFT算法和基于概率密度的错误匹配点剔除方法，实现高精度图像配准，并通过小波变换完成图像融合工作。实验结果表明，在不同地表情况下，该算法的拼接性能均优于传统SIFT算法。

图像拼接；航空遥感；透视变换；小波变换；精度评价；图像校正

1 概述

航空遥感技术以其高空间分辨率、高时间分辨率、低成本及高安全性而越来越受到世界各国的重视。日本就使用航空遥感平台对核污染进行监测、对火山进行评估[1]；我国四川利用航空遥感影像进行灾区重建设计[2]。针对航空遥感技术获取数据的特点，探究航空遥感图像拼接算法及其相关精度评价是对两者综合应用的一种探索，具有积极意义。

图像拼接技术是近些年来图像处理领域发展迅速的研究方向之一。目前，图像拼接技术已经在图像压缩[3]、图像增强[4]、虚拟现实[5]等领域得到广泛应用。对于图像拼接技术，图像配准和图像融合是其2个重要组成部分。

目前，图像配准的方法很多，依据图像配准方法来分，主要集中在频率域和空间域2个部分[6]：(1)基于频率域一般利用傅里叶变换的相位相关性，这种方法一般对具有大尺度的旋转图像或者透视图像效果欠佳[7]；(2)空间域方法分为基于灰度的配准算法[8]和基于特征的配准算法，其中基于灰度的配准方法是比较基准图像与待配准图像相同尺寸灰度的差异[9]，而基于特征的匹配算法主要是通过特征提取和匹配来实现匹配，这种方法使用最多。

尺度不变特征变换(Scale Invariant Feature Transform, SIFT)算法是一种基于特征的配准方法，其自文献[10]提出后便被广泛应用于特征提取及相关领域中。文献[11]提出PCA-SIFT使用主成分分析法替换SIFT中的直方图方法；文献[12]提出SURF(Speeded Up Robust Features)对算法进行了提速。随着计算机技术的发展，SIFT算法以及其衍生算法(PCA-SIFT，SURF)得到越来越广泛的应用。

图像融合技术是将多幅影像或者多种特征结合为一幅影像的过程[13]。简单的方法有光强平均融合、加权平均融合、中值滤波法等，复杂的有高斯样条插值法、小波变换[14]等。前者具有处理数据量小、速度快等特点，但是在复杂场景下难以满足融合要求；复杂的方法精度较高，但是处理数据量大，速度较慢。近年来，小波变换在图像处理领域得到广泛应用，其在图像融合领域中也发挥着越来越大的作用。本文提出一种新的航空遥感图像数据拼接算法，并对其精度评价方法进行研究。

2 基于透视变换的图像校正方法

透视变换可以看成是一种特定的单应性变换，可以将同一个三维物体分别投影到2个不同投影平面下的2幅图像联系起来。本文选定左图像所在的像空间辅助坐标系(像主点为原点)为基准坐标系，将右图像所在的像空间辅助坐标系(像主点为原点)转换到这个基准坐标系中，如图1所示。

图1 透视变换图像校正示意图

当对具有较大视差角的2幅图像拼接时，匹配点会大量集中于特征明显的几个区域，少量高精度的匹配点出现在这几个区域之外，从而导致RANSAC等算法估算2幅图像的相对方位元素时造成较大误差(在大视差角下更为明显)，而使用上述算法首先通过人工选取同名像点的方法进行粗配准，而后使用SIFT算法进行高精度配准，能够减少误差，且这种处理方法的效果和具有高精度外方位元素的配准是一致的[15]。

3 基于SIFT算法的特征提取及匹配方法

SIFT算法提取的特征是图像的局部特征，其对旋转、尺度缩放、亮度变换保持不变性，能够在海量特征数据库中进行快速、准确的配准。SIFT算法使用了128维描述符描述。但是实验结果仍存在错误匹配点。为了进一步提高匹配精度，本文研究了一种基于概率密度的错误匹配点剔除方法，实验证明该方法对于经过透视变换的航空遥感图像有很好的作用，能够有效地剔除错误的匹配点。

假设航空遥感平台上的相机在获取了一个房子的图像，以左图像为基准，对右图像进行透视变换，则房子在右图像中的位置及姿态应与左图像保持一致。假设最终有4对特征点匹配成功并且其匹配效果如图2所示。从中可以看出，有3对特征点匹配成功(实线所示)，1对特征点匹配错误(虚线所示)。

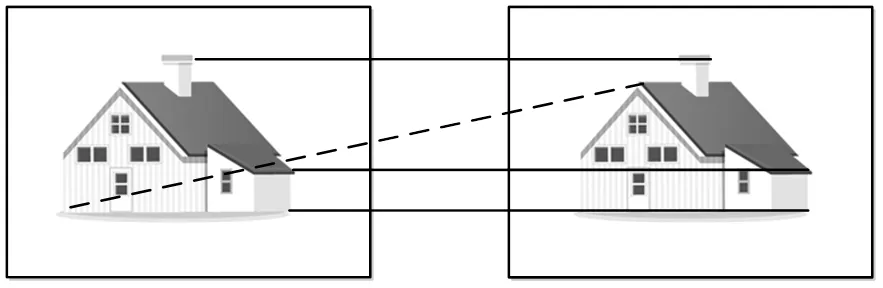
图2 错误匹配情况

由于图像是经过透视变换的，因此如果1对匹配点是正确的匹配关系，那么其连线的斜率应该为零或近似为0，若出现明显不为0或超出一定斜率界限的匹配点，则可以判定匹配精度较低甚至错误。

4 精度评价方法

在图像融合时，本文中采用均值融合规则对低频分量进行融合，最大值融合规则对高频分量进行融合。

对于一幅×的图像而言，融合后图像与原始图像的均方根误差定义为：

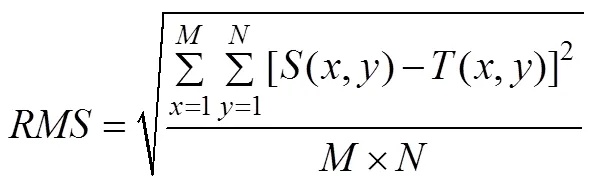
5 实验测试与分析

本文实验主要分为2个部分：(1)探究小波构建层数对融合效果影响，确定符合航空遥感影像的最佳构建层数；(2)2种不同场景的图像拼接实验，证明本文方法的有效性。本文中使用的航空遥感影像不包含任何姿态和位置信息。

5.1 提升小波构建层数对融合效果的影响

实验首先对源图像A进行不同部分的图像模糊形成图像B和C。然后将它们使用不同的小波构建层数进行图像融合，最后比较融合耗时及精度，如图3所示。

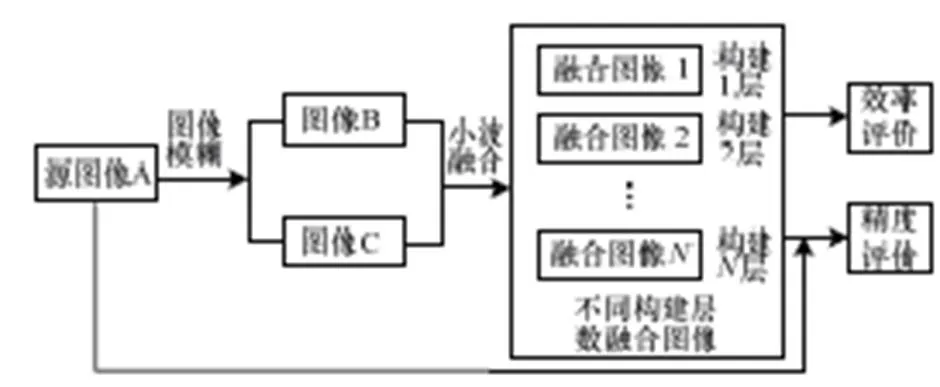
图3 构建层数对小波融合影响的研究方案

5.1.1 效率评价

采用9×9的平均模糊模板对图像进行左模糊、右模糊(即平均模糊作用的图像区域分别为左侧、右侧)，实验原始图及模糊效果如图4所示。

图4 模糊处理效果

源图像大小为512×512像素，通过构建1层~7层小波，每层小波运算10次，取平均耗时作为该层耗时，可以比较得到效率与构建层数的关系，如图5所示。可以看出，构建不同层数的小波对融合时间并没有太大的影响，算法运行时间在1.5 s~2.3 s之间稳定浮动。经过分析，是由源图像较小，且提升小波变换在每多构建一层小波时，多增加的数据处理量会随2的指数次幂减少引起的。

图5 9×9模板模糊的效率分析

5.1.2 精度评价

在初始条件下，方差随着构建层数的增加而减少，即构建层数越多，精度越高。但当构建层数达到4层后，精度保持不变，如图6所示。

图6 9×9模板模糊的精度分析

5.1.3 图像融合

基于以上效率与精度分析，本文通过构建4层小波来实现9×9模板模糊的图像融合，效果如图7所示。可以看出融合效果很好，融合方差为1.49。

图7 9×9模板融合效果

5.1.4 不同模版的模糊实验

依据图3所述方法，分别实施模版为3×3、5×5、7×7的实验，可以得到类似结果。从图8~图10可以看出，虽然模糊程度不断增加，但是在提升小波变换时，耗时基本保持不变。在精度方面，随着模糊程度的增加，需要构建的小波层数会增加，但是增加速度缓慢，在9×9模糊时，也只需要构建4层提升小波即可。基于以上结果，本文中实验采用构建2层小波的方法来实现图像的融合。

图8 3×3模板模糊效率与精度分析

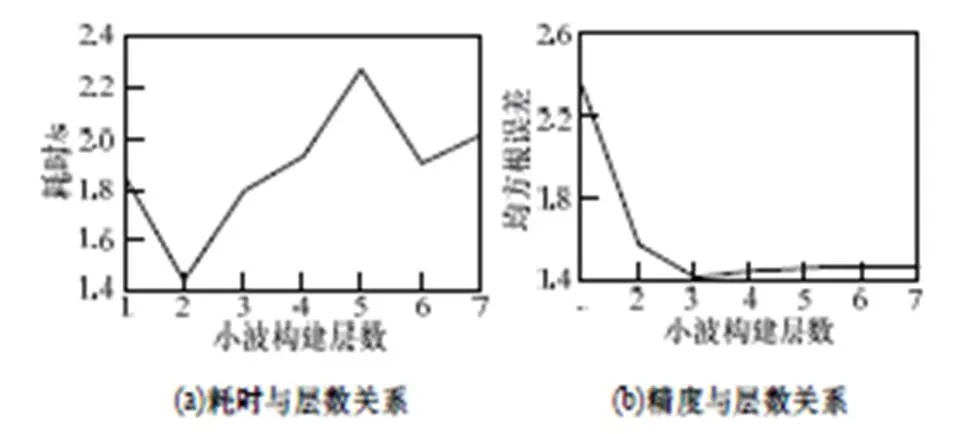
图9 5×5模板模糊效率与精度分析

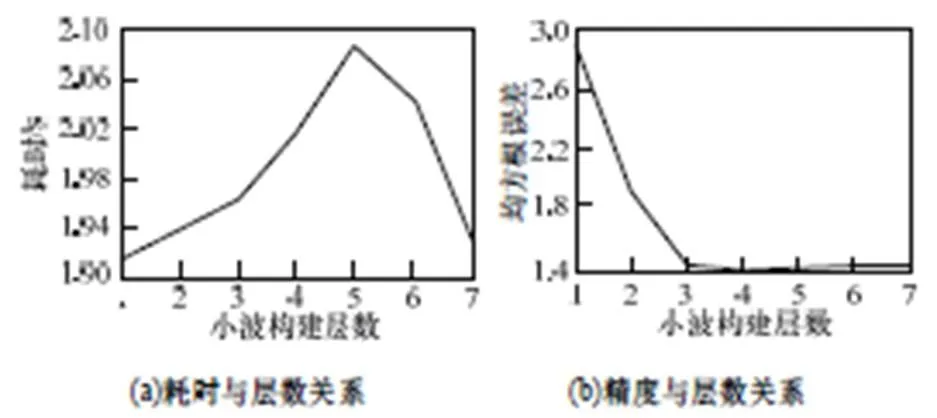
图10 7×7模板模糊效率与精度分析

5.2 拼接实验

拼接精度评价方法可以从2个层面展开：(1)肉眼观测，若是存在肉眼可见的拼接误差，如重影、接边线等，则可判定拼接失败，无需进行定量上的评价；(2)若无肉眼可观测拼接误差，则通过均方根误差评价。

5.2.1 场景1实验

在场景1中，左图像如图11所示，右图像如图12所示，传统SIFT拼接方法(没有经过透视变换预处理)图像拼接图如图13所示，采用本文方法图像拼接图如图14所示。

图11 场景1左图像

图12 场景1右图像

图13 传统SIFT方法的图像拼接图(场景1)

图14 本文方法的图像拼接图(场景1)

对比图13和图14可以看出，未采用透视变换的图像拼接图会出现重影，尤其是图12中的方框部分，田间的小道以及凸起部分都有不同程度的重影，拼接图与原始图像的左图与右图存在偏差，拼接结果较差。采用透视变的图像拼接结果很好，拼接图与原始图像的左图与右图偏差较小，符合图像拼接的要求。

5.2.2 场景2实验

在场景2中，左图像如图15所示，右图像如图16所示，传统SIFT拼接方法(没有经过透视变换预处理)图像拼接图如图17所示，采用本文方法的图像拼接图如图18所示。

图15 场景2左图像

图16 场景2右图像

图17 传统SIFT方法的图像拼接图(场景2)

图18 本文方法的图像拼接图(场景2)

对比图17与图18，从肉眼上来看细节部分类似，不能判别出较大差异。通过对其精度进行计算，图17未采用透视变换的图像拼接图方差为2.69，而图18中本文方法的图像拼接图方差为1.85，采用透视变换的方差相比未采用透视变换的方差要小，因而采用透视变换的拼接图更接近真实情景，更符合拼接的要求。

6 结束语

本文是对航空遥感图像数据拼接进行探索，为提高拼接的精度，提出了基于透视变换的图像校正、基于SIFT算法的特征提取及匹配、基于提升小波变换的图像融合以及精度评价方法相结合图像拼接算法，实验结果证明该算法可行、有效，与传统SIFT算法相比具有更高的稳定性及实验结果具有更高的真实性。下一步将对图像校正、配准和精度评价方法进行优化，以进一步提高算法时效性，减少存储容量和计算量。

[1] 鲁云飞. 无人机遥感图像自动配准技术研究[D]. 北京: 北京大学, 2011.

[2] 鲁 恒, 李永树, 李何超, 等. 无人机影像数字处理及在地震灾区重建中的应用[J]. 西南交通大学学报, 2008, 45(4): 533-538.

[3] Frederic D, Janusz K. Efficient, Robust, and Fast Global Motion Estimation for Video Coding[J].IEEE Transactions on Image Processing, 2000, 9(3): 497-501.

[4] Michal I, Shmuel P. Motion Analysis for Image Enhancement: Resolution, Occlusion and Transparency[J]. Journal of Visual Communication and Image Representation, 1993, 4(4): 324- 335.

[5] Szeliski R, Shum H Y. Creating Full View Panoramic Image Mosaics and Environment Maps[C]//Proc. of SIGGRAPG’97. Los Angeles, USA: [s. n.], 1997.

[6] 狄颖辰, 陈云坪, 陈莹莹, 等. 无人机图像拼接算法综述[J].

计算机应用, 2011, 31(1): 170-174.

[7] Pan Wei, Qin Kaihuai, Chen Yao. An Adaptable-Multilayer Fractional Fourier Transform Approach for Image Regis- tration[J].IEEE Transactions on Pattern Analysis and Machine Intelligence, 2009, 31(3): 400-413.

[8] 王 斌, 王伟锋. 一种基于局部灰度匹配的无人机图像拼接算法[J]. 中国石油大学学报, 2009, 33(6): 38-42.

[9] Yang Guosheng, Zhang Huanlong, Yang Yulin. Study of Image Mosaic Based on the Method of Finite Difference[C]//Proc. of 2008 Congress on Image and Signal Processing. Sanya, China: [s. n.], 2008.

[10] David G L. Distinctive Image Features from Scale-Invariant Keypoints[J].International Journal of Computer Vision, 2004, 60(2): 91-110.

[11] Yan Ke, Rahul S. PCA-SIFT: A More Distinctive Represen- tation for Local Image Descriptors[J].Computer Vision and Pattern Recognition, 2004, 60(2): 506-513.

[12] Herbert B, Andreas E, Tinne T, et al. SURF: Speeded-Up Robust Features[J]. Computer Vision and Image Understanding, 2008, 110(3): 346-359.

[13] John J L, Robert J, Stavri G N, et al. Pixel- and Region-based Image Fusion with Complex Wavelets[J]. Information Fusion, 2007, 8(2): 119-130.

[14] Li Shutao, James T K, Wang Yaonan. Using the Discrete Wavelet Frame Transform to Merge Landsat TM and Spot Panchromatic Images[J].Information Fusion, 2002, 3(1): 17-23.

[15] 朱述龙, 黄晓波, 陈 虹, 等. 大倾斜面阵CCD图像的几何校正[J]. 解放军测绘学院学报, 1999, 16(2): 113-115.

编辑 金胡考

Mosaic Algorithm for Aerial Remote Sensing Image and Its Accuracy Evaluation

YANG Bin1, LI Xu-dong2, YAN Lei1, YU You-sheng3

(1. Beijing KeyLab of Spatial Information Integration & Its 3S Engineering Applications, Institute of Remote Sensing & Geographic Information System, Peking University, Beijing 100871, China; 2. Key Laboratory of Precision Opto-mechatronics Technology, Ministry of Education, Beihang University, Beijing 100191, China; 3. Beijing XTD Information & Technology Co., Ltd., Beijing 100083, China)

Small imaging coverage and big parallax angle make aerial remote sensing more difficult to image processing. This paper proposes an algorithm for aerial remote sensing image mosaic. The original image is corrected by perspective transform with estimating matrix which is determined by the relative attitude of two images. It solves the distortion problem caused by big parallax angle. Image registration is approached by the Scale Invariant Feature Transform(SIFT) algorithm and a method based on probability density. The image mosaic process is completed by the wavelet transform. Experimental result shows that the mosaic performance of this algorithm is better than traditional SIFT algorithm in different surface conditions.

image mosaic; aerial remote sensing; perspective transform; wavelet transform; accuracy evaluation; image correction

1000-3428(2014)03-0253-05

A

TP911.73

国家自然科学基金资助项目“内视场拼接相机的数字基高比模型与精度评价机理”(11174017)；国家科技支撑计划基金资助项目“大规模航空遥感产业化综合应用示范”(2011BAH12B07)。

杨 彬(1989－)，男，博士研究生，主研方向：摄影测量与遥感；李旭东，副教授、博士；晏 磊，教授、博士；余优生，工程师。

2012-10-11

2012-12-28 E-mail：ybjason89@163.com

10.3969/j.issn.1000-3428.2014.03.053