简化轮LBlock的密钥中比特检测及分析

莫 钊，韦永壮



简化轮LBlock的密钥中比特检测及分析

莫 钊，韦永壮

(桂林电子科技大学广西信息科学实验中心，广西 桂林 541004)

LBlock密码算法是近来提出的一类轻量级分组加密算法。利用LBlock算法的结构特点，结合立方检测的基本思想，设计2个密钥中比特捕获算法，对LBlock算法输出所涉及的密钥比特个数情况进行分析。9轮简化LBlock的每个输出比特全部卷入所有的主密钥比特信息，在18维立方变元下，11轮简化LBlock的输出累加中每个比特全部卷入所有的主密钥比特信息。上述2轮简化LBlock均不存在密钥中比特。研究结果表明，全轮LBlock密码算法具有稳固的密钥信息扩散及混淆性，足以抵抗经典立方攻击。

轻量级密码；分组密码；密钥中比特；立方测试；盒；LBlock密码

1 概述

射频识别(Radio Frequency Identification, RFID)[1]技术与无线传感器网络[2]的资源(包括计算和处理能力、能量资源、存储空间和通信带宽等)非常有限，大大限制了各种传统密码算法的使用。如何确保射频识别无线传感器网络的安全可靠性成为业界的瓶颈问题。在构建安全的射频识别和无线传感器网络中，轻量级的密码技术[3](即在确保算法足够安全性的前提下，功耗、计算及存储资源等开销较少、实现速度轻便的密码)成为当前研究的热点。轻量级分组密码具有算法加解密速度快、容易标准化、便于软硬件实现等优点。目前，轻量级分组密码在RFID安全和无线传感器网络中发挥着重要的作用。

近几年出现一系列轻量分组密码算法，如：TEA[4]，KTANTAN[5]，HIGHT[6]，MIBS[7]，mCrypton[8]等。特别值得关注的是，在2011年国内学者提出了一种新的轻量级分组密码LBlock(鲁班锁)[9]。LBlock的分组长度为64比特，密钥长度为80比特(共有32轮)。由于其结构简洁、紧凑，在软、硬件环境中高效实现，特别适合受限环境下使用等优点，因此受到业内广泛的关注。

文献[10]通过分析LBlock密钥编排存在的缺陷，以时间复杂度为270和数据复杂度为247的明文对，给出第22轮LBlock相关密钥不可能差分攻击。文献[11]从设计者算法评估分析结果中，将LBlock攻击轮数提高至第21轮和 第22轮，攻击的复杂度分别可达269.5及279.28。文献[12]对第16轮LBlock构建一种相关密钥的飞去来器差分攻击。其次，基于上面第16轮相关密钥的截断差分，对第22轮LBlock实施密钥恢复攻击，与之前其他人的攻击结果对比，数据复杂度和计算复杂度均有提高。文献[13]以262.5选择明文对的数据复杂度和273.7的时间复杂度，对第21轮LBlock加密进行了不可能差分攻击。文献[14]基于矩阵分析的方法，得到第14轮LBlock区分器，并提出了第22轮LBlock的零相关线性攻击。攻击的数据复杂度和时间复杂度分别可达262.1和271.27。文献[15]分析了LBlock算法的安全强度，指出基于2种独立密钥差分路径的Biclique分析，结合不完全匹配和预计算技术，对全轮(32轮)LBlock进行密钥恢复攻击。攻击的数据复杂度不超过252个选择明文，还有时间复杂度是278.4左右。文献[16]对LBlock进行了侧信道立方攻击。结果显示，结合第3轮LBlock比特输出的密钥扩散分析，在单比特泄露模型下通过捕获第3轮的第44个状态比特，以210.7时间复杂度和27.6个选择明文，至少可以恢复14个比特密钥。而在汉明重量泄露模型下，以误差允许概率为5.52%，数据复杂度为230和28.5个选择明文，得到第32轮LBlock的80比特密钥。

上述的攻击方法大都是从LBlock算法的“整体结构”来研究算法的安全性(尽管文献[17]研究了低轮LBlock算法的代数次数)，如何从算法“局部”把握算法的安全性，如算法局部密钥信息扩散及混淆性程度(如密钥中比特)问题等亟待解决。

另一方面，由于立方攻击实现的条件比较简洁，且应用范围广泛，对多种密码的分析(如Trivium[18-19]、Grain- 128[20]、MD6[18]、Hitag2[21]等)取得良好的效果。特别地，Hitag2是一种应用于远程控制小车门锁的轻量级密码；文献[22]对Hitag2实施了立方攻击。实验结果表明，在PC机上仅需1 min便可完全破解Hitag2。可见立方攻击对轻量级流密码可产生实际威胁。那么一个重要的问题是：新型的轻量级分组密码算法LBlock是否足以抵抗立方攻击，这仍有待深入研究。

本文基于LBlock算法的结构特点，结合立方检测(Cube testers)[18]的基本思想，设计2个密钥中比特捕获算法。算法1检测了2轮~9轮简化LBlock算法的密钥信息扩散及混淆性。算法2检测了在18维立方变元下，2轮~11轮简化LBlock算法的密钥信息扩散及混淆性，并进一步分析了LBlock算法抵抗立方测试攻击的能力。

2 立方测试的基本思想

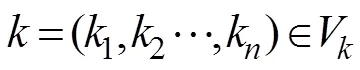
例假设6个比特的输入加密函数：

立方密钥中比特检测算法步骤如下：

第1步

第2步

(3)最终输出所有的密钥中比特。

如果密码算法存在密钥中比特，则说明此密钥比特并没有对密文输出产生任何影响，因而其密钥信息扩散性并不好。根据密码算法扩散原则，即算法的每个明文比特和密钥比特都要对密文产生影响。密钥中比特检测的目的就是分析密文输出中所涉及的密钥比特个数，以便检验和评判密钥信息在算法内部状态中扩散的程度。

3 LBlock的算法描述

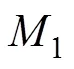
图1 LBlock加密流程

(1)LBlock的数据处理过程如下：

(2)轮函数的执行过程：

：(2)64→(2)64

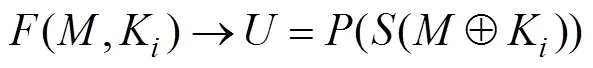
其中，代表轮函数的输出；和分别表示混淆函数和扩散函数，后面给出和的定义。

(3)混淆函数的定义：

混淆函数的输入输出均为32比特。混淆函数代表轮函数的非线性层，由8个盒01234567并行组成。每个盒的输入输出均为4个比特。其中，LBlock 的8个盒的数据如表1所示。

表1 LBlock的S盒

：(2)32→(2)32

=7‖6‖5‖4‖3‖2‖1‖0→

=7‖6‖5‖4‖3‖2‖1‖0

(4)扩散函数的定义：

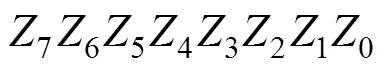
:(2)32→(2)32

=7‖6‖5‖4‖3‖2‖1‖0→

=7‖6‖5‖4‖3‖2‖1‖0

, , ,

由于篇幅有限，密钥编排可参见文献[9]。

4 S盒的布尔函数表达式

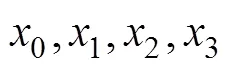
5 2轮~9轮LBlock的密钥中比特检测

性质1 简化LBlock算法至少需要迭代9轮，才足以保证其输出位涉入全部密钥比特。

第3步最终输出所有的密钥中比特。

在配置为Intel Core i7-2600 3.40 GHz，4 GB DDR3的PC机上，利用软件Visual C++ 6.0进行C语言编程测试(后面进行的测试以同样的配置)。

通过搜索发现：

第2、3轮LBlock的第1个输出位其中比特、布尔表达式及最高代数次数如下：

第2轮：

中比特：022,2759,6479

中比特个数：72

代数表达式：2425266123252425236123622461256023632462246325636061606260636163626323606223616224606225606124616225606225606325616360626325606263

最高代数次数：4

第3轮：

中比特：030,3555,6063,6873,78,79

中比特个数：64

最高代数次数：6

代数表达式：(在此省略)。

第4轮~第9轮LBlock的第1个输出位其中特如下：

第4轮：

中比特：0,1,626,3134,3942,5267,7679

中比特个数：51

第5轮：

中比特：25,1013,2338,4751,5759,7275

中比特个数：36

第6轮：

中比特：09,1822,28,29,30,4346,64

中比特个数：23

第7轮：

中比特：011415161735

中比特个数：7

第8轮：

中比特：6

中比特个数：1

第9轮：

中比特：无

中比特个数：0

从以上结果看出：LBlock第2、3轮输出表达式所涉及的密钥分别只有8个和16个；类似地，同样发现其他输出位存在类似的结果(密钥中比特检测失败概率为2–30)。

6 8轮~11轮LBlock的立方密钥中比特检测

性质2 在18维立方变元测试下，简化LBlock算法至少需要迭代11轮，才能保证其输出位涉入全部密钥比特。

最终输出所有的密钥中比特。

对LBlock算法输出第13位进行检测结果如下：

第8轮：

中比特：0~79

中比特个数：80

第9轮：

中比特：78,79

中比特个数：2

第10轮：

中比特：28

中比特个数：1

第11轮：

中比特：没有

中比特个数：0

类似地，改变立方变元位置和函数输出位置，对LBlock进行立方中比特检测，结果见表2。

由表2看出：LBlock第8轮~第10轮输出表达式中 (第13位)仍存在中比特。在18个立方变元下LBlock至少需要迭代11轮，才足以保证其第13个输出位涉入全部密钥比特。类似地，把立方变元提高到23个比特时，多次的测试结果仍表明11轮变换下不存在密钥中比特，并且这些密钥信息是以非线性形式存在的，包括测试其他输出比特(密钥中比特检测失败概率为2–30)。

表2 立方中比特的检测

注意到，全轮LBlock采用32次轮函数迭代，因此，该算法具有稳固的密钥信息扩散及混淆性以抵抗立方密钥中比特测试。

7 结束语

分组密码输出位的密钥中比特数量是度量算法安全强度的一个重要参数。若某一输出位含有多个密钥中比特信息，则被认为算法的扩散及混淆程度不足。本文利用立方测试基本思想，结合密钥中比特算法，检测了LBlock加密算法输出位密钥比特的分布情况。2种测试结果表明，全轮 (32轮)LBlock算法具有理想的密钥信息扩散及混淆性。下一步将通过密钥中比特检测技术减小具体攻击中的时间复杂度。

[1] Finkenzeller K. RFID Handbook: Fundamentals and Applica- tions in Contactless Smart Cards and Identifiaction[M]. Chichester, UK: John Wiley, 2003.

[2] Akyildiz I F, Su Weilian, Sankarasubramaniam Y, et al. A Survey on Sensor Networks[J]. IEEE Communications Magazine, 2002, 40(8): 102-114.

[3] Bogdanov A, Knudsen L R, Leander G, et al. Present: An Ultra-lightweight Block Cipher[C]//Proceedings of the 9th Inter- national Workshop on Cryptographic Hardware and Embedded Systems. Berlin, Germany: Springer-Verlag, 2007: 450-466.

[4] Wheeler D, Needham R. A Tiny Encryption Algorithm[C]// Proceedings of the 2nd International Workshop on Fast Software Encryption. Berlin, Germany: Springer-Verlag, 1994: 363- 366.

[5] Cannière C D, Dunkelman O, Knežević M. KATAN and KTANTAN——A Family of Small and Efficient Hardware- oriented Block Ciphers[C]//Proceedings of the 11th International Workshop on Cryptographic Hardware and Embedded Systems.Berlin, Germany: Springer-Verlag, 2009: 272-288.

[6] Hong D, Sung J, Hong S, et al. HIGHT: A New Block Cipher Suitable for Low-resource Device[C]//Proceedings of the 8th International Workshop on Cryptographic Hardware and Embedded Systems. Berlin, Germany: Springer-Verlag, 2006: 46-59.

[7] Izadi M, Sadeghiyan B, Sadeghian S, et al. MIBS: A New Lightweight Block Cipher[C]//Proceedings of the 8th International Conference on Cryptology and Network Security. Berlin, Germany: Springer-Verlag, 2009: 334-348.

[8] Lim C, Korkish O. MCrypton——A Lightweight Block Cipher for Security of Low-cost RFID Tags and Sensors[C]// Proceedings of the 6th International Workshop on Information Security Applications. Berlin, Germany: Springer-Verlag, 2005: 243-258.

[9] Wu Wenling, Zhang Lei. LBlock: A Lightweight Block Ci- pher[C]//Proceedings of the 9th International Conference on Applied Cryptography and Network Security. Berlin, Germany: Springer-Verlag, 2011: 327-344.

[10] Minier M, Naya-Plasencia M. A Related Key Impossible Differential Attack Against 22 Rounds of the Lightweight Block Cipher LBlock[J]. Elsevier Information Processing Letters, 2012, 112(1): 624-629.

[11] KarakocF, Demirci H, HarmancıA E. Impossible Differential Cryptanalysis of Reduced-round LBlock[C]//Proceedings of the 6th IFIP WG11.2 International Workshop on Information Security Theory and Practice. Berlin, Germany: Springer-Verlag, 2012: 179-188.

[12] Liu Shusheng, Gong Zheng, Wang Libin. Improved Related Key Differential Attacks on Reduced-round LBlock[C]//Proceedings of the 14th International Conference on Information and Communications Security. Berlin, Germany: Springer-Verlag, 2012: 58-69.

[13] Liu Ya, Gu Dawu, Liu Zhiqiang, et al. Impossible Differential Attacks on Reduced-round LBlock[C]//Proceedings of the 8th International Conference on Information Security Practice and Experience. Berlin, Germany: Springer-Verlag, 2012: 97-108.

[14] SoleimanyH, Nyberg K. Zero-correlation Linear Cryptan- alaysis of Reduced-round LBlock[DB/OL]. (2012-10-05). http://eprint.i-acr. org/2012/570.pdf.

[15] Wang Yanfeng, Wu Wenling, Yu Xiaoli, et al. Security on LBlock Against Biclique Cryptanalysis[C]//Proceedings. of the 13th International Workshop on Information Security Applications. Berlin, Germany: Springer-Verlag, 2012: 1-14.

[16]Li Zhenqi, Zhang Bin, Yao Yuan, et al. Cube Cryptanalysis of LBlock with Noisy Leakage[C]//Proceedings of the 15th International Conference on Information Securityand Cryptology. Berlin, Germany: Springer-Verlag, 2012: 141-155.

[17] 彭昌勇, 祝跃飞, 顾纯祥, 等. 1~5轮LBlock 的多项式表示及完全性分析[J]. 计算机工程, 2012, 38(9): 155-157, 179.

[18] AumassonJ P, Dinur I, Meier W, et al. Cube Testers and Key Recovery Attacks on Reduced-round MD6 and Trivium[C]// Proceedings of the 16th International Workshop on Fast Software Encryption. Berlin, Germany: Springer-Verlag, 2012: 1-22.

[19] Piotr M, Janusz S. The Cube Attackon Stream Cipher Trivium and Quadraticity Tests[EB/OL]. (2011-01-18). http://eprint.iacr. org/2011/032.pdf.

[20] AumassonJ P, Dinur I, Meier W, et al. Efficient FPGA Implements of High-dimensional Cube Testers on the Stream Cipher Grain-128[C]//Proceedings of IACR’09. [S. 1.]: IEEE Press, 2009: 218-230.

[21]Wiener I. Hitag2 Specification, Reference Implementation and Test Vectors[EB/OL]. (2011-05-13). http://cryptolib.com/cip hers/hitag2.

[22] Sun Siwei, Hu Lei, Xie Yonghong, et al. Cube Crypt-analysis of Hitag2 Stream Cipher[C]//Proceedings of the 10thInternational Conference on Cryptology and Network Security. Berlin, Germany: Springer-Verlag, 2011: 15-25.

[23] DinurI, Shamir A. Cube Attacks on Tweakable Black Box Polynomials[C]//Proceedings of the 28th Annual International Conference on the Theory and Applications of Cryptographic Techniques. Berlin, Germany: Springer-Verlag, 2009: 278- 299.

[24] DinurI, Shamir A. Applying Cube Attacks to Stream Ciphers in Realistic Scenarios[J]. Cryptography and Communications, 2012, 4(3/4): 217-232.

[25] Dinur, Shamir A. Side Channel Cube Attacks on Block Ciphers[DB/OL]. (2009-05-18). http://eprint.iacr.org/2009/127. pdf.

编辑 索书志

Detection and Analysis of Key Neutral-bit for Reduced Round LBlock

MO Zhao, WEI Yong-zhuang

(Guangxi Experiment Center of Information Science, Guilin University of Electronic Technology, Guilin 541004, China)

Recently, LBlock as a new lightweight block cipher is presented. By using both the structure of LBlock algorithm and the basic idea from the cube test, two neutral-bit detection algorithms are proposed. It is shown that all master key bits are involved in the each output of 9-round reduced LBlock cipher. Moreover, for given 18 cube variables, there still is nonexistence of key neutral-bit for 11-round reduced LBlock cipher. Research result shows that the full-round LBlock cipher has good key bits confusion against the classical cube attacks.

lightweight cipher; block cipher; key neutral-bit; cube test;box; LBlock cipher

1000-3428(2014)03-0028-05

A

TP309

国家自然科学基金资助项目(61100185)；广西自然科学基金青年基金资助项目(2011GXNSFB018071)；广西无线宽带通信与信号处理重点实验室(桂林电子科技大学)主任基金资助项目(11101)。

莫 钊(1987－)，男，硕士研究生，主研方向：分组密码分析；韦永壮，教授、博士。

2013-06-05

2013-08-02 E-mail：cw277346909@126.com

10.3969/j.issn.1000-3428.2014.03.006