注重过程教学 培养学生能力

刘文硕

摘 要：当前“重结果，轻过程”的“功利性”教学现象还普遍存在.本文从小学一位数学老师处理“数线段条数”的教法谈起，通过三个教学案例，从注重概念的形成过程；注重定理、公式、法则的发现过程；注重解题的思维过程等三个方面阐述了在课堂教学中如何注重教学内容的过程性设计，培养学生自主发展能力.

关键词：过程教学；能力；概念公式解题

当前“重结果，轻过程”的“功利性”教学现象还普遍存在.采用这种方式教学，表面上看教学效率很高，学生一下子就学会了解题方法，但数学教学不但要重视知识的传授，更应以学生发展为本，重在揭示获取数学知识与数学思想方法的思维过程，重在学生素质与能力的提高.案例：《中小学数学》（初中版）2009年第6期刊登方利生老师“这也是一种功利性教学”的文章，该文提到了小学四年级的一道习题：

请说出图1、图2、图3中分别有多少条线段，多少个角，多少个三角形？

文中指出：这种题目的设计意图是希望通过解答这样的问题，使学生学会解决计数问题的一种分类方法（不重不漏），即…….可小学老师的处理方法是：避开这种分类方法，简单地让学生记住：先数出最短的线段条数，5条，然后从这个条数开始加起，一直加到1为止，即5+4+3+2+1=15.这种教法看似简单、实用，但学生却失去了学习分类讨论思想方法的一次机会.……所以，看起来老师是在为学生降低难度，实际上是老师在逃避教学难点.这就是一种功利性的教学 [1 ]，对此我深有感触.这种“功利性”教学，其实是“重结果，轻过程”教学的典型体现.本文就课堂教学中如何注重教学内容的过程性设计，从三个方面谈些个人的体会.

一、课堂教学中应注重概念的形成过程

在传统教学中，教师对数学概念的教学常常采用“定义+例题”的模式进行，在概念的引入上着墨不够，没有给学生提供充分的概括本质特征的机会.这种忽略数学概念形成过程的教学模式，不符合学生的认知规律，不利于学生对概念本质的理解，导致学生创造力低，缺乏可持续发展的后劲.

笔者以为概念教学一般应遵循以下四个环节：首先应充分分析学生已有知识经验，设计具体实例让学生对概念形成初步感知；其次，要积极引导学生对各个具体实例中的共同特征进行分析、辨认，概括出本质属性，让学生形成丰富的数学概念表象；第三，应尝试让学生用自我语言对概念进行描述，然后在老师引导下对概念下定义；最后，让学生运用数学概念进行判断和解决数学问题.例如，在教“加权平均数”的概念时，老师先提出以下两个问题：

问题1 小敏同学在平时测试中的数学成绩分别为85分、90分、86分，他平时测试的平均成绩是多少？

问题2 小明同学在上学期平时测验的数学成绩是90分，期中考的数学成绩是92分，期末考的数学成绩是87分.按学校规定，平时成绩占20%，期中考试占30%，期末考试占50%，小明同学上学期的数学平均成绩是多少？

完成以上两个实例后让学生思考：平时测验、期中考试、期末考试的“重要程度”是不一样的，在本题中，哪些数据能够反映它们的重要程度？

通过以上两个具体实例，学生对“权”的含义有了感性的认识.接着老师抛出了问题3：某校初二年段共有三个班级，每个班级的人数及期末数学考试的人均成绩如表1：

表1

问：这个初二年段期末数学考试的人均成绩是多少？（精确到0.1）

在学生独立思考的基础上，教师将学生的不同解答展示在黑板上让学生讨论，通过引导与启发，使学生认识到86.1、81.3、90这三个数据在原问题中的“重要程度”是不一样的，而这三个数的重要程度可以由三个班级的人数40、45、43来反映，这三个数分别称为数据86.1、81.3、90的“权” [2 ].

至此，学生对“权”的概念有了丰富的表象，老师再让学生尝试用自我语言对“权”的概念进行描述，最后由师生共同概括归纳出加权平均数的概念.

二、课堂教学中应注重定理、公式、法则的发现过程

定理、法则、公式课的教学，不但要让学生掌握并会运用，更要通过定理、法则、公式的发现过程，培养学生思维能力和创新精神.但实际情况却是许多老师认为定理、法则、公式的探索推导过程费时费力，一般急于把结论直接呈现给学生，然后要求学生死记硬背结论，忽视其提出形成的过程，造成大量的学生知其然而不知其所以然，对公式、法则只能进行简单模仿，生搬硬套.因此，公式定理的教学课，应该注重数学知识的形成和发展过程，让学生充分经历探索、猜想、验证和归纳的一系列过程，并在此过程中渗透数学思想方法.例如在教平方差公式时，可按如下程序引导学生发现公式的生成发展过程：①给出一组多项式的运算如（x+y）（x-2）、（x+y）（x-y）、（x+1）（x-2）、（x-1）（x+2）、（x+1）（x-1）等；②引导学生观察运算结果的项数有什么不同？（有四项、有三项、有两项）让学生初步感知平方差公式的结构特征；③追问为什么会有项数不同？然后要求学生自己设计一道两个二项式的乘积，使运算的结果有两项；④让学生归纳出两个二项式的特点（两个二项式中有一项是相同的，另一项互为相反数）⑤引出平方差公式，给出文字说明和符号表达式；⑥引导学生用拼图验证公式的正确性；⑦给出一组式子如（2+x）（x-2）、（-x+2）（x-2）、（-x-2）（x-2）、（-x-2）（-x+2）等，让学生辨认哪些可运用平方差公式进行计算 [3 ].通过上述知识形成过程的教学，不但让学生掌握了平方差公式的本质（实际就是多项式乘以多项式，只不过结果只有两项）和结构特征，又培养了学生的观察能力、分析能力、归纳概括能力，同时又渗透了“数形结合”的数学思想方法.

三、课堂教学中应注重解题的思维过程

数学课堂中离不开解题教学.黄金声老师归纳总结出“讲题的四种境界”，即第一种境界：就题讲题，把题目讲清（达成目标：一听就能懂）；第二种境界：发散题目的多种解（证）法，拓展解题思路，把题目讲透（达成目标：一点就能透）；第三种境界：理清题目的诸多变化，以求探源奠基，把题目讲活（达成目标：一时忘不了）；第四种境界：探究题目之数学思想方法，以能力培养为终极目标，做题目的主人（达成目标：一用真有效） [4 ].由此可见，解题教学并不是让学生一听就懂就完成了教学任务，如文前所提到的这位小学教师的讲题方法，虽然学生一听就会，并会解决一类简单问题，但该题蕴含的重要数学思想方法就丢掉了，失去了应有的教育价值.因此，解题教学也应着眼于过程性的体现，让学生经历数学知识的形成与应用过程.

例如，待定系数法是一个很重要的数学方法.在应用它解决数学问题的过程中，其实涉及了参数、方程、从特殊到一般等数学思想方法.在实际教学中，大部分老师处理的方法是先给出一个例题（如：已知y是x的正比例函数，且当x=3时，y=24，求y与x之间的函数解析式），再总结解题的四个步骤：“一设（设函数式y=kx）、二代（将x=3时，y=24代入）、三解（解出k）、四回（把解出的k值回代到函数式里）”，让学生依样画葫芦操练，而不去理解它的本质，感悟它的形成过程.这样的教学方式，学生只会死记硬背，容易遗忘，没办法形成知识体系.在我校的一次公开课上，开课老师设计了如下的教学环节，更容易让学生感悟“怎么想”的过程.

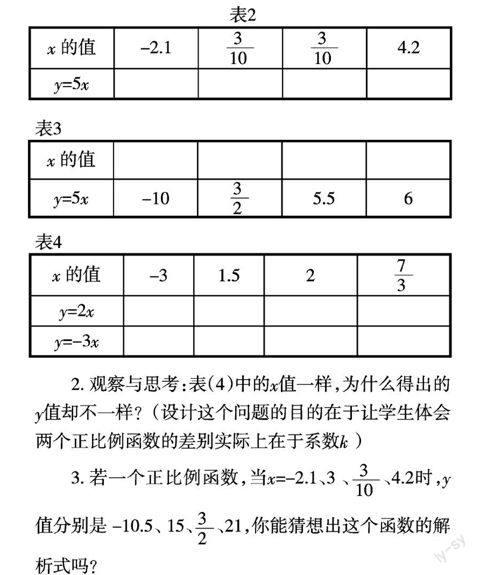
1. 填写表2—表4：

表2

表3

表4

2. 观察与思考：表（4）中的x值一样，为什么得出的y值却不一样？（设计这个问题的目的在于让学生体会两个正比例函数的差别实际上在于系数k ）

3. 若一个正比例函数，当x=-2.1、3 、■、4.2时，y值分别是 -10.5、 15、■、21，你能猜想出这个函数的解析式吗？

4. 老师直接指出，我们遇到了相反的问题.在填表中是“已知正比例函数解析式和给出的x值，求相应的y值”，现在是知道了“一系列x值和与其相对应的y值，求函数解析式”，其实质是求k的值.

5. 进一步发问：只求一个值k，要不要那么多数据呢？

6. 回到例题：已知当x=3时，y=24，求正比例函数的解析式.

讲解该例题时先引导学生用“笨”办法去“凑”：假如这个函数是y=2x， y=3x行吗？让学生体会到，求正比例函数解析式难在求k，进一步引导学生想一想，当时为什么要学方程？这样就自然想到了要设未知数k参与运算.这种教法设计，看似把简单问题复杂化了，但却充分暴露了解题的思维过程，有利于学生数学知识的形成与发展和数学思想方法的渗透.此外，解题过程教学还应注重解题后的反思，探索一题多解和一题多变，培养学生良好的思维习惯.

总之，“重结果，轻过程”的功利性教学不利于学生思维品质和创新能力的培养，与现行的新课标理念背道而驰.因此，教师在课堂教学中应真正以学生为本，注重教学内容的过程性设计，让学生经历学数学中“做数学”的过程，培养学生自主发展能力，为今后终身发展奠定基础.

参考文献：

[1]方利生.这也是一种功利性教学[J].中小学数学（初中），2009（6）.

[2]朱学燕.我教加权平均数[J].中小学数学（初中），2009（7-8）.

[3]陈东革.初中数学公式教学初探[J].中小学数学（初中），2010（1-2）.

[4]黄金声.讲题的四种境界[J].数学通报，2009（10）.