大型储罐角焊缝焊趾表面裂纹应力强度因子数值计算

魏化中 张占武 丁克勤 舒安庆,2

(1.武汉工程大学机电工程学院；2.武汉市压力容器压力管道安全技术研究中心；3.中国特种设备检测研究院)

随着国家石油战略储备库和一批大型商业油库的建成，目前国内在役的10万m3及以上的储油罐已有数百台，这些储罐的安全运行意义重大。储罐常见的失效模式包括腐蚀和开裂，对于裂纹失效模式，最常见的是角焊缝焊趾裂纹。大型储罐盛装的介质大多腐蚀性较强，而且角焊缝处于结构不连续区域，因此角焊缝裂纹的开裂机理一般属于较低应力水平的应力腐蚀开裂，可作为线弹性断裂问题来处理。对裂纹的研究，应力强度因子是控制线弹性断裂的重要参量，如果使用双参数失效评定图来进行裂纹缺陷安全评价，应力强度因子也是需要计算的重要基础数据。求解应力强度因子的方法主要有解析法、实验法和数值法，笔者采用数值法中的有限元法对储罐角焊缝焊趾表面裂纹进行建模求解。

采用有限元法求解储罐角焊缝焊趾表面裂纹应力强度因子有两个难点，一是裂纹及其扩展层有限元模型建立的复杂性。有限元法建立裂纹模型常用的方法是1/4节点奇异单元法，其难点在于裂尖奇异单元中节点的添加和奇异单元的扩展[1]。1/4节点的添加可以通过ANSYS中的宏命令FRACT来实现；奇异单元扩展成整体模型则是建模的关键，笔者提出利用混合网格扩展方法实现裂纹奇异单元到整体有限元模型的扩展。二是大型储罐焊趾位置应力状态复杂。大型储罐的地基一般采用混凝土环梁地基与砂土地基组合的方式，在受压的情况下两地基的交界位置会发生不均匀沉降，导致一段边缘板翘离底面。这给理论公式计算罐壁下节点的应力带来很大工作量，需要假设一段翘离长度进行反复试算[2]。常用有限元软件模型为罐底板-地基接触模型。由于计算焊趾表面裂纹需要进行三维建模，三维的接触分析属于非线性分析，加之大型储罐有限元模型网格较多，计算一次耗时很长，且裂纹应力强度因子计算又要进行大量重复计算，必须建立可用于大量重复计算的有限元模型进行求解。针对焊趾部位应力场求解的困难，笔者讨论了3D简化约束模型用于变参数裂纹应力强度因子的求解。

1 混合网格扩展方法

文献[3～5] 讨论了关于裂尖奇异单元模型的建立。ANSYS VM143中给出了构造裂尖奇异单元最关键的一步——添加1/4节点的宏命令FRACT。在此基础上讨论裂尖奇异单元扩展成整个计算模型的方法。对于不复杂结构，可以通过逐节点扩展法扩展成六面体的整体模型(图1)。在ANSYS中先确定边界点，利用FILL命令填充节点，再通过生成单元的命令由节点生成单元，对于平板或者简单圆筒体可以利用逐节点扩展方法。对于复杂结构，逐节点扩展法的工作量则比较大，这种方法并不实用，但可以采用混合网格扩展方法进行扩展，其建模过程如图2所示。文献[6]利用混合网格扩展法进行裂纹及其扩展模型建模，并利用多节点耦合(MPC)方法处理连接的交界面。

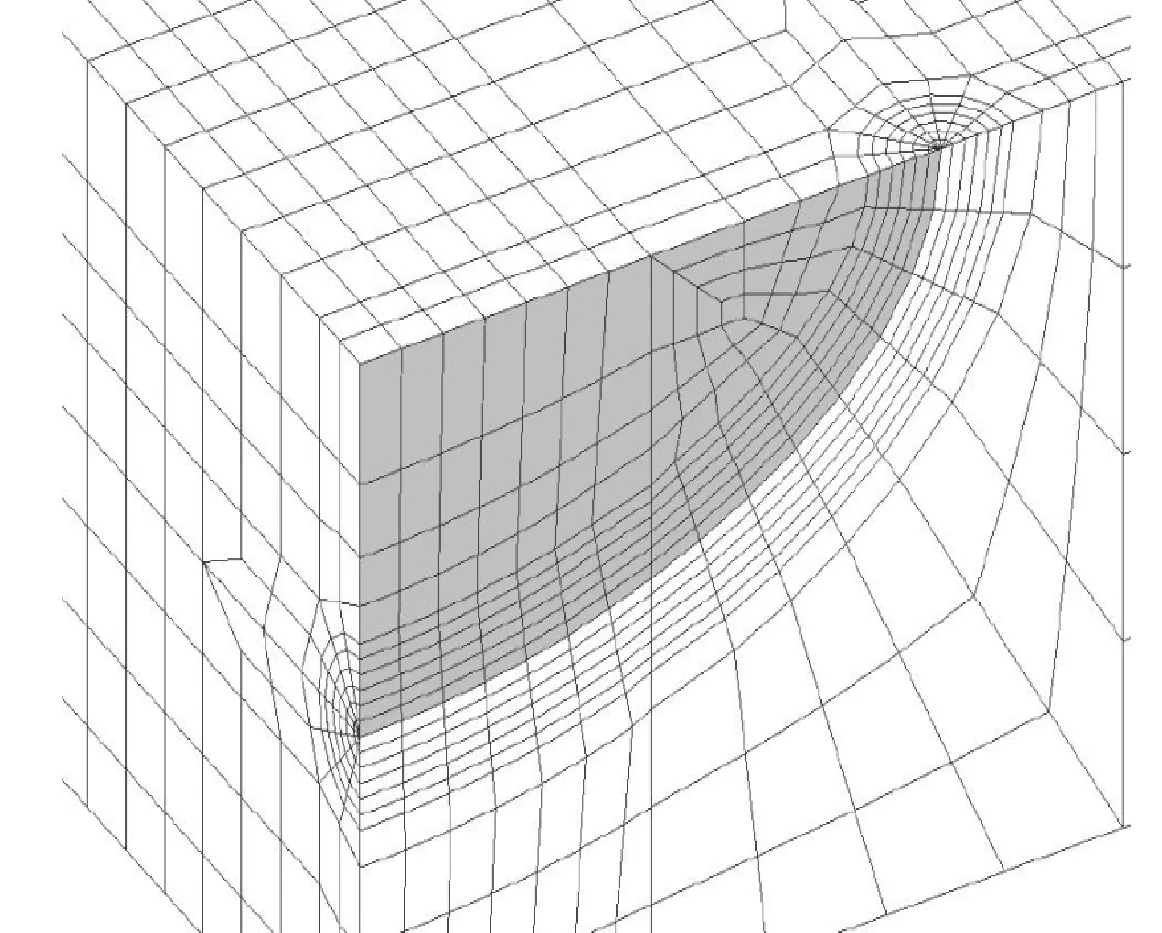
图1 逐节点生成的1/4平板半椭圆裂纹模型

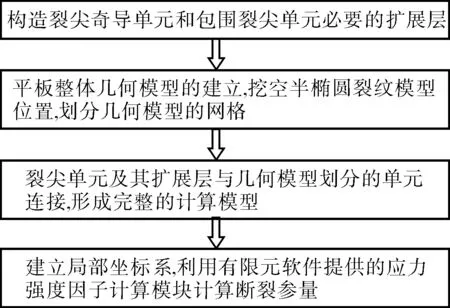
图2 混合网格扩展法建模过程

以平板表面半椭圆裂纹为例来说明混合网格扩展法的实现过程，储罐角焊缝焊趾表面裂纹有限元模型可通过类似方法建立。通过逐节点建模法建立奇异单元及其包围层，沿椭圆裂纹前沿建10段单元，每段单元跨过的角度按照椭圆弧长的等分数换算得到。每段中裂尖单元沿圆周方向划分16段，每段角度为22.5°。奇异单元的尺寸和裂纹深度比对应力强度数值影响显著。对于此次平板裂纹建模计算，裂尖奇异单元尺寸和裂纹深度比Lq/a保证在0.01 ～0.04之间[7]，奇异单元包围层和奇异单元尺寸间隔比设置为1。

利用混合网格扩展法将裂尖奇异单元及其包围层与整体模型连接。奇异单元及其包围层建好之后建立外围几何模型，并把裂尖单元及其扩展层的位置挖空；外围的几何模型划分完网格之后，将奇异单元及其扩展层的网格和几何模型上的网格进行连接，保证交界面具有公共节点。图3～5显示了奇异单元及其包围层与整个模型连接的过程。

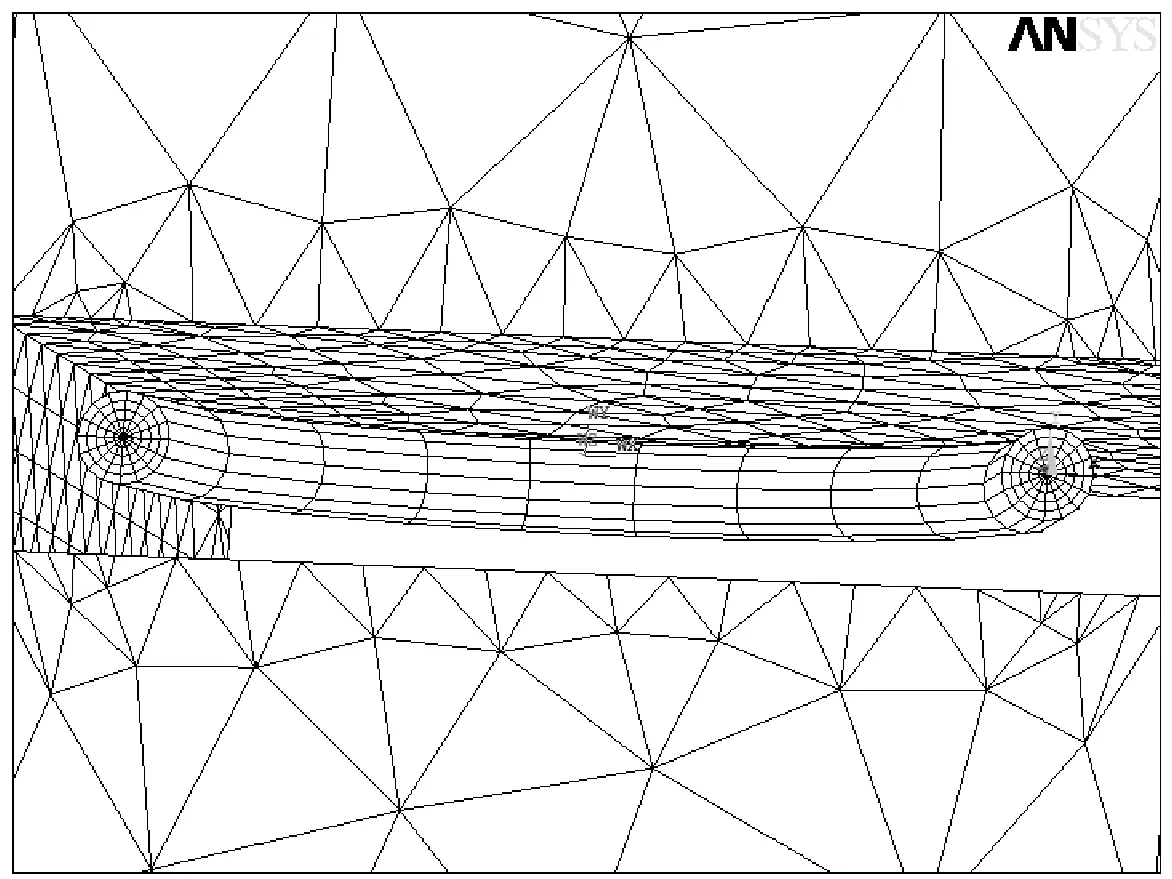
图3 奇异单元及其扩展层的几何模型

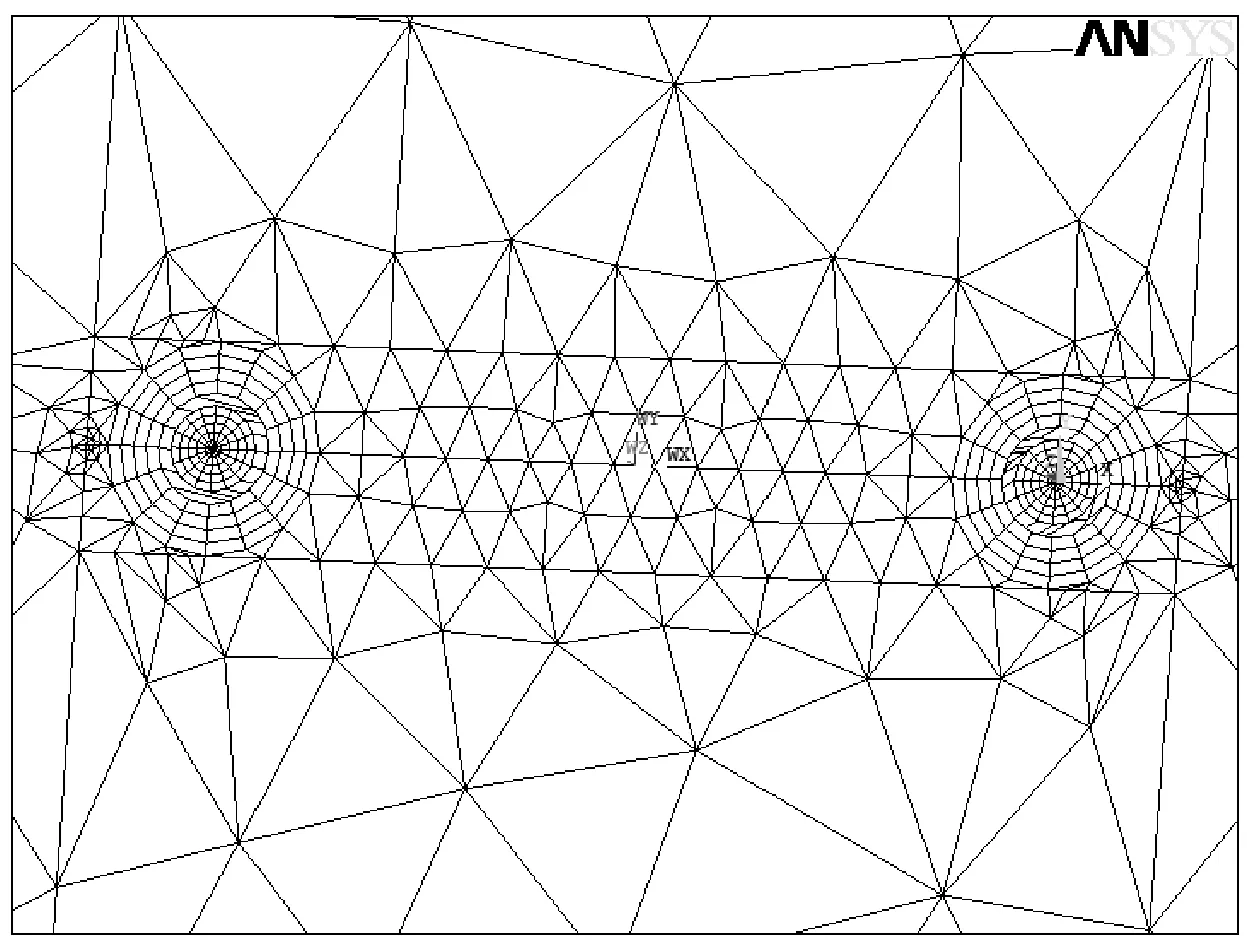
图4 网格连接之后的几何模型

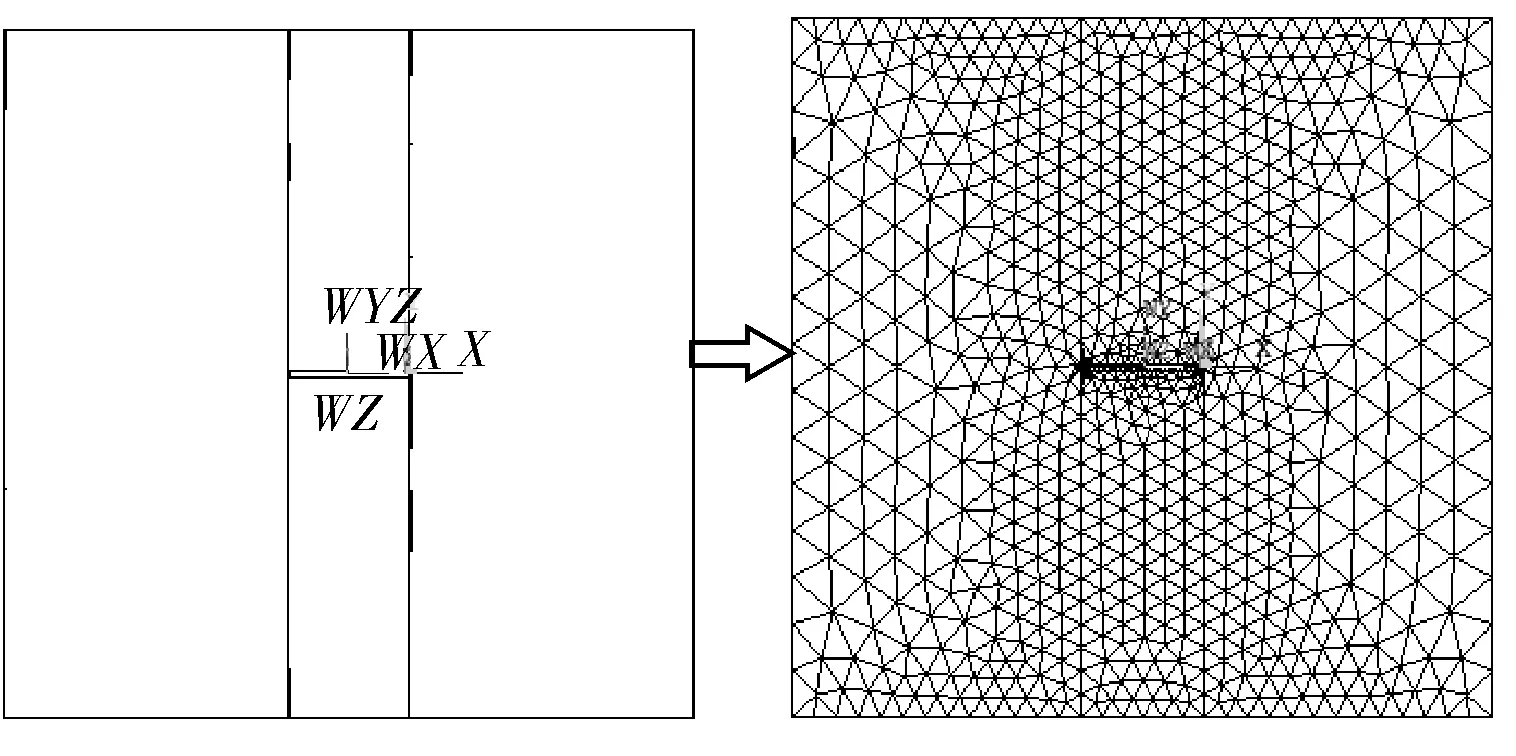
图5 平板表面半椭圆裂纹

2 储罐角焊缝焊趾表面裂纹应力强度因子有限元计算

2.1 3D简化约束模型

笔者的研究计算对象为一个15万m3储油罐，该储油罐的结构参数如图6所示。本算例的大型储罐有10层壁板，第一至七层的材料为SPV490Q高强度钢，第八层的材料为16MnR，第九、十层和包边角钢的材料为Q235A。底板的边缘板材料为SPV490Q，中幅板材料为Q235A。材料属性见表1。

图6 15万方储罐的结构参数

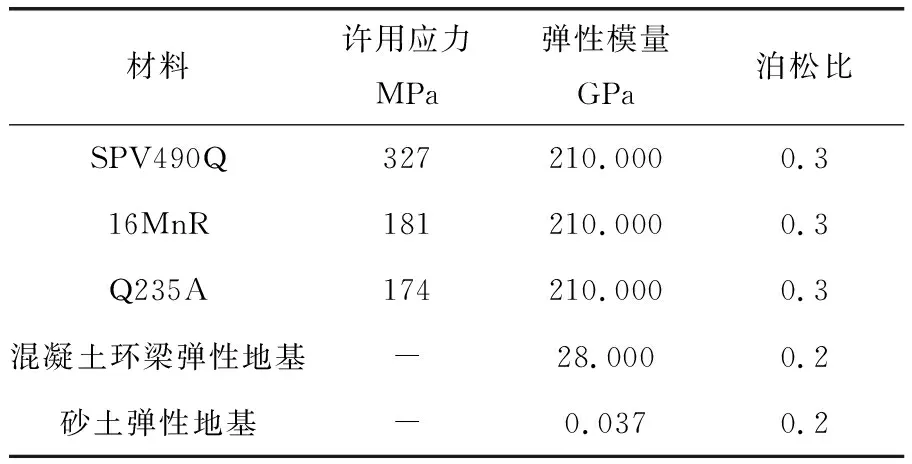
材料许用应力MPa弹性模量GPa泊松比SPV490Q327210.0000.316MnR181210.0000.3Q235A174210.0000.3混凝土环梁弹性地基-28.0000.2砂土弹性地基-0.0370.2

计算储罐角焊缝焊趾表面裂纹的应力强度因子必须先得到焊趾部位的应力分布。计算载荷条件是罐体自重和介质的液压，充装系数为0.8。储罐有限元建模方法常用的有罐底板-地基接触模型和3D双线性LINK10弹性约束模型。由于三维裂纹变参数重复计算的要求，笔者采用3D简化约束模型(图7)，该模型在底板翘离部分不加支撑[8]，翘离部分长度由2D罐底板-地基接触模型计算得到。在边缘板和地基接触端加轴向约束，对和地基接触的中幅板和未翘离地基的边缘板则和地基建成一体的模型，在边界划分出公共节点。对称轴上和地基底端的约束和接触模型一致，在对称轴上加径向约束，地基底端加轴向约束。笔者建立的是储罐的1/360模型，还需要在纵截面上施加对称约束。该模型经对比计算结果和罐底板-地基接触模型非常接近，可以替代3D接触模型用于变参数裂纹的重复计算。

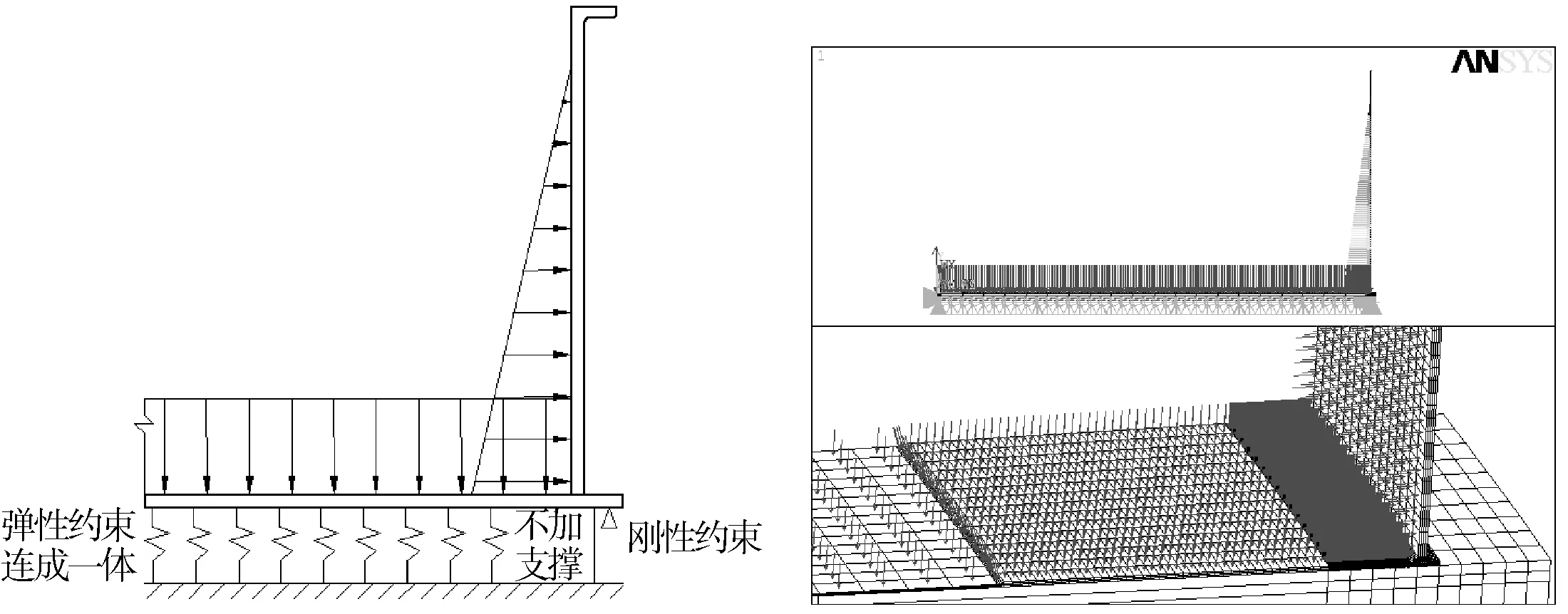
图7 3D简化约束模型边界条件示意图

2.2 储罐角焊缝焊趾表面裂纹模型的建立

储罐焊趾表面半椭圆裂纹的有限元建模方法和平板表面半椭圆裂纹类似，但整体模型结构更加复杂。裂尖奇异单元及其包围层仍然通过逐节点建模方法建立，通过混合网格扩展方法得到整体有限元模型。整体模型部分通过常规建模方法先建立几何模型，在几何模型上把裂纹部分挖去，划分网格得到有限元模型，再将裂纹奇异单元及其包围层和整体模型网格进行连接得到完整的有限元模型。储罐角焊缝焊趾表面裂纹示意如图8所示。

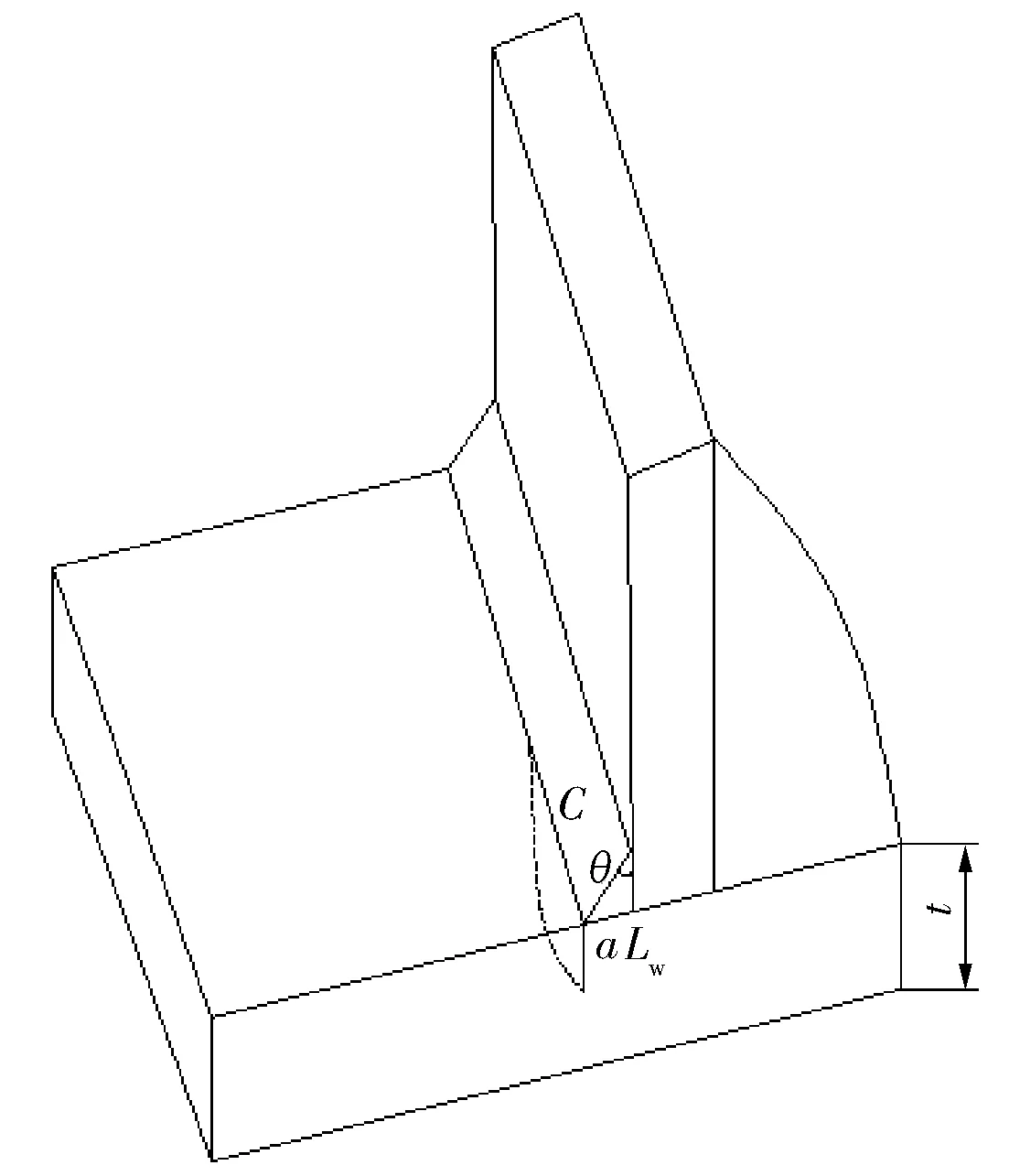
图8 储罐焊趾表面裂纹示意图

根据T形连接焊趾表面裂纹的表达式[9]，焊趾表面裂纹应力强度因子的表达式可以写为：

(1)

式中F——形状系数，无量纲；

KT——应力强度因子，N/mm3/2；

Mk——焊接放大系数，无量纲；

σb——弯曲应力分量，MPa；

σm——薄膜应力分量，MPa；

φ——第二类椭圆积分，无量纲。

式(1)中的焊接放大系数Mk由裂纹深度半长比a/c、裂纹深度板厚比a/t、焊脚尺寸板厚比Lw/t和焊趾角θ决定，用函数的形式记为：

(2)

从式(1)、(2)可以看出，应力强度因子KT主要由a/c、a/t、Lw/t和焊趾角θ决定。笔者讨论了上述参数变化对应力强度因子数值的影响。在变参数求解过程当中设定储罐的板厚t总是不变。讨论应力强度因子随裂纹深度半长比a/c变化规律时，焊脚尺寸板厚比Lw/t值不变，焊趾角θ不变，裂纹半长度c不变，只改变裂纹深度a；讨论应力强度因子随裂纹深度板厚比a/t变化规律时，焊脚尺寸板厚比Lw/t不变，焊趾角θ不变，裂纹深度a和裂纹半长c均变化，但是a/c=0.50保持不变；讨论应力强度因子随焊脚尺寸板厚比Lw/t变化规律时，裂纹深度半长比a/c=0.500保持不变，裂纹深度板厚比a/t=0.45保持不变；讨论应力强度因子随焊趾角θ变化规律时，裂纹深度半长比a/c=0.50保持不变，裂纹深度板厚比a/t=0.45保持不变。

3 计算结果讨论

3.1 应力计算结果

储罐角焊缝焊趾表面裂纹的开裂主要与裂纹面的径向应力有关，储罐角焊缝焊趾裂纹开裂如9所示。设置两条路径考察径向应力的变化(图10)：第一条沿径向设置路径，考察径向力沿径向的变化；第二条沿焊趾厚度方向设定路径，考察径向应力沿厚度方向的变化。

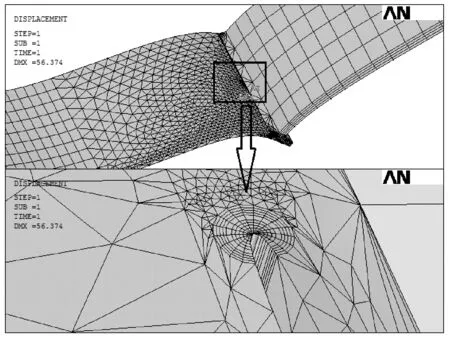
图9 储罐角焊缝焊趾裂纹开裂

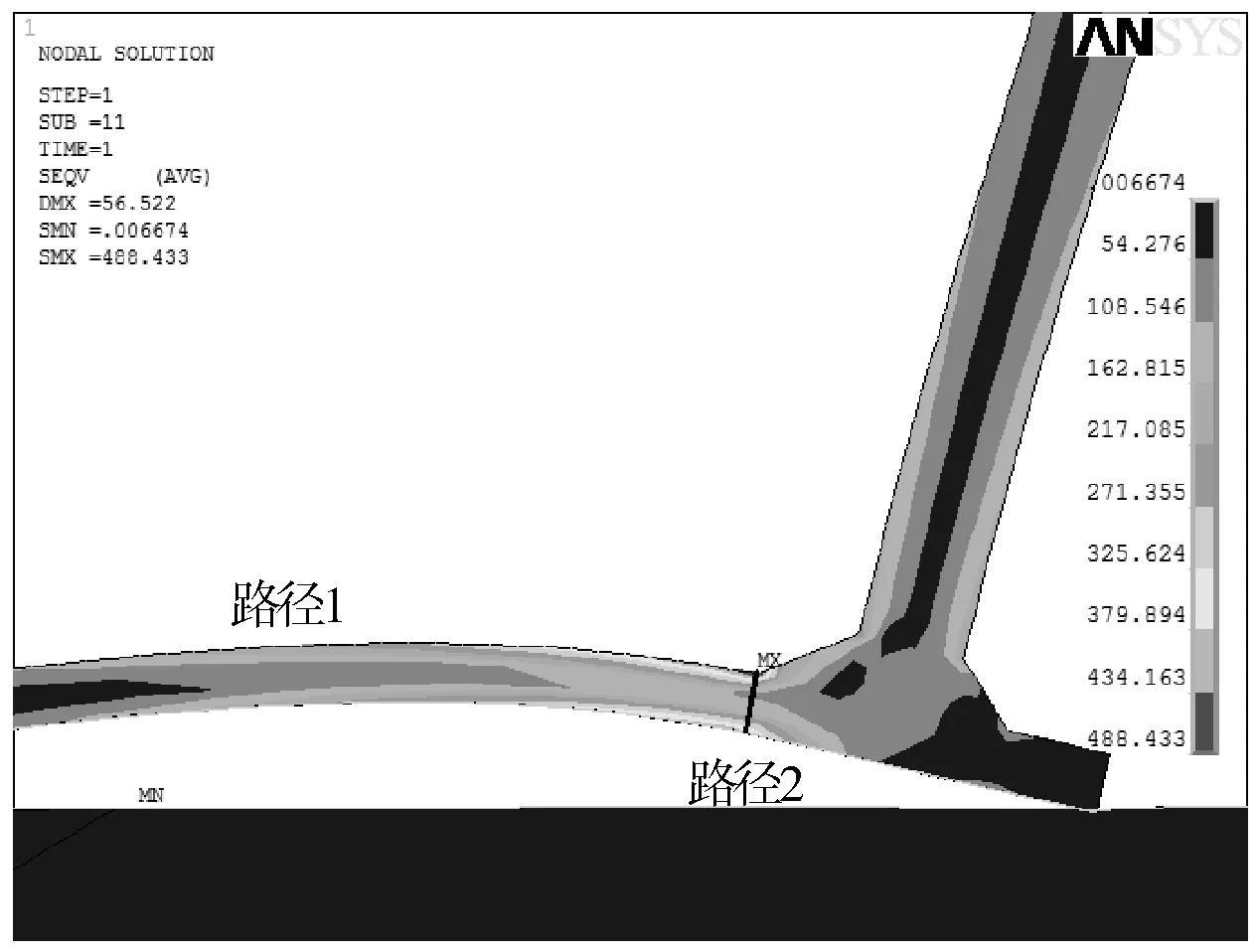
图10 路径设置

罐底板径向应力沿径向的变化分布曲线如图11所示，从图11可以看出，在角焊缝焊趾位置径向应力水平最高，这是导致裂纹开裂最主要的应力。随着径向长度的增加，径向应力迅速衰减，大部分边缘板和中幅板的应力水平都很小。

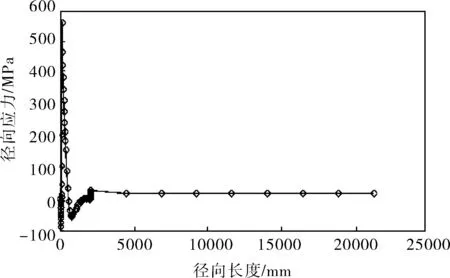
a. 底板内表面径向应力

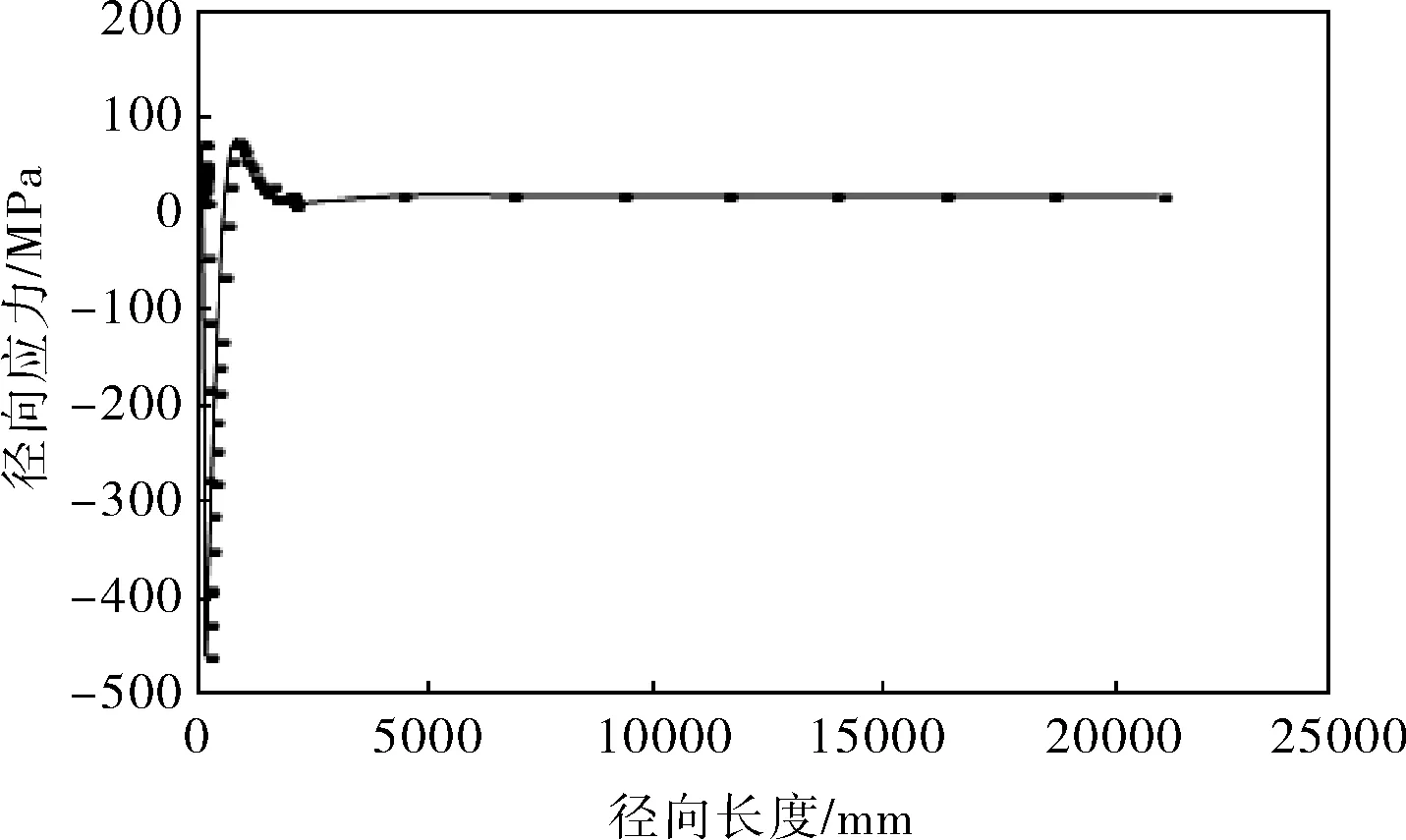
b. 底板外表面径向应力

径向应力沿焊趾厚度方向变化曲线如图12所示，从图12可以看出，在内表面上为拉应力，在外表面上为压应力，随着厚度的增加应力值逐渐减小。

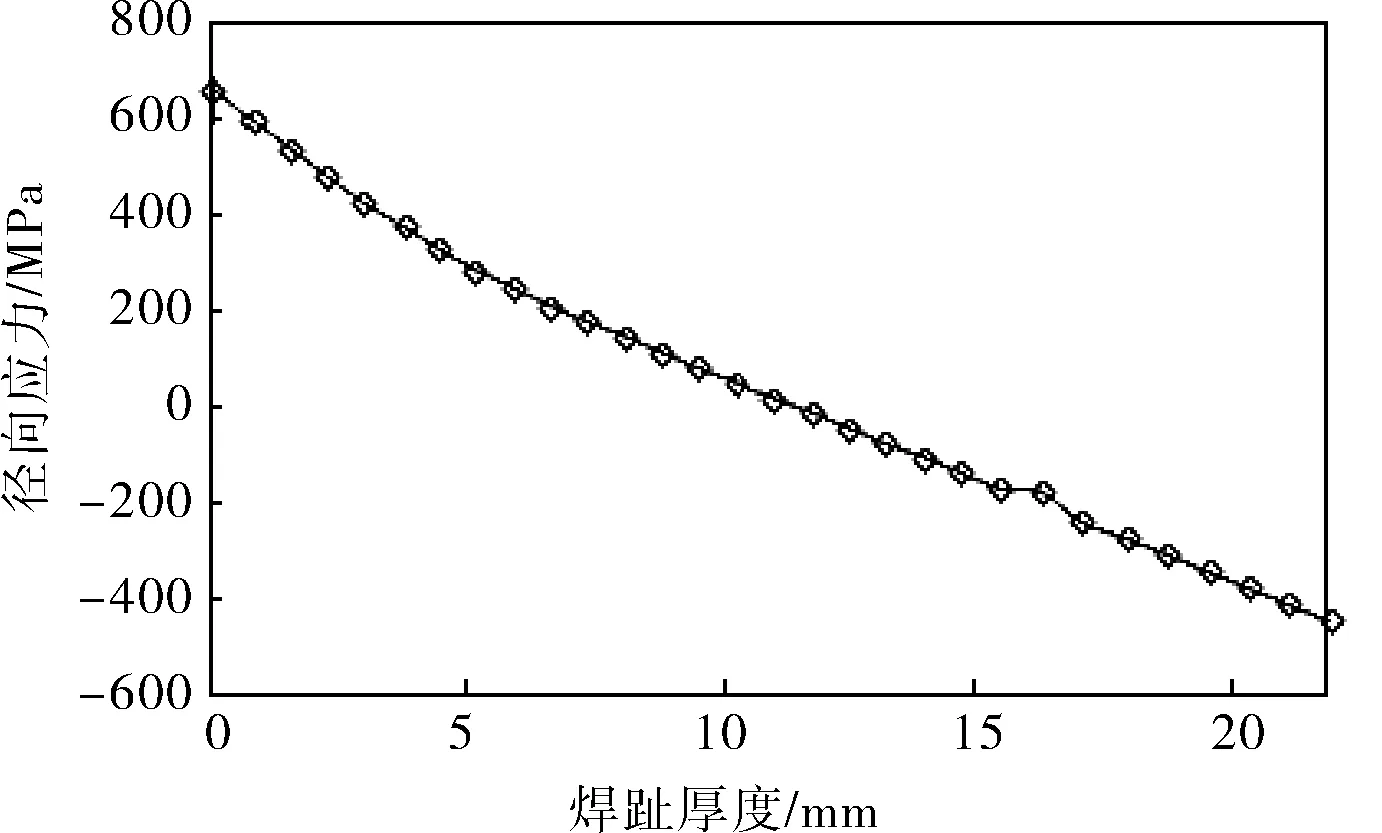
图12 径向应力沿焊趾厚度方向变化

3.2 应力强度因子计算结果

从储罐角焊缝焊趾表面裂纹应力强度因子随a/c的变化曲线(图13a)可以看出，对于某一确定的a/c值，应力强度因子数值分布呈U形分布，在表面点应力强度因子数值取的最大，随着裂纹前沿节点角度φ的增大，应力强度因子数值逐渐减小，0～90°和90～180°呈对称分布；对于变化的a/c值，由于c是不变的，a/c值的增大也就是裂纹深度a值的增大，随着裂纹深度a值的增大，在表面点上应力强度因子增大，而在最深点应力强度因子有减小的趋势。因为随着裂纹深度的增加，径向拉应力降低，深度继续增加之后变为径向压应力，这与上面计算得到的焊趾位置径向应力随厚度方向的变化是一致的。

储罐角焊缝焊趾表面裂纹应力强度因子随a/t的变化曲线(图13b)与随a/c的变化曲线类似：对于某一个确定的a/t值，表面点的应力强度因子数值最大，随着裂纹前沿节点角度φ的增加，应力强度因子数值下降，0～90°和90 ～180°的数据呈对称分布；对于变化的a/t值，因为设定板厚t是不变的，a/t值的增大也就是裂纹深度a值的增大，随着裂纹深度的增加，应力强度因子的值呈下降趋势。

从储罐角焊缝焊趾裂纹应力强度因子随Lw/t的变化曲线(图13c)可以看出：对于某一确定的Lw/t,应力强度因子在表面点取的最大，随着裂纹前沿节点角度φ的增加，应力强度因子数值下降；对于变化的Lw/t,其值增大时在表面点上的应力强度因子数值变大，但在最深点的应力强度因子数值减小。

从储罐角焊缝焊趾裂纹随焊趾角θ变化曲线(图13d)可以看出：对于某一确定的焊趾角θ，应力强度因子在表面点取的最大，随着裂纹前沿角度φ的增加，应力强度因子数值逐渐减小，0～90°和90～180°数值呈对称趋势；对于变化的焊趾角θ，随着θ的增大，不管是在表面点和最深点应力强度因子数值都呈下降趋势。

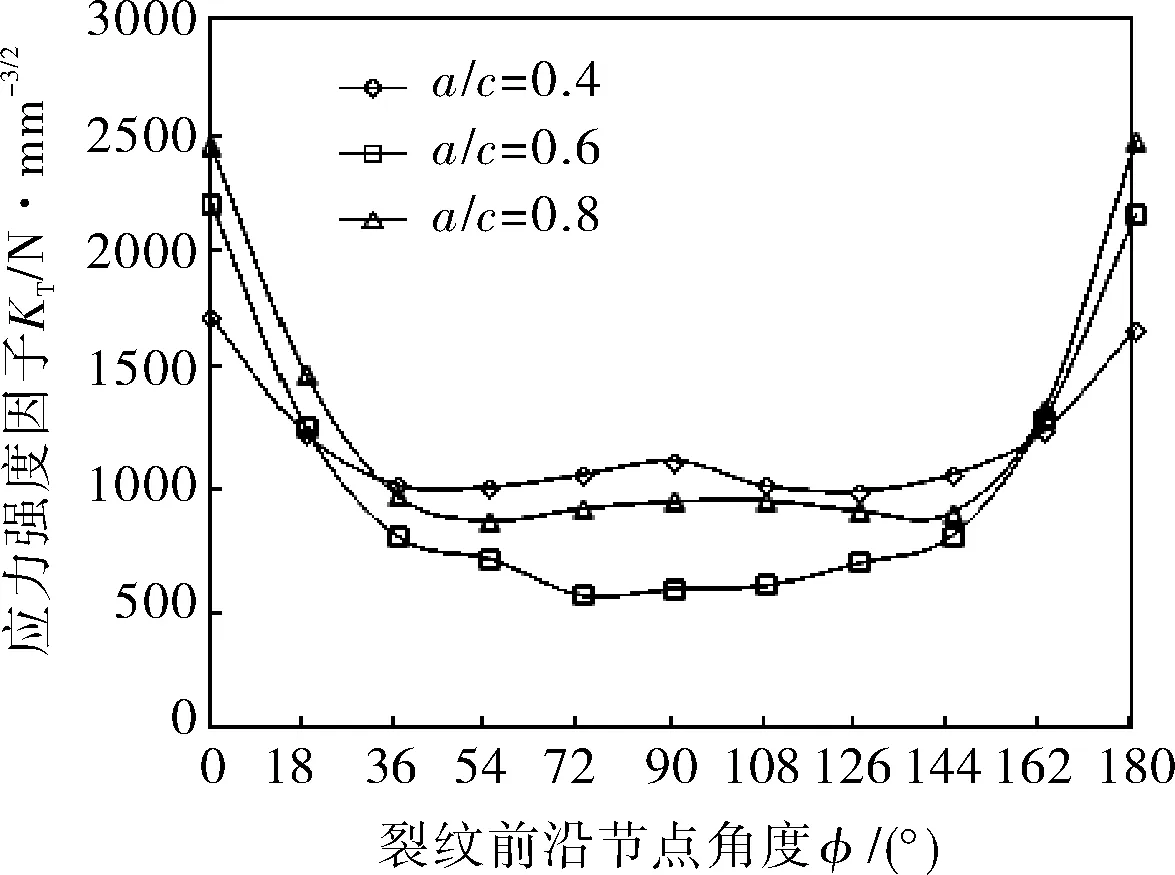
a. 裂纹深度半长比a/c

b. 裂纹深度板厚比a/t

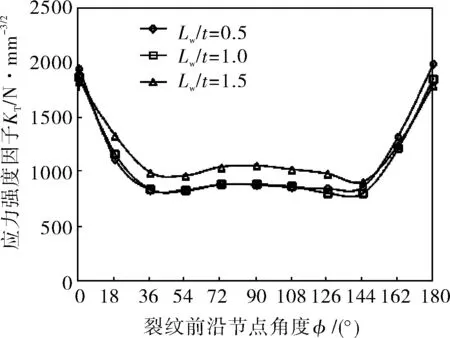
c. 焊脚尺寸板厚比Lw/t

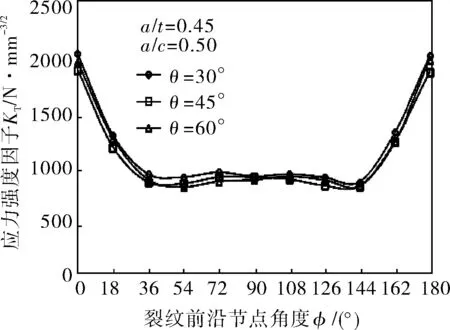
d. 焊趾角θ

4 结束语

针对大型储罐的典型失效模式——角焊缝开裂，研究了角焊缝焊趾表面裂纹的有限元建模计算方法。采用1/4节点奇异单元法建立裂尖单元，提出一种混合网格扩展方法对裂纹奇异单元进行扩展。采用3D简化约束模型来计算变参数裂纹的应力强度因子。计算结果表明：对于某一确定参数的裂纹，应力强度因子数值沿裂纹前沿呈U形分布。和均匀拉伸平板表面裂纹应力强度因子在最深点取值最大不同，储罐角焊缝焊趾表面裂纹应力强度因子在表面点取的最大。对于变参数裂纹，随着裂纹深度的增加，表面点的应力强度因子有增大趋势，最深点的应力强度因子数值有下降趋势，这与沿焊趾厚度方向裂纹面上的径向应力分布趋势是一致的，同时又反应了裂纹应力强度因子的几何尺寸效应。计算结果可作为进一步对裂纹进行安全评价的基础数据。

[1] Barsoum R S.Application of Quadratic Isoparametric Finite Elements in Linear Fracture Mechanics[J]. International Journal of Fracture,1974,10(4):603～605.

[2] 徐英，杨一凡，朱萍.球罐和大型储罐[M].北京：化学工业出版社，2005.

[3] 徐华.结构断裂分析的奇异等参元和广义参数有限元法[D].南宁：广西大学,2006.

[4] 陈银强.圆柱体表面椭圆裂纹应力强度因子的有限元分析和研究[D].武汉：武汉工程大学，2006.

[5] 董硕.含肩部穿透裂纹接管安全评定[D].大连：大连理工大学，2010.

[6] Bremberg Daniel,Dhondt Guido. Automatic 3-D Crack Propagation Calculations:a Pure Hexahedral Element Approach Versus a Combined Element Approach[J]. International Journal of Fracture,2009,157(1/2):109～118.

[7] 王永伟，林哲.表面裂纹的三维模拟及应力强度因子计算[J].中国海洋平台，2006，21(3):23～26.

[8] 沈建民.大型油罐的静强度及动力响应分析[D].杭州：浙江大学，2006.

[9] Fu B, Haswell J V,Bettess P.Weld Magnification Factors for Semi-elliptical Surface Cracks in Fillet Welded T-butt Joint Model[J].International Journal of Fracture,1993,63(2):155～171.