迷思概念、相异构想与儿童数学教学

汪树林

（如皋市港城实验学校 江苏 如皋 226532）

儿童在正式的数学学习之前，通过对日常生活的现象观察和体验，形成了一些前数学概念、经验和儿童阶段特有的思维方式。当儿童正式学习数学时，这些非正式的数学概念、经验或思维方式会同正式的数学概念、新知混淆、“打架”，甚至某些错误的前数学概念、经验会占上风，学者将这类错误概念称为“迷思概念”，将这类错误的认知、思维结构或方式称为“相异构想”或“不同的解释框架”。儿童数学的迷思概念、相异构想干扰着儿童的新知理解，甚至让儿童错误地“同化”新知。作为教师，必须高度重视这一现象，尽量降低迷思概念、相异构想对学生数学学习带来的消极作用。

一、聚焦：儿童数学迷思概念、相异构想的特质解读

儿童头脑中的迷思概念、相异构想是儿童在数学学习过程中的正常现象，它与其他学习问题诸如听课注意力不集中、做题粗心大意、作业磨蹭等现象相比，有着自身独特的性质。

1.自发性。儿童的迷思概念、相异构想是儿童在其观察与体验周围世界的过程中通过直觉与无科学根据的想象自发形成的，是零散的、无组织、无系统的。如儿童会认为“扇形就是像扇子一样形状的图形”“角的两条边画得越长角越大”“周长长的长方形面积就大”等。

2.肤浅性。由于儿童自发性的认识，他们在大脑中形成的概念、判断与推理往往缺乏逻辑性，他们认识概念、思考问题往往比较肤浅，只停留在表象阶段，不能正确地通过具体表象形成抽象概念，自然也就无法把握数学的本质。如儿童会认为“一千克铁比一千克棉花重”“甲数比乙数多，乙数就比甲数少”“平行四边形都是轴对称图形”等。

3.隐蔽性。由于教师对儿童迷思概念、相异构想并不去深究其成因，这就让迷思概念、相异构想暗藏于儿童的学习过程之中。如儿童可能会准确地背诵出“每相邻两个长度单位、面积单位、体积单位之间的进率”，但一到做具体习题时，总是把相邻体积单位之间的进率误解为面积单位之间的进率，或把相邻面积单位之间的进率误解为长度单位的计算进率等。

4.顽固性。由于迷思概念、相异构想并不是儿童主观意识的产物，所以，即使经教师或同伴提醒当时能纠正过来，但在遇到同类信息对象时，儿童可能还会因淡忘其数学本质从而导致“错过的”还是“一错再错”。如儿童在学习小数前可能具有“小数很小”的迷思概念，通过学习可能表面上澄清了这一错误认识，但到一定时候，儿童潜意识中还会把小数与正纯小数混淆从而导致解题错误。

二、剖析：儿童数学迷思概念、相异构想的成因透视

迷思概念、相异构想广泛地存在于小学各年级段的儿童头脑中，也广泛地存在于小学数学各个知识模块中（计算、概念、问题解决等）。其主要来源即成因可以归结为以下几方面：

1.儿童的直觉经验

儿童由于缺乏必要的数学方法和“数学式思维”,往往凭借自己的直觉形成了朴素、片面的认识。如儿童看到题目中“一共”二字就用“加法”，看到“还剩”二字就用减法；画几条直线，儿童往往认为斜画的不是直线，只有水平方向和铅垂方向的才是直线；学习“圆锥的认识”，儿童凭直觉往往会认为圆锥的侧面展开图是三角形。教学中教师必须引导儿童开展“数学实验”进行验证，如可以让儿童用直尺验证斜线的曲直，用软纸做圆锥，然后再让儿童沿着圆锥的母线剪开。通过数学实验，儿童会惊奇地发现，原来圆锥的侧面展开图是扇形。如此，不仅改变了儿童由直觉而带来的迷思概念、相异构想，而且让儿童领悟到学习的重要方法——“做中学”。

2.类化概念的干扰

数学学科中存在着许多字面相近、属性相关、含义相似而不同的概念，即类化概念。由于它们之间对比度小，个性欠鲜明而导致儿童感知结果接近。在思维过程中，儿童会产生误导性联想和思维分歧化，出现概念间本质属性的混淆。如“扩大”与“增加”、“缩小”与“减少”、“速度的平均数”与“平均速度”、“倍”与“倍数”、“半圆的周长”与“圆周长的一半”等。

3.日常生活的影响

儿童在日常生活中对周围获得了一些感性表象，积累了感性经验，其中有一些是正确的，有助于理解和掌握数学新知，而更多的则是片面的、错误的。如“生活角”（“墙角”“桌角”等）对学习“数学角”的干扰，生活中“质量”概念对数学中“质量”概念的干扰，生活中在水平线参照基础上的“竖直线”对数学中“垂直线”的干扰等。

4.儿童的记忆、思维定势或心理暗示

儿童因先前累积的学习经验而初步形成了记忆定势，当遇到类似的学习情境时，容易“想当然”地将新问题按以往解决旧问题的方式解决，并潜意识地想象着结果朝着自己所期待的方向发生。如儿童受“一个数除以同一个数等于1”的心理暗示，容易误认为“4×5÷4×5=1”；受“甲比乙多多少，乙就比甲少多少”的思维定势或心理暗示，容易误认为“甲比乙多25%，乙就比甲少25%”等。

除上述主要成因外，儿童的知识基础、儿童因逆反心理而对正确概念的排斥、生活中的传统观念、儿童的消极思维惰性、某些资料对数学概念的不科学阐释等，也无时无刻不在影响着儿童对数学新知的理解和掌握。

三、突破：儿童数学迷思概念、相异构想的转变策略

针对儿童数学学习过程中客观存在的迷思概念、相异构想，教师要理性地分析其产生根源，运用多种途径、方法去探寻处于隐蔽地带的迷思概念、相异构想，帮助儿童判断、识别、纠正自己的已有经验与概念，尽量降低迷思概念、相异构想对儿童数学学习的副作用，从而提升儿童的学习品质。

1.探寻儿童“前数学经验”，是纠正迷思概念、相异构想的前提

探寻儿童“前数学经验”最有效的方法是对儿童的已有知识经验进行诊断性评价。教师要把握儿童原有知识与认知结构，尤其是那些错误的概念、思维方式或学习习惯。可以对儿童进行数学问卷调查，与儿童进行数学座谈、数学讨论等，让儿童暴露迷思概念、相异构想，据此确定教学起点、教学方法，进而准确地预设教学。

教学国标苏教版小学数学四年级下册《三角形》单元时，笔者将教学目标锁定为：（1）概括三角形的定义。（2）认识三角形各部分的名称及底和高的含义，学习用字母表示三角形，学会画高。（3）了解三角形的稳定性。分析学情后发现，孩子们有很多知识已掌握或部分掌握，但也存在着认识误区，这里笔者用表格说明（参见表1）。

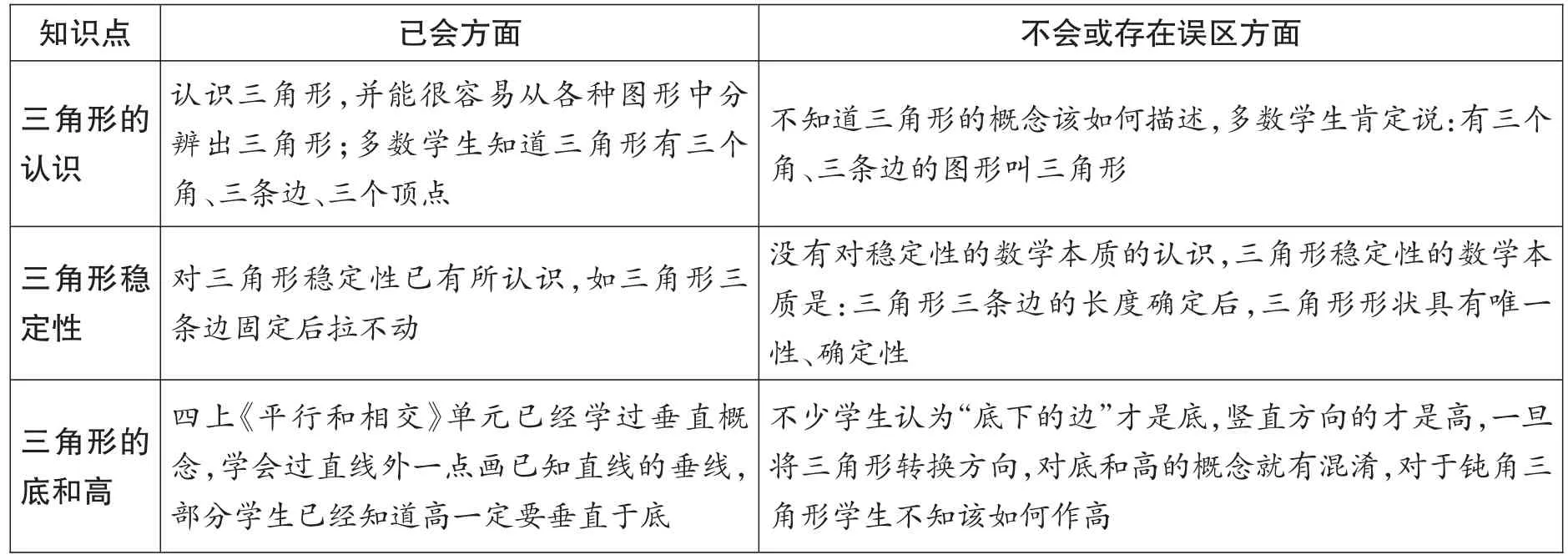
表1 对学生“三角形”知识的学情分析

通过学情分析，笔者认为本单元的教学关键就是在上述儿童不会或不理解的方面取得突破。例如“三角形高”的教学，一方面要突破学生对底和高的认识误区，可以在认识典型底和高的基础上，用课件将三角形旋转，让学生判断原来的底和高现在是否还是三角形的底和高；另一方面在画高的指导上，要充分利用儿童的已有知识经验（两点之间的距离、两平行线之间的距离、点到直线的距离）对三角形高的画法进行探究，引导儿童思考这些距离有什么特点——最短与垂直。后一单元教学平行四边形、梯形高时要与三角形高进行比较，将三角形的高概括为“过直线外一点作已知直线的垂直线段”，即“顶点到对边的距离”，将平行四边形、梯形的高概括为“两条平行线之间的距离”等。由此凸显三角形、平行四边形与梯形高的数学本质。

2.暴露儿童的“原初思维”，是纠正迷思概念、相异构想的契机

传统教学中，一方面儿童不敢暴露自己的真实想法，怕回答不符合要求，惹人笑话；另一方面教师担心儿童的“奇谈怪论”会干扰教学预设，导致师生双方顾虑重重，本该生动活泼的课堂变得单调、呆板。教学中教师应创造更多暴露儿童“原初思维”的机会，并有意按儿童常见的、多发的思维歧路适当出错，然后分析错误类型。在此基础上引领儿童展开数学思考，让儿童分享彼此观点，进而识别、纠正迷思概念、相异构想，建立正确的数学概念。

教学国标苏教版小学数学四年级下册《因数与倍数》一课时，笔者先让学生从3、5、6、18、35这五个数中，选择两个说说谁是谁的因数，谁是谁的倍数。

师：如果我们把以上各个数所有的因数都写出来，估计一下，这五个数中哪个数的因数会最多？

生（异口同声）：35。

师：为什么？

生1：因为这么多数里面35最大。

师：大家都是这么认为的吗？

生（齐声）：是。

师：那是不是数越大，这个数的因数个数就越多？肯定吗？

学生经过列举统计，发现18的因数个数比35多。

师（小结）：看来并不是这个数越大，其因数就越多啊。

上述教学环节，儿童由原有的相异构想得出了错误结论。如果教师不去解决，这个想法还将存在。所以，教师必须为儿童提供暴露相异构想的机会，通过举例阐释，让儿童辨析判断，消除儿童对数学概念的曲解，进而准确地把握数学概念。

3.引发儿童的“认知冲突”，是纠正迷思概念、相异构想的关键

所谓“认知冲突”，就是儿童原有认知结构与新知之间的矛盾。儿童在学习新知时，总是试图用原有认知图式来同化“新知”。当遇到不能解释的新知时，就会引发认知冲突。教学中教师要设法给儿童一个“震颤”，动摇儿童迷思概念、相异构想的信念基础，并引领儿童反思，组织儿童讨论、争辩，最终揭露儿童迷思概念、相异构想的不合理性。

教学国标苏教版小学数学六年级上册《长方体和正方体》中“包装的学问”，儿童凭借生活经验，都认为不论包装怎样的物品（指长方体物体），包装多少盒，只要是用大面重叠的方法，就是最省包装纸的，因为重叠的面积越大，需要包装的面积就越小。笔者引导学生利用生活中的磁带、牙膏盒、牛奶箱等物品，亲自动手摆、量、算、比，之后儿童发现：如果包装1盒到3盒，一般用大面重叠的方法最省包装纸；如果包装4盒或4盒以上，就要分析、比较多种包装方案，从中选取最省包装纸的一种方案。因为研究对象不同，最省包装纸的方案也就不同。如包装4盒磁带是重叠6个大面的包装，最省包装纸；而包装4盒牙膏或4箱伊利牛奶，则是重叠4个大面、4个中面，比重叠6个大面更省包装纸。经过探究性实践，儿童检视自己头脑中原存的相异构想，对“如何拼接长方体而节省包装材料”有了更为理性的认识。

4.发展儿童的“逻辑思辨力”，是纠正迷思概念、相异构想的保证

儿童逻辑思辨力的良好发展，是纠正迷思概念、相异构想的基础。首先，要培养儿童对于概念的细微分辨力。对于有微妙差别的数学概念，必须引领儿童分辨，例如“提高了”和“提高到”、“是甲的一倍”和“比甲大一倍”等。其次，教师组织儿童学习时，要有意识地将新知和儿童的迷思概念、相异构想联系起来进行揭示、比较、批驳，可采用变式，如学习“等腰三角形”，由于受标准图形的影响，儿童容易把“两边相等”这一本质特征误解为“左右两边相等”，这加深了“顶角在上，底角在下”的印象。教学时可以用多媒体将图形旋转（不同位置的呈现），将图形变形（不同形状的呈现——锐角等腰三角形、直角等腰三角形和钝角等腰三角形），从而让学生掌握等腰三角形“两边相等”的数学本质。再次，要重视培养儿童思维的严密性和全面性，让儿童不仅能进行“点”式、“线”式思维，而且能进行“面”式、“体”式思维。如教学面积单位要联系长度单位，教学体积单位要联系长度单位和面积单位等。再如教学“圆柱的体积”计算，笔者首先让学生整体感悟，建立一种上位认识：长方体、正方体、圆柱体的体积计算都可以用本质方法——“底面积×高”，然后让学生从圆柱体的本质方法出发，建构圆柱体体积计算的多元性方法（如，从整体把握局部。这种“整体感悟式”教学策略的运用，可以发展儿童的逻辑思辨力。▲

[1]于国海.相异构想与小学数学教学[J].现代中小学教育,2005(2)：46.

[2]郑毓信.数学思维与小学数学[M].南京：凤凰出版传媒集团江苏教育出版社，2008.

[3]杨淑娟.小学数学教学中相异构想初探[J].小学教学参考：数学版,2011(7)：9.

[4]仇正达.中学英语教学中相异构想的成因与纠正[J].江苏教育研究：理论版,2011（7）：46.

[5]吴荣安.基于学生经验的数学课堂资源开发与利用策略[J].江苏教育：小学教学版,2012(9)：36.