钢铁产业政策演进影响因素实证分析
张雅楠
摘要:本文运用主成分分析的方法,对选取的影响钢铁产业政策演进的6个主要的影响因素进行了实证分析。研究表明,对钢铁产业政策演进影响程度较大的影响因素分别为产业布局、产业结构、产业组织、产业技术创新4个因素。
关键词:钢铁产业;政策演进;影响因素
1.引言
我国政府为了实现一定的社会和经济目标,而对钢铁产业的形成和发展进行干预的各种政策的总和即为钢铁产业政策。“钢铁产业政策是以钢铁产业为直接对象,保护和扶植钢铁产业,调整和整顿钢铁产业组织,其目的是实现经济稳定与增长,改善资源配置,增强国际竞争力,改善与保护生态环境等。钢铁产业政策要求我国政府对每个钢铁企业的生产活动、交易活动都进行一定的干预,从而直接或间接地干预市场的形成和市场机制,进而实现特定的经济性的或社会性的目标[1]”。钢铁产业政策的演进是在一些影响因素的推动之下发生的。通过对现有文献和研究分析可以发现,钢铁产业政策的制定和实施会受到钢铁产业布局、钢铁产业组织、钢铁产业结构变动、钢铁产业技术创新、钢铁产能变化和钢铁产业环保这几种因素的影响。本文采用主成分分析法对这几种因素影响程度的大小进行了实证分析。
2.模型简介及数据选取
为定量判别影响因素对钢铁产业政策演进的影响因素,本文釆用主成分分析法来确定各因素对政策演进影响的方差的大小,进而通过建立综合评价模型确定各因素影响程度的大小,以确定钢铁产业政策演进过程中的主导影响因子。
“主成分分析法是设法将原来众多的具有一定相关性的各个指标重新组合成一组新的、互相无关的、综合指标来代替原来的指标,在数学上的处理就是,将原来P个指标作为线性组合,作为新的综合指标。最经典的做法就是用F1的方差来表达,即Var(F1)越大,表示F1包含的信息越多。因此在所有的线性组合中选取的F1应该是方差最大的,故称F1为第一主成分。如果第一主成分不足以代表原来P个指标的信息,再考虑选取F2,即选择第二个线性组合,为了有效地反映原来信息,F1已有的信息就不需要再出现在F2中,用数学语言表达就是要求Cov(F1,F2)=0,则称为第二主成分,依此类推可以构造出第三、第四,……,第P个主成分。
主成分分析数学模型如下:
F1=a11X1+a21X2+……+ap1XpF2=a12X1+a22X2+……+ap2Xp……Fm=a1mX1+a2mX2+……+apmXp
其中a1i,a2i,……,api(i=1……m)为X的协方差矩阵∑的特征值对应的特征向量,X1,X2,……,XP是原始变量经过标准化处理的值[2]”。
因为在实际应用中,存在着指标的量纲不同,为了在计算之前去除量纲的影响,就需要将原始的这些数据标准化,本论文中数据都是关于影响程度重要性的打分,不存在量纲影响,因此,不需要进行数据标准化。
本研究主要是根据主成分分析法进行因子分析,建立主成分得分系数矩阵,再建立综合评价模型,根据模型中变量系数确定权重,以确定影响度的大小。
根据前文对钢铁产业政策演进影响因素的研究,其影响因子主要选取了钢铁产业布局、钢铁产业组织、钢铁产业结构变动、钢铁产业技术创新、钢铁钢铁产能、钢铁产业环保这6个因素来分别代表模型中的变量X1-X6。
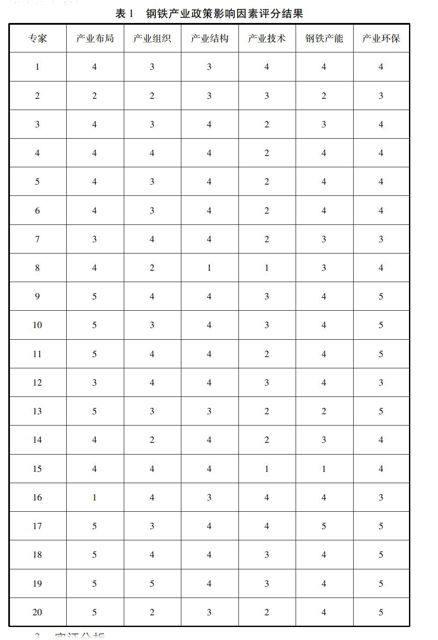
为保证分析结论的准确,邀请包括政府、企业、科研院校、在内的20名专家进行了影响程度调查。这些专家均长期从事对钢铁产业发展的研究,其中包括:河北省发展与改革委员会2人,首钢集团3人,唐钢集团5人,天津财经大学5人,江西师范大学5人。模型所需数据是根据专家对影响因子的影响程度大小打分获得,评分标准为:影响程度非常大5分,影响程度大4分,影响程度一般3分,影响程度不大1-2分。本次共向有关人员发放调查问卷20份,收回有效问卷20份,评分结果如下表:
3.实证分析
按照对专家的调查数据,结合因子分析法,对钢铁产业政策演进影响因素的因子分析如表2。
根据“KMO和Bartlett的检验”可知:巴特利特球度检验统计量的观测值为53.262,相应的概率值接近0,小于显著性水平0.05,故应拒绝原假设,认为相关
数矩阵与单位矩阵存在显著差异。Kaiser给出了常用的KMO度量标准:0.9以上表示非常适合;0.8表示适合;0.7表示一般;0.6表示不太适合;0.5以下表示极不适合。本模型KMO的值为0.837,0.837大于0.8,所以原有变量适合进行因子分析。
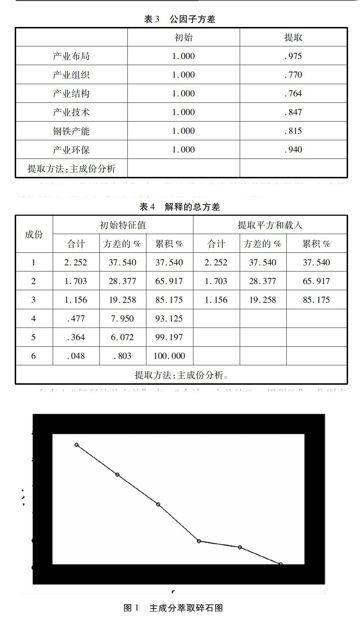
在表3“公因子方差”中,显示了这些变量的共同度数据。上表第一列是影响因子,第二列是因子分析初始解下的变量共同度,该列数据表明,如果对原有的6个变量釆用主成份分析方法提取所有的6个特征值,那么原有变量的所有方差都可被解释,变量的共同度都是1。实际上,因子个数小于原有变量的个数才是因子分析的目标,所以不可提取全部特征值[2]。上表第三列是按指定提取条件——即所有特征值都大于1——提取的特征值的共同度。从上表可以看到,除产业组织、产业结构和钢铁产能略小之外,其余的变量均在0.83以上。在表4“解释的总方差”中,“合计,方差的%,累积%”,分别表示特征值,方差贡献率,累计方差贡献率,它们描述了因子分析初始解的情况。可以看到,第一个因子的特征值为2.252,解释第一个变量方差的37.540%(即2.252/6*100%),累积方差贡献率为37.540%;第二个因子的特征值为1.703,解释第二个变量方差28.377%(即1.703/6*100%),累积方差贡献率为65.917%{即(2.252+1.703)/6*100%};第三个因子的特征值为1.156,解释第三个变量方差19.258%(即1.156/6*100%),累积方差贡献率为85.175%{即(2.252+1.703+1.156)/6*100%}。其余数据的含义与之类似。在第一列数据初始解中,由于提取了6個因子,因此原有的所有的变量的总方差均被解释,累积方差贡献率100%。
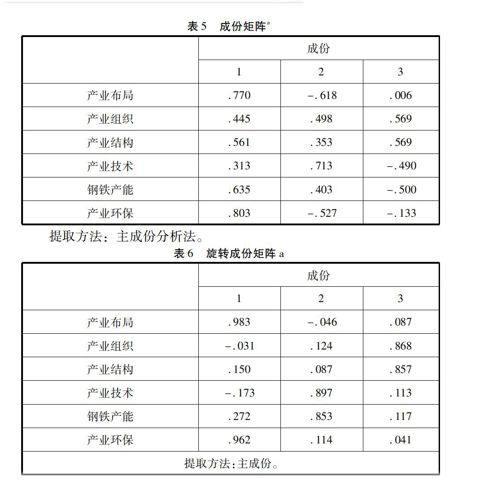
根据主成分萃取获得的碎石图(图1)可看出,成分1、2、3非常陡峭,4、5、6较为陆峭。但考虑到一般按照特征值大于1的规则确定主成分,由于成分1、2和3累积方差贡献率为85.175%,大于85%。因此,选择提取主成分数量为3。获得的成分矩阵、旋转成分矩阵、成分转换矩阵与成分得分系数矩阵、成分得分协方差矩阵见表5—表9。
4.实证结果
对提取的三个主成分得分系数矩阵进行分析,可以发现主成分一对产业布局、产业环保因素反应充分;主成分二对钢铁产业技术创新、钢铁产能、产业环保因素反应充分;主成分三对产业组织、产业结构因素反应充分。
利用主成分得分系数中的数据得到的三个主成分模型如下:
F1=0.493X1-0.081X2+0.12X3-0.124X4+0.103X5+0.481X6F2=-0.076X1-0.059X2-0.88X3+0.597X4+0.553X5+0.041X6F3=-0.001X1+0.598X2+0.583X3-0.057X4-0.079X5-0.059X6
用第一式F1中的每个变量所对应的系数乘上第一主成份F1所对应的贡献率37.540%,再除以所提取三个主成份的三个贡献率之和85.175%,然后加上第二式F2中每个变量所对应的系数乘上第二主成份F2所对应的贡献率28.377%,再除以所提取三个主成份的三个贡献率之和85.175%,然后加上第三式F3中每个变量所对应的系数乘上第三主成份F3所对应的贡献率19.258%,再除以所提取三个主成份的三个贡献率之和85.175%,就可得到影响因素綜合得分模型[2]:
Y=0.191879X1+0.07978X2+0.125457X3-0.03527X4-0.54104X5-0.13012X6
从综合得分模型来看,各因子对钢铁产业政策演进影响程度从大到小分别为钢铁产业布局、钢铁产业结构、钢铁产业组织、钢铁产业技术创新、钢铁产业环保和钢铁产能。
从中我们选取对钢铁产业政策演进影响程度较大的钢铁产业布局、钢铁产业结构、钢铁产业组织、钢铁产业技术创新这4个因素为主导因子。(作者单位:江西师范大学财政金融学院)
参考文献:
[1][日]长谷川启之,梁小民,刘朝,经济政策的理论基础:中国计划出版社,1995.
[2]杜强,贾丽艳,SPSS统计分析:人民邮电出版社,2014.07.
[3]仇兵奎.山西煤炭产业政策演进研究[D].(博士论文)华中科技大学,2013.

