先简支后连续T梁负弯矩区孔道横向偏位影响分析

丁 琦，王泽林

(湖南省高速公路管理局，湖南 长沙 410001)

0 前言

先简支后连续梁桥结构具有造价低、整体性好、建筑高度低、整体性好、桥面接缝少、行车舒适等优点，在当前施工中应用较广泛。但是，在施工过程中，由于施工人员的技术水平差异，加上操作不仔细，导致各种施工问题的发生，给后续运营过程中带来了不利影响。预应力孔道偏位作为其中一种典型问题，在施工中时有发生，但往往重视程度不足。分析表明:该类病害带来的影响不可低估。通过对某高速公路桥梁实际施工过程中发现的横向偏位进行分析，得到了相关影响值，可为指导正确处理类似问题提供参考。

1 问题的提出

某桥为12 ×30 m 预应力混凝土连续T 梁，先简支后结构连续，设墩顶现浇连续段和负弯矩钢束，每4 跨为一联，共3 联，每跨5 片T 梁，负弯矩区共设4个预应力孔道。在施工过程中，发现某联3#墩墩顶3#梁两纵向相邻梁顶部负弯矩预应力孔道横向偏位，偏差值分别为 38、50、43、45 mm，见图1。规范允许偏差10 mm(《公路桥梁施工技术规范》JTG/T F50—2011 第7.8.1 条后张预应力管道安装允许偏差同排为10 mm)，超过规范允许值。当即引起了建设部门的高度重视，需对问题作定性和定量分析。

图1 墩顶负弯矩区预应力孔道偏位

2 模型的建立

采用桥梁专业计算软件MIDAS 对该联4 跨连续T 梁建立有限元模型(图2)。边界条件和施工阶段按照实际情况进行模拟，并在模型中做如下处理:

图2 连续T 梁模型

1)为量化分析偏位的影响，分别计算负弯矩区钢束无偏位和有偏位情况，偏位值按实际偏差值进行模拟。见图3、图4。

2)荷载考虑恒载(包括主梁自重、横隔板、湿接缝和二期恒载)、温度荷载、汽车，并考虑汽车的冲击效应。

并在计算中作如下假定:

1)受力过程中，截面为平面;

2)预应力筋为线弹性材料，即应力与应变成正比关系;

3)T 梁的承载能力计算中，拉力由预应力筋承担，不考虑混凝土与普通钢筋的影响。

图3 无偏位预应力束模型

图4 偏位预应力束模型

由于问题的发生是在架梁完成时，为定量分析偏位对施工阶段的影响，通过单元、荷载、边界条件的钝化与激活建立施工阶段，具体分成如下4 个阶段:

1)预制T 梁，张拉正弯矩预应力束;

2)架梁，浇筑横向连接;

3)浇筑墩顶现浇段，张拉负弯矩区钢束;

4)拆除临时支座，体系转换，二期铺装及护栏施工。

3 荷载及组合

3.1 荷载

1)恒载:包括主梁、横隔板、湿接缝和二期恒载均按混凝土的容重选取，即26 kN/m3。

2)预应力荷载:预应力筋根据设计选取。

3)温度荷载:结构整体升温34 ℃，整体降温－3 ℃。

3.2 组合

根据规范的要求，Midas 自动进行荷载组合，主要包括以下组合。

1)承载能力极限状态:组合设计值=1.2 ×永久作用+1.4 ×汽车荷载+0.8 ×1.4 温度作用。

2)正常使用极限状态:

作用短期效应组合:永久作用+0.7 ×汽车荷载+0.8 ×温度作用(含温度梯度);

作用长期效应组合:永久作用+0.4 ×汽车+0.8 ×温度作用(含温度梯度)。

4 计算结果分析

4.1 钢束产生的内力值

负弯矩区钢束张拉后、体系转换施加二期恒载后，墩顶处钢束产生的内力值见表1。

表1 墩顶处钢束内力值 kN·m

在张拉至体系转换、二期铺装施工后，因钢束偏位，钢束产生的内力值在每个阶段均有降低。且变化值基本相同。表明钢束偏位后，对每个阶段的内力值均有影响，并且使内力值减小。由此可推断将产生预应力损失。

4.2 对结构承载能力的影响

4.2.1 开裂弯矩

1)消压弯矩计算:

当梁截面承受的弯矩等于消压弯矩时，梁截面下边缘的应力应变为零，截面处于全截面受压状态，而全截面的合压力等于即为预应力束的压力，又根据预应力束内力平衡，即内力的大小等于预拉力的大小，则有:

式中:Fc为全截面的合压力;Fp为预应力束的预拉力。

此时，截面上的压应力分布近似为三角形，由此可以根据面积矩平衡确定合压力的作用点。则负弯矩截面合压力与预应力筋预压应力之间的距离为0.6h。则消压弯矩为:

2)非预应力受弯构件的开裂弯矩:

开裂前构件处于弹性状态，可以看成均质弹性体计算，根据求得的换算截面面积，求得受压区高度。

由平截面假定可知，破坏前，混凝土与预应力筋之间粘结良好，故可以按应变协调计算受力下的变形，可以将预应力筋与混凝土三种材料组成的截面换算成一种均质材料组成的截面承担。并且将混凝土的压应力近似地看作直线分布，即受压区的混凝土压力与平均应变成正比，同时，假定受拉钢筋水平位置处混凝土的平均拉应变与应力成正比。故可以得到消压后的组合截面受力图式如图5所示。

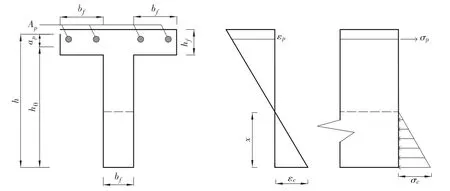
图5 消压后至破坏前组合截面受力情况

根据应变协调，有:

又由假设预应力筋在屈服前为线弹性材料，则有:

联立式(3)和式(5)代入式(4)可得:

其中αEpc=Ep/Ec称为组合构件截面中钢筋对混凝土的换算系数。则可以将钢筋面积换算成等效截面面积为:

可以得到换算后的等效截面如图6所示。

图6 换算截面

则可得组合截面的面积的大小为:

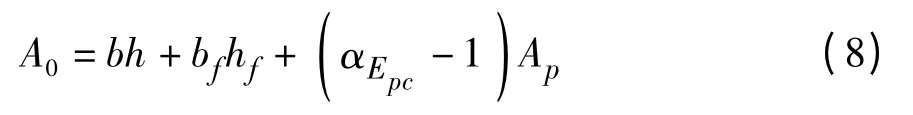
式中:b 为梁肋的宽度，该桥为0.2 m;h 为梁肋的高度，该桥为2 m;bf为翼缘板的宽度，该桥为0.9 m;hf为翼缘板的高度，该桥为0.19 m。

同时，可以根据拉、压区对中和轴的面积矩相等，并考虑受压钢筋的影响，可以求得中和轴的位置，并可以确定受压区的高度x。

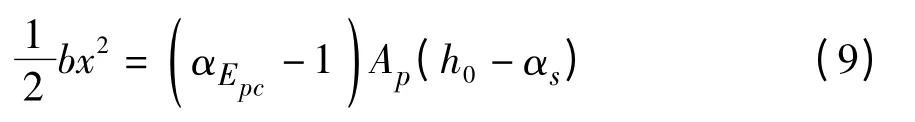
式中h0为有效高度，该桥为0.19 m。

从而解得受压区高度x 为:

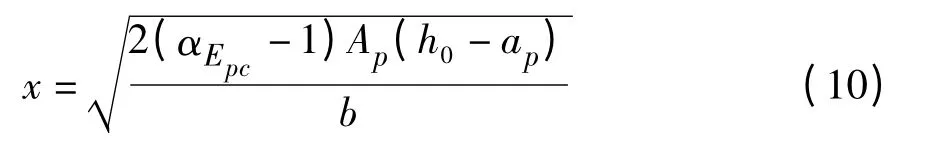
式中ap为受压区混凝土保护层的厚度。

由此可进一步解得组合截面的惯性矩为:

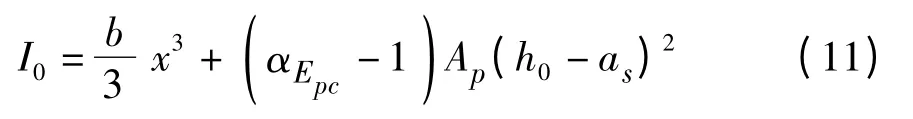
则受拉边缘的截面抵抗矩为:

由此可推得组合截面的开裂弯矩为:

式中:γm为截面抵抗矩塑性系数，γm=2S0/W0;S0为全截面换算截面重心轴以上(或以下)部分面积对重心轴的面积矩;ft为混凝土轴心的抗拉强度。

所以，构件的开裂弯矩为:

由此可求得钢束有无偏位时开裂弯矩值对比如表2。

表2 消压弯矩与开裂弯矩对比 kN·m

4.2.2 对承载能力的影响

结构抗力可按预应力混凝土结构的抗力公式计算，但未考虑普通钢筋及混凝土的受力，则表达式简化为:

式中:fcd为混凝土的抗压强度设计值，该桥为22.4 MPa。

受压区高度x 由力平衡求得，即:

式中:Ap为预应力束的面积，由设计图纸知，该值为660 mm2。

将各值代入，由此求得负弯矩区的偏位和未偏位时抗力值均为－8 358 kN·m。

4.3 变形的影响

负弯矩区孔道偏位，预应力张拉时会导致梁体变形。墩顶负弯矩钢束张拉时，梁体横向局部变形最大为0.11 mm;体系转换时，梁体横向局部变形最大为0.24 mm。横向变形均小于1 mm，对梁体影响较小。

5 结论

根据负弯矩预应力孔道横向偏位情况，采用有限元模型计算分析，结果表明:

1)偏位对预应力束产生的内力值在开裂前的各阶段均有影响，且影响值基本相同，表明产生的影响较稳定。在偏位值50 mm 以下，影响值不超过5%。

2)偏位对梁体的开裂值有影响，影响值不超过5%，对极限承载力无影响，对横向变形的影响几乎为0。

3)该T 梁负弯矩区预应力孔道偏位情况，可将孔道连接平顺，进行利用。在张拉过程中宜分级张拉，注意观测梁体变形及局部受力情况。

［1］刘小燕，颜东煌，张 峰，等.预应力高强混凝土梁极限承载力分析［J］.中国公路学报，2006(1):58 －61，79.

［2］郭 英.PC 梁预应力管道三维一体精确定位施工技术［J］.铁道建筑技术，2013(2):55 －58.

［3］陈美华.预应力混凝土先简支后连续T 梁的施工流程及质量控制要点分析［J］.城市道桥与防洪，2012(6):200 －204.

［4］周 俊，刘德朋，陈 浩.某公路大桥锚碇锚固系统预应力钢管精确定位［J］.施工技术，2005(7):57 －58，67.

［5］李克银，王亚平，等.有限元分析法在预应力砼T 梁验算中的应用［J］.交通科技，2004(4):9 －11.

［6］杨 勇.先简支后连续梁桥受力行为与施工技术研究［D］.重庆:重庆交通大学，2008.

［7］成 琛.大跨径PC 桥梁弯曲孔道有效预应力理论分析与试验研究［D］.武汉:武汉理工大学，2011.