斜T梁桥荷载横向分布系数实测与有限元分析

伍庆平

(湖南环达公路桥梁建设总公司，湖南 长沙 410004)

0 引言

我国修建的高速公路的中、小桥梁中，装配式T梁桥或现浇T 梁桥所占的比例很大，由于中小桥梁一般需配合路线设计，大量的中、小桥为斜桥。对于T 梁桥的活载弯矩计算，一般采用纵桥梁影响线，横桥向荷载分布系数的计算模式。利用内力或荷载的横向分布系数分析桥梁结构，实质上是在一定的误差范围内寻求一个近似的影响面来代替精确的影响面，把一个复杂的空间问题转化成平面问题来求解［1，2］。为确保桥梁结构在使用寿命期限内的安全性，设计过程中需准确计算各片梁所需承担的最大活载弯矩。荷载横向分布系数计算是公路桥梁设计中的重要内容。

荷载横向分布计算一直是公路桥梁设计中的一个重要内容。其定义是当把单位车道荷载按横向最不利位置布置在荷载横向影响线上，各片主梁在横向分配到的最大荷载的比例。目前，T 梁的常见荷载横向分布系数的分析方法［2，3］主要有:①杠杆法;②偏心压力法(修正偏心压力法);③铰接梁法;④刚接梁法等。杠杆法一般应用于计算荷载位于主梁支点处的横向分布系数，或者对于双主梁桥的荷载横向分布进行计算;偏心压力法适用于简支梁桥的中部，各主梁之间设置有可靠的中间横隔梁，且桥的宽跨比一般应小于等于0.5。铰接梁法适用于没有内横梁的小跨径简支T 形梁桥，主梁翼缘的连接构造较弱，现在实际工程中很少应用这样的桥梁。刚接梁法适用于翼缘板刚性连接的肋梁桥，也可适用于设置有中横隔板的桥梁。可以发现，这些理论方法有各自的适用范围，应按具体情况选用适当的方法来运用。但现有的横向分布系数的计算方法一般是基于直线桥梁得到，是否适用于斜梁桥值得进一步研究。对于斜梁桥只能采用上述方法对荷载横向分布系数进行估算，或者采用梁格法建立空间模型进行分析［4，5］，而梁格建模过程中横向单元的考虑方式对横向分布系数计算结果影响较大［6，7］。

基于此，本文首先对2 座斜交角分别为15°、35°的T 梁桥的荷载横向分布系数进行现场实测，再建立平面有限元模型对荷载横向分布系数进行计算，然后比较实测与理论分析结果，得出适用于斜梁桥的荷载横向分布系数简化分析方法。

1 荷载横向分布系数现场测试

1.1 工程概况

现场测试的2 座桥梁均位于高速公路上，其中桥梁1 为简支T 梁桥，斜交角为35°，跨径为25 m，桥梁1 截面尺寸及平面图分别如图1、图2所示。桥梁2 为3 ×40 m 装配式预应力混凝土连续 T 梁桥，施工方式为先简支后连续，斜交角为15°，桥梁2截面尺寸及平面图如图3、图4所示。2 座桥梁主梁均采用C50 混凝土，桥面宽度均为12.75 m，0.5 m防撞护栏+净－11.75 m 行车道+0.5 m 防撞护栏，桥梁设计荷载等级:公路－Ⅰ级。

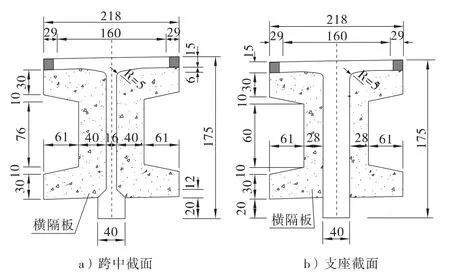
图1 25m斜交T 梁截面尺寸(单位:cm)

图2 25m斜交T 梁平面布置(单位:cm)

图3 40m斜交T 梁截面尺寸(单位:cm)

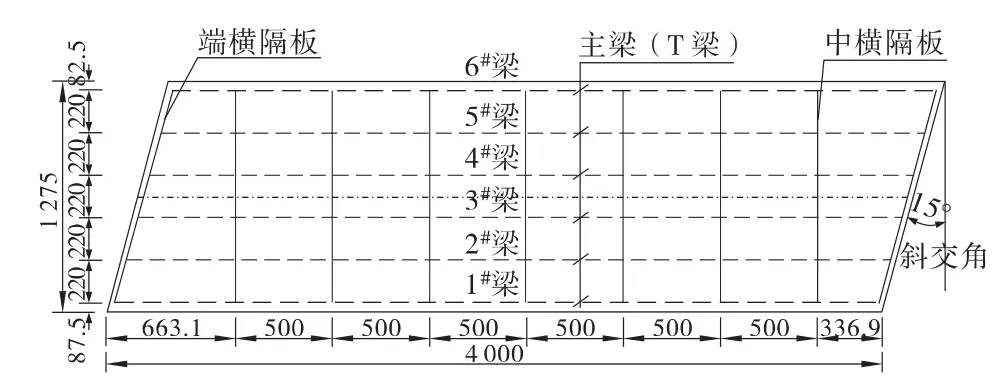
图4 40m斜交T 梁平面布置(单跨)(单位:cm)

1.2 现场测试工况

为检测桥梁的荷载横向分布系数，采用载重卡车集中加载的方式模拟汽车荷载，车辆吨位及数量根据相应控制截面内力的加载效率系数确定，所选卡车的重量为35 t，前轴重7 t，中轴及后轴重均为14 t。本文选取跨中正弯矩工况进行分析，通过计算发现，其中25 m 简支T 梁桥试验过程中跨中正弯矩工况所需车辆为5 台，3 ×40 m 连续 T 梁边跨最大正弯矩工况所需车辆为6 台。为求出边梁的最不利受力情况，分别对1 列车、2 列车、3 列车3 种工况进行荷载布置，各桥的工况如表1所示。加载布置分别如图5所示。2 座桥工况1、工况2 的布置方式一致，工况3 桥梁1 只增加1 台车，而桥梁2 增加2台车。

表1 各桥加载及测试工况

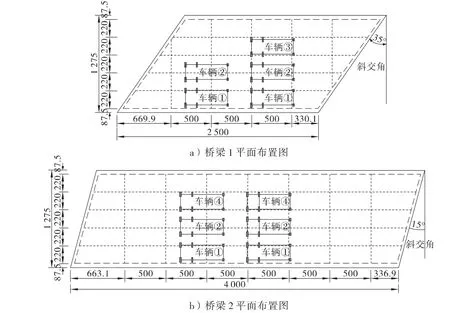
图5 加载布置图(单位:cm，待续)

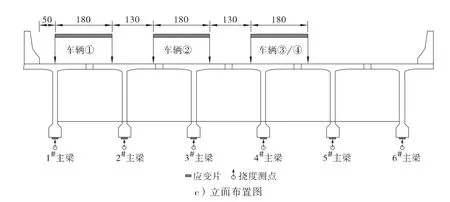
续图5 加载布置图(单位:cm)

荷载横向分布系数一般通过内力、挠度的横向分布规律来反映，因此加载过程中对各主梁的应力及挠度进行测试。应力通过黏贴在主梁下缘的应变片进行测试，而挠度通过在主梁下采用垂线法布置百分表进行测试。

1.3 现场测试结果

内力及挠度得到的边梁横向分布系数分别按式(1)、式(2)进行计算［8］，通过比较如图5c所示的 1列车、2 列车、3 列车得出的横向分布系数，取其最大值为边梁的荷载横向分布系数。

式中:mM、mf分别为内力及挠度得到的荷载横向分布系数;Wi、Ii分别为主梁截面抵抗矩(下缘)、惯性矩;fi为加载过程第i 片梁的实测挠度;εi为加载过程第i 片梁的实测下缘应变;n 为主梁数量;N为布置的车道数。主梁1 为边主梁，各主梁位置如图2或图4所示。

以桥梁1 为例说明各工况下应力及挠度测试结果。应变测试结果如图6所示，挠度测试结果如图7所示。表2为桥梁1、2 各工况下得到的横向分布系数。可以发现，2 座桥梁均是在布置3 列车时计算得到的横向分布系数最大。基于应变及挠度得到的桥梁 1 的边梁横向分布系数分别为 0.759、0.761，两者差值为1%。基于应变及挠度得到的桥梁2 的边梁横向分布系数分别为0.757、0.732，两者差值为3.4%。可以发现由应变得到的横向分布系数与由挠度得到的横向分布系数基本一致。

图6 桥梁1 应变实测结果

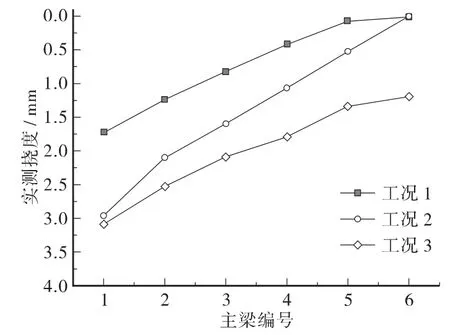
图7 桥梁1 挠度实测结果

表2 各工况下荷载横向分布系数

2 有限元分析

2.1 模型建立

由材料力学相关知识可知，板在跨中的挠度及转角可分别按式(3)、式(4)计算［2］:

上式中:E、G 分别为结构材料的弹性模量及剪力模量;I、IT分别为各主梁的抗弯惯矩及抗扭惯矩;b、l 分别为主梁宽度及跨径;p、mT分别为竖向荷载及扭矩。沿桥梁横断面取单位长度进行分析，可建立横向分布系数有限元模型，有限元模型如图8所示。

通过在各主梁位置模拟竖向等代弹簧及抗扭弹簧来模拟计算桥梁的竖向挠度及转角。［2］，考虑斜交角影响后，各主梁的竖向弹簧支撑刚度kw及扭转弹簧支撑刚度kφ分别如式(5)、式(6)。

上式中:di为各片主梁的中横隔板至梁端支点的距离，当di小于桥梁跨径一半时式(7)取“－”，大于时取“+”;Bi为各主梁至桥梁中线的距离;E =34 500 MPa，G=0.4E =13 800 MPa，考虑混凝土调平层(8 cm)影响后，桥梁1 的截面I、IT分别为0.311 m4、0.016 1 m4，桥梁 2 的截面 I、IT分别为 0.762 m4、0.017 2 m4。

图8 有限元计算模型

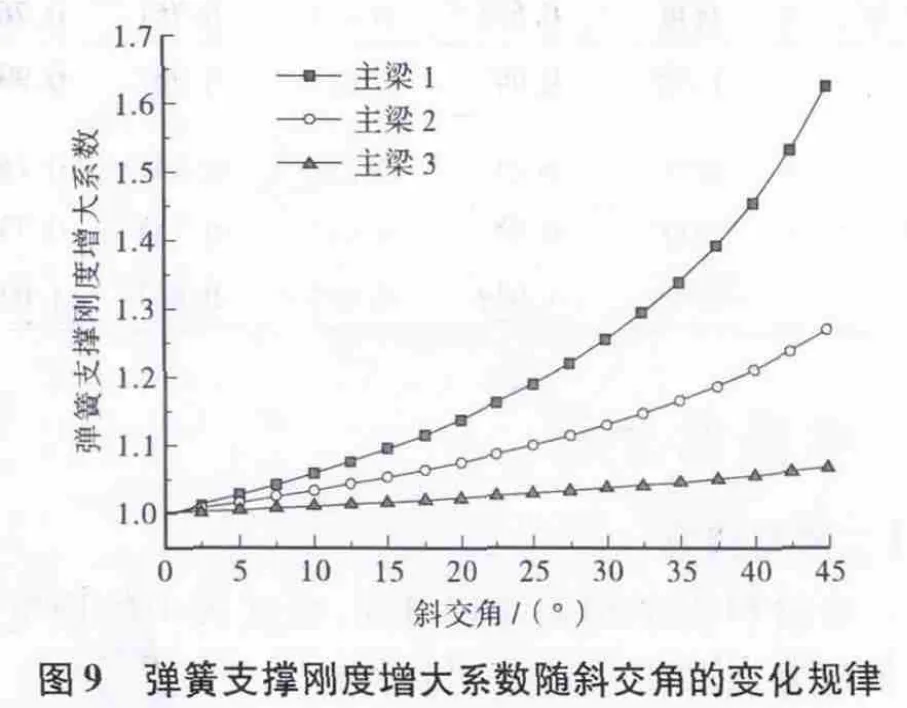
由表3可知，对称主梁的竖向弹簧支撑刚度kw及扭转弹簧支撑刚度kφ一致。以斜交角为0°(直桥)为基准，斜交角增大时，kw及kφ的增大系数完全相同。图9为以桥梁1 的参数为基础，斜交角由0增大到45°时，弹簧支撑刚度增大系数的变化规律，可以发现，斜交角越大，弹簧支撑刚度越大，桥梁宽跨比约为0.5 时，斜交角45°时，边梁的支撑刚度增大62.5%。

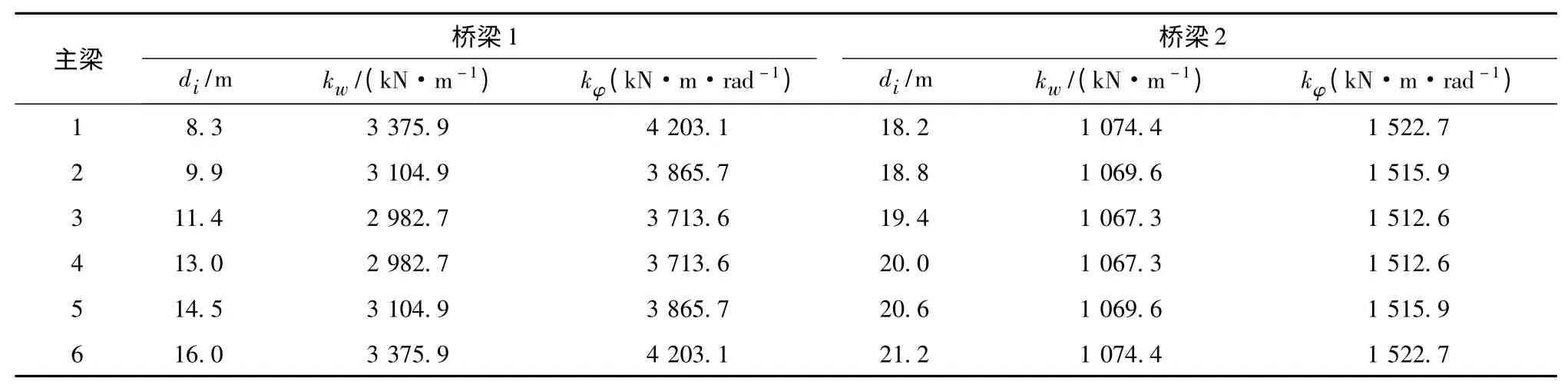
表3 各桥梁支撑刚度汇总表

2.2 计算结果

按照现行《通用规范》［9］的有关规定，对1 号边主梁进行最不利横向布置，在2.1 节所建立的有限元模型上进行荷载横向布置，直接输出i 号主梁下的弹簧支撑反力，支撑反力就是该号主梁的竖向荷载横向分布系数mρ，抗扭弹簧支撑的反力矩便是该号主梁的扭矩横向分布系数mT。桥梁1、桥梁2 的计算结果分别汇总于表4、表5。

由表4及表5可以发现，2 座桥梁的主梁1～3的竖向荷载横向分布系数均是工况3(也就是布置3列车)时最大，而主梁1～3 扭转荷载横向分布系数均是布置两列车时最大。说明对于斜桥，竖向荷载横向分布系数与扭转荷载横向分布系数加载工况可能不一致，需分开计算。另外，比较表4及表5可以发现，斜交角越大，边梁的竖向荷载横向分布系数越大。

表4 桥梁1 荷载横向分布系数汇总

表5 桥梁2 荷载横向分布系数汇总

3 试验结果与理论结果对比

为评估基于有限元模型计算荷载横向分布系数的可行性，本节将分析结果与实测结果进行对比，对比结果如表6所示。其中实测值按挠度结果得到，比较实测结果与有限元分析结果可以发现，桥梁1的误差为5.94%，桥梁2 的误差为4.07%。说明采用简化的有限元模型可较好地对斜桥荷载横向分布系数计算。

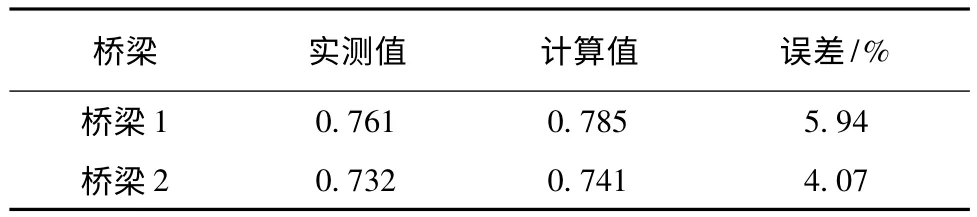
表6 荷载横向分布系数实测值与分析值对比

4 结论及建议

本文首先对2 座斜交角分别为15°、35°的连续T 梁桥的荷载横向分布系数进行现场实测，并采用平面有限元模型对荷载横向分布系数进行理论计算，通过现场及理论计算结果可以发现:

1)由应变得到的横向分布系数与由挠度得到的横向分布系数基本一致。

2)考虑斜交角的影响，通过在各主梁位置模拟竖向等代弹簧及抗扭弹簧来模拟计算桥梁的竖向挠度及转角，应用平面杆系有限元计算程序得到的横向分布系数模型可较好地计算荷载横向分布系数，而且对于斜桥，竖向荷载横向分布系数与扭转荷载横向分布系数布载方式可能不一致，需分开计算。

3)通过对2 座斜交桥梁进行现场测试并与有限元模型计算结果进行对比可以发现，最大差别为5.94%，说明采用简化的有限元模型可较好地进行斜桥荷载横向分布系数计算。

［1］刘 华，叶见曙，俞 博，等.桥梁荷载横向分布系数计算方法［J］.交通运输工程学报，2009，9(1):62 －66.

［2］邵旭东，翔 云，立 峰.桥梁设计与计算(第二版)［M］.北京:人民交通出版社，2012.

［3］宋建永，张浩阳，张树仁.公路桥梁荷载横向分布系数简化计算［J］.东北公路，2003，26(4):77 －79.

［4］黄平明，姚代禄.广义刚接梁 (板)法及对斜梁桥荷载横向分布的研究［J］.中国公路学报，1996，9(4):57 －64.

［5］江 甫.斜交角度对装配式钢筋混凝土简支斜交板桥的影响分析［D］.南京:南京航空航天大学，2006.

［6］余钱华，于 强.斜交空心板桥横向分布系数计算方法研究［J］.公路与汽运，2013 (3):171 －173.

［7］万 鹏，郑凯锋.组合有限元方法在T 形梁桥荷载横向分布分析中的应用［J］.公路，2003 (8):100 －105.

［8］程翔云，李新平.多格室曲线板桥荷载横向分布的简化分析［J］.中国公路学报，1989，3(8).

［9］JTG D60 －2004，公路桥梁设计通用规范［S］.