高速接触网导高偏差对弓网动态性能的影响
关金发,吴积钦,钟 源,张家玮
0 引言
接触线高度(下文简称导高)是指轨道平面与接触线下表面的垂直距离,是表征接触网重要的静态几何参数之一。导高偏差是指实际导高偏离接触网设计导高的差值,把实际导高比标称导高大的偏差称作负弛度,反之称作正弛度。几乎所有接触网机械结构均影响导高,如:基础、支柱、支持结构、定位结构、补偿结构、接触悬挂等,一旦其中一个或多个结构改变,最终均反映在导高上,引起导高偏差。
弓网动态性能的好坏取决于接触网与受电弓2个振动子系统的机械结构,接触网是受电弓的滑道,滑道的平顺性是保障良好弓网受流的前提,而滑道的平顺性主要取决于接触网静态几何参数,包括:接触线高度、接触线拉出值、接触线坡度等。高速铁路接触网对导高偏差的要求尤其苛刻。
文献[1~5]讨论了接触网几何参数偏差产生的 原因及提出减少偏差的措施。文献[6~10]讨论了弓网动态仿真模型的建立方法。文献[11]讨论了双弓对弓网动态性能的影响。文献[12,13]利用弓网仿真手段,优化了锚段关节的接触网模型。文献[14]结合现场安装的弓网监测设备,研究了接触网导高、弓网燃弧与弓网接触力的关系,得到弓网接触力幅度与接触线高度之间有一定的数量关系,以及验证了弓网接触力能同步反映出弓网离线的规律。文献[15]利用仿真手段,分析了吊弦缺失引起的接触网静态几何参数偏差对弓网动态性能的影响,并通过小波变化识别接触力缺失的波形,得出吊弦缺失与弓网动态接触力之间的关系。
综上所述,大部分文献研究的是如何减少接触网几何偏差,如何建立弓网模型进行弓网仿真,如何根据现场实测数据确认弓网仿真,但较少进一步阐述接触网的静态几何参数偏差对弓网动态性能的影响。本文研究导高偏差对弓网动态性能的变化规律,以吊弦长度、定位点高度变化为变量,对比不同参数下的弓网动态性能,得出导高偏差的最大合理取值,为接触网结构优化和接触线高度维修调整提供理论依据。
1 引起接触线高度变化的因素
接触线高度变化指的是接触线实际值与标准值的差值,可分为随机偏差、系统偏差、粗放偏差。在接触网施工、运营、维护过程中,由于零部件的安装调整不当,以及装置结构变形等都会使接触网静态几何参数出现与设计方案不同的偏差,这些因素反映到接触线的空间位置上,使接触线高度和横向偏移出现偏差,可能影响导高的原因有:张力补偿器误差过大;支持结构变形过大;结构部件与吊弦等产生松、断、脱;施工预配偏差过大;施工安装偏差过大;接触线磨耗过大;附加负载过大;轨道垂直不平顺过大。
吊弦对接触网静态形状的影响尤为重要,实际上由于现场安装或运行条件等多种原因,吊弦的长度总是与接触网设计值存在一定的偏差,而且不仅仅是单根吊弦出现偏差,很有可能全部吊弦高度均有偏差。
定位点的高度变化是影响接触线高度的关键因素之一,在速度大于250 km/h 等级时,标准要求两定位点的偏差为0,即不产生坡度,但在实际施工中很难保证,误差的产生是必然的。
2 弓网动态性能评价及弓网模型建立
弓网仿真的关键是得到弓网接触力,而其评价标准可根据EN50119:2001、EN50367:2006 和UIC799:2002,具体参数如下:
(1)平均接触力目标值(Ft):
Ft= 0.000 9 v2+ 70;
(2)最大标准差(σmax):σmax<0.3Ft;
(3)最大允许动态接触力(Fmax):
Fmax= Fm+ 3σ<350 N(速度大于230 km/h);
(4)最小允许动态接触力(Fmin):
Fmin= Fm- 3σ>0;
(5)实际接触力范围:0<F<350 N;
(6)定位点最大抬升量(dup):dup≤120 mm;
(7)受电弓最大垂向运动幅度(Δz):Δz≤ 80 mm;
(8)允许实际燃弧率(NQ):NQ≤0.2%。
接触网的核心部分是接触悬挂,在考虑建立接触网有限元模型前,首先假设支柱、支持装置是完全固定的,即忽略支柱、支持装置对接触网的影响。只研究定位装置、接触悬挂的有限元模型。
由于接触线和承力索的抗拉强度很小,索与梁单元的波动传播速度相当,基于以上考虑本文接触线、承力索单元均采用索单元。吊弦由于弓网接触力的作用会产生拉紧和松弛2 种状态,需要利用一个变刚度非线性单元。接触线、承力索、吊弦、定位点均采用一致质量单元。
通过坐标转换,把单元局部坐标系转换成整体绝对坐标系,组合单元质量矩阵与刚度矩阵形成接触网整体有限元模型:
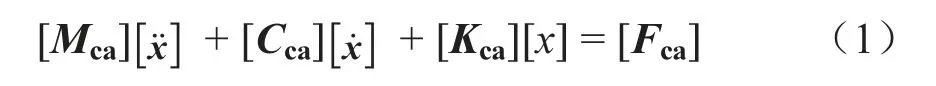
外力矩阵[Fca]考虑总的外载荷,每个时间步时间积分是均重新评估。假设t + Δt 时刻外力矩阵为
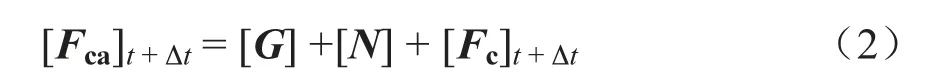
其中矩阵[G]、[N]分别为施加于接触网的重力和张力,这2 个外部载荷并不随时间改变,是一个常量。矩阵[Fc]为弓网接触力,其作用在接触线上的位置是随时间改变的。
受电弓一般使用集中质量模型,可分为两质量块、三质量块、多质量块模型。以两质量块模型作为分析对象,受电弓的动力学方程见式(3),可记为式(4)。
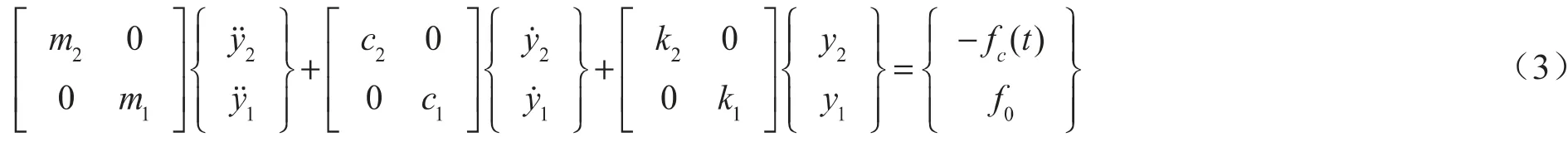
式中,fc为弓网接触力,N;f0为抬升力,N;kc为弓网接触刚度,N/m。
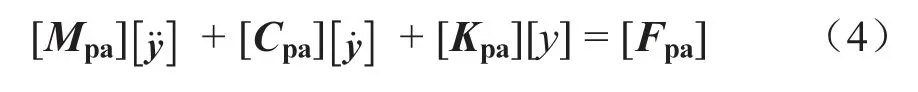
弓网相互作用关键是解决弓网接触问题,实际上弓网是一个滑动接触,在滑动的过程中伴随着离线的可能,利用Newmark-β 积分法,把时间离散成一个一个时间步,所以受电弓也可等效为一个时间步内向前移动一定距离,受电弓的移动速度与时间步的大小有关。
一般解决接触问题的方法是利用罚函数,令接触线单元i-j 与质量点m3的垂直方向位移为Δk,假设质量点m3在单元i-j 上方位移Δk 为正值,此时为接触渗透状态,反之质量点m3在单元i-j 下方位移Δk 为负值,见图1。
根据每个时间步Δk 的符号判断受电弓与接触线的接触状态,再根据接触刚度与Δk 的乘积作为分别作用于接触线和受电弓弓头质点的接触力,重新计算下一时间步接触网和受电弓的外部载荷产生的位移,如此反复,即可计算弓网相互作用。接触力计算公式为
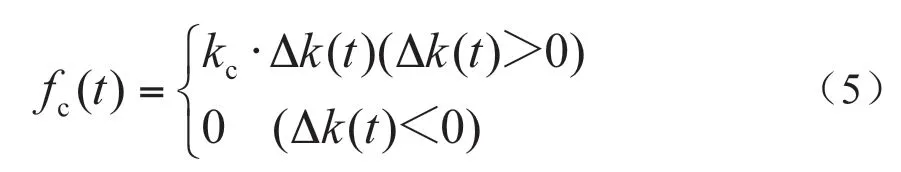
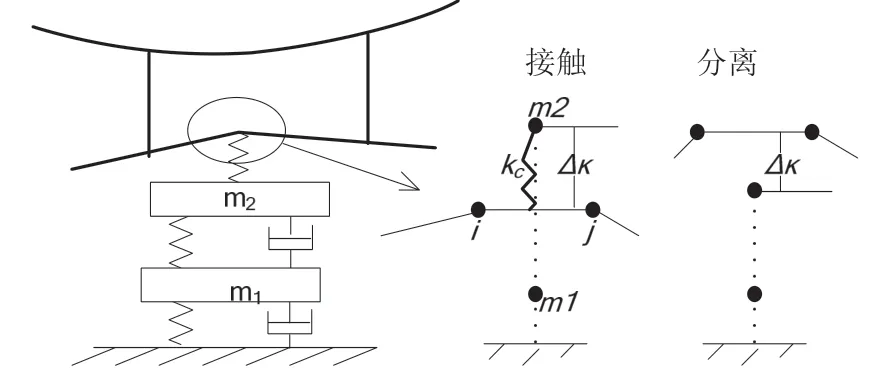
图1 弓网相互作用模型示意图
联合式(1)、式(4),列写统一的弓网动力学方程:
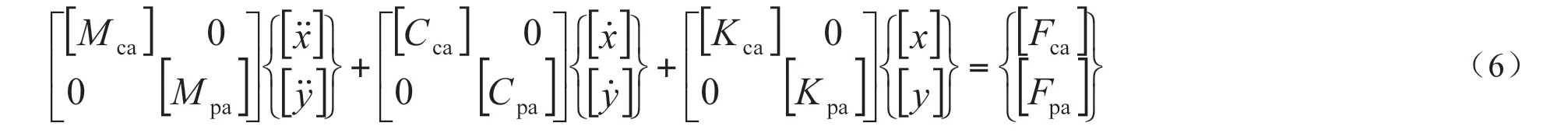
使用Newmark-β 积分算法求解式(6)。这里不详细推导,可参考有关数值积分方法的书籍。
研究对象为EN50318 中提供的弓网模型,利用上述讨论得到的弓网动态性能参数见表1,对照标准验证模型的正确性。
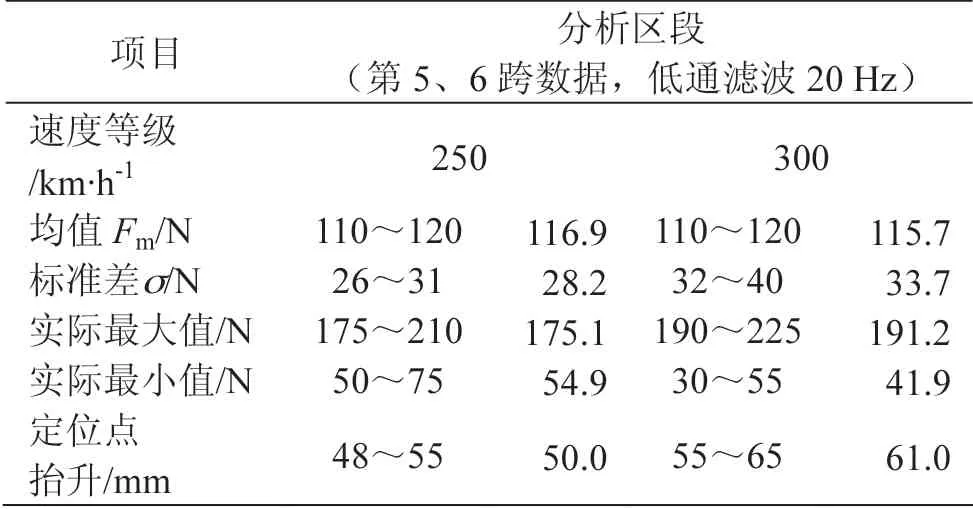
表1 弓网动态互相作用参数表
3 吊弦长度变化引起导高偏差
吊弦长度变化会使导高产生正负弛度偏差,下面研究单根吊弦引起导高正负弛度偏差对弓网动态性能的影响。
假设离跨中附近选择1 根吊弦,减少该吊弦长度,使接触线出现12、11、10、9、8 mm 的负弛度,其接触线静态平衡形状见图2。
利用第2 节方法进行弓网动态仿真,运行速度为300 km/h。由于接触线只在一点出现负弛度,受电弓在通过该点后,经过一定缓冲时间就能再次达到正常的运行轨迹,在接触力的统计区间,应选择受电弓弓头偏移正常轨迹的一段进行分析,见图3。
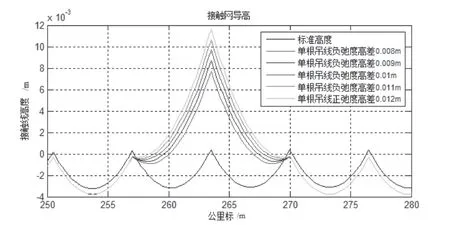
图2 单根吊弦负弛度接触线静态形状曲线图
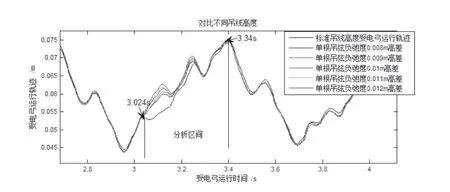
图3 单根吊弦负弛度受电弓通过前后运行轨迹曲线图
从图3中可以找出受电弓偏离标准接触网的大致区间,选择该区间为受电弓运行时间[3.024 s,3.34 s]内经过的接触网区域作为弓网接触力的统计区域。由于受电弓的运行速度为300 km/h,即统计的接触力区域为[257 m,278 m],20 m 的接触网区段。经过20 Hz 低通滤波后的接触力波形见图4,接触力统计值见表2。
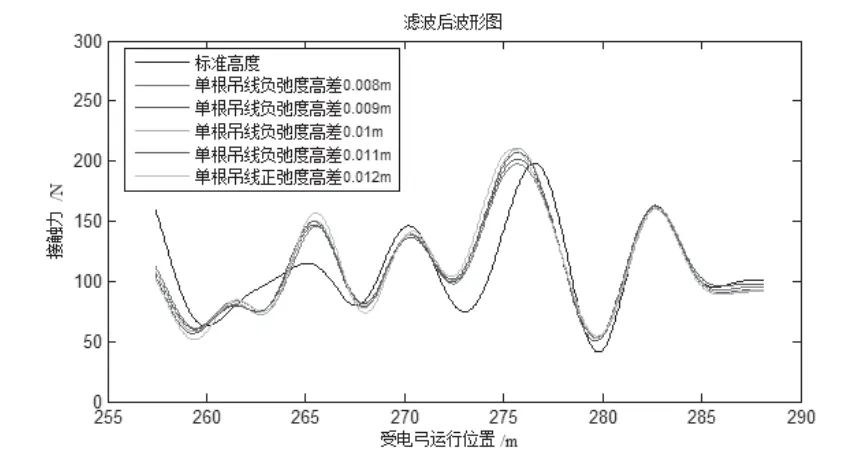
图4 单根吊弦负弛度分析区段弓网接触力波形图
观察表2中12、11、10 mm 偏差的最小允许动态接触力均小于0,即这3 种情况不满足弓网动态要求,而且随着负弛度偏差的增加,弓网接触力标准差也在不断增加,说明弓网接触力的波动越来越剧烈,当出现单根吊弦长度减少时,接触线的最大负弛度不应超过9 mm。
接触线存在正弛度现象,就像平直的路中出现了“凸起”一样,当受电弓通过该处时会造成弓头抬升突然减小,增加接触网与受电弓的振动,下文分析单根吊弦出现正弛度情况时,弓网动态性能的改变情况。
假设离跨中附近选择一根吊弦,增加该吊弦长度,使接触线出现14、12、10、8 mm 的正弛度,其接触线静态平衡形状见图5。

表2 单根吊弦负弛度分析区段弓网接触力统计值表

图5 单根吊弦正弛度接触线静态形状图
利用第2 节方法进行弓网动态仿真,运行速度为300 km/h,受电弓的运行轨迹见图6。分析区域与导高负弛度相同。经过20 Hz 低通滤波后的接触力波形见图7,接触力统计值见表3。
观察表3中14 mm 偏差的最小允许动态接触力小于0,12 mm 偏差的最小允许动态接触力接近0,即说明这2 种情况不满足弓网动态要求,而且随着正弛度偏差的增加,弓网接触力标准差也在不断增加,说明弓网接触力的波动越来越剧烈。综合以上分析,得出当出现单根吊弦长度增加时,接触线的最大正弛度不应超过12 mm。
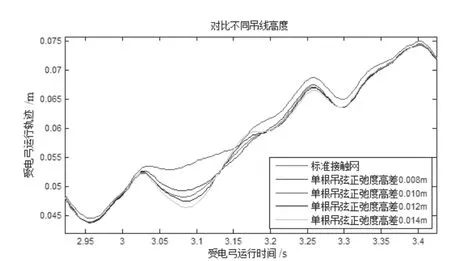
图6 单根吊弦正弛度受电弓运行轨迹图
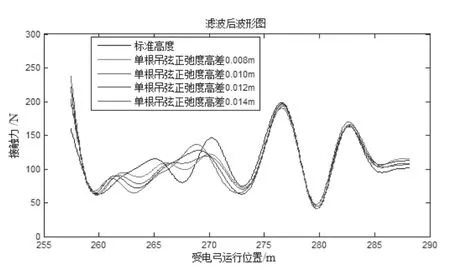
图7 单根吊弦正弛度分析区段弓网接触力波形图

表3 单根吊弦正弛度分析区段弓网接触力统计值表
4 定位点高度变化引起导高偏差
定位点高度受支持装置、定位装置、拉出值、第一吊弦位置及长度等影响,相邻定位点高度差与跨距之比为接触线坡度,标准中规定当速度大于250 km/h 时,接触线坡度的设计值为0,
定位点高度变化是影响接触网相邻定位点坡度的主要参数之一,相邻定位点坡度的定义为2 个定位点的高度差比跨距长度,若相邻定位点的相对标称接触线高度差±5、±15、±20、±30 mm 为研究对象,其相对的定位点坡度分别为0.17‰、0.5‰、0.67‰、1‰,具体接触线导高见图8。受电弓运行轨迹见图9。
从图9可以看出,随着坡度的增加,受电弓偏离标准受电弓运行轨迹的趋势更明显,受电弓的垂向运行幅度在不断增大。对比图8、图9,把受电弓运行时间换算成对应公里标,发现当受电弓通过接触线标称高度时,所有工况的受电弓运行轨迹从聚合到一点到再次分离。接触力统计区域见图9中分析区段1、2。由于分离方向的不同,有些受电弓运行轨迹往上移,有些受电弓运行轨迹往下移,故分别选择两个区域。接触力统计值见表4和表5。
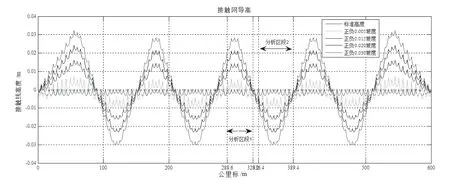
图8 同定位点高度的接触线静态形状图
从表5发现在定位点高度变化在±30 mm 的情况最小允许动态接触力小于0,说明该工况的弓网动态性能不符合标准,故定位点的最大偏差不应大于±20 mm,即坡度小于0.67‰。

表4 分析区域1 弓网接触力统计值表

表5 分析区域2 弓网接触力统计值
5 结论
接触网导高偏差的产生是不可避免的,影响导高偏差的主要原因有吊弦长度和定位点高度变化。
单根吊弦的高度变化不足以影响相邻定位点的抬升,但是随着负弛度或正弛度偏差的增加,弓网接触力标准差不断增加,表示弓网接触力的波动越来越剧烈,通过仿真分析得出:300 km/h 运行速度下,当接触线出现单根吊弦负弛度时,最大偏差不应超过9 mm;当接触线出现单根吊弦正弛度时,最大偏差不应超过12 mm。
定位点的坡度越大,相邻定位点的抬升差值越大,通过对仿真结果分析得出:300 km/h 运行速度下,定位点的最大偏差不应大于±20 mm,即坡度小于0.67‰。
以上得到的接触网导高偏差的合理限值,为接触网导高验收和导高维修提供参考依据。
[1]陶立新.德国高速铁路接触网的施工允许偏差[J].电气化铁道,2000,(3):27-29.
[2]程德勤.接触线高度标准体系中的偏差技术[A].中国电气化铁路两万公里学术会议论文集[C].2005:109-114.
[3]杨湘民.浅谈接触网施工误差的控制方法[J].电气化铁道,2004,(1):15-17.
[4]张建红.控制接触网施工误差的方法探讨[J].科技与企业,2012,(23):188.
[5]罗忠.浅谈接触网施工误差的控制方法[J].西铁科技,2007,(S1):50-52.
[6]蔡成标,翟婉明.高速铁路受电弓-接触网系统动态性能仿真研究[J].铁道学报,1997,(5):38-43.
[7]周宁,张卫华.基于直接积分法的弓网耦合系统动态性能仿真分析[J].中国铁道科学,2008,(6):71-76.
[8]张卫华,曹新文.高速受电弓-接触网系统的动力学研究[J].西南交通大学学报,1991,(1):105-111.
[9]吴燕.高速受电弓-接触网动态性能及主动控制策略的研究[D].北京:北京交通大学,2011.
[10]赵飞.基于有限元的高速弓网系统动态性能仿真及分析[D].成都:西南交通大学电气工程学院,2012.
[11]吴燕.高速受电弓-接触网动态受流性能及双弓距离的研究[J].铁道学报,2010,(4):38-43.
[12]Jesus Benet.A Mathematical Model of the Pantograph- Catenary Dynamic Interaction with Several Contact Wires[J].International Journal of Applied Mathematics, 37:2.
[13]Jesus Benet.A mathematical study of the pantograph/ catenary dynamic interaction on transition spans[J].Proceedings of the World Congress on Engineering 2007 Vol II.
[14]Shunichi KUSUMI.Diagnosis of Overhead Contact Line based on Contact Force[J].Qr of RTRI, Vol.47.NO,1.
[15]A.Bobillot.Pantograph-Catenary three paths to knowledge[J].UIC 2006 第7 届世界铁道大会会议论文.

