基于变刚度弹簧模型的弓网动力学分析

吕青松，王世轩，周 宁，李瑞平，李红梅，张卫华

0 引言

受电弓-接触网系统为电气化列车运行提供能量，受电弓与接触网在滑动接触过程中完成取流，因此，弓网受流对列车运行的安全性和可靠性具有重要影响。弓网受流质量受到力学、机械、电气和材料等多种因素的影响，而弓网动力学性能对受流质量起到了决定性作用。干线铁路和高速铁路通常采用柔性悬挂接触网，而地铁线路通常修建于低净空隧道内，通常采用刚性悬挂接触网。国内外学者采用不同的建模和仿真技术对弓网耦合动力学仿真开展了深入研究。张卫华等利用Fourier 展开和模态技术，由第二类朗格朗日方程推导了柔性接触 网运动微分方程[1，2]。吴天行等计算了柔性接触网的静态刚度曲线，采用余弦函数拟合接触网刚度曲线从而建立了接触网简化模型，并将该模型应用于弓网耦合动力学仿真[3]。C.VERA 等建立了三维刚性接触网模型和多刚体受电弓模型，采用多体动力学软件分析了弓网动力学行为[4]。梅桂明等人通过弹性势能、动能相等的原理将刚性接触网悬挂机构简化为带有等效刚度和等效质量的弹簧，在此基础上建立了刚性悬挂接触网等效计算模型，利用假设模态法得到了刚性悬挂接触网的振动微分方程[5]。毕继红等人基于刚性接触网的等效模型，采用有限元法计算了接触网的固有频率和振型，然后采用振型叠加法对弓网耦合动力学进行了分析[6]。原华等人基于刚性接触网等效模型，采用有限元法建立了刚性接触网与受电弓的耦合动力学仿真方法[7]。然而，目前针对刚性接触网建立的弓网耦合动力学仿真方法，建模较为复杂，计算效率较低，因此，需要结合刚性接触网的应用条件以及弓网耦合动力学特性，提出更为简单和高效的仿真方法。文献[3]指出变刚度弹簧接触网模型由于无法考虑振动波在接触网中的传播，适用于低速时的弓网耦合动力学仿真，而刚性接触网通常应用于地铁线路，地铁车辆的运行速度一般低于120 km/h，因此，可采用变刚度弹簧模型模拟刚性接触网。本文基于刚性接触网等效模型，在此基础上提出一种更为简单的变刚度弹簧刚性接触网模型，将接触网表示成随着空间变化的刚度值，采用接触刚度模拟弓网之间的耦合行为，并将计算结果与采用有限元法获得的计算结果进行比较，验证文中所提方法的准确性，同时给出了2 种计算方法的使用范围；最后，对2 种方法计算所需时间以及模型复杂度进行比较，证明变刚度弹簧接触网模型在弓网耦合动力学仿真中具备一定的优势。

1 接触网-受电弓模型

1.1 刚性接触网等效模型

刚性接触网由接触线、汇流排及绝缘支撑装置等组成，如图1所示。刚性接触网的接触线固定在汇流排上，每隔一段距离使用特殊的夹具将其固定在隧道顶部。接触线与汇流排组成的结构自重大且无张力，可以将刚性接触网等效为由梁、带自重的弹簧组成的等效结构；根据静力平衡条件、动能和势能定理，获得悬挂机构的等效质量和等效刚度；汇流排与接触线可一起考虑成简支梁，从而得到刚性接触网的等效模型[5]，如图2所示。

图1 刚性接触网平面图

图2 刚性接触网等效模型示意图

1.2 刚性接触网数学模型

1.2.1 变刚度弹簧模型

刚性接触网变刚度弹簧模型是指将接触网考虑成空间上离散的刚度节点，刚度节点可通过刚性接触网等效模型计算获得或者通过线路试验获得，该模型忽略了振动波在接触网中的传播，可适用于低速时的弓网耦合动力学仿真。选取跨距为8 m，锚段长度为240 m 的刚性接触网为研究对象，通过数值仿真获得了接触网的静态刚度，如图3所示。由图可知，相比传统的柔性接触网，刚性接触网具有静态刚度大，悬挂机构处的静态刚度值远大于跨中处静态刚度值的特点。在弓网耦合动力学模型中，可将整个刚性接触网等效为刚度随受电弓运行位置而改变的变刚度弹簧，其刚度值由刚性接触网不同位置处的静态刚度确定，如图4所示。

图3 刚性接触网静态刚度曲线图

图4 刚性接触网变刚度模型示意图

刚性接触网变刚度弹簧模型中的弓网接触压力Fcp(t)可表示为

式中，ks为接触刚度；ycc为接触点处接触线垂向位移；ypc为接触点处受电弓垂向位移。

接触线垂向位移ycc可表示为

式中，k(xc)为弓网接触点处的静态刚度。

1.2.2 有限元模型

直接建模法采用有限元法对刚性接触网结构进行离散，得到刚性接触网的质量、阻尼和刚度矩阵，进一步得到接触网的微分方程：

式中，[Mc]，[Cc]和[Kc]分别为接触网的质量，阻尼和刚度矩阵；，和{yc}分别为接触网的加速度，速度和位移向量；{Pcp(x,t)}为t 时刻弓网接触压力向量。

1.3 受电弓模型

受电弓模型主要包括归算质量模型、多刚体模型、刚柔混合模型等。归算质量模型是对受电弓某个高度进行等效参数测试，从而将受电弓表示成集中质量、弹簧和阻尼相连的等效模型，如图5所示。归算质量模型具有自由度少、计算效率高的优点。

图5 受电弓质量块模型示意图

受电弓运动微分方程可表述为

式中，[Mp]，[Cp]和[Kp]分别为受电弓的质量，阻尼和刚度矩阵；，和{yp}分别为受电弓的加速度，速度和位移向量；{-Fcp(x,t)}为t 时刻弓网接触压力向量；{F0}为受电弓静态抬升力向量。

2 计算结果

2.1 接触压力

建立跨距为8 m，锚段长度为240 m 的刚性接触网等效模型以及SBS81 地铁受电弓归算质量模型。采用直接积分法对有限元模型进行弓网动力学仿真，以其计算结果验证本文提出的刚性接触网变刚度弹簧模型的准确性。按照同样的工况进行仿真，提取接触压力结果进行对比。图6为计算获得的不同速度条件下弓网接触压力时程，对比2 种方法的结果曲线发现，在速度120 km/h 以下，2 种计算方法的接触压力结果曲线吻合得很好。

图6 弓网耦合模型接触压力结果曲线图

参见图7，对于速度等级更高的工况进行计算后发现，在速度达到140 km/h 时，变刚度弹簧模型的接触压力产生了与刚性接触网模型接触压力之间较大的差异。提取各个速度等级接触压力结果的统计值对比后发现，速度在120 km/h 以下时，变刚度弹簧模型与有限元模型的统计值差异很小。速度工况100 km/h，2 种模型接触压力最大值相差1.46 N，最小值相差0.74 N，标准差相差 0.61 N。速度工况120 km/h，2 种模型接触压力最大值相差1.26 N，最小值相差0.09 N，标准差相差0.948 N。当速度达到140 km/h 以上时，变刚度弹簧模型与刚性接触网等效模型的接触压力统计值差异开始变大。速度工况140 km/h，2 种模型接触压力最大值相差8.30 N，最小值相差8.74 N，标准差相差 5.65 N，差异明显变大。因此变刚度弹簧模型的适用范围在低速区域，而现阶段刚性接触网主要应用于速度较低的线路条件，变刚度弹簧模型在现有工程应用中是足够的。当需要对速度等级较高的弓网动力学研究时，仍然应该使用有限元模型。

图7 接触压力统计结果对比曲线图

2.2 接触压力频谱

刚性接触网是以跨距为单位的周期性结构，因此，当列车以不同速度运行时，接触网对受电弓存在不同的跨距激励频率。频率值可用f= v / l 表示，其中，v 为运行速度。速度等级40、60、80、100 km/h时，对应的跨距频率分别为1.39、2.08、2.78、 3.47 Hz。对4 种速度条件下的接触压力分别做频谱分析，如图8所示，由图8可知，对弓网接触压力贡献最大的频率成分为跨距频率；同时由频谱结果可知，2 种方法计算获得的接触压力频谱特性也是一致的，从而进一步证明刚性接触网变刚度模型的计算结果是正确可靠的。

图8 接触压力频谱结果曲线图

2.3 计算效率

数值仿真的计算效率以及建模复杂程度对工程应用尤为重要。针对同一工况，统计文中2 种方法的计算耗时，以及对建模和编写程序的复杂度进行说明和比较。工况设定为列车运行速度80 km/h，列车运行时间5 s，仿真时间步长取0.001 s。图9给出了2 种方法进行弓网耦合动力学仿真时所需时间，由图可知，采用变刚度弹簧模型进行仿真时，计算效率很高，而使用直接积分法计算的有限元模型所需时间很长。因此，对于工程应用而言，从计算精度和计算效率上考虑，进行刚性接触网的弓网动力学仿真时，采用变刚度弹簧模型较为合适。

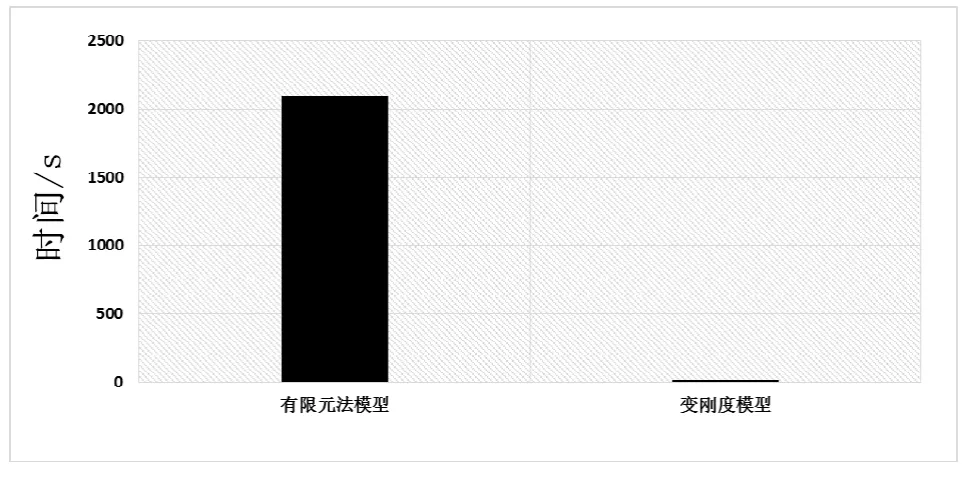
图9 计算时间对比图

刚性接触网有限元模型在接触网几何模型基础上，定义单元、单元属性、边界条件，划分网格获得有限元模型，建模过程复杂，计算时间长，适用于考虑复杂连接、过渡结构，如汇流排接头、锚段关节结构的动力学计算。变刚度弹簧模型根据刚性接触网的静态刚度直接建立弹簧模型，建模简单，方程求解微分项少，并且计算时间很短，适用于正常运营速度下的弓网动力学评价。

3 结语

本文提出了基于变刚度弹簧模型的刚性接触网-受电弓耦合动力学仿真方法，并与有限元的计算结果进行了比较，验证了该方法的准确性。

刚性接触网变刚度弹簧模型具有建模简单，计算效率高，适合地铁正常运营速度下的弓网动力学仿真和评价。

对于运行速度不超过120 km/h 的弓网动力学仿真计算，采用变刚度弹簧模型较为合适。而对于运行速度超过120 km/h 的弓网动力学仿真计算，采用刚性接触网等效模型进行计算则更为合理。

[1]W H Zhang, G M Mei, X J Wu.Hybrid simulation of dynamics for the pantograph-catenary system[J].Vehicle System Dynamics, 2002,38(6):393-414.

[2]W H Zhang, G M Mei, X J Wu, and L Q Chen.A study on dynamic behavior of pantographs by using hybrid simulation method[J].Rail and Rapid Transit,2005,219(3):189-199.

[3]T.X.WU, M.J.BRENNAN.Basic Analytical Study of Pantograph-catenary System Dynamics[J].Vehicle System Dynamics,1998,30(6):443-456.

[4]C.VERA, B.SUAREZ, J.PAULIN, P.RODRÍGUEZ.Simulation model for the study of overhead rail current collector systems dynamics focused on the design of a new conductor rail[J].Vehicle System Dynamics, 2006, 44(8):595-614.

[5]梅桂明，张卫华.刚性悬挂接触网动力学研究[J].铁道学报，2003，25（2）：24-29.

[6]毕继红，张峰，刘峰涛.刚性悬挂接触网/受电弓系统动力分析[J].沈阳理工大学学报，2007，26（4）：91-94.

[7]原华，毕继红，周全智.刚性悬挂接触网弓网耦合仿真研究[J].低温建筑技术，2007，116：51-53.