保险公司投资组合的最优化模型研究*

王乙娜，侯为波

(淮北师范大学数学科学学院，安徽淮北 235000)

1 保险投资的概述

定义1［1］保险投资是保险公司为了保证自己本身的赔偿能力，增大本身的竞争力，在经营业务的过程中，严格按照有关法律法规的要求运用积累的保险资金，使其维持增值保值的活动。

保险公司的利润主要是投资利润和承保利润。从国际保险业的承保大趋势来看，承保业务越来越多，承包责任越来越大。但是承保费率却越来越少甚至经常被压至成本之下，使得保险公司的承保业务盈利很少，有时会出现亏损现象，所以保险公司的利润主要来源于投资利润，故对保险公司的资金投资比例和最优化问题的研究尤为重要。主要是对于风险资产和无风险资产的投资组合进行了模型假设，使得在总收益和总风险达到一个最优化的状态而得到的最优解。

2 保险投资比例的理论模型

假设保险公司投资了M+1种资产，其中风险资产为M种，无风险资产为一种。设收集的保费为p0，无风险收益率为z，承保收益率为z0，第i种风险资产的投资收益率为zi，可投资资金的比例为t，bi为投向第i种风险资产的投资比例(0≤bi≤1)，bi为一个可控制变量，可被视为保险公司资产组合风险的一个变量，则保险公司的总收益为:

其中无风险资产的投资收益率z为确定的，因为保险赔付的随机性和投向第i种风险资产受市场风险的影响，所以承保收益率z0和第i种风险资产的投资收益率zi为随机变量。

因此保险公司的总收益(期望)和总风险(方差)为:

记b=(p0，tp0b1，tp0b2，…，tp0bM)T，

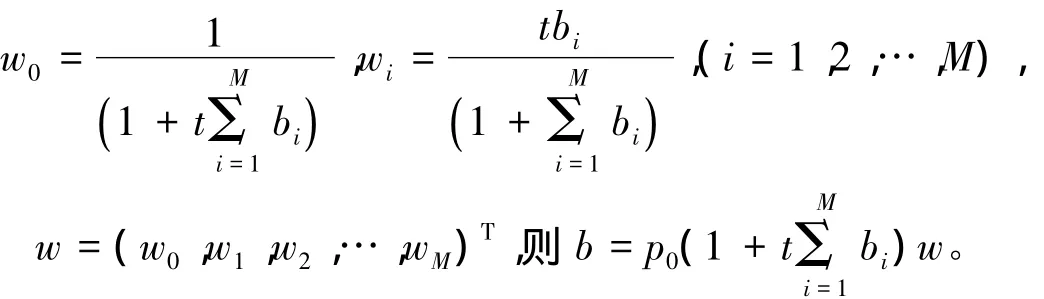
记Q=(1，1，…，1)T，Zs=(E(z0)+tz，(E(z1)-z)，(E(z2)-z)，…，(E(zM)-z))T，

其中 σii=Var(zi)，σij=Cov(zi，zj)，那么E(Z)=，Var(Z)=bTΩb。

无论任何一家保险公司，都希望总风险降到最低而总收益达到最高。因为总风险和总收益是成正比的，所以往往总收益越大总风险也就越大。保险公司在权衡总风险和总收益的基础上，用其对风险的偏好在无风险资产和风险资产之间进行组合，以求得到最大限度的总收益。这样既满足了保险赔付的需求，也能使总风险降到最低。所以在投资保险资产的同时，要兼顾风险和收益之间的关系，要建立最优单位风险的保险资金投资模型。要想求得保险公司的最优投资比例，建立最优化的投资模型，即求得模型的最优解w:

利用库恩—塔克条件来解这一非线性规划问题，解得最优化投资比例的最优解为:

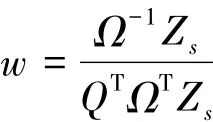
3 小结

这一最优解是在考虑了承保风险的情况下得到的，显而易见比把承保风险率看做是常数而不考虑承保风险的存在要科学的多。利用投资模型可以对我国大部分保险公司的无风险投资和风险投资的最优化组合得到初步的最优解。

［1］陈友平.论保险公司的投资策略［J］.保险研究，2000(7):79-101

［2］荣喜民，吴孟铎，刘泊炀.保险基金投资的单位风险收益最优化模型研究［J］.管理工程学报，2001，15(2):40-44