层次模型基本理论及其应用*

李 勇

(重庆工商大学数学与统计学院，重庆 400067)

在社会科学各领域中，常常会出现一些具有嵌套结构的数据类型。如在教育学中，学生组成班级，班级形成学校，学校汇成学区;在研究学生的情况时，可以涉及学生变量，同时可能考虑班级变量(包括学生变量的汇总，也包含班级自身变量)、学校变量和学区变量等。这就形成了从不同层级出发考虑同一问题的数据结构。这样的结构在很多领域都存在，如环境科学中的个体、种群和群落之间;经济学中的微观、中观和宏观;社会学中的个人、群体和全体;地理区划中的乡镇、区县、省市和国家等。可见具有嵌套结构的数据类型比比皆是。如何利用统计方法对这类层次结构数据进行分析?对这一问题的研究，形成了当前统计学科的一个热门领域——层次模型理论和方法。

1 基本模型

层次模型是一种基于层次结构所形成的数据所构成的一种统计模型。在不同的研究领域中名称不同:在生物统计领域，常称为混合效应模型(mixed-effects models)和随机效应模型(random-effects models，见Elston ＆ Grizzle，1962;Laird ＆ Ware，1982);在社会学领域，常称为层次模型(hierarchical linear models，见Lindley ＆ Smith，1972;Bryk ＆ Raudenbush，1992)和多水平模型(multilevel linear models，见 mason et al.，1983;Goldstein，1986);在计量经济学领域，称为随机系数回归模型(random-coefficient regression models，见Rosenberg，1973;Longford，1987);在统计学领域，称为协方差成分模型(covariance componentsmodels，见Dempster et al，1977)。

一般地，层次模型设为

其中，Y表示N×1响应向量;β表示p×1固定效应参数向量;X表示关于固定效应参数向量β的N×p解释性变量的设计矩阵;e(k)表示水平k下均值为0的随机误差;Z(k)表示随机误差e(k)对应的设计阵。

层次模型构建的几个关键问题:层次模型结构中的层数、各层结构中的解释变量、各层结构中变量的概率分布，以及联结期望结果与一组解释变量之间的关联函数。模型一旦确定，下一步就是对各种参数的估计理论和方法。

2 模型统计推断发展理论

Lindley＆Smith(1972)在研究对线性模型的贝叶斯估计方法时，提出了一个针对复杂误差结构嵌套数据的研究框架模型;但该模型的应用需要对非平衡数据进行协方差成分的估计，仅能解决一些极简单的问题。Dempster，Laind＆Rubin(1977)提出的求参数极大似然估计的最大期望算法(Expectation-maximization algorithm，简称EM算法)，此算法从技术上突破了协方差成分估计的障碍。随后形成了解决方差协方差估计的3种不同思路:基于完全最大似然法(MLF)的迭代广义最小二乘估计(Goldstein，1986)和Fisher得分算法(Longford，1987);基于限制最大似然法(mason et al.，1983;Raudenbush＆Bryk，1986)的限制迭代广义最小二乘估计(Goldstein，1989)和基于贝叶斯的马尔科夫链蒙特卡罗迭代算法(MCMC)(Gelman et al，1995;Gilks et al，1996;Carlin ＆ Louis，1996;Raudenbush ＆ Bryk，2002)。

随后开发了大量统计程序和软件来拟合层次模型，如VARCL(Longford，1988)、BUGS(Spiegelhalter et al.，1994)、SAS 子程序 Proc Mixed(Little et al.，1996)、MIXOR(Hedeker ＆ Gibbons，1996)、MLWIN(Rasbash et al.，2000)和 HLM(Raudenbush et al.，2000)等。

我国学者在层次模型的理论方面取得一定的成果，如探讨了纵向数据混合效果方差分量估计(王松桂、吴密霞，2002);层次模型的统计诊断并提出了高水平单元的局部影响分析方法(石磊，2008);将灰色系统的建模思想融入层次模型构建了系列累加多层统计模型(刘殿国，2009)。系列专(译)著对层次模型的基本理论进行了阐述(王济川等，2010;郭志刚等，2007;温福星，2009;陈华珊等译，2011)。

基于完全最大似然法(MLF)的估计法基本原理:通过选择待估参数的估计值，使得观测到的这一实际数据的似然值达到最大。这一估计方法具有一系列大样本的优良特性:一致性、渐进有效性、抽样分布正态性以及待估参数的函数估计便捷性等。但基于完全最大似然法的方差协方差估计依赖于固定参数的点估计，为此，提出限制最大似然法(MLR)，对固定参数的不确定性进行调整，以适用于对于层次模型中高阶层单位数量较小且数据平衡的情况。而MLF和MLR在对固定参数进行区间估计和假设检验的统计推断时，都依赖于方差协方差参数的点估计的准确度。这使得MLF和MLR方法都存在局限性。而基于贝叶斯分析的估计方法，对参数的推断仅依赖于给定数据的后验分布，能够适用于高阶层单位数量较小且数据可能不平衡的情况。经研究证明，基于贝叶斯的方法能够有效地解决层次模型中的小样本、数据不平衡以及辅助参数不确定而影响焦点参数推断等问题。因为完全的贝叶斯方法可以确保对每个参数的推断都完全顾及所以其他参数的不确定性;不过该法也要求对所有参数设置先验分布，而先验分布的确定正是贝叶斯理论的关键问题。另外，后验分布的计算也是至关重要的问题。

3 基本模型的拓展

基本层次模型具有两个特征:假设各层兴趣参数的期望能够表为回归系数的线性函数和各层的随机效应为正态分布。通常线性假定与正态假定并不完全符合现实。为了使层次模型具有更为广泛地应用，得拓展基本层次模型。

首先，对模型的结果变量范围进行拓展形成的分层一般化线性模型。基本模型的结果变量主要指连续型变量，所以，拓展的第一步就是结果变量为离散型的。Stiratelli、Laird＆Ware(1984)，Wong＆Mason(1985)利用极大似然估计的一阶近似来解决这类问题。Goldstein(1995)提出二阶近似法;Hedeker＆Cibbons(1993)和Pinheiro＆Bates(1995)提出利用高斯-赫米特积分变换处理极大似然值的近似计算法;Raudenbush、Yang＆Yosef(2000)提出了更准确、更便利的基于高阶拉普拉斯变换的近似计算法。分层一般化线性模型主要包括二分类结果模型、计数数据模型、序次分类和多名义分类结果模型等。分层一般化线性模型与基本模型不同点在于其层-1模型的组成结构为3部分:抽样模型、连接函数和结构模型。比如，在二分类结果模型中，层-1抽样模型为二项抽样模型，记为

其中，Yij表示为mij次试验当中“成功”的数量;φij表示每一次试验中的成功概率。则E(Yij|φij)=mijφij，Var(Yij|φij)=mijφij(1-φij)。

层-1连接函数最便利的为logit连接函数，记为

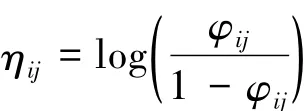
表示成功发生比的对数比。

层-1结构模型为线性结构模型，记为

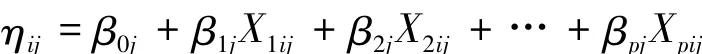
其次，针对缺失数据的潜在变量分层模型。基本模型主要针对完整数据进行的推断分析，而现实中往往存在缺失数据或不可观测的潜在变量。Little＆Rubin(1987)指出，若把观测数据看作残缺数据，则完整数据=残缺数据+缺失数据，潜在变量的分析就变成缺失数据问题。针对潜在变量，可以利用中间变量与潜在变量的关联性进行间接推断，而关联性由可观测的中间变量值和带有误差的数据在进行推断。Bock(1989)提出解决这一问题的两阶段推断问题:先解决潜在变量产生误差数据的机理;推断产生潜在变量的总体参数。

再次，针对嵌套结构更为复杂的交互分类层次模型。基本模型主要集中于严格的分层数据结构，而现实中往往存在较低层次的单位要面对两个或更多较高层次的单位进行交互分类。Raudenbush(1993)和Goldstein(1995)等都分别提出了相应的解决方法。

最后，基于贝叶斯推断的层次模型。层次模型中基于极大似然估计和经验贝叶斯的统计推断理论，面临高层单位数量很小且数据不平衡时，稳健性不太理想，基于设置所有参数先验分布的完全贝叶斯方法具有明显的优势(Gelfand et al，1990;Seltzer，1993，1996)。Gelman et al(1995)证明了利用贝叶斯方法解释但依赖经典方法评估由先验分布所计算的估计和检验的合理性是可能的;Carlin＆Louis(1996)证明了在层次模型中，贝叶斯估计量在许多样本中具有良好性质。Gilks et al(1996)和Browner(2004)等提出了基于贝叶斯理论的马尔科夫链蒙特卡罗迭代算法(MCMC)，Spiegelhalter et al(1994)开发了相应软件BUGS等。

4 层次模型的应用及展望

层次模型已广泛应用于教育学、人口学、组织学、社会学、心理学、经济学和公共卫生等各个领域。环境科学也引进了层次模型和贝叶斯方法(Morris，1983;Ver Hoef，1990;Clark，2003，2006;Song S.Qian，2010)，如CO2浓度的增加对火炬松冠层下幼苗生长速率的影响研究(Mohan et al，2006);并进行了R软件开发(Clark，2007)。我国对层次模型也已广泛应用于教育学、社会学、心理学、经济学和公共卫生等各个领域(张雷等，2002;杨珉等，2007;王济川等，2008;石磊等，2013)。

综上所述，在近三十多年的发展，层次模型无论在理论方面，还是应用方面，都取得了很多成果，成为了统计学科的一个热门前沿领域。层次模型的未来发展，若与当前统计学科的另一热点结构方程理论有机结合，将掀起统计学科的下一个发展热潮。另外，若将灰色理论和模糊统计融入，将开辟更广泛的统计领域。

［1］GOLDSTEIN H.Multilevel Statistical Models［M］.3nd.New York:Halsted Press，2003

［2］RAUDENBUSH S，BRYK A.Hierarchical linear models:applications and data analysis methods［M］.2nd.Thousand Oaks:Sage Publications，2002

［3］王济川，谢海义，姜宝法.多层统计模型:方法与应用［M］.北京:高等教育出版社，2010

［4］张雷，雷雳，郭伯良.多层次线性模型应用［M］.北京:教育科学出版社，2002

［5］石磊，向其凤，陈飞.多水平模型及其在经济领域中的应用［M］.北京:科学出版社，2013

［6］CLARK J.面向生态学数据的贝叶斯统计［M］.沈泽昊，译.北京:科学出版社，2013