复摩擦摆隔震性能的振动台试验研究

翁大根，周 源，赵 阳，任晓崧，丁孙玮

（1.同济大学土木工程学院，上海 200092；2.上海材料研究所，上海 200437）

复摩擦摆隔震性能的振动台试验研究

翁大根1，周 源1，赵 阳1，任晓崧1，丁孙玮2

（1.同济大学土木工程学院，上海 200092；2.上海材料研究所，上海 200437）

通过模型振动台试验研究采用复摩擦隔震支座（MFPB）的楼面隔震性能。试验结果表明，隔震层上部荷载变化对MFPB隔震效果没有影响；MFPB与黏滞阻尼器的协同工作能够控制隔震楼面的位移；竖向地震动对MFPB的水平隔震效果无明显影响；用SAP2000中的摩擦连接单元模拟MFPB隔震效果的精度是满足工程需求的。

复摩擦摆支座；振动台试验；黏滞阻尼器；竖向地震输入

工程结构隔震技术最重要的环节之一就是设计出合理可靠的隔震装置。现今工程应用上较为常见的隔震支座按照其隔震原理与特性主要可分成：类弹簧式隔震支座、滑动式隔震支座以及混合式隔震支座三大类［1］。纯滑动式隔震支座因缺乏足够的回复力，导致隔震结构在震后会留下较大的残余位移；混合式隔震支座综合了类弹簧式隔震支座与滑动式隔震支座的特性，既可通过低摩擦系数的滑动界面隔离地震能量的输入，也可改变结构的基本周期。目前常见的混合式隔震支座主要是摩擦单摆隔震支座（FPB）。该种隔震支座于1985年由美国的Zayas等［2］提出，其隔震消能的主要原理是利用滑动面的设计来延长结构的振动周期，以大幅度减小因地震作用而引起的动力放大效应。FPB具有良好的稳定性、复位能力和抗平扭能力，目前已经在工程中开始推广应用。

蔡崇兴等于2004年改进了摩擦摆系统，研发出了复摩擦摆系统（MFPS），MFPB具有上下两个支座板和一个铰接滑块，依靠摆动时上下滑块表面的低摩擦材料的摩擦来消耗能量，由于滑动面为球面，可以依靠重力自动复位，减小支座震后的残余位移，与FPB不同的是，MFPB具有上下两个滑动摩擦球面使其位移容量为相同参数的FPB的两倍，其滑动状态的示意图如图1所示。蔡崇兴等对MFPB隔震缩尺和足尺钢结构进行了振动台试验，分别输入了远、近断层地震记录，并考察了多维地震作用下的隔震效果。结果表明，MFPB隔震体系在长短周期的多维地震激励下均能有效的隔离地震，与固定基础结构相比，各楼层的绝对加速度响应显著减小，而且在强震下结构构件的应力反应限制在一定范围，MFPB的残余位移可以忽略不计［3－4］。Constantinou和Fenz进一步研究了上下滑动面曲率半径和摩擦系数不等情况的MFPB，提出了基于平衡考虑的恢复力模型，并进行了试验验证，指出MFPB设计和分析中需要注意的问题，并且介绍了MFPB的六层钢框架结构模型的试验以及隔震系统的安装［5－7］。邓雪松等［8］利用ABAQUS软件对MFPB进行了实体单元建模，数值模拟了低周反复荷载作用下MFPB的滞回特性和回复特性。

本文在国内外已有工作基础上，通过振动台模型试验，重点研究隔震层上部质量变化对MFPB隔震效果的影响、MFPB与黏滞阻尼器协同工作的减震效果以及竖向地震动对MFPB隔震效果的影响。期望通过这种试验，研究MFPB的隔震性能并应用于结构隔震工程。

图1 复摩擦摆支座示意图Fig.1 Schematic diagram of MFPB

1 MFPB楼面隔震振动台试验概述

1.1 MFPB楼面隔震模型

试验模型使用了刚性构架和质量块MFPB隔震体系上部结构，刚性框架为4.4m×4.4m钢构架，模型配重分别为2.8 t和7.6 t。隔震层采用4个MFPB，部分工况采用4个MFPB＋2个黏滞阻尼器。试验所用的MFPB的上下滑动面曲率半径相等、摩擦系数相等。试验的照片如图2、3所示。试验所用的MFPB和黏滞阻尼器的相关参数如表1、2所示。

图2 MFPB楼面隔震振动台试验模型（无配重）Fig.2 Model of floor isolation with MFPB on shaking table（No additionalmass）

图3 MFPB楼面隔震振动台试验模型（无配重）Fig.3 Model of floor isolation with MFPB on shaking table（4.8 tonsmass additional）

表1 试验MFPB的参数Tab.1 Parameters of MFPB in test

表2 试验用黏滞阻尼器的参数Tab.2 Parameters of viscous dam per

1.2 MFPB支座楼面隔震模型测点布置

在MFPB楼面隔震振动台试验中，测量仪器的选用见表3，位置和布置图分别见表4和图4、5。因本试验的楼面隔震结构在水平向具有对称性，水平向仅研究在X向地震输入下的楼面响应。隔震楼面X向的响应数据测点均有两个，在处理时取两个测点中峰值较大者。

表3 测量仪器数目Tab.3 Num ber ofmeasuring instrum ents

表4 试验数据测点Tab.4 Measuring points for test data

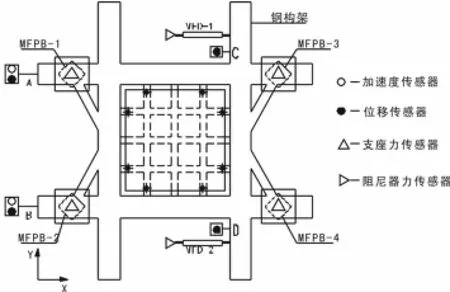
图4 试验传感器布置图Fig.4 Sketch of arrangement for sensors in test

1.3 本试验输入地震波选取

考虑到试验振动台参数限制，试验地震输入的特征周期取0.3 s。因此，取规范［9］中阻尼比ζ＝0.02，Tg＝0.30 s的归一化反应谱作为试验目标反应谱，具体公式如式（1）所示。参照该目标反应谱生成一条人工地震时程3，选择两条实际地震记录时程1和2，以此三条地震时程作为输入研究MFPB隔震楼面在地震下的响应。三条时程的归一化加速度谱与目标反应谱的对比见图6。三条时程的归一化加速度时程曲线如图7、8、9。在时程的峰值段，MFPB支座的变位比较充分，能够充分发挥隔震作用，因此在处理实验结果时，截取各个时程峰值段的响应作为研究对象。如图7、8、9所示，时程1加速度曲线的峰值段取5～15 s区间，时程2加速度曲线的峰值段取2～16 s区间，时程3加速度曲线的峰值段取3～12s区间。

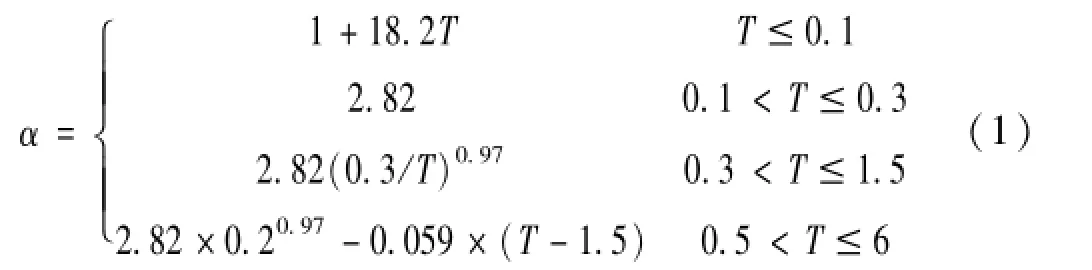
图5 部分传感器布置照片Fig.5 Photos of arrangement for sensors in test

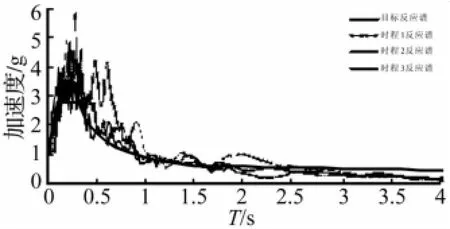
图6 各条时程归一化加速度谱与目标反应谱的比较Fig.6 Comparison between target spectrum and normalized response spectrum of each time history

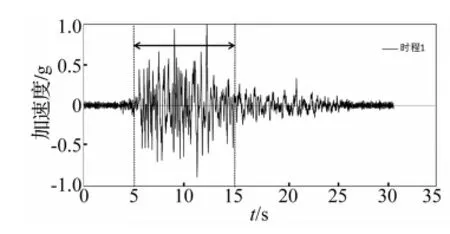
图7 时程1归一化加速度时程曲线Fig.7 Normalized acceleration curve of time history 1

图8 时程2归一化加速度时程曲线Fig.8 Normalized acceleration curve of time history 2

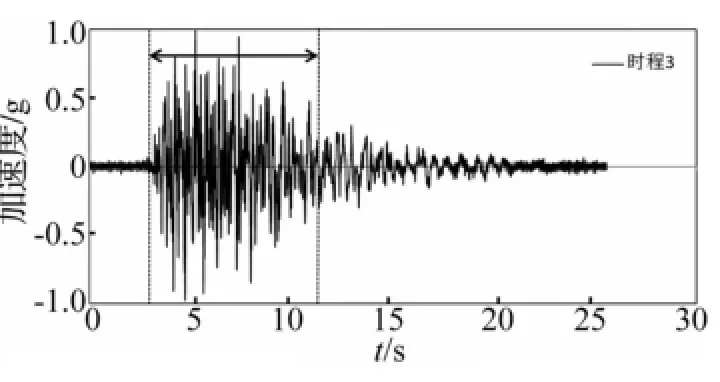
图9 时程3归一化加速度时程曲线Fig.9 Normalized acceleration curve of time history 3

1.4 试验加载工况

本试验的加载工况如表5所示，共有16个加载工况。根据研究目的不同分为三个对比组，如表6所示。

对比组1：研究隔震体系上部质量改变对隔震楼面地震响应的影响。

对比组2：研究MFPB与黏滞阻尼器协同工作的隔震方式的隔震效果。

对比组3：研究竖向地震输入对隔震楼面水平地震响应的影响。

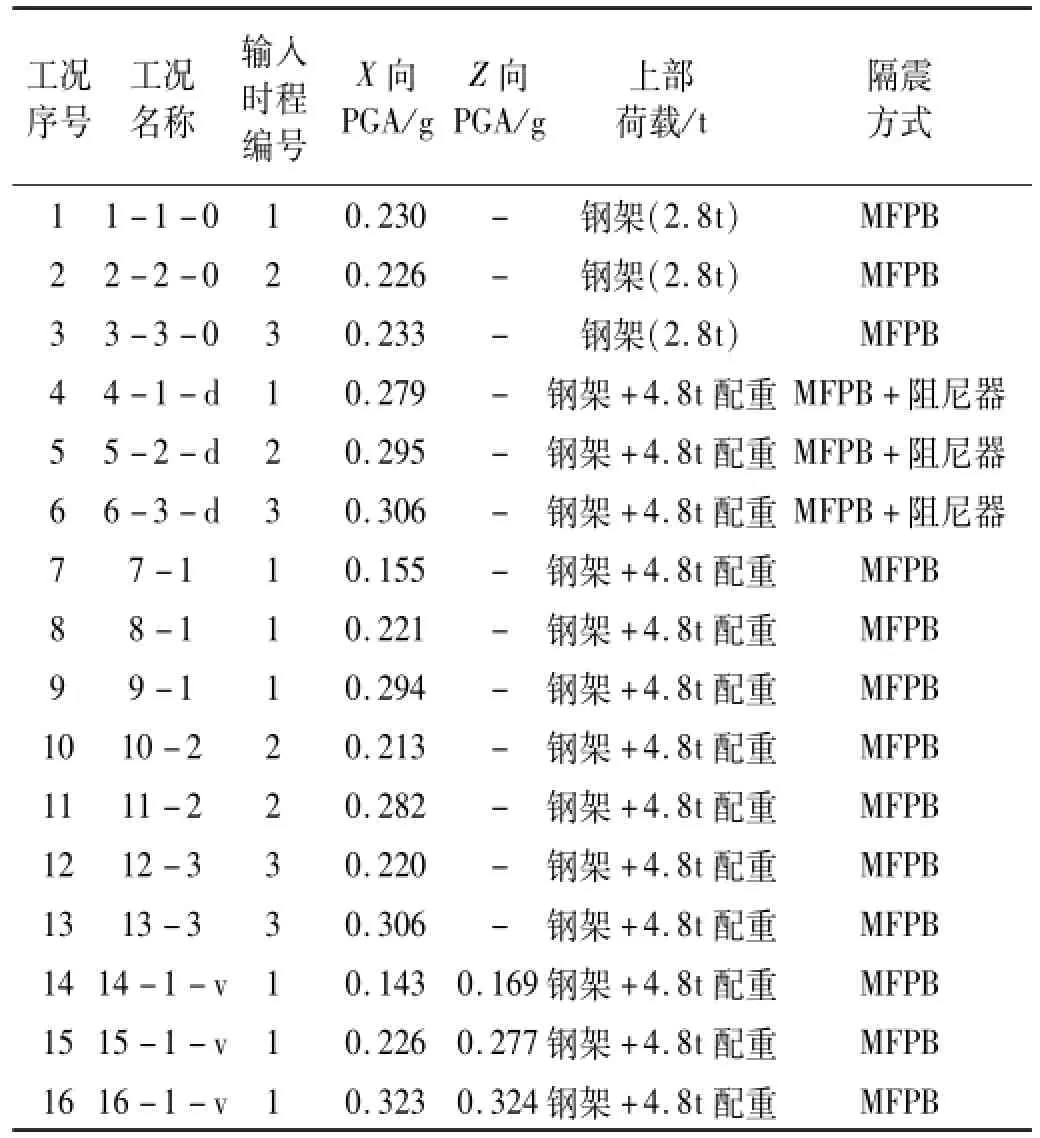
表5 楼面隔震试验加载工况表Tab.5 Loading cases for floor isolation test

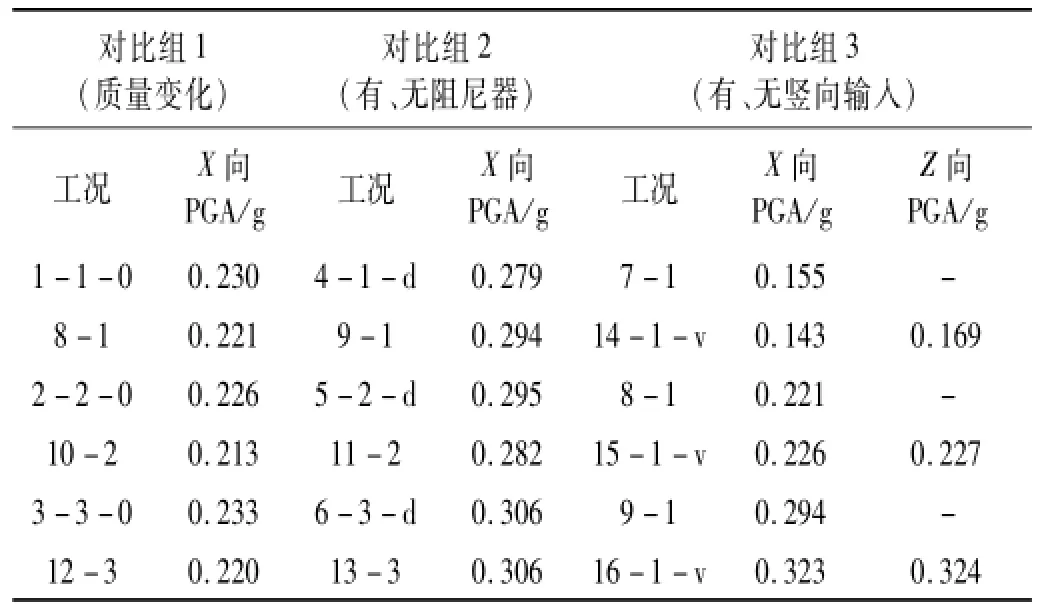
表6 各对比组中相应工况的比较Tab.6 Com parison of corresponding cases in each group

2 振动台试验结果分析

2.1 隔震体系上部质量变化对水平隔震效果的影响

试验的对比组1中工况1－1－0、2－2－0、3－3－0与工况8－1、10－2、12－3的区别在于隔震楼面上部质量的不同，前者上部质量为钢构架自重2.8 t，后者为钢构架自重加混凝土配重7.6 t。对比在相同地震输入下（两组输入加速度峰值基本接近），两组工况的楼面绝对加速度和层间位移响应，研究MFPB隔震体系的上部质量变化对其水平向隔震效果的影响，其振动台试验结果如表7（amax、dmax分别表示绝对加速度峰值和层间位移峰值）和图10～11，限于篇幅，图中仅列出了工况1－1－0和工况8－1的楼面响应时程对比。

从表7可以看出，隔震体系上部质量从2.8 t上升至7.6 t后，隔震楼面的个别时间点绝对加速度响应幅值存在变化，减小了约30%左右，但是整个时程变化不大；其层间位移响应幅值变化微小。图10显示上部荷载变化前后楼面的加速度响应曲线较吻合；而图11显示上部荷载变化前后的层间位移响应曲线在峰值段较为接近，在末尾段，曲线的差别较大，但这种差别并不影响对隔震效果的判断。因此，MFPB隔震体系上部质量的改变，对隔震体系的绝对加速度和层间位移响应的影响微小。

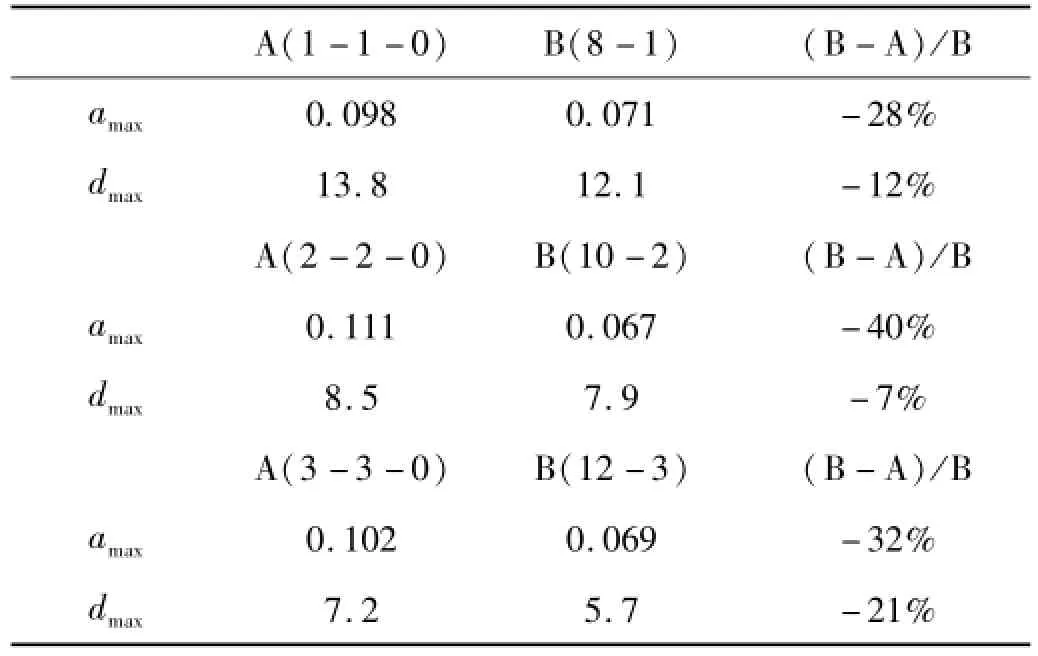
表7对比组1相应工况响应的对比（g、mm）Tab.7 Com parison of response between corresponding cases in group 1

2.2 MFPB＋黏滞阻尼器的组合方式隔震效果

试验的对比组2中工况4－1－d、5－2－d、6－3－d采用的MFPB＋黏滞阻尼器的隔震方式，工况9－1、11－2、13－3是仅有MFPB的隔震方式，这两组工况时程输入的加速度峰值接近，其振动台试验结果如表8和图12～13，限于篇幅，图中仅列出了工况4－1－d和工况9－1的楼面响应时程对比。从表8可以看出，增加了黏滞阻尼器之后，楼面绝对加速度响应增加了40%以上，而层间位移减少了20%左右。可见通过增加隔震结构的阻尼，可控制层间位移，但需要牺牲部分隔震效果。在实际使用中，需要设计人员在位移的控制和隔震效果之间找到最佳的平衡点。

工况9－1与工况4－1－d的层间位移对比（图13），在工况9－1的地震作用下，楼面发生脉冲型的相对变位，在工况4－1－d中该脉冲变位被显著减弱。这是因为增加了黏滞阻尼器之后，其阻尼力能够随着输入的加速度增大提高而持续增长，而MFPB的阻尼力的增长会趋向平稳。因此，当遇到脉冲型地震波时，控制隔震结构的位移变得尤为重要，在这种情况下应该采用黏滞阻尼器与MFPB协同工作的隔震方法以达到有效的控制隔震结构位移的目的，减少隔震结构所需的隔震缝。

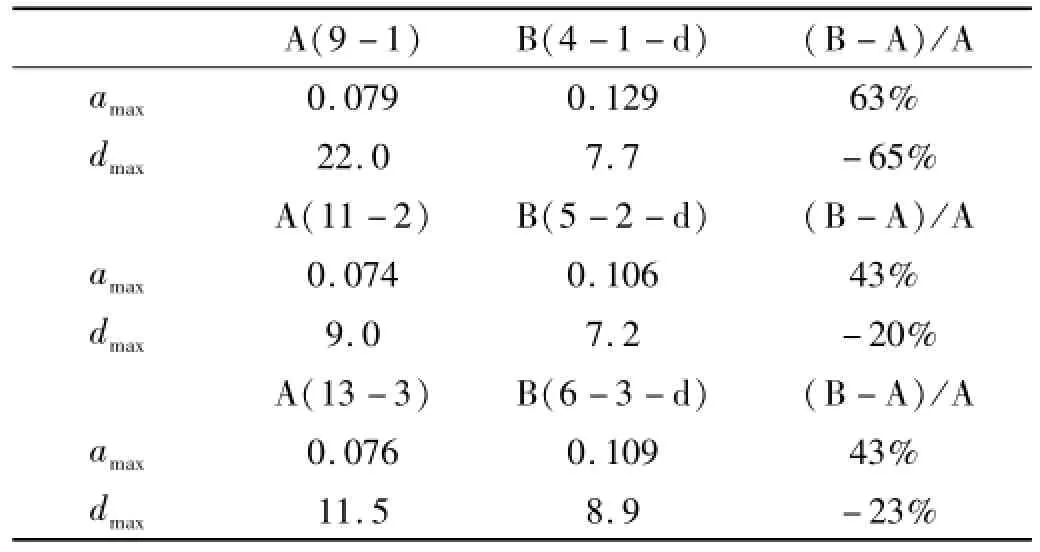
表8 对比组2相应工况响应的对比（g、mm）Tab.8 Comparison of response between correspond ing cases in group 2

图10 工况1－1－0、8－1楼面绝对加速度响应对比Fig.10 Comparison of floor absolute acceleration responses between case 1－1－0 and 8－1

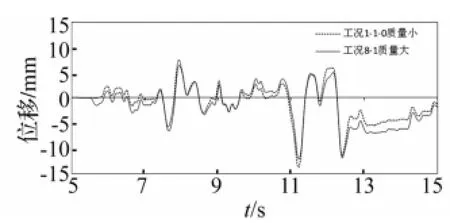
图11 况1－1－0、8－1层间位移响应对比Fig.11 Comparison of story displacement responses between case 1－1－0 and 8－1

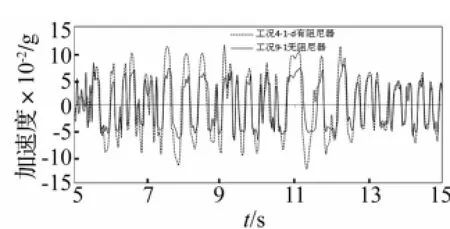
图12 工况4－1－d、9－1楼面绝对加速度响应对比Fig.12 Comparison of floor absolute acceleration responses between case4－1－d and 9－1

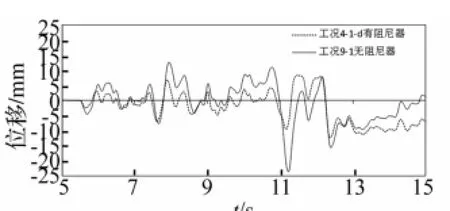
图13 工况4－1－d、9－1层间位移响应对比Fig.13 Comparison of story displacement responses between case 4－1－d and 9－1

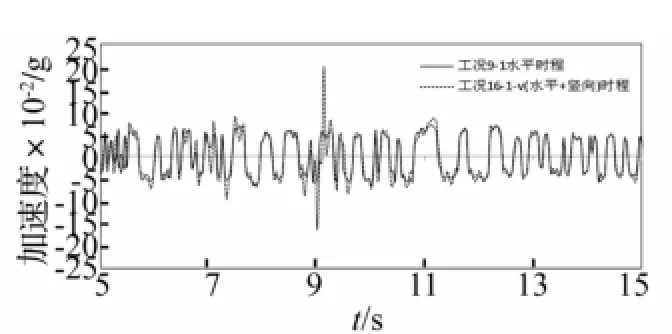
图14 工况9－1、16－1－v楼面绝对加速度响应对比Fig.14 Comparison of floor absolute acceleration responses between case 9－1 and 16－1－v

图15 工况9－1、16－1－v层间位移响应对比Fig.15 Comparison of story displacement responses between case 9－1 and 16－1－v

2.3 竖向地震动对MFPB水平隔震效果的影响

目前常用的MFPB分析模型适用于微幅振动，并假定滑块对滑道正压力在滑块的运动中是不变的，无法考虑竖向地震动的影响［10］。试验的对比组3的目的是研究竖向地震动对MFPB水平隔震效果的影响。

试验工况7－1、8－1、9－1为仅有水平X向地震输入的工况，工况14－1－v、15－1－v、16－1－v为（X向＋Z向）地震输入的工况，两组的水平向地震时程输入的加速度峰值接近，可以研究MFPB隔震楼面在存在竖向地震激励的情况下的隔震效果，试验结果如图14～15所示，限于篇幅，仅列出了工况9－1和工况16－1－v的楼面响应时程对比。图14表明加入竖向地震激励之后，楼面绝对加速度响应仅在个别峰值点存在差异，取峰值差异最大的工况9－1和16－1－v的楼面绝对加速度响应时程并对比二者的反应谱，如图16所示二者的加速度反应谱基本吻合，因此竖向地震输入对楼面的绝对加速度响应无明显影响；而图15则表明增加竖向地震激励前后的层间位移响应无明显变化。因此，竖向地震动对MFPB的水平隔震效果影响微小。

2.4 试验中MFPB滞回曲线

图17～18列出了试验当中部分工况的MFPB的水平力－位移滞回曲线。

3 振动台试验与有限元分析结果对比

MFPB楼面隔震振动台试验的目的是为了全面地研究MFPB的隔震效果，通过有限元方法模拟MFPB隔震楼面结构并将有限元模拟的结果与试验结果对比，验证计算分析的准确性，为实际应用提供依据。

目前的有限元分析软件没有通用的MFPB单元，部分软件如SAP2000有可用来模拟FPB的摩擦连接单元（Friction Isolator）。根据MFPB与FPB理论模型的比较，可知在上下曲率半径相等、摩擦系数相等的情况下，MFPB可近似用FPB进行分析，此FPB的曲率半径为MFPB的上下滑道曲率半径之和，摩擦系数与MPFB上下滑道摩擦系数相等［11］。

工况9－1、11－2、13－3的地震输入的加速度峰值较大，MFPB的位移较大，滞回曲线较为饱满，具有一定的代表性，可取此三个工况的试验数据作为有限元模拟的参照。根据工况9－1的试验数据获取MFPB的力学参数，建立SAP2000的有限元模型，分别输入工况9－1、11－2、13－3中的地震波进行时程分析，将得到的SAP2000分析结果与工况9－1、11－2、13－3的振动台试验结果对比，验证SAP2000中MFPB参数设置的合理性。

图16 工况9－1、16－1－v楼面绝对加速度反应谱对比Fig.16 Comparison of floor absolute acceleration response spectrums between case 9－1 and 16－1－v

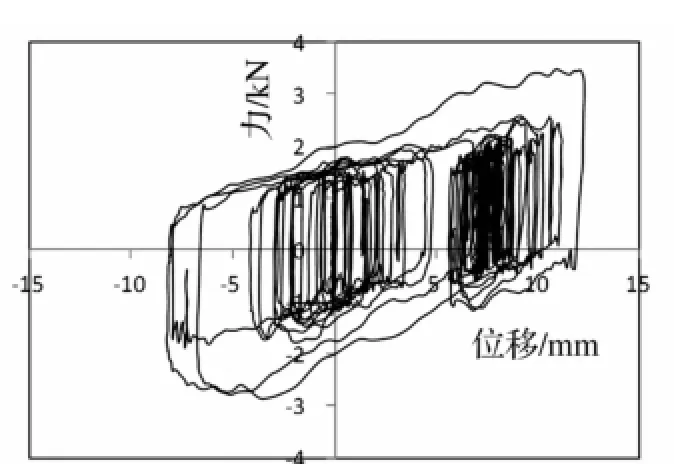
图17 工况4－1－d MFPB水平力－位移滞回曲线Fig.17 Horizontal force-displacement hysteresis loop of MFPB under case 4－1－d

图18 工况9－1MFPB水平力－位移滞回曲线Fig.18 Horizontal force-displacement hysteresis loop of MFPB under case 9－1

MFPB的等效线性化分析模型如图19所示，在支座设计中，几个关键参数的物理含义为：Ki为初始刚度，其表达式如式（2），Dy为材料的屈服位移，据有关试验报告，铁氟龙材料的屈服位移约在0.2～0.5mm的范围，本模型取为0.45 mm；KMFPS为MFPB的摆动刚度；Keff为支座的等效线性刚度，其表达式如式（3），式中Dd为支座的设计位移。

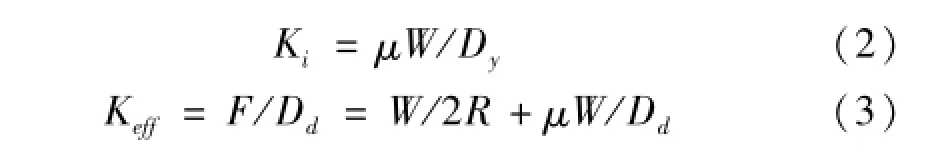
图19 MFPB等效线性化滞回模型Fig.19 Equivalent linear hystereticmodel ofMFPB

连接单元的参数设置中：慢、快摩擦系数均按试验的实际情况取值，MFPB曲率半径取上下滑动面曲率半径之和；比例指数取为15～30m－1［13］。则在SAP2000中模拟试验工况9－1的MFPB参数设置如表9所示。

表9 计算中MFPB参数设置Tab.9 Parameters setting of MFPB in calculation

对比结果如表10所示，SAP2000与试验的结果误差极小；图20和21分别是工况9－1试验和SAP2000计算的楼面绝对加速度响应、层间位移响应的对比，可以看出试验与SAP2000模拟的结果较吻合；图22表示工况9－1试验与SAP2000模拟的MFPB滞回曲线，二者曲线的吻合程度较高。因此用摩擦连接单元来模拟MFPB是可行的。

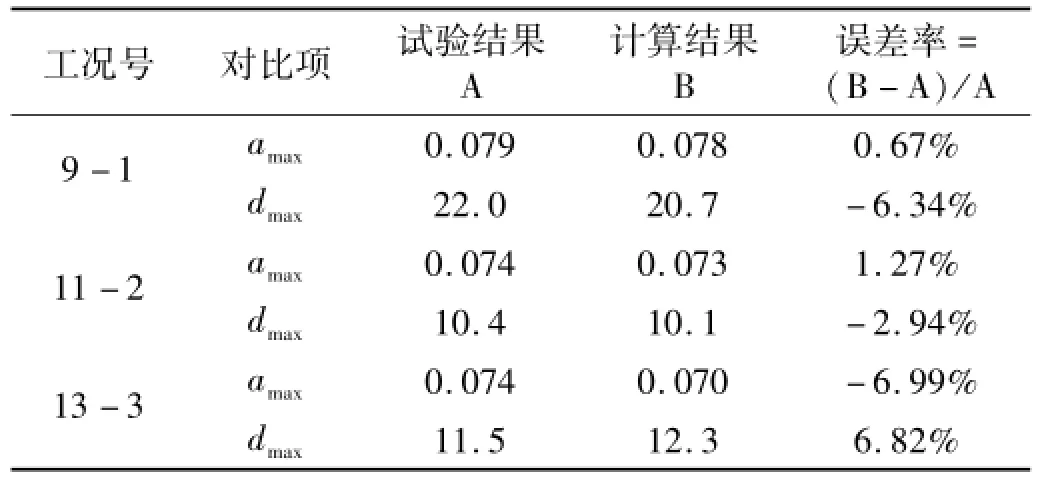
表10 试验与SAP2000计算响应对比（g、mm）Tab.10 Com parison of response between SAP2000 and test

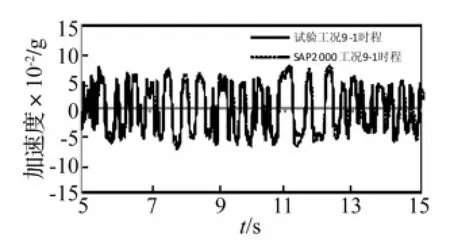
图20 工况9－1试验与计算楼面绝对加速度响应对比Fig.20 Comparison of floor absolute acceleration responses between test and calculation under case9－1

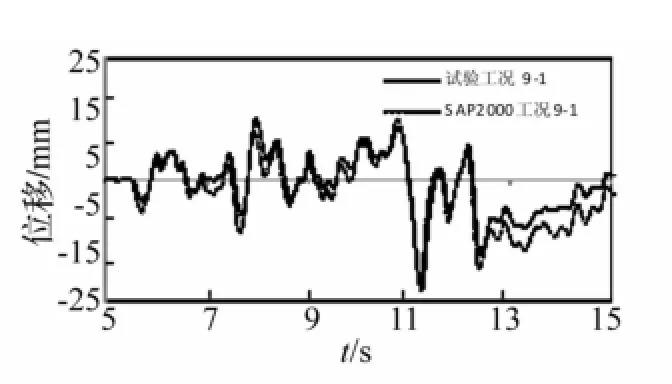
图21 工况9－1试验与计算层间位移响应对比Fig.21 Comparison of story displacement responses between test and calculation under case 9－1

图22 工况9－1试验与计算MFPB滞回曲线对比Fig.22 Comparison of hysteresis loop of MFPB between test and calculation under case 9－1

图23 工况3－3－0试验与计算楼面绝对加速度响应对比Fig.23 Comparison of floor absolute acceleration responses between test and calculation under case3－3－0

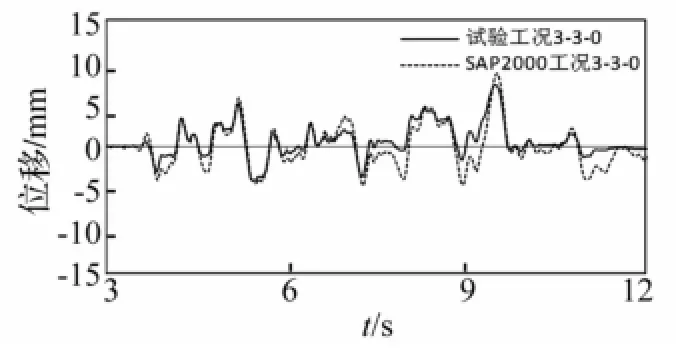
图24 工况3－3－0试验与计算层间位移响应对比Fig.24 Comparison of story displacement responses between test and calculation under case3－3－0

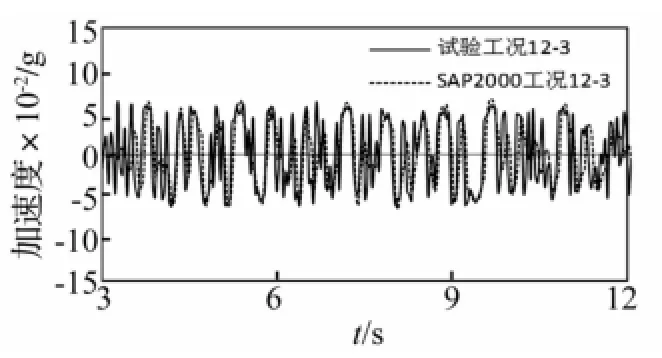
图25 工况12－3试验与计算楼面绝对加速度响应对比Fig.25 Comparison of floor absolute acceleration responses between test and calculation under case 12－3

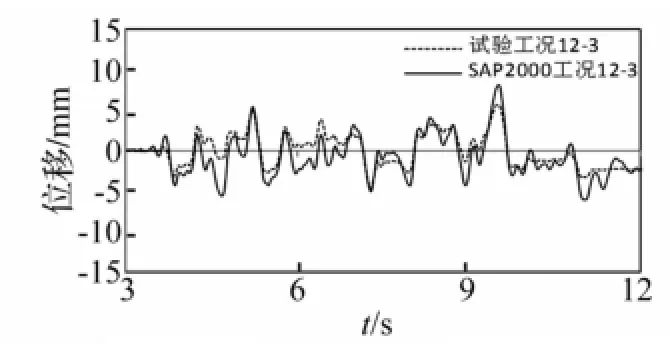
图26 工况12－3试验与计算层间位移对比Fig.26 Comparison of story displacement responses between test and calculation under case 12－3

图27 工况6－3－d试验与计算楼面绝对加速度响应对比Fig.27 Comparison of floor absolute acceleration responses between test and calculation under case 6－3－d

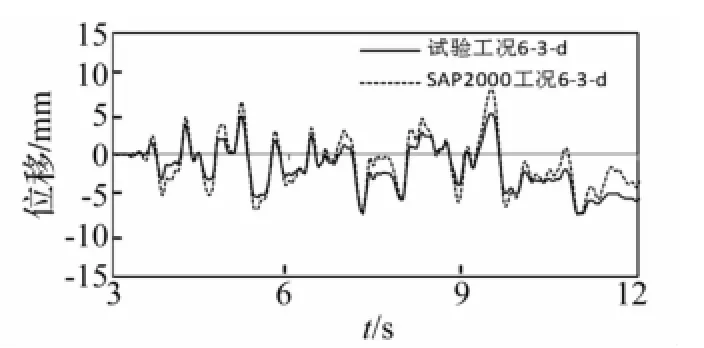
图28 工况6－3－d试验与计算层间位移对比Fig.28 Comparison of story displacement responses between test and calculation under case 6－3－d

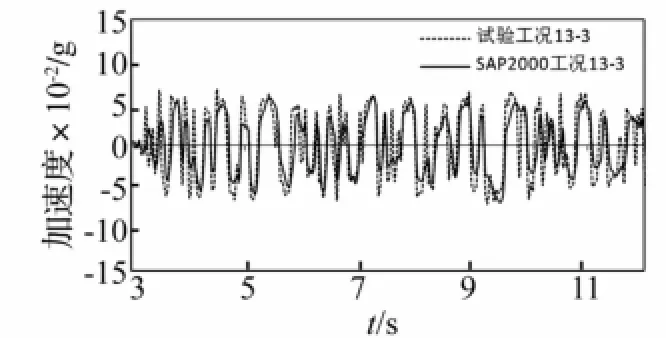
图29 工况13－3试验与计算楼面绝对加速度对比Fig.29 Comparison of floor absolute acceleration responses between test and calculation under case 13－3

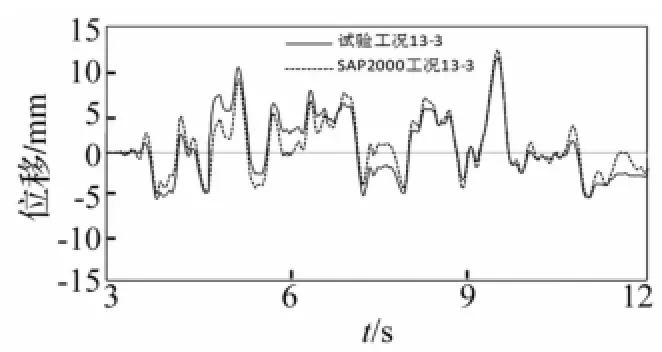
图30 工况13－3试验与计算层间位移响应对比Fig.30 Comparison of story displacement responses between test and calculation under case 13－3

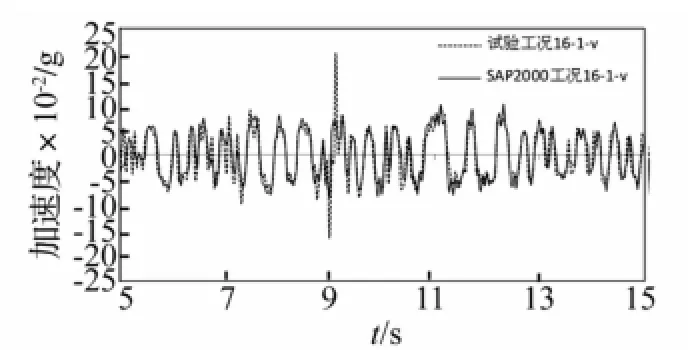
图31 工况16－1－v试验与计算楼面绝对加速度响应对比Fig.31 Comparison of floor absolute acceleration responses between test and calculation under case 16－1－v

根据上述的分析结果，在SAP2000里分别建立试验当中三个对比组的模型，输入各个对比组中工况的时程数据进行分析，整理SAP2000的计算结果，并与试验的结果对比，如图23～32所示。

对比组1中的工况3－3－0、12－3的试验与SAP2000计算结果的对比如图23～26所示，图23、24显示工况3－3－0的楼面绝对加速度响应、层间位移响应的试验结果与SAP2000计算结果较为吻合，图25、26显示工况12－3亦然，表明MFPB楼面隔震结构上部质量变化对水平隔震效果没有影响。

对比组2中工况6－3－d、13－3的试验与SAP2000计算结果的对比如图27～30所示，图27、28显示工况6－3－d的楼面绝对加速度响应、层间位移响应的试验结果与SAP2000计算结果较为吻合，图29、30显示工况13－3亦然，表明了黏滞阻尼器与MFPB组合的隔震方式能够控制隔震体系的位移。

对比组3中工况16－1－v的试验与SAP2000计算结果的对比如图31、32所示，工况9－1的类似对比已在前图20、21中列出，图31和32显示工况16－1－v的楼面绝对加速度响应、层间位移响应的试验结果与计算结果较为吻合，前图20、21显示工况9－1亦然，表明竖向地震动对MFPB隔震楼面的水平绝对加速度响应和层间位移响应的影响较小。

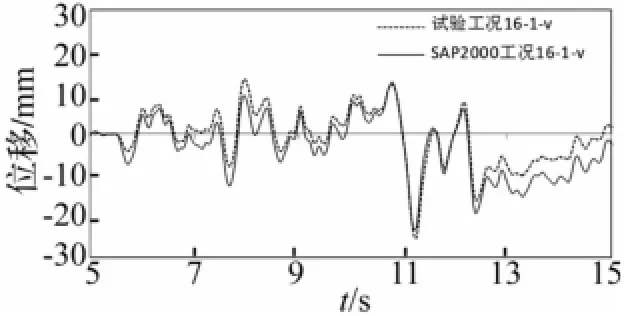
图32 工况16－1－v试验与计算层间位移响应对比Fig.32 Comparison of story displacement responses between test and calculation under case 16－1－v

4 结 论

本文通过对MFPB楼面隔震振动台试验和SAP2000有限元模拟结果的分析得出以下结论：

（1）MFPB隔震体系上部质量的改变，对隔震体系绝对加速度响应和层间位移响应的影响微小；

（2）MFPB与黏滞阻尼器协同工作的组合隔震方式能有效控制隔震体系的位移，尤其是对于脉冲型地震波作用下的结构变位。但需要设计者在层间位移的控制和隔震效果之间找到一个最佳的平衡点；

（3）竖向地震动对MFPB楼面隔震的水平隔震效果无明显影响；

（4）通过数值分析与试验结果的对比，表明了用程序自带的摩擦连接单元来模拟MFPB的方法是可行的，便于MPFB在隔震工程应用中的推广；

（5）振动台面输入的加速度较小，导致MPFB的位移行程没有充分发挥，这是本次试验考虑不足之处。

［1］江子政.复摆隔震器于防震工程之应用［D］.台中：逢甲大学，2004.

［2］Zayas V A，Low SA，Mahin S.The FPSearthquake resisting system［R］.Technical Report UCB／EERC－87／01，University of California at Berkeley，1987.

［3］Tsai C S，Chiang T C，Chen B J.Experimental study for multiple Friction Pendulum system［C］.Proceedings，13th World Conference on Earthquake Engineering，2004.

［4］Tsai C S，Chen W S，Chiang T C，et al.Component and shaking table tests for full-scale multiple friction pendulum system［J］.Earthquake engineering＆structural dynamics，2006，35（13）：1653－1675.

［5］Constantinou MC.Friction Pendulum double concave bearing［J］.NEESReport，2004.

［6］Fenz D M，Constantinou MC.Behavior of the double concave Friction Pendulum bearing［J］.Earthquake engineering＆structural dynamics，2006，35（11）：1403－1424.

［7］Constantinou MC，Carpenter J A.Six-story test isolated structure［R］.SUNY，Buffalo，NY，Nov.，2004.

［8］邓雪松，龚 健，周 云.双凹摩擦摆隔震支座理论分析与数值模拟研究［J］.广州大学学报：自然科学版，2010（004）：71－77.

DENG Xue-song，GONG Jian，ZHOU Yun.Study on the theoretical analysis and numerical simulation of double concave friction pendulum isolation bearing［J］.Journal of Guangzhou University：Natural Science Edition，2010（004）：71－77.

［9］中华人民共和国建设部.GB 50011－2010建筑抗震设计规范［S］.北京：中国建筑工业出版社，2011.

［10］巫 炜.摩擦摆隔震结构分析［D］.北京：北京交通大学，2007.

［11］赵 阳，翁大根，任晓崧，等.复摩擦摆支座应用于楼面隔震研究［J］.结构工程师，2012，28（1）：73－81.

ZHAO Yang，WENG Da-gen，REN Xiao-xong，et al.Study on floor isolation with multiple pendulum system［J］.Structural Engineers，2012，28（1）：73－81.

［12］Constantinou M，Mokha A，Reinhorn A.Teflon bearings in base isolation II：Modeling［J］.Journal of Structural Engineering，1990，116（2）：455－474.

［13］李大望，李桂青，周锡元.FPS隔震结构的水平和竖向振动响应分析［J］.建筑结构，2000（7）：61－64.

LIDa-wang，LIGui-qing，ZHOU Xue-yuan.Analysis for the horizontal and vertical vibration responses of base-isolated building with FPS bearings［J］.Building Structures，2000（7）：61－64.

Isolation efficiency check for multip le friction pendulum bearings using shaking table tests

WENGDa-gen1，ZHOU Yuan1，ZHAO Yang1，REN Xiao-song1，DING Sun-wei2
（1.College of Civil Engineering，Tongji University，Shanghai200092，China；2.Shanghai Research Institute of Materials，Shanghai200437，China）

The isolation efficiency ofmultiple friction pendulum bearings（MFPB）was checked with shaking table tests.The results showed that changes of load on the isolation layer have no influence on the isolation efficiency ofMFPB；combining MFPB with viscous dampers can control displacements of an isolated structure；the vertical seismic inputhas no significant impact on the horizontal isolation effect of MFPB；the simulation accuracy for isolation effect of MFPB with friction-connection elements in SAP2000 can meet the requirementof engineering applications.

multiple friction pendulum bearing；shaking table test；viscous damper；vertical seismic input

TU352.12

A

国家自然科学基金项目（51178355）；上海市科学技术委员会基金（10DZ2252000）

2013－07－24 修改稿收到日期：2013－09－24

翁大根男，博士，研究员，1952年10月生