基于分形插值函数生成的分形插值曲面的中心变差

孙秀清

（江苏联合职业技术学院镇江分院基础部，江苏镇江 212016）

基于分形插值函数生成的分形插值曲面的中心变差

孙秀清

（江苏联合职业技术学院镇江分院基础部，江苏镇江 212016）

介绍矩形域上一类分形插值曲面的构造方法，讨论这类分形插值曲面的中心变差的性质。

仿射分形插值函数；分形插值曲面；中心变差

Barnsley［1-2］在20世纪80年代首先提出了分形插值的概念，通过构造一类特殊的迭代函数系，可以生成处处连续处处不可导的插值函数，它被称为分形插值函数。分形插值为数据拟合提供了一种新的途径，在拟合非光滑曲线方面具有独特的优势。基于Barnsley提出的分形插值方法，许多学者对分形插值曲面（二元分形插值函数）构造方法展开了广泛的讨论［3-7］，并对分形插值曲面的性质，特别是曲面的分形维数，进行了研究。分析这些曲面的构造方法发现，为了保证分形插值曲面的连续性，他们都加上了插值节点边界共线或纵向尺度因子相等等条件限制，显然，这些条件与实际情况不相符合，从而制约了分形插值曲面的实际应用。Bouboulis和Dalla［8］提出了基于仿射分形插值函数的分形插值曲面的构造方法，解除了插值节点边界共线和纵向尺度因子相等的限制，使得插值方法更加灵活，适应范围更加广泛。笔者在此基础上，讨论这类分形插值曲面的性质，研究这类分形插值曲面的变差，为这类分形插值曲面的粗糙度讨论和分形维数的计算提供参考。

1 基于分形插值函数生成的分形插值曲面的构造

给定闭区间I=［a，b］，令

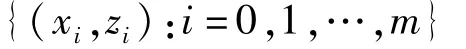
是I×R上的插值结点集，其中m≥2且为整数。对于给定实数组，其中

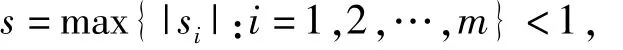
称为纵向尺度因子。对于i∈｛1，2，…，m｝，定义仿射映射

其中

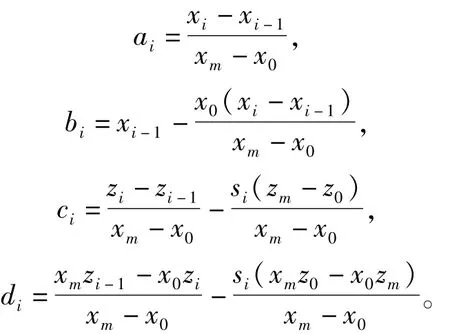
则构成一个对应于插值节点是

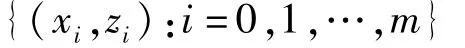
的迭代函数系

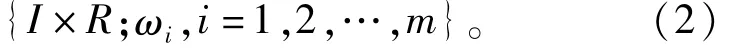
根据参考文献［1-2］，迭代函数系（2）有唯一不变集

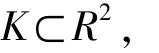
它是I上一连续函数f（x）的图象，即

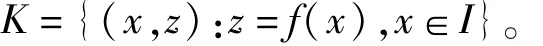
并且该函数过插值节点

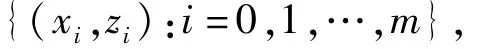
即如果

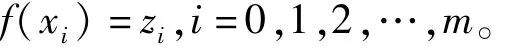
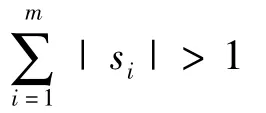
且插值结点不在一条直线上，那么K的计盒维数dimB（K）就是满足方程

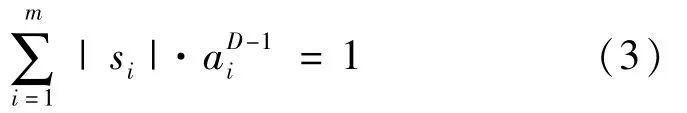
的唯一解D。否则，

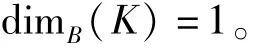
由于K的计盒维数常大于1，因此f（x）称为仿射分形插值函数。f（x）是迭代函数系

生成的仿射分形插值函数的一个充要条件是f（x）满足方程

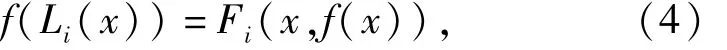
x∈I，i=1，2，…，m。

设

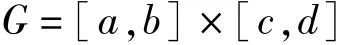
是R2中的矩形域，

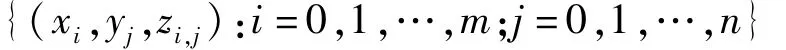
是R3中的一点集，其中

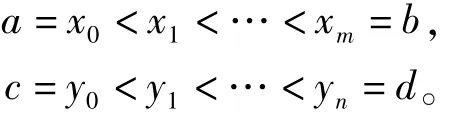
令ui（y），i=0，1，…，m，是定义在

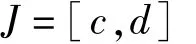
上的m+1个连续函数，满足插值条件

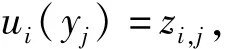
j=0，1，…，m。对于任意固定的y∈［a，b］，点集

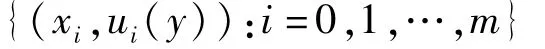
作为插值节点，根据上面的构造方法，能得到仿射分形插值函数gy（x），有

i=0，1，2，…，m。令

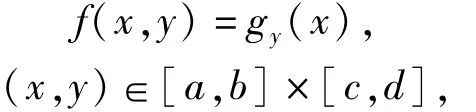
那么f（x，y）是［a，b］×［c，d］上的一个二元函数，并且满足插值条件

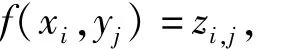
i=0，1，2，…，m，j=0，1，2，…，n。函数

（x，y）∈G的图象称为基于分形插值函数生成的分形插值曲面，文献［8］证明了f（x，y）是

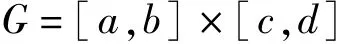
上的一个连续函数。

2 分形插值曲面的中心变差

令

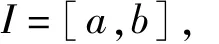
g（x）是I上的连续函数，对于一个非负实数γ和任意x∈I，设

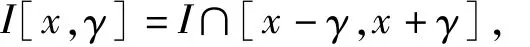
则称

是函数g（x）在点x的γ-中心振幅，简记为οg；γ（x）。因为g（x）是闭区间I上的连续函数，显而易见，οg；γ（x）在I上也是连续的，从而οg；γ（x）在I上可积，称οg；γ（x）在I上的积分

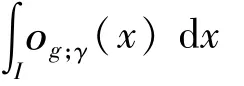
是函数g（x）在闭区间I上的γ-中心变差，记作Vg；γ（I）。

为了讨论构造的分形插值曲面的中心变差的性质，我们给出引理1。

引理11）若

t∈I，λ≠0，且g（x）是τ（I）上的连续函数，则

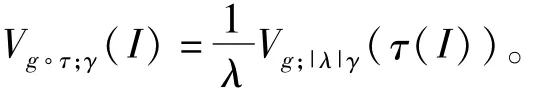
2）设g（x）是

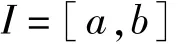
上的连续函数，

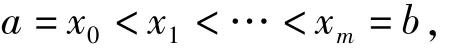
记

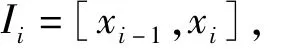
则

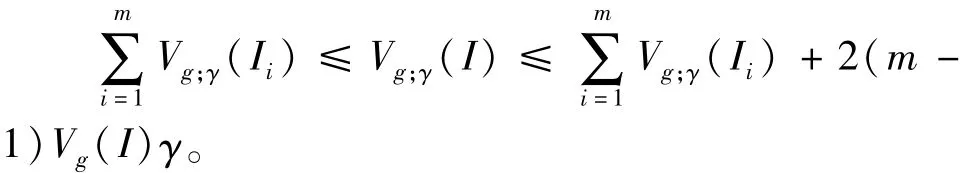
证明 1）设

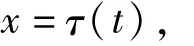
t∈I。因为

所以

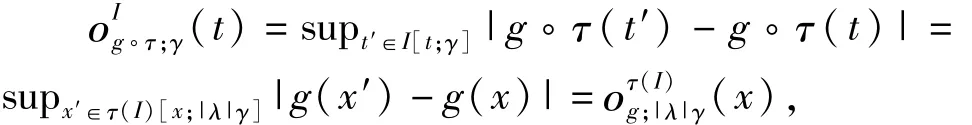
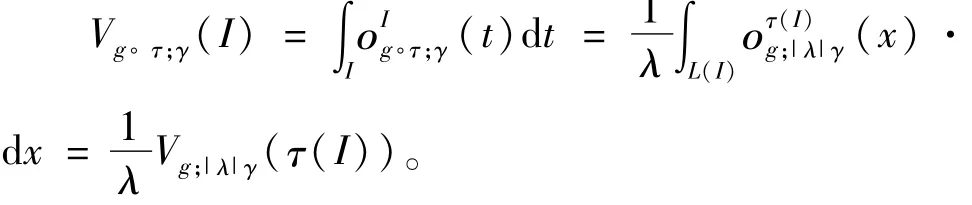
2）对于x∈Ii，因为

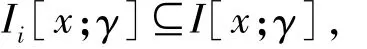
所以

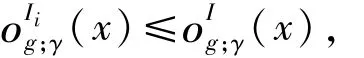
因此，方程左侧是成立的。接下来证明右侧。令

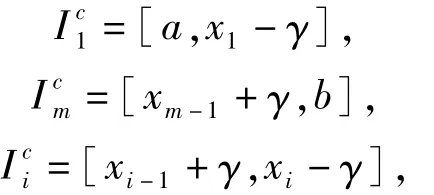
i=2，3，…，m-1，

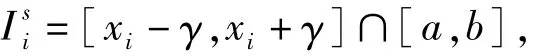
i=1，2，3，…，m-1，其中，当α＞β时，［α，β］就是空集。则

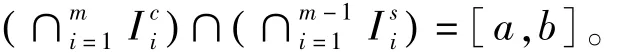
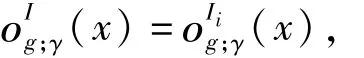
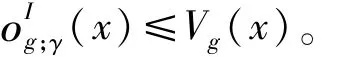
因此

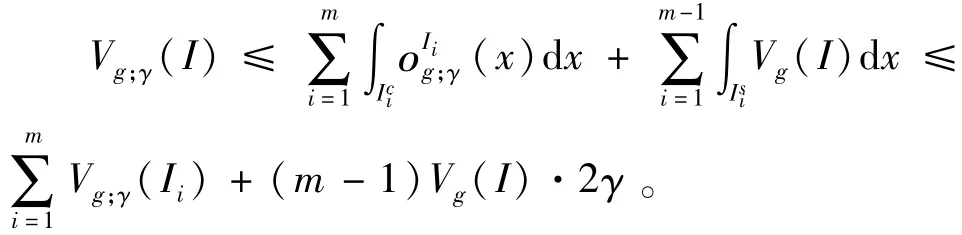
从而右侧不等式成立。

引理1证毕。

定理1对于构造的分形插值曲面

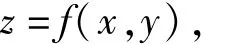
（x，y）∈D，存在正常数β1和β2，使得对于任意的γ≥0和y∈［c，d］，有

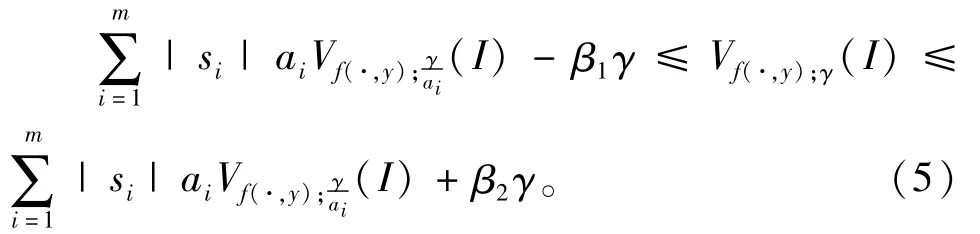
证明 因为f（·，y）是经过点集

的仿射分形插值函数，纵向尺度因子为

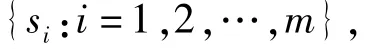
根据条件（4），对于xi∈Ii，有

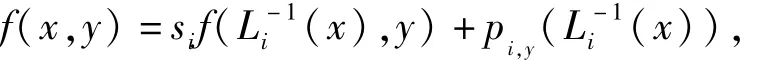
其中

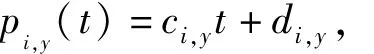
i=1，2，3，…，m。因为

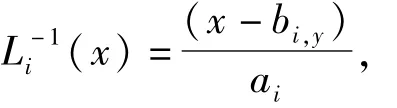
其中x∈Ii，根据引理1可得

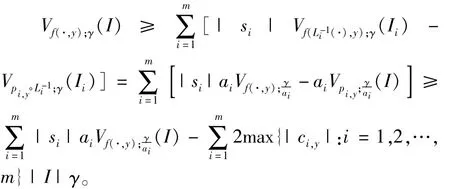
另一方面，根据引理1可以得到

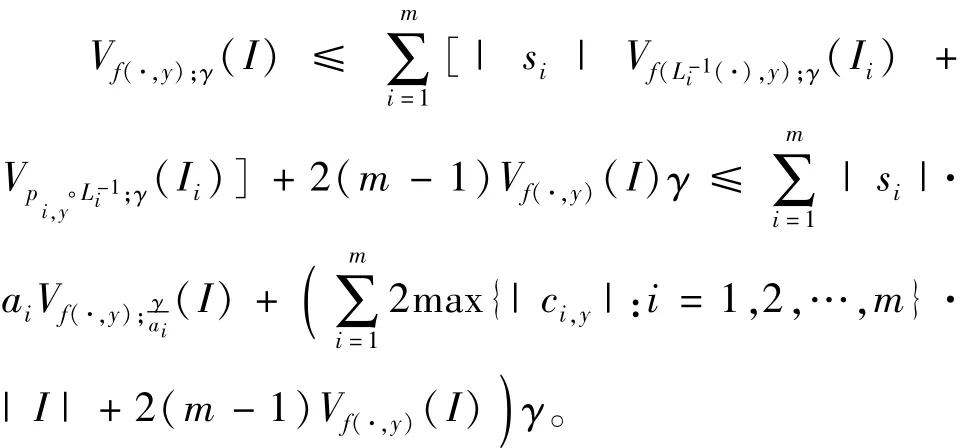
由映射（1）的系数计算可得

而ui在闭区间［c，d］上是连续的，因此，存在M＞0，当y∈［c，d］，i∈｛1，2，…，m｝时，使得

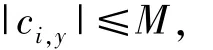
又因为

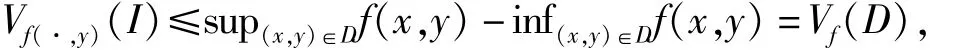
可以令

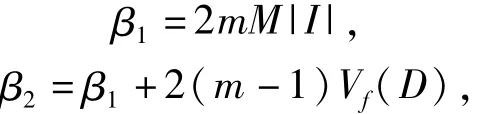
它们均与y，γ无关。

定理1证毕。

定理2设

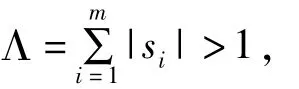
且对于任意的

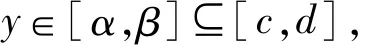
点集

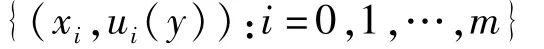
不共线，则存在常数C＞0，对于任意正整数k，以及任意y∈［α，β］和γ∈［0］，有

其中

证明对于确定的y∈［α，β］，设

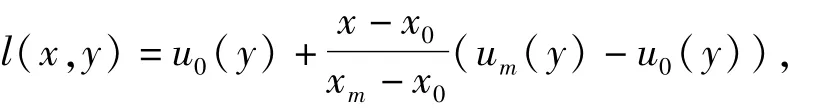
则l（x，y）在I上是线性函数，满足条件

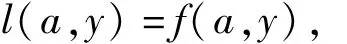
假设

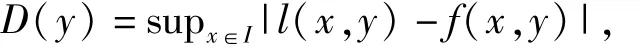
则D（y）在［α，β］上是正的连续的函数，因此

当y∈［α，β］，i1∈｛1，2，…，m｝时，令

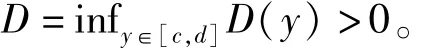
上是线性函数，且

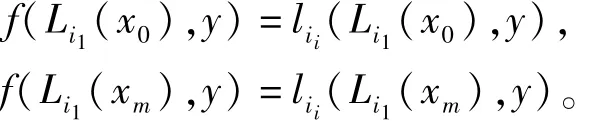
根据仿射分形插值函数的条件（4），

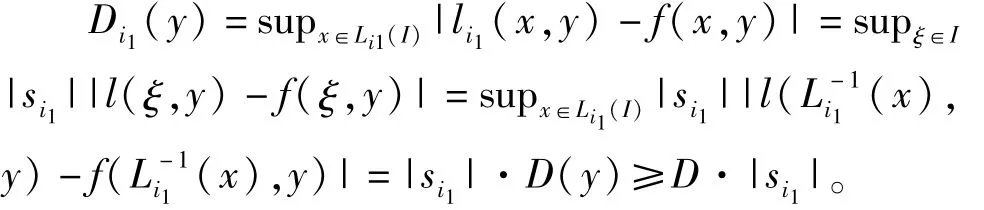
进而可以定义

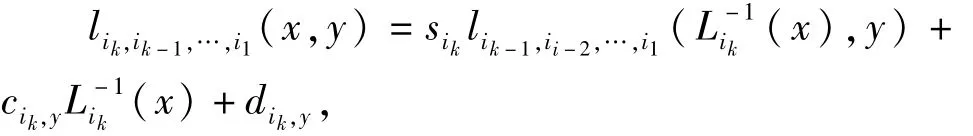
其中ik∈｛1，2，…，m｝，k=1，2，…。用数学归纳法可以证明lik，ik-1，…，i1（x，y）是区间Lik，ik-1，…，i1（I）上的线性函数，

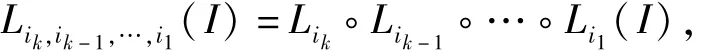
满足

并且有

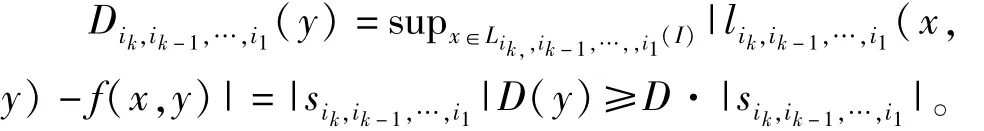
对于闭区间［t1，t2］上的连续函数g（t），若

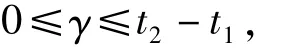
则有

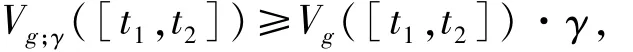
其中，

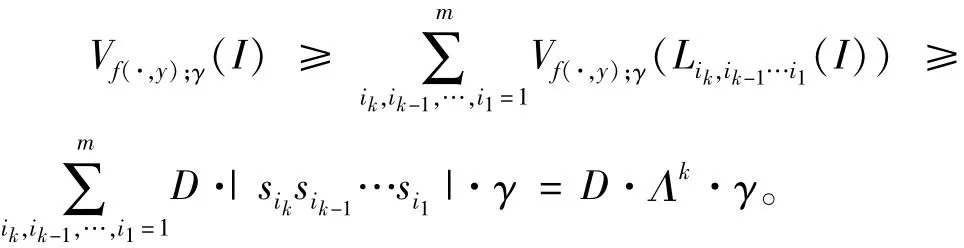
定理2证毕。

［1］BARNSLEY M F.Fractal functions and interpolation［J］.Constr.Approx.，1986（2）：303-329.

［2］BARNSLEY M F.Fractal everywhere［M］.New York：Academic Press，1988：17-28.

［3］XIE H，SUN H.The study on bivariate fractal interpolation functions and creation of fractal interpolated surfaces［J］.Fractal，1997，5（4）：625-634.

［4］XIE H，SUN H，JU Y，et al，Study on generation of rock fracture surfaces by using fractal interpolation［J］.Internet J.Solids Structures，2001（38）：5765-5787.

［5］DALLA L.Bivariate fractal interpolation functions on grids［J］.Fractals，2002，10（1）：53-58.

［6］FENG Z.Variation and minkowski dimension of fractal interpolation surface［J］.Math.Anal.Appl.，2008（345）：322-334.

［7］MALYSZ R.The minkowski dimension of the bivartiate Fractal interpolation surfaces［J］.Chaos，Solition and Fractal，2006（27）：1147-1156.

［8］BOUBOULIS P，DALLA L.Fractal interpolation surfaces derived from fractal interpolation functions［J］.Math.A-nal.Appl.，2007（336）：919-936.

〔责任编辑：卢 蕊〕

On central variation of fractal interpolation surfaces derived from fractal interpolation functions

SUN Xiu-qing
（Basic Courses Department，Zhenjiang Branch of Jiangsu Joint Vocational and Technical College，Zhenjiang 212016，China）

A construction method of fractal interpolation surfaces on a rectangular domain with arbitrary interpolation nodes is introduced.The variation properties of the bivariate functions corresponding to this type of fractal interpolation surfaces are discussed.

affine fractal interpolation function；fractal interpolation surface；central variation.

O241.3

A

1008-8148（2014）03-0044-04

2014-04-05

国家自然基金资助项目（51079064）

孙秀清（1978—），女，吉林松原人，讲师，硕士，主要从事数学分形插值函数研究。