一种基于信息熵的分布参数结构传感器／激励器优化布置方法

尹 涛

（武汉大学土木建筑工程学院，武汉 430072）

一种基于信息熵的分布参数结构传感器／激励器优化布置方法

尹 涛

（武汉大学土木建筑工程学院，武汉 430072）

针对用基于有限元方法的离散坐标体系研究传感器优化布置、所得仅为结构真实动力响应近似解直接影响传感器优化布置结果问题，提出基于贝叶斯统计系统识别方法与信息熵理论的分布参数结构传感器优化布置方法。以结构模型修正为目的，用贝叶斯统计系统识别方法识别结构模型参数最优值及不确定性程度，利用信息熵定量表征结构模型参数识别结果的不确定性程度；再将传感器优化布置问题转化为连续数值优化问题，以传感器位置为优化变量，通过遗传算法极小化模型参数识别结果的不确定性（即信息熵）识别传感器的最优布置位置；获得最大结构响应信息量，即识别结构模型参数的不确定性最小。通过双墩带弹性支撑的三跨连续梁桥数值仿真研究对该方法进行验证。

传感器优化布置；结构模型修正；贝叶斯统计系统识别方法；信息熵；遗传算法

传感器系统是构成结构健康监测系统的关键，传感器数目及其布置位置对实测数据的质量至关重要，其直接影响到基于动力测量信息的结构健康监测的成败。然而，目前传感器的布置大多仍基于经验，即通过考虑一系列实际约束条件来人为确定传感器布置位置，但这对于结构健康监测而言意义不大，因为这样无法保证所获得测量信息对于待识别结构建模参数的敏感性。因此，为保证所选传感器位置能获取足够的结构动力响应信息量，有必要开展传感器的优化布置问题研究。

传感器优化布置问题最先可能由Shah和Udwadia［1］在其研究工作中提出。后来，许多学者相继研究了基于结构模型参数及模态参数识别的传感器优化布置问题［2－7］。其中，Papadimitriou等［8］首次将信息学领域中的信息熵概念［9］引入到传感器优化布置问题研究中，用其来定量表征模型参数识别结果的不确定性程度，而传感器的最优位置则通过极小化该信息熵指标来给出，文章中研究了不同数量传感器与识别模态阶数对结构模型参数识别结果不确定性的影响。近来，该方法被Chow等人运用到了输电塔结构模型的传感器优化布置问题研究中［10］。

从目前文献资料来看，绝大多数传感器优化布置问题研究均是在有限元方法所建立的离散坐标体系基础上开展的。尽管离散坐标系统为分析任意复杂结构的动力响应分析提供了方便，但由于采用有限数目的位移坐标来描述结构体系的运动，所获得的解仅是结构真实动力特性的近似解［11］。虽然通过增加模型自由度数目，其分析结果的精度可获相应提高，然而，传感器优化布置问题属于结构动力学反问题范畴，通常需要采用数值优化方法来求解，但其目标函数通常具有高度非线性，求解获得收敛需要经过大量的迭代次数。增加模型自由度的方式将会使模型变得更复杂，并导致迭代求解时间花费大幅增加；同时，这也将使可布置传感器的待测自由度数目显著增加，更进一步地增加计算时间以及求解难度。基于这种考虑，用于传感器优化布置问题研究的离散坐标系统有限元模型网格划分通常很粗糙，这一方面增加了模型误差，另一方面也使感器可能布置位置局限于这些间隔较大离散节点上，且所获得的传感器最优布置位置与所采用的离散结构模型直接相关。此外，传统的基于有限元离散模型的传感器优化布置方法通常采用观测矩阵（包含若干0和1元素）将模型所有自由度映射到非常有限的测量自由度上，但每种传感器布置方案均需形成不同的观测矩阵，计算时间耗费较大。由此可见，对于具有典型分布参数特征的结构体系，采用连续坐标模型来进行传感器优化布置问题研究比采用基于有限元方法的离散坐标模型更具优势。

本文在Papadimitriou等［8］研究工作基础上，发展了一种基于信息熵和贝叶斯统计系统识别理论的分布参数结构系统的传感器优化布置方法，采用连续坐标结构体系来进行传感器优化布置问题研究。本文方法采用解析公式来构建分布参数结构体系，传感器布置位置采用连续坐标形式来表征，这也使本文方法与可布设传感器的待测自由度数目无关。先利用贝叶斯统计系统识别方法构建结构模型参数识别结果及相应不确定性程度的识别体系；再通过信息熵指标定量表征该不确定性程度来形成传感器优化布置目标函数；然后将传感器优化布置问题转化为带约束的连续数值优化问题，以传感器位置为优化变量，通过二进制编码遗传算法极小化信息熵指标，从而识别传感器的最优布置位置，即获得最大的结构响应信息量；最后，通过一个双桥墩带弹性支座的三跨连续梁桥模型的数值仿真研究对本文方法进行了验证。

1 理论背景

1.1 贝叶斯统计系统识别理论与信息熵

对于采用参数向量θ∈RNθ描述其输入输出特性的一类参数化结构模型M（Nθ代表参数向量θ的维数），在给定动力测量数据D条件下，文献［12］基于贝叶斯理论发展了一种可估计参数集θ均值及相应不确定性程度的统计系统识别方法。该方法假定识别误差同时服从空间和时间上独立、以及均值为0方差为σ2的正态分布，依据贝叶斯定理，在给定的实测数据D及模型类M条件下，结构模型参数及其预测误差参数集（θ，σ）的后验概率密度函数（PDF）可表示为：

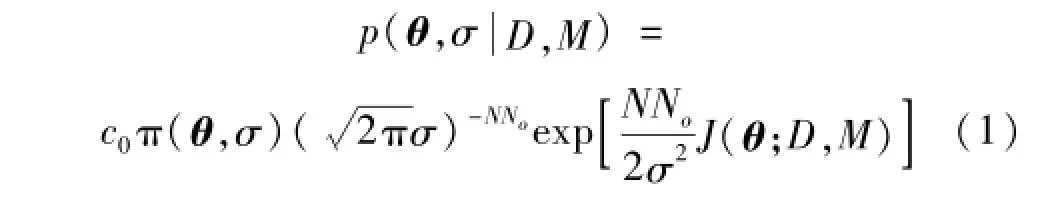
式中：c0表示使公式（1）等号右边积分为1的常数。π（θ，σ）表示参数集（θ，σ）的先验PDF。No和N分别表示测量点个数以及与之对应的采样时间点数。J（θ；D，M）表示实测响应与模型预测时程响应之间的吻合度函数，即：

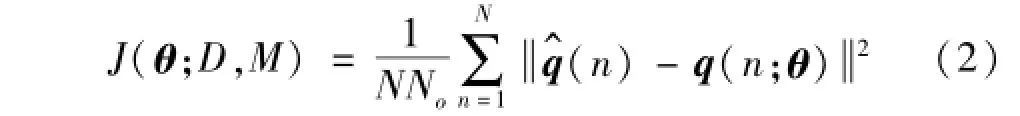
依据全概率定理，结构模型参数向量θ的后验边缘PDF可以通过公式（1）等号两边同时对σ进行积分得到，即

对于服从均匀分布的先验PDFπσ（σ），公式（3）等号右边关于σ的积分可以计算如下：

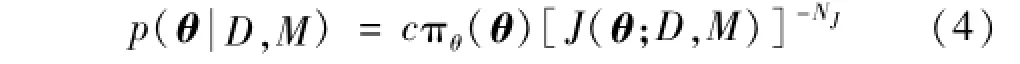
式中：NJ＝－（NNo－1）／2。c表示使公式（4）等号右边在给定积分域上积分为1的常数。

基于式（4）中计算出的后验PDF p（θ｜D，M），信息熵提供了结构模型参数θ估计值不确定性的标量量度［8］，即：

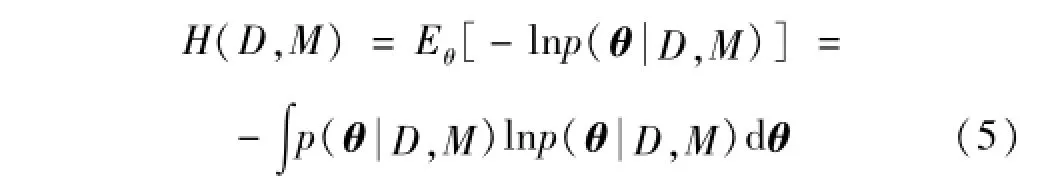
式中：Eθ表示关于参数θ的数学期望值。将式（4）代入式（5），可进一步得到：

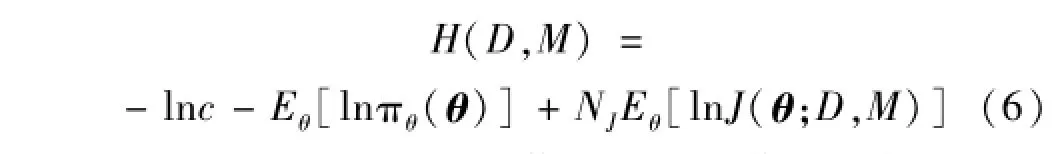
从式（6）中可以看出，信息熵的数值大小仅与实测数据D及所采用的模型类M有关。

为计算式（6）中由数学期望所产生的积分，运用Laplace渐近展开方法［13］得到信息熵在大量测量数据（即N→∞）条件下的渐进近似表达式［14］如下：

1.2 分布参数结构最优传感器／激励器布置

作为模型类M中结构参数θ识别结果不确定性程度的一个标量量度，公式（5）给出的信息熵H（D，M）本质上反映了实测数据D中含有用信息量的多少。从该意义上讲，传感器优化布置目的就是为了保证实测数据D对于参数集θ的信息量最大，即表示结构参数θ能以最小的不确定性被估计出来。换句话说，最优传感器布置方案应使信息熵极小化，即通过一个数值优化过程，实现信息熵相对于传感器布置位置的极小化。

然而，在进行传感器布置设计时，由于实测数据D是未知的，因此信息熵H（D，M）中应该去掉对实测数据D的显式依赖。注意到在获得大量实测数据（N→∞）前提下，将信息熵定义在最优模型参数值θ＾与相应最优预测误差处，可以渐进近似地去除其与实测数据的显式相关性，但在无实测数据情况下，最优模型参数值与相应最优误差估计值同样也是无法获知的。为了解决这个问题，文献［14］建议采用某些能较合理反映系统特性的标称参数来取代未知的最优值。在这种情况下，针对分布参数结构系统，本文提出由公式（7）给出的信息熵可进一步表示如下：

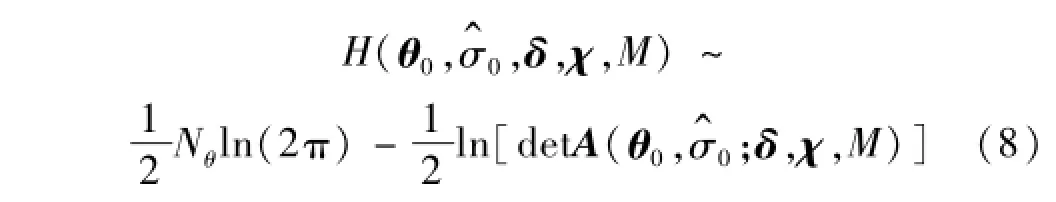
式中：δ＝｛δ1，δ2，…，δNo｝T∈RNoND表示传感器布置向量，其包括所有测点的坐标值。det［·］表示对矩阵取行列式运算符。对于多输入多输出系统，类似地，所有的激励点坐标采用χ＝｛χ1，χ2，…，χNI｝T∈RNIND来表示，NI表示激励点数，而δk∈RND（k＝1，2，…，No）与χI∈RND（l＝1，2，…，NI）分别表示第k个测量点与第l个激励点的无纲量坐标。ND表示目标结构模型的空间维数，具体地，ND＝1，2，3分别表示一、二及三维目标结构。

经推导，公式（8）中的A（θ0，σ＾0；δ，χ，M）可以渐进近似为（N→∞）

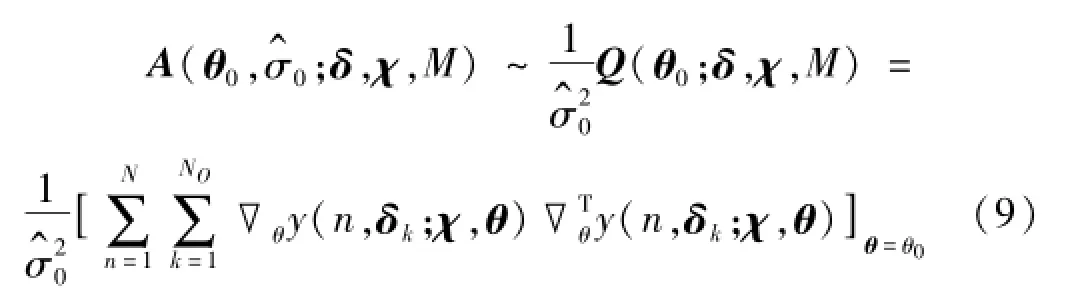
式中，▽θ＝［∂／∂θ1，∂／∂θ2，…，∂／∂θNθ］T表示相对于参数集θ的梯度向量。y（n，δk；χ，θ）表示公式（2）中给出的模型计算响应向量q（n；θ）的第k个元素，其代表第n个时间步上第k个测量点处所计算的时域响应。因此，公式（8）可以进一步地表示为：

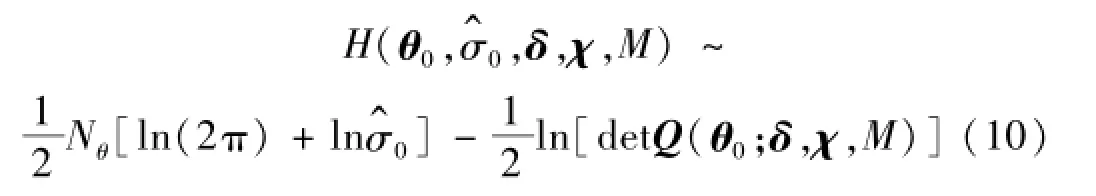
从上式可以很明显地看出，极小化信息熵等价于极大化半正定对称矩阵Q（θ0；δ，χ，M）的行列式。应该指出，本文所研究的是冲击荷载响应，若对于环境激励的情况，通常无法获知激励点位置，因而此时信息熵公式中不再包含荷载位置向量χ。

2 数值仿真研究

2.1 传感器／激励器优化布置

为了验证本文所提出的分布参数体系传感器优化布置方法在桥梁结构上的应用，本文以一个双桥墩带弹性支撑的三跨等截面连续梁桥比例模型为例进行验证，如图1所示。

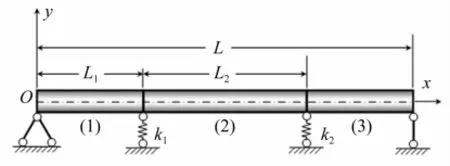
图1 两桥墩带弹性支撑的三跨连续梁桥模型Fig．1 Three-span continuous bridge modelwith elastic supports at two piers

该桥梁模型总长L＝2．3 m，两边跨长均L1＝0．65 m，中跨长L2＝1．0 m；主梁截面宽度b＝0．01 m，高度h＝0．02 m，弹性模量E＝5．8×1010N／m2，质量密度ρ＝为沿主梁纵向单位长度质量；＝EI为主梁抗弯刚度，I为截面惯性矩。设两桥墩与桥面联接处均布置竖向弹性支座，弹簧刚度k1＝k2＝2．0×106kN／m。为简便，引入无纲量坐标ζ＝x／L，即两弹性支撑位置分别为ζ1＝L1／L，ζ2＝（L1＋L2）／L。传感器位置δ与激励器位置χ均用无纲量坐标形式表示。

对该三跨连续梁桥，拟采用7个无纲量建模参数θk（k＝1，…，Nθ，Nθ＝7）分别修正全桥各跨的抗弯刚度（DE，0）、全桥单位长度质量、两桥墩处的竖向弹簧刚度以及用于动力响应计算的模态阻尼比（ξD，0），如表1所示。其中以及ξD，0分别表示初始的建模参数值表示第j个弹性支座的无纲量弹簧刚度。为消除结构对称性影响，第一跨抗弯刚度取为1．05 DE，0。本算例假定所有阶模态均采用一致的阻尼比。因此，修正后的结构参数分别为2）以及ξD＝θ7ξD，0。假定模型参数修正量较小，因此无纲量模型参数θ的标称值θ0可以取为1，即θ＝ones（Nθ，1）。考虑单点竖向冲击荷载作用，采用前4阶模态参数并运用模态迭加法计算分布参数系统的加速度时程响应，同时假定所有阶模态的阻尼比均取为1%。其中，采样频率取为1 000 Hz，采样时间为0．5 s。

表1 本文算例考虑的模型修正参数Tab.1 Modeling parameters considered for structuralmodel updating

与传统基于离散坐标体系的传感器优化布置方法不同，本文方法将传感器优化布置问题转化为带边界约束的连续数值优化问题。对于此类优化问题的求解，尽管目前存在一些标准的基于梯度信息的数值优化算法，但此类算法容易陷入局部极小，同时也非常依赖于初始解的选取。而基于人工智能的遗传算法较传统的基于梯度的优化算法具有更强的全局优化能力，因此本文选用遗传算法进行传感器优化布置问题研究。其中，遗传算法采用二进制编码，单个变量的编码长度为Nbits，其将求解域等分为2Nbits－1段，或求解精度为1／（2Nbits－1）。通过改变编码长度，可以直接改变求解域划分的疏密（也即待布置传感器位置个数），这就可以很方便地研究传感器优化布置结果受待布置位置个数的影响。值得指出的是，当Nbits＝10时，传感器布置位置精度接近1．0×10－3。

表2表示本文方法所识别出的传感器与激励器最优布置结果。其中，分别考虑了3种不同的二进制编码长度（即Nbits＝4、8以及10）以及4种不同的传感器数目（NO＝1～4）。从该表中可以很明显地看出，随着传感器数目逐渐增加，目标函数ln（det Q）值逐渐增加，即信息熵指标逐渐降低（根据公式（10））。这表明增加传感器数目可以获得较大的信息量，从而降低模型参数识别结果的不确定性。另外，在模态叠加法中通过增加更多阶的模态参数，也将获取更多的信息，从而减少待识别参数识别结果的不确定性，限于篇幅关系本文未予给出。

从表2中也可以看出，当仅使用单个传感器时，不管Nbits取值如何，识别的最优激励器位置总与传感器位置相同，该结论符合Maxwell互易定理。但当使用的传感器数目多于1个时，所识别的最优激励器位置并不总是包含在最优传感器位置集中。例如，当Nbits＝8且考虑2个传感器时，识别的最优激励器位置为0．1216，其与该工况第1个传感器最优位置相同。当NO＝3，即考虑3个传感器时，所识别的最优激励器位置不变，但是其并不与该工况下任何一个最优传感器位置相重合。另一方面，从表2中还可以看出，考虑n个传感器时的最优传感器位置集并不一定包含于n＋1个传感器时的最优位置集中。例如，当Nbits＝8时，考虑2个传感器情况下，所识别出的传感器最优位置分别为0．121 6和0．125 5。但当考虑3个传感器时，所识别的最优传感器位置分别是0．125 5，0．129 4和0．603 9，很明显NO＝2时的最优传感器位置0．1216未被包含NO＝3时的结果集中。以上结论与基于有限元方法的离散结构系统所获得的结论相吻合［10］。

表2本文方法所识别的传感器／激励器最优布置位置Tab.2 Optimal sensor and excitation locations identified by the proposed method

此外，从表2中还可以看出，所识别的某些传感器最优位置很接近，尤其是当二进制编码位数取较大值时，例如Nbits＝8和10。以Nbits＝8时的传感器优化布置结果为例来说明，当采用2个传感器时，传感器最优位置之差约为0．0039；当采用3个传感器时前两个传感器的最优位置之差也为0．003 9，而4个传感器情况下前3个之间的距离同样如此。注意到Nbits＝8时遗传算法求解精度为1／（28－1），其值约为0．003 9，由此可以推断，当NO＝2、3、4情况下，最优位置接近的传感器之间的布置距离差已达到当前二进制编码长度下的最大分辨率。Nbits＝10时的情况与Nbits＝8时的类似。

2.2 结构建模参数识别

为了更进一步验证本文方法，在前一阶段获得了传感器／激励器最优布置之后，此阶段基于贝叶斯统计系统识别方法进行了桥梁建模参数及其不确定性识别研究，所考虑的工况如表3所示，并取Nbits＝10。共八种工况，其中，前四种为传感器／激励器布置于最优位置工况（即为表2中的识别结果），设置这四种工况主要是考查传感器数目NO对桥梁建模参数识别结果不确定性程度的影响。后四种工况为传感器数目取4、传感器／激励器布置于任意非最优位置时的工况，该系列工况主要用以研究传感器布置位置对于识别结果不确定性程度的影响。表3考虑的八种工况中，用于计算加速度时程响应的控制参数与传感器／激励器优化布置阶段相一致。

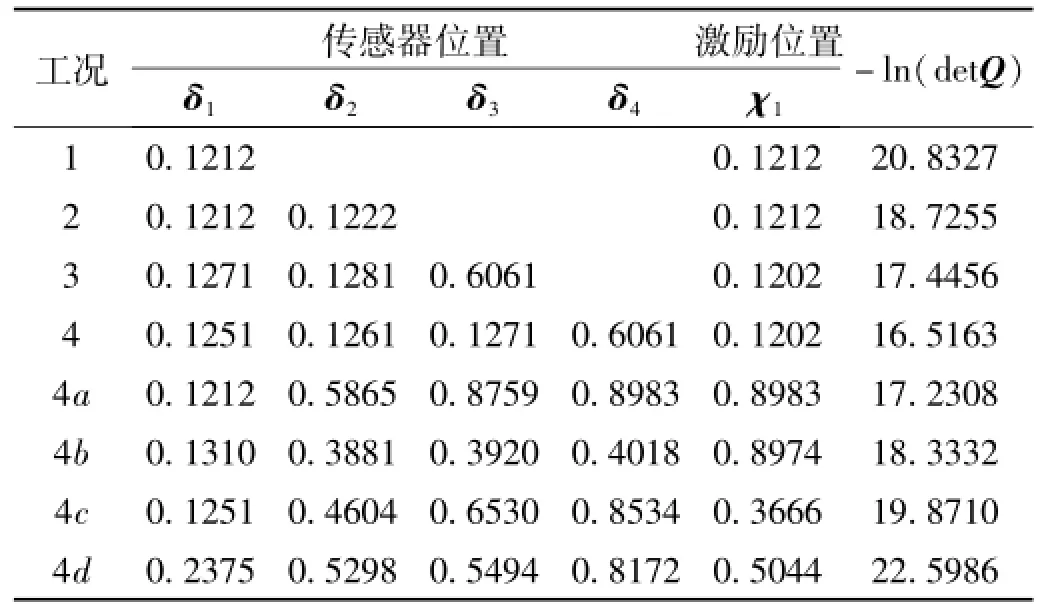
表3 三跨连续梁桥模型参数识别中所考虑的传感器／激励器布置工况（Nbits＝10）Tab.3 Cases of sensor and excitation locations considered for them odeling parameter identification of the three-span continuous bridgemodel（Nbits＝10）

图2表示传感器／激励器布置于最优位置（工况4）与任意位置（如工况4d）时，各测量通道加速度功率谱密度函数比较，该对比结果可以定性表征传感器／激励器布置位置对于采集信号的影响。对比两种工况，可以很明显地看出，传感器／激励器布置于最优位置时，各测量通道所采集信号的频率成份均很丰富，即在0到300 Hz的频带范围内，均清晰识别出了参与模态叠加的前4阶频率。而布置于工况4d中的非最优位置时，很明显第2阶频率基本上没被识别出来；同时各测量通道所包含的频率信息也不太一样，且均未完整测出前4阶模态，有的仅漏掉了第2阶频率（如第2、3与4个传感器通道），有的则同时漏掉了第2和第4两阶频率（如第1个传感器通道）。由此可见传感器优化布置对数据采集的影响较大，进而可初步预见工况4中模型参数识别结果的不确定性将低于工况4d中的相应结果，这一点将在后面参数识别结果中得到验证。

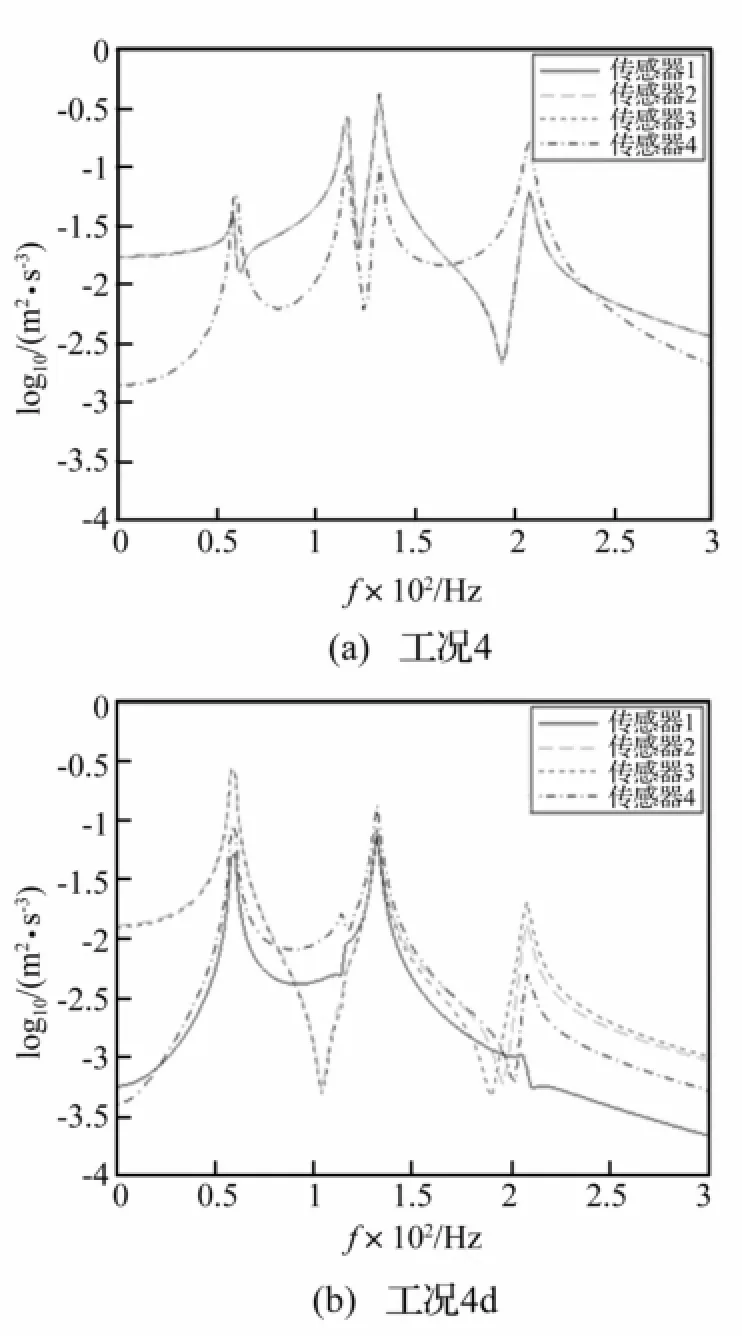
图2 传感器／激励器布置于最优位置、任意位置时各测量通道加速度功率谱密度函数对比Fig．2 Acceleration spectral density functions for four sensors located at their optimal and arbitrary non-optimal positions

为了模拟实际条件下测量噪声的影响，此参数识别阶段中加速度响应计算值考虑了10%的高斯白噪声。表4给出了相应于表3中所列各工况的模型参数识别结果，其中，各工况的识别值代表模型参数识别结果的最优值，而COV（%）值则代表参数识别结果的变异系数，即不确定性程度，并以百分数来表示。对比前四种工况中的COV值，从该表中可以明显看出，随着传感器数目NO的增加，COV值逐渐降低，表明采用较多的传感器，确实能使所获取的测量信息总量增加（参考表3中最后一列给出的目标函数值大小），从而减少结构模型参数识别结果的不确定性程度，这同时也验证了本文所提出的传感器／激励器优化布置方法的正确性。

对比工况4与其后四种工况的COV值，可以发现，在给定传感器数目NO条件下，传感器布置于最优位置相比于其他非最优位置，所识别出的模型参数的不确定性程度整体上确实较低，这也验证了前面图2中的相关结论。另外，比较工况4a至工况4d的COV值可以发现，在四种任意选取的非最优位置中，工况4a参数识别结果的不确定性程度相对最低，而工况4d的不确定性则最高，该现象与第一阶段传感器／激励器优化布置过程中表3最后一列给出的各工况目标函数值是相吻合的，即目标函数值越大，同条件下模型参数识别结果的不确定将越小。

另外，值得注意的是，对比表4中工况3和工况4a至4d的COV值识别结果可以看出，当采用3个传感器与相应激励器布置在其最优位置，相比4个传感器与相应激励器任意布置，可获得更小的模型参数不确定性。特别地，参照工况1的结果还可以发现，当仅采用单个传感器时，通过优化布置传感器与相应激励器位置，也可望使模型参数识别不确定性与采用4个传感器情况下的结果相当。这充分说明了传感器优化布置对于模型参数识别的重要性。

此外，从表4中各工况单个模型参数的相对不确定性程度来看，θ5和θ6的不确定性程度较其余5个参数明显要大很多。参考表1中的桥梁建模参数定义，这两个参数分别对应于两个桥墩的弹性支撑刚度，这表明弹性支撑刚度参数的识别精度较其余参数明显偏低。这与文献［15］中关于某悬臂梁固定端半刚性连接的转动刚度识别实验室模型试验结果相吻合，在该文献中，作者研究表明固定端转动刚度识别结果的不确定性较其余建模参数大许多。其实，这一点从本文模型参数识别结果的精度上也可以得到一定程度的体现。具体地，参照表4，分别对比各工况中单个模型参数的识别值，可以明显发现，θ5和θ6的识别结果精度相对于其余参数较差。应该指出，本文算例以θ0＝ones（7，1）作为基准参数，计算加速度响应信号并施加高斯白噪声以模拟测量信号，因而将θ0作为θ的精确值。

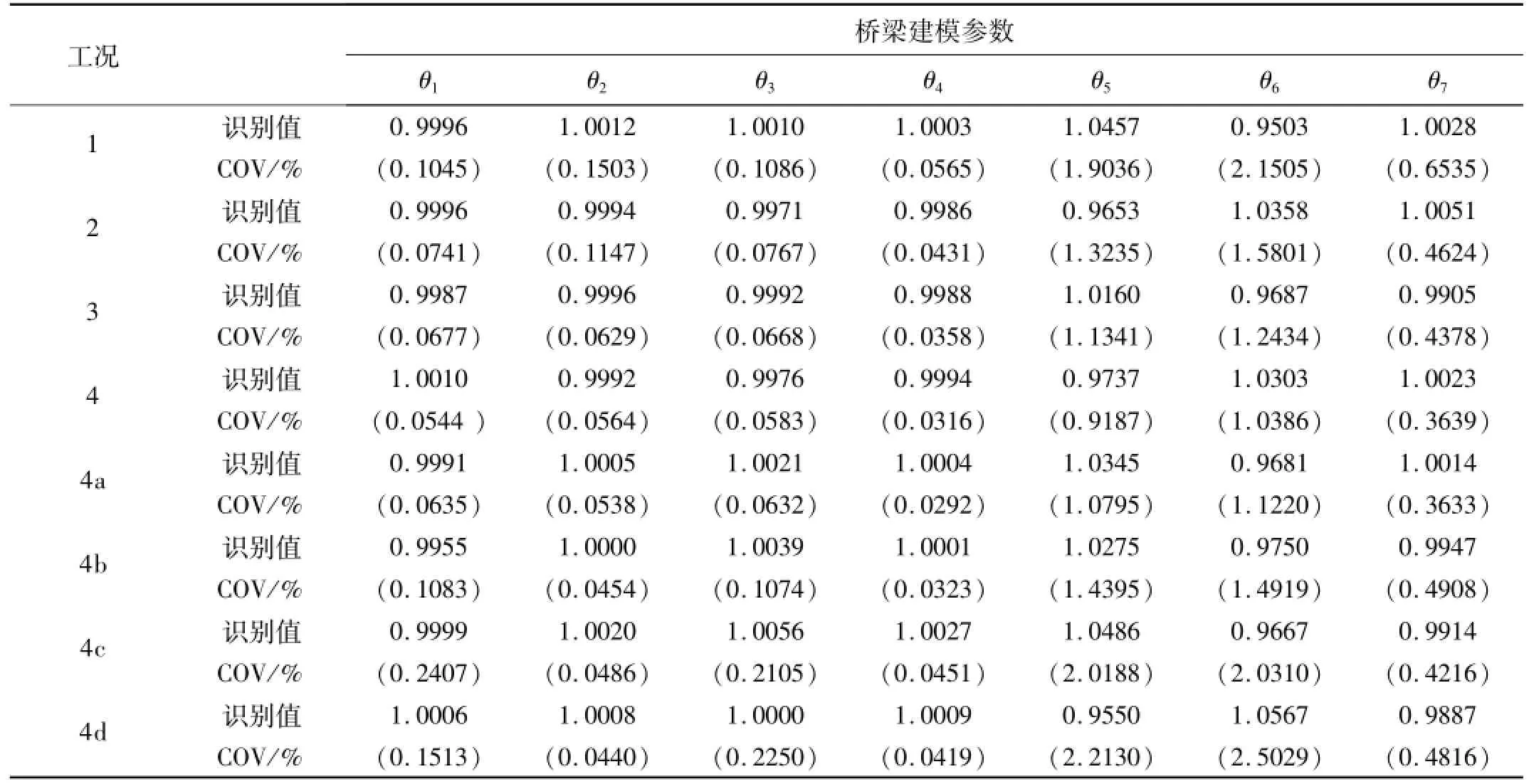
表4 三跨连续梁桥模型参数识别结果及变异系数（COV值）Tab.4 Optimal values and associated coefficient of variances（COV）of identified modeling parameters for three-span continuous bridgemodel

为了更直观地表示各参数识别结果之间的不确定性，本文选取工况4中部分建模参数，利用公式（3）计算其识别结果的二维边缘PDF，并对其进行归一化，结果如图3所示。其中，图3（a）、图3（b）分别表示θ5与θ6之间、以及θ3与θ5之间的二维归一化边缘PDF分布。从图3（a）中可以明显地看出，θ5与θ6之间的不确定性程度大致相同。这一点也可以从表4中的有关结果中得到印证，因为从该表得出工况4中θ5与θ6的COV值分别为0．918 7与1．038 6，其数值上基本相同。对于θ3与θ5而言，图3（b）中曲面形状可以明显反映出两参数之间的相对不确定性程度，即θ5的不确定性要远大于θ3的不确定性，其也与表4的有关结果相吻合。

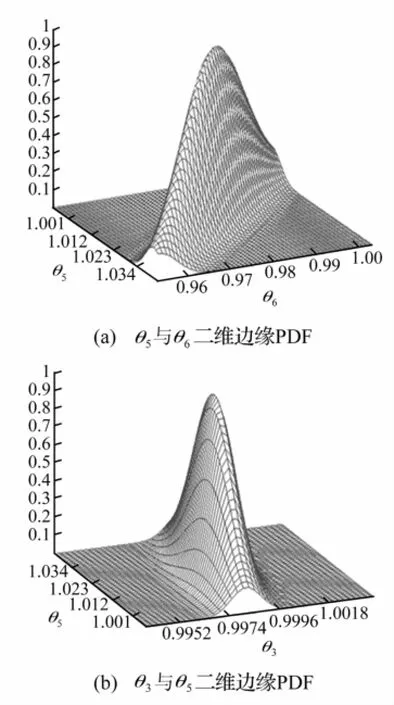
图3 工况4部分建模参数识别结果的二维归一化边缘PDFFig．3 Normalized PDFs of some selected parameters in case 4

3 结 论

针对分布参数结构体系的传感器优化布置问题，本文提出了一种以结构模型修正为目的的传感器／激励器优化布置方法。该方法将贝叶斯统计系统识别方法与信息熵理论相结合，通过信息熵定量表征结构模型参数识别结果的不确定性程度，并采用遗传算法极小化该不确定性以实现传感器／激励器最优布置，以期获得最大的结构响应信息量，并使识别出的结构模型参数不确定性最小。

文中以一个双桥墩带弹性支撑的三跨连续梁桥模型为例，通过一系列数值仿真工况，先后对传感器／激励器优化布置以及模型参数识别相关问题进行了仿真研究，并对本文方法进行验证。研究结果表明，本文方法能同时识别分布参数结构体系给定数目的传感器与激励器最优布置位置；传感器数目对于最优化布置结果及模型参数识别结果均有较大的影响，即采用较多数目且经过优化布置的传感器可以减少模型参数识别结果的不确定性；经过优化布置的较少数目传感器可获得与较多数目任意布置传感器相同甚至更小的模型参数不确定性；就本文算例而言，桥墩弹性支撑刚度参数识别结果的不确定性较其他参数大得多，这一点在实际桥梁建模及分析过程中应予以注意。

应该指出，本文方法为典型分布参数结构体系的传感器优化布置问题提供了解决思路，但对于其他任意复杂结构体系而言，基于有限元方法的离散结构模型则更适合。此外，从表2的识别结果中可以推断，随着遗传算法中二进制编码位数增加，算法的最大分辨会随之提高，进而使某些相互靠近的最优传感器之间布置距离进一步减小，但在实际应用中布设空间上如此接近的传感器却不太可行。而这种现象在传统的基于有限自由度离散模型的传感器优化布置研究结果中通常难以观察到（其对应本文Nbits取较小值情况，如4），除非网格化分足够细密。因此，本文研究表明，对于分布参数结构体系仅极大化ln（det Q）该单一目标函数似乎不够，有必要对其进行改进，从而避免传感器最优识别位置过于接近。

［1］Shad P，Udwadia F E．A methodology for optimal sensor locations for identification of dynamic systems［J］．Journal of Applied Mechanics，Transactions of the ASME，1978，45（1）：188－196．

［2］Kammer D．Sensor placements for on orbit modal identification and correlation of large space structures［J］．Journal of Guidance Control and Dynamics，1991，14（2）：251－259．

［3］Udwadia F E．Methodology for optimal sensor locations for parameters identification in dynamic systems［J］．Journal of Engineering Mechanics，1994，120（2）：368－390．

［4］Penny JE T，Friswell MI，Garvey SD．Automatic choice of measurement location for dynamic testing［J］．AIAA Journal，1994，32（2）：407－414．

［5］何浩祥，闫维明，张爱林．面向结构健康监测的传感器数量及位置优化研究［J］．振动与冲击，2008，27（9）：131－134．

HE Hao-xiang，YANWei-ming，ZHANG Ai-lin．Optimization of number and placement of sensors for structural health monitoring［J］．Journal of Vibration and Shock，2008，27（9）：131－134．

［6］卢伟，滕军．基于数据融合的传感器优化布置方法［J］．振动与冲击，2009，28（9）：52－55．

LUWei，TENG Jun．A method of optimal sensor placement based on data fusion［J］．Journal of Vibration and Shock，2009，28（9）：52－55．

［7］刘伟，高维成，李惠，等．基于有效独立的改进传感器优化布置方法研究［J］．振动与冲击，2013，32（6）：54－62．

LIUWei，GAO Wei-cheng，LI Hui，et al．Improved optimal sensor placement methods based on effective independence［J］．Journal of Vibration and Shock，2013，32（6）：54－62．

［8］Papadimitriou C，Beck J L，Au S K．Entropy-based optimal sensor location for structural model updating［J］．Journal of Vibration and Control，2000，6（5）：781－800．

［9］Jaynes E T．Where do we stand on maximum entropy？The Maximum Entropy Formalism，Levine R D and Tribus Meds［M］．Cambridge：MIT Press，1978．［10］Chow H M，Lam H F，Yin T，Au S K．Optimal sensor configuration of a typical transmission tower for the purpose of structuralmodel updating［J］．Structural Control and Health Monitoring，2011，18（3）：305－320．

［11］Clough RW，Penzien J．Dynamics of Structures（3rd）［M］．Computers and Structures，Inc．，Berkeley，C A，2004．

［12］Beck J L，Katafygiotis L S．Updating models and their uncertainties-Bayesian statistical framework［J］．Journal of Engineering Mechanics，1998，124（4）：455－461．

［13］Bleistein N，Handelsman R A．Asymptotic expansions for integrals［M］．Dover Publications，Inc．，New York，N Y，1986．

［14］Papadimitriou C．Optimal sensor placementmethodology for parametric identification of structural systems［J］．Journal of Sound and Vibration，2004，278（4／5）：923-947．

［15］Lam H F，Ng C T，VeidtM．Experimental characterization of multiple cracks in a cantilever beam utilizing transient vibration data following a probabilistic approach［J］．Journal of Sound and Vibration，2007，305（1／2）：34－49．

Probabilistic approach for optimal sensor／actuator configuration of distributed-param eter system s based on in formation entropy

YIN Tao
（School of Civil and Architectural Engineering，Wuhan University，430072Wuhan，China）

For distributed-parameter systems，the continuous-coordinated models are more suitable than the conventional FE-based discrete-coordinated models for investigating the optimal sensor placement problems．For the purpose of structuralmodelupdating，a sensor／actuator configurationmethodology for the distributed-parameter system was developed based on both the Bayesian statistical system identification method and information entropy．In the proposed methodology，the Bayesian statistical system identification method was adopted to identify the optimal values and associated uncertainties of the structuralmodeling parameters，whereas the information entropy was employed as a scalar measure to quantify the uncertainties．Then，the problem of optimal sensor／actuator placement was formulated as a continuous optimization problem，in which the information entropy wasminimized by using the genetic algorithm，with the sensor／actuator configurations as theminimization variables．Maximum amountof information about the structuralmodeling parameterswould be obtained if the sensors／actuators are placed at their optimal locations，indicating the uncertainties of identified modeling parameters being minimum．The proposed methodology was verified through a set of numerical simulation cases for a three-span continuous bridgemodelwith two elastic supports at the top of piers．

optimal sensor configuration；structural model updating；Bayesian statistical system identification method；information entropy；genetic algorithm

O211；O321

：A

10．13465／j．cnki．jvs．2014．22．010

国家自然科学基金资助项目（51208390）；湖北省自然科学基金资助项目（2011CDB265）；中央高校基本科研业务专项经费资助项目（271198，273766）

2013－08－07 修改稿收到日期：2013－09－27

作 者尹涛男，博士，副教授，1979年12月生邮箱：tyin＠whu．edu．cn