一种薄壁壳体零件的静力仿真和静力试验

吕忠卫, 顾 峰, 戴秀芬

（上海无线电设备研究所,上海 200090）

一种薄壁壳体零件的静力仿真和静力试验

吕忠卫, 顾 峰, 戴秀芬

（上海无线电设备研究所,上海 200090）

利用有限元对薄壁壳体进行静力学分析,并采用实物试验对仿真结果进行验证,建立了薄壁壳体零件设计和静力学分析的方法。

壳体；静力仿真；静力试验

0 引言

当前对机械类产品的设计要求是轻、巧、小,并在此基础上具有相当的力学要求,能满足产品的强度指标。这就要求在产品的开发设计时做相应仿真分析和实物静力学试验,以此提高设计的可靠性,节约研制成本和缩短研制周期。

1 零件设计

零件在初步设计阶段就需要考虑产品的技术指标要求,从而选择相应的材料以及采用相应的设计来满足技术指标要求。

1.1 指标要求

对某圆柱壳体类零件,总体给出如下指标：

a）壳体重量小于350 g。

b）壳体在承受3 950 N剪力时,能同时承受1 352 Nm的弯矩,安全系数为1.5。

c）壳体长度为112 mm,直径为127 mm。

1.2 壳体的设计

按照重量指标和力学要求,选择铝合金2A12-T4作为该零件的材料。表1为该材料的物理属性。

零件设计时,充分考虑力学要求,在减重的同时,局部采用加强筋以提高壳体的力学性能。

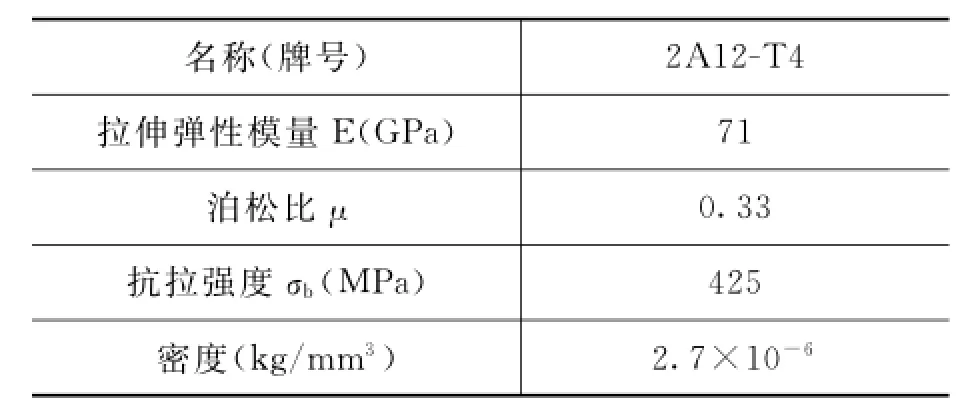
表1 零件材料属性

如图1所示,壳体壁厚为2 mm,局部采用4 mm厚加强筋增加壳体强度。经分析,该零件重量为334 g,满足指标要求。

图1 壳体三维造型

2 静力学仿真

在完成壳体的结构设计以及材料选择后,须对该壳体进行静力学分析,校核其强度是否能满足指标要求。

2.1 壳体有限元模型

壳体上的许多小孔对整个舱体的强度和刚度的影响较小,因此在有限元建模过程中把这些小孔去除不予考虑。建好的壳体有限元模型如图2所示,模型中采用十节点四面体二阶实体单元。

图2 壳体有限元模型

2.2 施加载荷及约束条件

在有限元软件中较难直接模拟总体所给出的条件,因此在建模过程中通过等效弯矩计算,对壳体进行适当延长便于加载。

通过等效计算,把壳体总长加长至366 mm,其中一端（用于加载载荷）延长238 mm,另一端（用于加载约束）延长16 mm,在延长后的端面上施加3 950 N的载荷就能够模拟产生最大弯矩为1 382.5 N·m的弯矩。考虑到安全系数为1.5,须在载荷施加面施加5 925 N的剪力,同时在壳体另一端面将产生2 073.75 N·m的弯矩。

图3为壳体的载荷与约束图,图中左端面加载了5 925 N的载荷,右端面进行了六自由度的约束。

图3 壳体载荷与约束图

2.3 计算结果

采用ANSYS软件对图3进行有限元分析,壳体的应力云图如图4所示,可以看出壳体的最大应力位于壳体右端面退刀槽处,大小为315 Mpa,低于材料的抗拉强度为425 Mpa,表明该壳体的设计能满足力学指标要求,且剩余强度系数为1.349。

3 壳体静力试验

为了进一步验证所设计薄壁壳体的力学性能,需要对实物进行静力试验。

3.1 试验条件设置

图4 壳体的应力云图

从仿真结果可以得到,壳体在承受150%的使用载荷时,尚剩余强度系数为1.349,因此在实物静力试验中,设定试验载荷为使用载荷的150%,即加载5 925 N的剪力,该剪力将在壳体另一端面产生2 073.75 N·m的弯矩。图5为该壳体静力试验加载示意图。

壳体静力由固定板、转接环、壳体（试验件）、位移计、加力环和接长筒组成。固定板与转接环的作用是固定壳体,位移计的作用是测量壳体在加载情况下的位移变化量,接长筒的作用是使过载加载在图5所示366 mm处,加力环的作用是在试验环Q处进行力的加载。

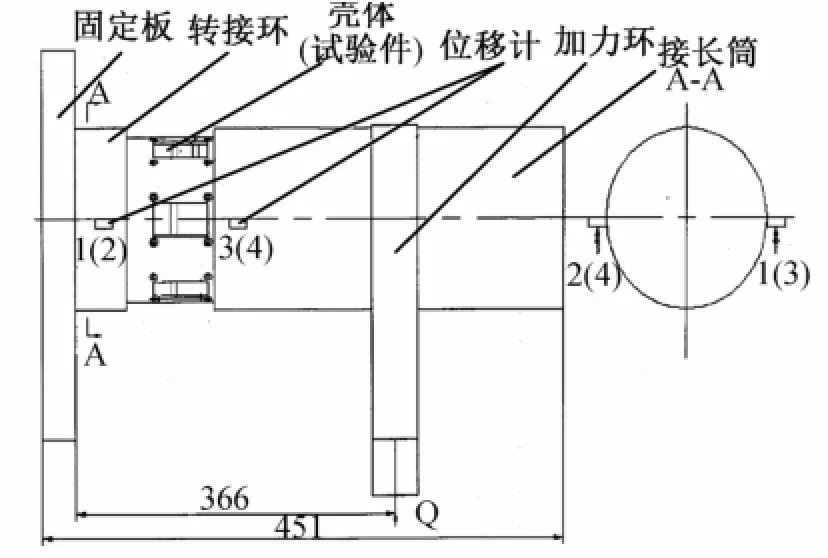
图5 壳体静力试验加载示意图

如图5所示,在壳体后端固定有两只位移计,分别是1#和2#,在壳体前端也固定有两只位移计,分别是3#和4#。

试验时,在Q处以试验载荷的10%为一级,逐级加载,直至加载至100%试验载荷（即150%使用载荷）后卸载,查验在各级载荷作用下位移的变化量。

3.2 试验结果

试验结果如表2所示,1#位移、2#位移、3#位移和4#位移分别对应1#位移计、2#位移计、3#位移计和4#位移计在相应载荷时所测量的位移值。

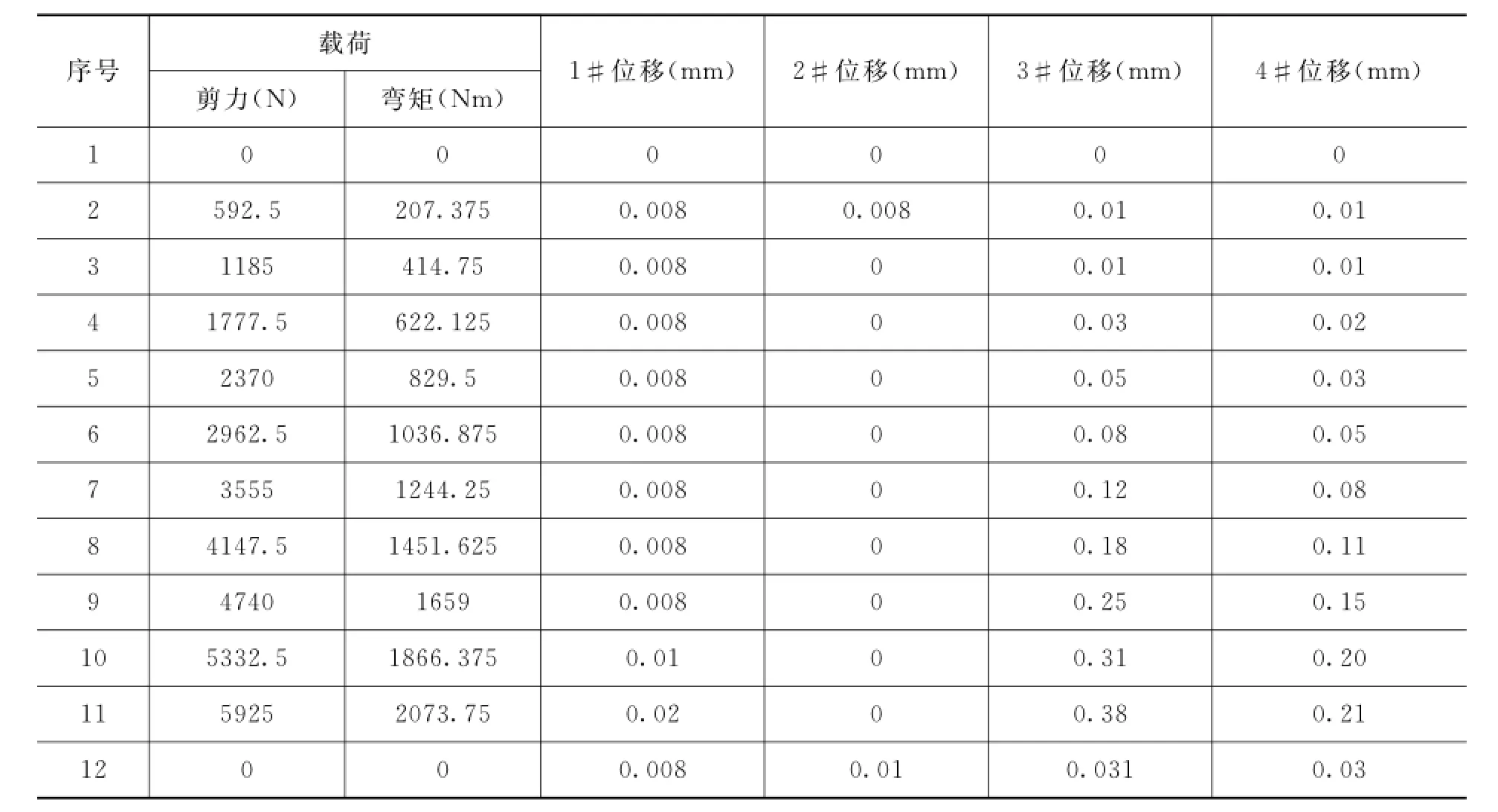
表2 舱体静力试验位移测量数据

从表2数据分析,在最大过载情况下,壳体位移值仅为0.38 mm,且在卸载后,位移值迅速恢复至0.031 mm,可见,在150%使用载荷作用下,壳体并未发生塑性变形,而是仍处在弹性变形阶段。

该试验结果有利的支撑了仿真试验的结果,从零件承受载荷和零件受力产生位移两方面同时验证了设计的合理性,为薄壁壳体类零件的设计提供了一条设计、仿真和实物试验的思路。

4 结束语

本文通过有限元仿真分析和实物试验建立了薄壁壳体类零件设计的思路,完善了薄壁壳体零件的设计与分析。

［1］程燕平.静力学［M］.哈尔滨：哈尔滨工业大学出版社,1999.

［2］张少实.新编材料力学［M］.北京：机械工业出版社,2002.

［3］张国瑞.有限单元法［M］.北京：机械工业出版社, 1992.

［4］王勋成,邵敏.有限单元法基本原理和数值方法［M］.北京：清华大学出版社,1995.

［5］ANSYS公司北京办事处.ANSYS入门手册［S］. 2003.

［6］R.D.库克,程耿东,等译.有限元分析的概念和应用［M］.北京：科学出版社,1989.

Statics Simulation and Statics Test of a Thin-walled Shell Part

LV Zhong-wei, GU Feng, DAI Xiu-fen
（Shanghai Radio Equipment Research Institute,Shanghai 200090,China）

The statics analysis of thin-walled shell was performed via finite element.The design and statics analysis methodology of spareparts made from thin-walled shell was established according to the simulation test result.

shell；statics simulation；statics test

TJ43

A

1671-0576（2014）01-0018-03

2013-03-26

吕忠卫（1981-）,男,硕士,高级工程师,主要从事引信结构设计研究。