一种相参Radon变换的高速微弱目标检测方法

刘俊豪, 陈 潜, 陆满君

（上海无线电设备研究所,上海 200090）

一种相参Radon变换的高速微弱目标检测方法

刘俊豪, 陈 潜, 陆满君

（上海无线电设备研究所,上海 200090）

针对高速微弱目标回波信号,进行长时间相参积累时出现的跨距离单元走动问题,文章采用基于图像旋转的方法实现相参Radon变换,并提出将信号空间变换到极距-多普勒域进行峰值检测。通过理论分析和数值仿真结果表明,该方法具有较高的积累增益和检测性能,能有效地避免多普勒模糊的影响。

高速目标；距离走动；相参变换；目标检测

0 引言

隐身技术和高性能武器装备的发展,对传统雷达构成严重的威胁,而长时间相参积累技术能有效的对隐身等微弱目标进行检测［1-3］。但在雷达信号长时间相参积累处理中,目标高速运动引起的跨距离走动严重影响目标能量的积累和检测［2,3］。

目前,对跨距离单元走动的补偿主要有距离门拉伸［4］、时域或频域插值移位补偿［5］、Keystone变换等［6］。距离门拉伸法对距离分辨率要求不高,且在处理过程中将不同距离门的噪声“拉”了进来,造成信噪比恶化；插值移位类方法是基于搜索的方法,运算量大,且有插值损失；Keystone变换方法需要对多普勒模糊数进行专门补偿,难以实现对不同模糊数目标的同时相参积累。

Radon变换是一种非相参积累的方法,在“检测前跟踪（TBD）”技术中实现对微弱目标的检测［7］,但其存在SNR阈值现象,对低SNR积累效率不高。最新的研究成果中,文献［2］提出的Radon-Fourier变换算法是基于时域移位和寻址运算的方法,需要对起始距离和速度进行联合搜索；文献［8］提出的构造耦合项相位因子方法同样是基于速度搜索的策略,同时需要对速度模糊数进行搜索；文献［9］提出相参Radon变换对微弱目标的检测,其在极距-角度域进行检测,且没有详细的分析过程。

本文采用图像旋转的思路,对相参Radon变换进行分析给出信号处理过程,提出在新的变换空间进行峰值检测,并进行性能分析。

1 目标回波信号模型

假设雷达发射Chirp信号,对于单点目标回波信号一个相参积累间隔（CPI）内雷达接收到的第m个回波基带信号为

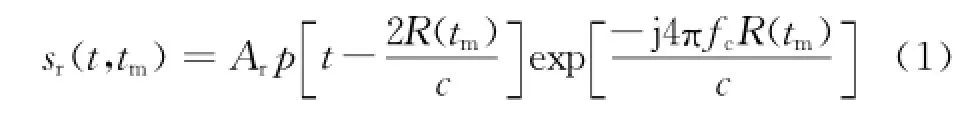
式中：t和tm分别为快时间和慢时间［tm=m T,且T为脉冲重复间隔（PRI）］；fc为载波频率；c为光速；Ar为点目标的回波幅度；R（tm）=R0+υtm,其中R0和R（tm）分别为t0和tm时刻目标相对于雷达的径向距离；p（t）=rect（t/Tp）exp（jπγt2）为发射的Chirp信号。

式（1）的频域形式：

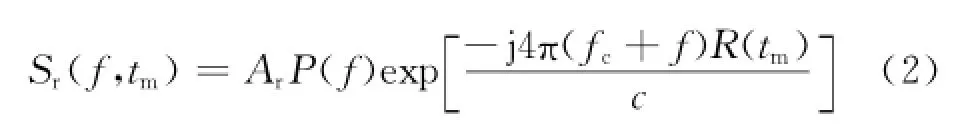
式中：P（f）为p（t）的频域表示。

上式在距离频域乘以P*（f）进行匹配压缩,得

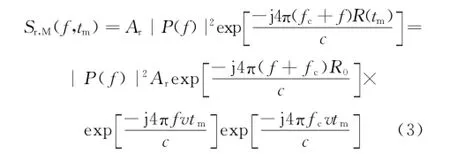
式中：exp（-j4πfυtm/c）为距离和速度耦合项,引起包络随慢时间走动。

将式（3）转化为时域形式：

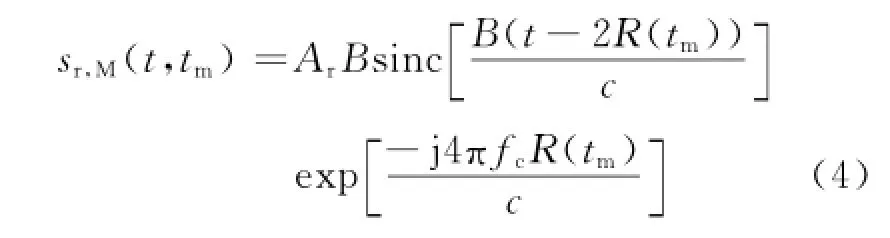
从上式可知,基带回波通过脉冲压缩后其包络为sinc函数,其中心频率在2R（tm）/c处。因此,不同的脉冲对应的中心频率不同,当在相参积累时间内相对运动超过一个距离分辨率单元时,即发生了跨距离门走动。

2 相参Radon变换原理及实现过程

2.1 Radon变换原理

Radon变换基本思想是对某个多元函数在给定的路径上进行积分运算,将Radon变换用于信号检测是一种非相参积累方法。

在一个平面内沿某一曲线对g（x,y）做线积分,得到的像就是函数g的Radon变换。设二维平面（x,y）有一任意二维函数g（x,y）,则Radon变换可以写成

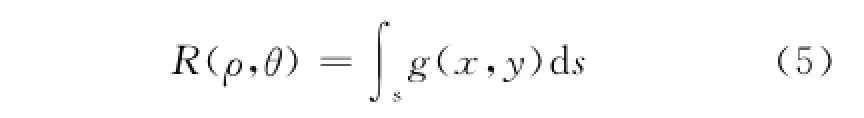
式中：s表示积分方向；θ为坐标轴围绕原心旋转的角度；ρ为原点到积分直线的距离。上式表明,线性Radon变换是对每一个旋转角度进行投影累加,如图1的虚线部分。

由三角关系知,平面（x-y）和平面（ρ-s）的关系为

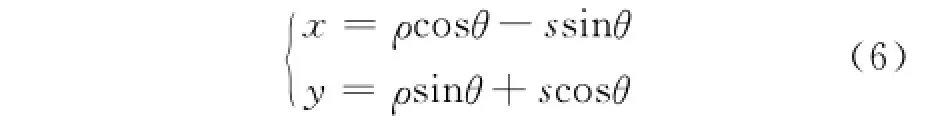
将上式代入式（5）,于是Radon变换为

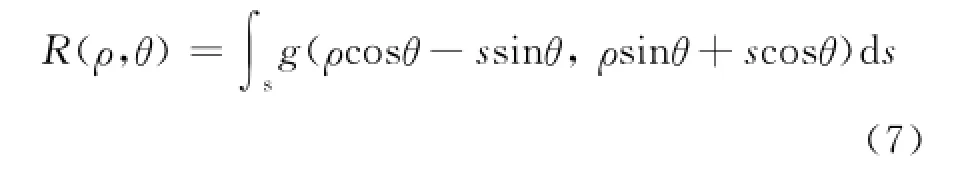
采用Radon变换将距离-脉冲域（r-tm域）信号空间变换到Radon参数空间（ρ-θ）,把信号空间看作图像来处理,对于匀速运动模型采用Radon变换是对目标的运动轨迹进行寻找,而参数空间的峰值位置对应目标轨迹的截距和斜率。

因此,Radon变换的处理过程：把信号空间r-tm域目标包络轨迹看作图像,首先利用信号空间到参数空间的旋转关系对图像进行旋转；由于旋转θi后,新的位置坐标可能不为整数,而像素值只在坐标整数处有定义,可对旋转的图像坐标进行插值,通常采用双线性内插；旋转后沿垂直方向累加,得到一个旋转角度θi对应的累加值；遍历搜索角度得到（ρ-θ）参数空间,过程如图1所示。最后,在（ρ-θ）空间通过检测峰值确定目标是否存在,并给出峰值对应的目标距离和速度。

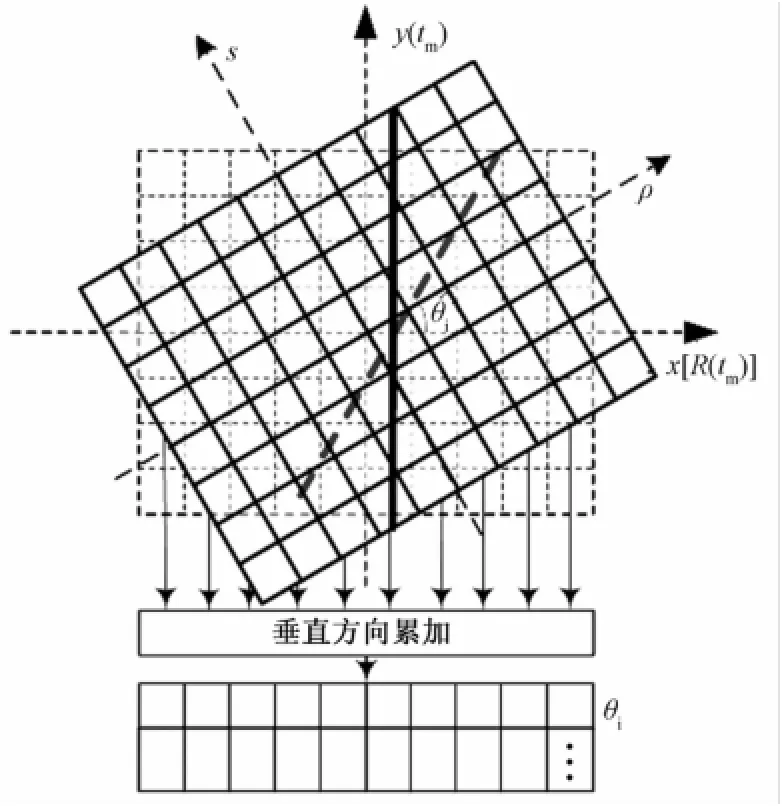
图1 Radon变换信号处理流程

2.2 相参Radon变换算法

在运用Radon变换对信号轨迹进行检测过程中,旋转后直接幅度累加得到积累结果,这样没有充分利用回波信号的相位信息。对信号空间进行旋转过程中,旋转角度与目标相对速度对应,因此每一个角度都有一个相对应的中心多普勒频率。利用该多普勒频率对旋转之后的信号空间进行相位补偿再累加,即利用Radon变换实现相参积累,该过程称为相参Radon变换。

将式（4）表示的信号空间sr,M（t,tm）看作图像,将其角度旋转θ后补偿相位并累加。则相参Radon变换可以表示为

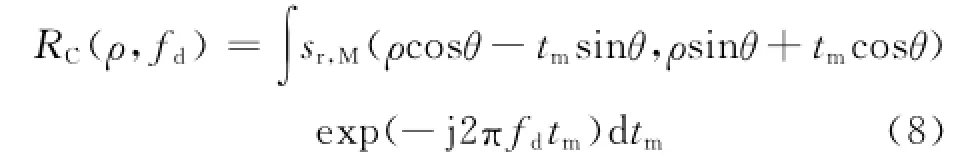
式中：Rc（ρ,fd）表示相参Radon变换积累结果；fd=-2υ/λ,且相对径向速度υ和角度θ的关系为

式中：T为脉冲重复间隔；ΔR为距离分辨率。

事实上,通过Radon变换将轨迹旋转,当轨迹沿垂直方向时,相位仍然随慢时间均匀变化,通过沿列方向FFT操作就可以得到相位校正和相参积累结果。此时得到的是一个旋转角度对应的极距-多普勒域（ρ-fd域）,对所有搜索角度得到的（ρ-fd）域的峰值进行选大处理,并通过恒虚警检测得到检测结果,该过程如图2所示。

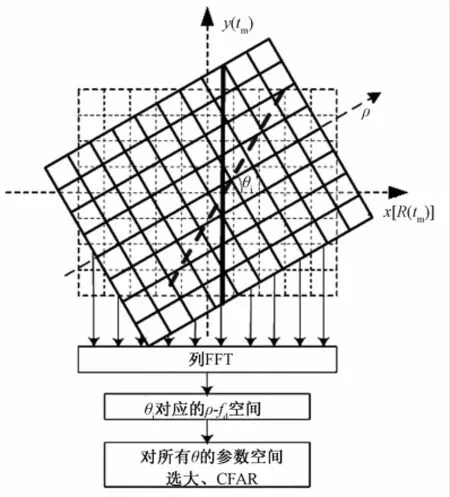
图2 相参Radon变换信号检测处理流程

在（ρ-fd）域进行峰值检测,类似于MTD的峰值检测,具有很好的抑制噪声能力［10］。

如果当信号空间角度旋转θi时,在ρ-fd空间得到最大的峰值,此时fd对应的速度在欠采样情况下存在速度折叠。但是θi对应原信号空间目标轨迹的斜率,故可由θi得到目标的相对速度式（9）,这样就避免了对模糊数的搜索。该过程的实现可以表示为

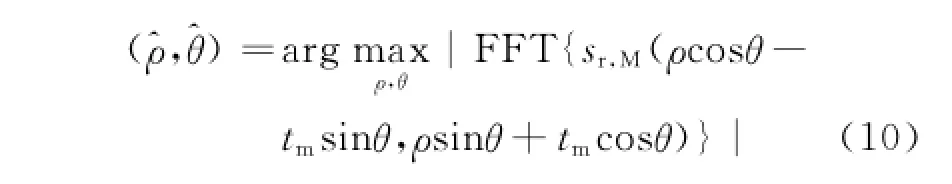
在旋转过程中角度的搜索步长太小会增加运算负荷,而步长太大会跨过最大峰值对应的角度。因此,在围绕信号空间中心进行旋转过程中,考虑旋转一个角度步长Δθ时,最远的点跨越一个距离单元以内,即

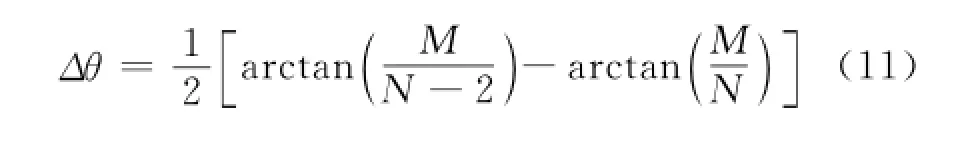
式中：N为距离门单元数；M为积累脉冲数；减去“2”是考虑围绕信号空间中心旋转,垂直方向取一半。

3 仿真与分析

设单点目标速度υ=2 000 m/s相向雷达运动,雷达波长3 cm,信号带宽B=10 M Hz,时宽Tp=20μs,采样频率fs=10 M Hz,重频fr= 2 k Hz,相参积累脉冲数M=1 024,距离维单元数M=256。则相参积累时间0.512 s,距离分辨率ΔR=15 m,跨距离单元数为68,因此对应的轨迹斜率为3.80°,设置角度搜索范围为-5°～5°。图像围绕中心进行旋转,由式（11）得到步进为0.112°,故这里取Δθ=0.1°进行搜索,并且仿真过程中加入SNR为-20 dB的高斯白噪声。

在长时间积累过程中高速目标位置引起的跨距离单元走动如图3所示,由于存在严重的距离走动现象,直接将其FFT处理进行相参积累,结果如图4和图5所示。图中可以看出：MTD结果积累幅度不高,检测性能差；而用Radon变换寻找目标轨迹信息,结果如图6所示,可以看出存在积累峰值,但很明显非相参的影响使得噪声平面抬高,造成积累效率不高。

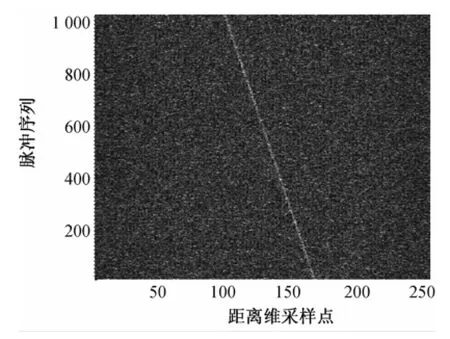
图3 目标包络轨迹

采用本文方法,通过角度搜索对信号空间坐标进行旋转,然后双线性插值,仿真中插值模板为2×2。当包络沿慢时间维对齐时的包络如图7所示。将其作FFT操作得到相参积累结果,如图8所示,得到ρ-fd平面的目标峰值远远高于噪声。

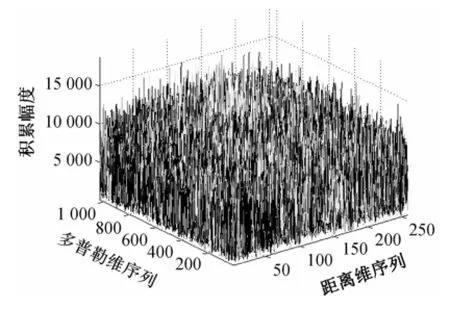
图4 MTD的积累结果

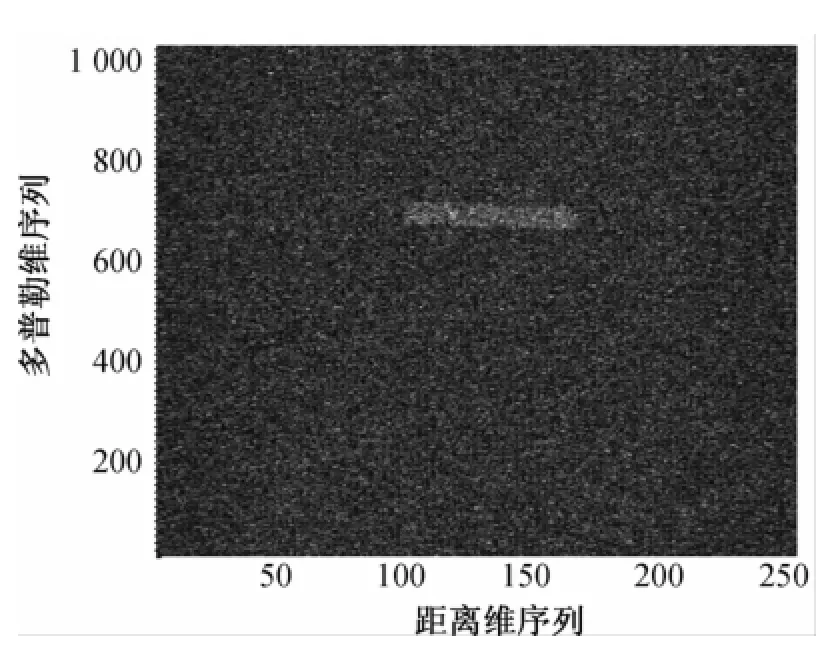
图5 MTD结果俯视图

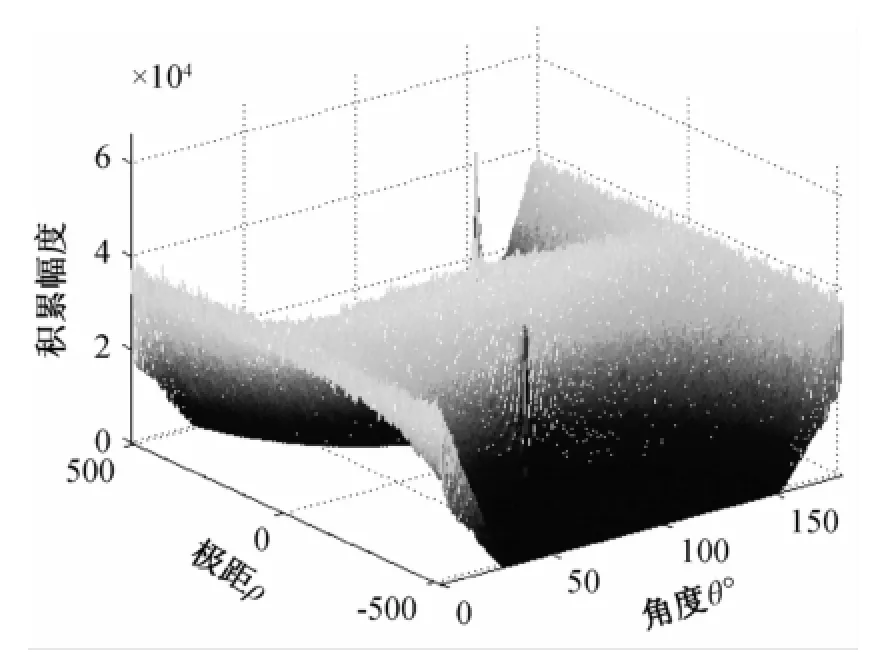
图6 Radon变换结果

根据上面仿真数据,对不同输入SNR进行1 000次Monte Carlo实验,实验结果如图9所示。仿真中MTD方法的脉冲积累个数刚好跨一个距离单元,在图5中包络跨越68个距离单元（18.32 d B）,积累能量分散在这些单元内。从图中可以看出,在虚警率为10-6,检测概率为0.9时,采用本文的相参Radon变换方法最小可检测SNR为-32 dB,比MTD方法低15.8 dB,接近理论值18.32 dB,这是由于双线性插值引起的插值损失,并且比Radon变换低8.2 dB,显著提高了检测性能。

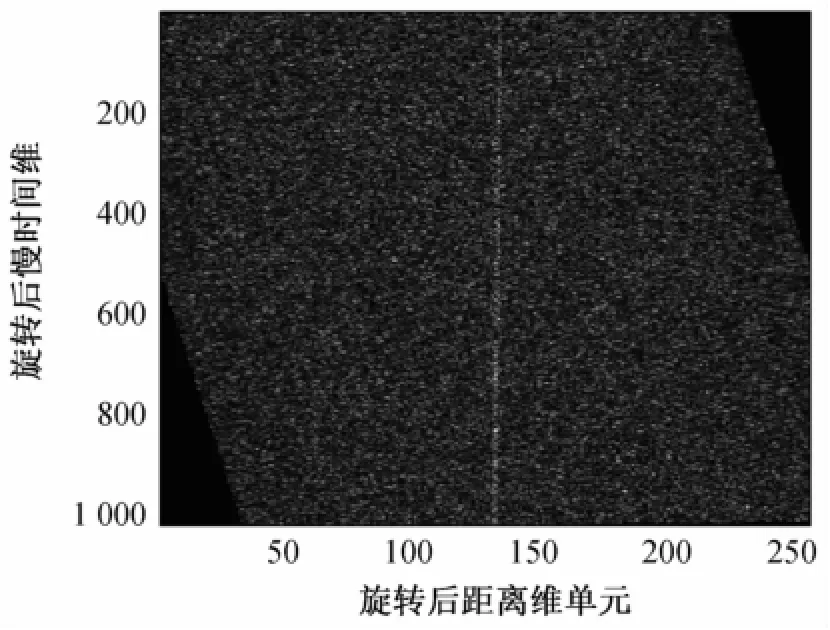
图7 信号空间旋转对齐时的包络

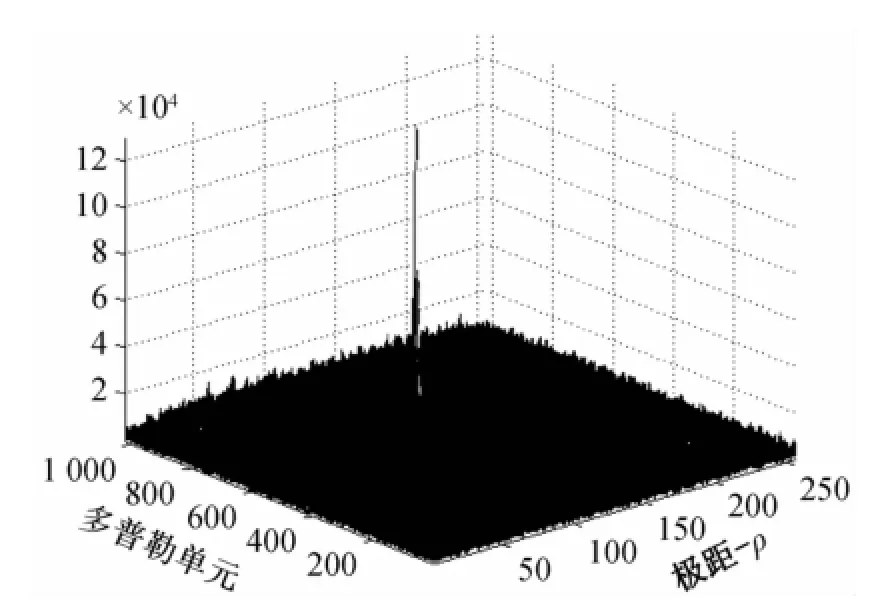
图8 相参Radon变换积累结果（ρ-fd）域

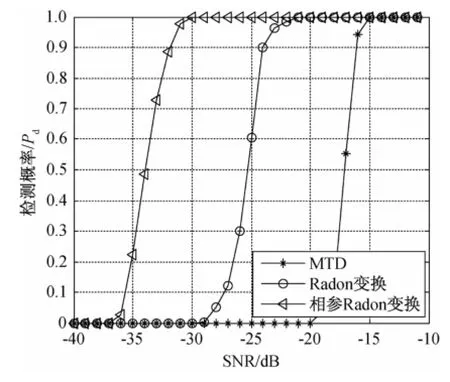
图9 虚警概率为10-6时目标的检测概率

4 结束语

本文在Radon变换的基础上,采用基于图像旋转的方法实现相参Radon变换,并提出在参数空间极距-多普勒域进行峰值检测,得到目标的运动轨迹。从得到最大峰值对应的角度得到目标的速度,避免了欠采样时多普勒模糊的影响。

通过数值仿真表明,该算法具有良好的抑制噪声的能力,并且具有很高的积累增益和较好的检测性能。

［1］保铮.雷达信号的长时间积累［C］.第七届中国雷达学术年会论文集.南京：中国电子学会,1999.

［2］Xu J,Yu J,Peng Y,et al..Radon-Fourier Transform for Radar Target Detection I：Generalized Doppler Filter Bank［J］.IEEE Transactions on Aerospace and Electronic Systems,2011,47（2）：1183-1202.

［3］曾建奎,何子述,刘红明.一种基于改进Hough变换的雷达检测方法［J］.电波科学学报,2008,23（5）：838-840,904.

［4］王俊.微弱目标信号积累检测的包络移动补偿方法［J］.电子学报,2000,28（12）：56-59.

［5］陈远征,朱永峰,等.基于包络插值移位补偿的高速运动目标的积累检测算法研究［J］.信号处理, 2004,20（4）：387-390.

［6］张顺生,曾涛.基于Keystone变换的微弱目标检测［J］.电子学报,2005,33（6）：1675-1678.

［7］Carretero Moya,J.Application of the Radon Transform to Detect Small Targets in Sea Clutter［J］.Radar Sonar&Navigation,2009,3（2）：155-166.

［8］战立晓,等.一种新的超声速弱目标长时间相参积累算法［J］.现代雷达,2013,35（5）：47-51.

［9］Javier C M,Javier G M,et al.A Coherent Radon Transform for Small Target Detection［C］.IEEE Rader Conference,2009：1-4.

［10］Richards M A（著）.邢孟道,王彤,李真芳,等（译）.雷达信号处理基础［M］.北京：电子工业出版社,2010：187-200.

A Coherent Radon Transform for High-speed and Weak Target Detection Method

LIU Jun-hao, CHEN Qian, LU Man-jun
（Shanghai Radio Equipment Research Institute,Shanghai 200090,China）

Focusing on the across range unit migration during the long-term coherent integration period for high-speed and weak target,echo signal the coherent Radon transform based on image rotation is implemented in this paper,and a novel peak detection method is proposed in Pole Distance-Doppler Domain transformed from Signal Domain.The theoretical analysis and numerical results show that a higher coherent integration gain and better detection performance and the Doppler ambiguity can also be avoided efficiently.

high-speed target；range walk；coherent transform；target detection

TN957

A

1671-0576（2014）01-0036-05

2013-09-28

刘俊豪（1988-）,男,在读研究生,主要从事雷达信号处理技术的研究。