基于Friedman检验的非参数协作频谱感知方法

王炯滔 金 明 李有明 高 洋



基于Friedman检验的非参数协作频谱感知方法

王炯滔①②金 明*①②李有明①高 洋②

①(宁波大学信息科学与工程学院 宁波 315211)②(西安电子科技大学综合业务网理论及关键技术国家重点实验室 西安 710071)

协方差矩阵频谱感知方法在天线相关性低时感知性能较差，该文针对这一问题提出一种基于Friedman检验的非参数协作频谱感知方法。分布式放置的感知节点具有空间分集的特性，因此在同一时刻感知节点上的信号功率不完全相同。利用这一特点，提出通过比较各感知节点的信号功率水平来实现频谱感知。由于采用了非参数化表示，该方法对噪声不确定性稳定，且适用于任意统计分布的噪声。另外，推导了所提方法判决门限的理论表达式，结果显示判决门限与采样点数无关，因此在采样点数变化的情况下无需重新设置判决门限。仿真结果验证了上述理论分析的有效性。

认知无线电；协作频谱感知；Friedman检验；非参数

1 引言

宽带高速率的无线通信业务需要大量频谱资源的支撑，有限的可用频谱资源以及低效的静态频谱分配政策使得频谱资源缺乏的现象越来越严重[1]。一方面，无线通信业务的快速发展和各种系统、协议、网络的不断出现，使更多的无线业务竞争无线频谱资源；另一方面，大部分可用频段已经分配给了授权用户，非授权用户只能使用那些不需要授权的频段，而非授权频段已趋于饱和。目前频谱管理中广泛采用静态频谱分配方式，此分配方式的排外特性使得大量空闲频谱得不到使用，进而导致频谱利用率非常低，从而成为造成频谱资源短缺现象的主要原因之一。为解决这一问题，频谱管理者开始考虑用动态频谱分配方式来进行频谱管理[2]。

认知无线电(Cognitive Radio, CR)技术能够有效提高频谱资源利用率，是实现频谱资源动态分配的主要方案之一[3,4]。频谱感知是认知无线电技术的重要组成部分，可以有效防止采用认知无线电技术的无线通信业务对在同一频段中其它无线通信业务产生干扰，故频谱感知的性能直接关系到无线通信业务的质量。

传统的认知无线电频谱感知方法有能量检测(Energy Detection, ED)法[5,6]，匹配滤波器法[7,8]和循环平稳检测法[9]等。其中，ED法实现简单，但要求噪声功率已知，而在实际中噪声功率无法有效获得，噪声不确定性会使ED法的感知性能急剧下降；匹配滤波器法在高斯白噪声环境下可以使信噪比最大化，同时达到较高的处理增益所需的时间比较少，但其需要知道授权用户信号波形的先验知识，当先验知识不准确时，该检测算法的性能会受到较大影响；循环平稳检测法在授权用户发射信号功率谱密度较低时，也能有效地检测频谱空穴，但其需要信号循环特征频率的先验知识，而在实际中可能无法预先获得信号循环特征频率，此外该方法计算量较大。

近几年有人提出利用感知节点相关性来克服噪声不确定性的频谱感知方法。这些检测方法主要分为两类：特征值检测[10,11]和协方差检测[12,13]。特征值检测主要包括最大最小特征值法(Maximum- Minimum Eigenvalue Detection, MMED)和最大特征值检测法(Maximum Eigenvalue Detection, MED)。它们利用采样信号协方差矩阵的特征值来实现频谱感知。然而在频谱感知过程中，特征值的求解往往需要较大的计算量，因而此类方法的计算复杂度较高。基于协方差矩阵的频谱感知方法主要有协方差绝对值(Covariance Absolute Value, CAV)法和协方差范数(Covariance Frobenius Norm, CFN)法。它们是在感知节点之间信号具有相关性而噪声不具有的假设下，通过比较采样所得信号和噪声的协方差矩阵中的非对角元素来实现频谱感知，这两种方法具有相同的感知性能。协方差检测虽然有较低的复杂度，也不需要知道噪声的先验信息，但当假设不成立时，即感知节点之间信号相关性较低或噪声有相关性时，感知性能会大大下降，甚至不能进行频谱感知。

针对ED法对噪声不确定性敏感和CAV法在感知节点之间信号相关性差或存在色噪声时感知性能下降的问题，本文提出一种基于Friedman检验[14]的非参数协作频谱感知方法。Friedman检验是一种非参数化检验，该算法不需要知道噪声和信号的先验信息，感知性能不受噪声不确定性和感知节点相关性等的影响。对于给定的恒虚警概率，如果采样点数发生变化，已有的频谱感知方法需要重新计算判决门限以满足恒虚警要求。而本文所提方法中，判决门限只与恒虚警概率有关，与采样点数无关；也就是说，当采样点数变化时，不需要重新计算判决门限。另外，本文方法的虚警概率不会随采样点数的改变而改变，而其检测概率会随着采样点数的增加而提高。

2 信号模型

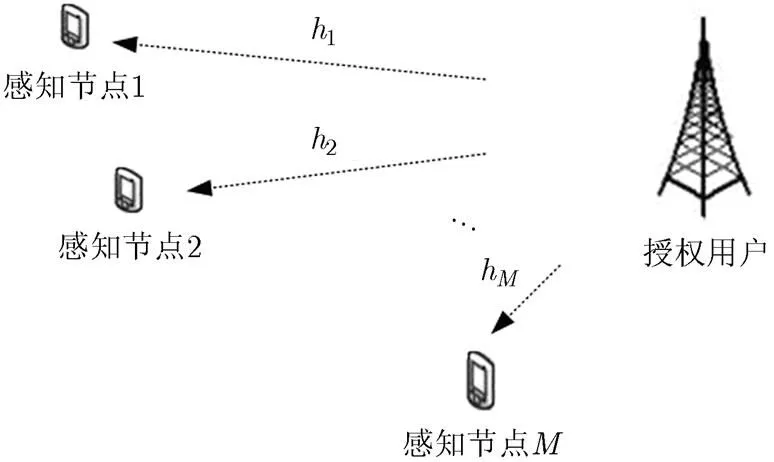
图1 认知无线电系统模型

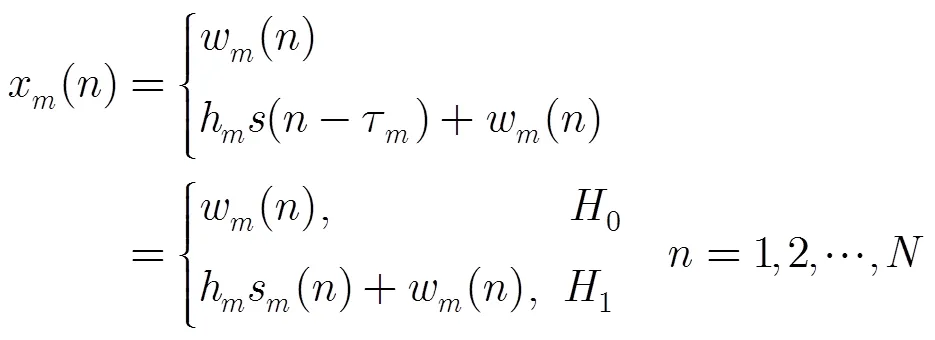
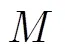
求得各感知节点采样信号的瞬时功率矩阵为

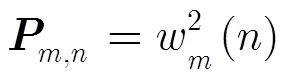
而当存在授权用户时，则可以表示为

2000国家大地坐标系(CGCS2000，China Geodetic Coordinate System 2000)是中国自主建立、适应现代空间技术发展趋势的地心坐标系。按照国务院推广使用2000国家大地坐标系的要求，明确于2018年6月底前全面完成国土资源空间数据向2000国家大地坐标系转换工作，并使用2000国家大地坐标系[1-2]。原有的国土资源空间数据大多采用1980西安坐标系、1954年北京坐标系或其它地方坐标系，为保证国土资源大数据的统一管理，促进全国自然资源大数据信息化工作的顺利开展，全国很多县市都陆续开展了国土资源空间数据2000国家大地坐标系转换工作。

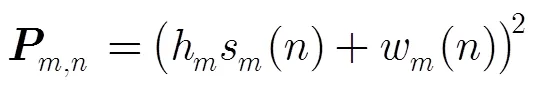
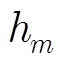
3 非参数协作频谱感知及判决门限

Friedman检验是一种实现多个总体分布是否存在显著差异的非参数检验方法[14]，因此可以用来检测感知节点上的功率水平是否一致。受Friedman检验的启发，本文提出基于Friedman检验的非参数协作频谱感知方法。由于采用了非参数化的手段，该方法对噪声不确定性稳健，且对噪声的统计分布没有要求。

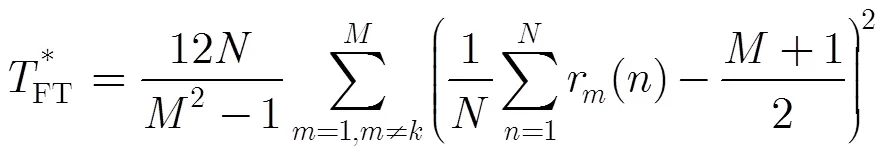
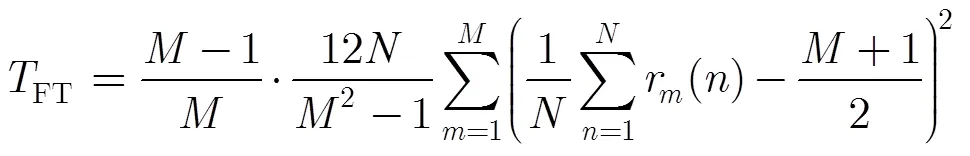
判决门限的设置会影响虚警概率，为了使系统满足预定的恒虚警概率，判决门限的计算非常重要。如果采用通过数值仿真来设置判决门限的方法，当系统参数变化(如感知节点数量改变)后，就需要重新仿真来设置判决门限，从而严重增加系统的计算负担。为此，本文分析得到了判决门限的理论表达式。

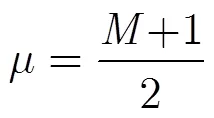
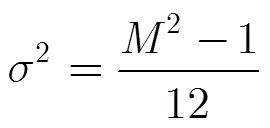
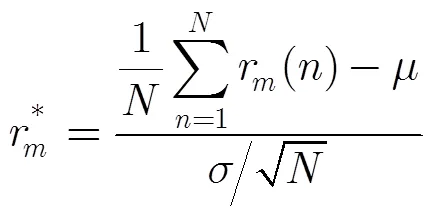
服从标准正态分布，即

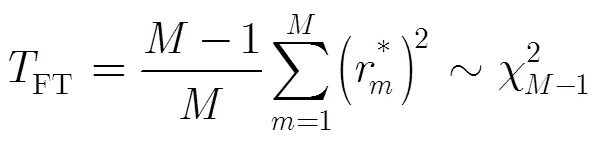
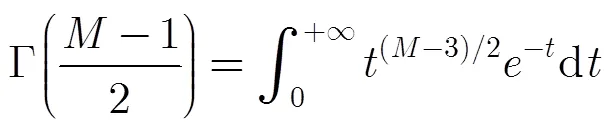
由式(16)可知，在不存在授权用户情况下，检验统计量的分布与采样点数无关。这个特点使得该方法的判决门限只与感知节点数目和恒虚警概率有关，而与采样点数无关。也就是说，如果保持判决门限不变，虚警概率不会随采样点数的改变而改变。另外，仿真结果表明，该感知方法的检测概率会随采样点数的增加而提高。

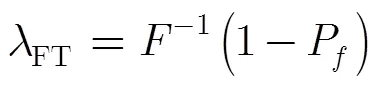
4 仿真分析

本节通过数值仿真比较所提方法与ED法及CAV法的频谱感知性能。实验1到实验4中假设为高斯白噪声信道，实验5中假设为色噪声信道。所有实验中假设感知节点数目为4，预设的虚警概率为0.1。

实验2 本实验研究判决门限不变的情况下，检测概率是否会随着采样点数的增加而提高。首先在虚警概率为0.1，采样点数为500点的参数下设定3种感知方法的判决门限；然后改变接收信号采样点数，同时利用这些设定好的判决门限进行频谱感知。仿真中假设信噪比为-10 dB，仿真得到以上3种方法的虚警概率和检测概率分别如图3和图4所示。

比较图3和图4可知，对于给定的判决门限，CAV法的虚警概率和检测概率会随着采样点数的增加而下降，ED法的虚警概率和检测概率会随着采样点数的增加而增加。这说明当设置门限时的采样点数与实际的信号采样点数不同时，ED法和CAV法获得的虚警概率会偏离预先设定的虚警概率，使得其检测概率不是在恒虚警情况下得到。由于本文方法的判决门限与采样点数无关，所以不管采样点数是多少，都能获得恒定的虚警概率(如图3所示)。图4中本文方法的检测概率曲线表明，尽管其虚警概率与采样点数无关，但其检测概率却会随着采样点数的增加而增加。

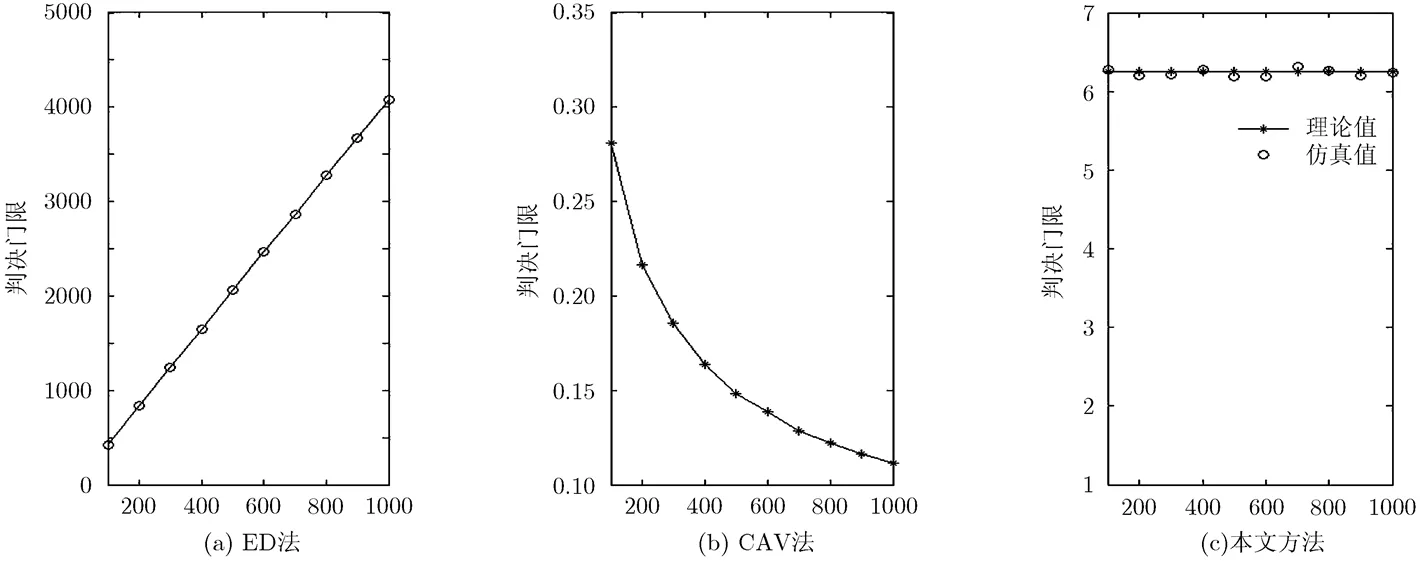
图2 恒虚警概率时，判决门限随信号采样点数的变化

实验3 本实验在感知节点上信号之间相关系数变化时，比较研究本文方法与CAV法的性能(ED法与感知节点相关系数无关，所以本实验不作研究)。仿真过程中信号采样点数为500，相关系数分别选0.9和0.3，两种方法的检测概率随信噪比变化如图5所示。图5表明当感知节点相关系数下降时，CAV法频谱感知性能会明显下降，但本文方法感知性能与节点相关系数无关，依然保持较好的感知性能。

实验4 本实验研究噪声不确定性对感知性能的影响。由于CAV法不需要噪声功率的先验知识，所以本实验只比较ED法和本文方法。仿真条件与实验3相同。对于噪声不确定性为0.5 dB和1.0 dB情况，检测概率如图6所示。图6表明当噪声不确定性增加时，ED法的频谱感知性能会大大下降。由于所提方法不需要噪声功率的先验知识，所以该方法对噪声不确定性稳健。

实验5 分析色噪声对本文方法检测性能的影响。假设背景噪声为色噪声时相邻两个节点的噪声相关系数为0.5，仿真得到色噪声情况下与高斯白噪声情况下的检测概率与虚警概率如图7和图8所示。

图7和图8表明当存在色噪声背景时，由于色噪声的相关性使得CAV法的检测概率和虚警概率都大大增加，而本文方法不受噪声相关性的影响，依然保持良好的感知性能。

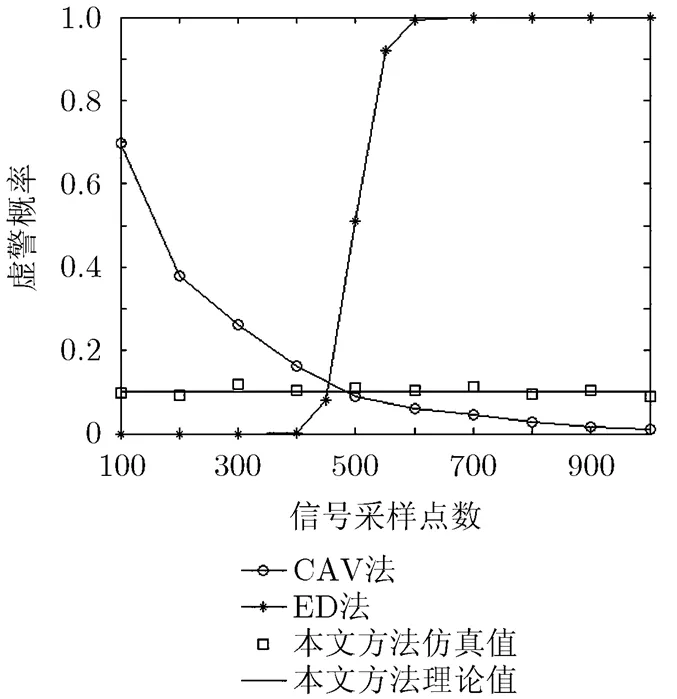
图3 不同采样点数下虚警概率比较

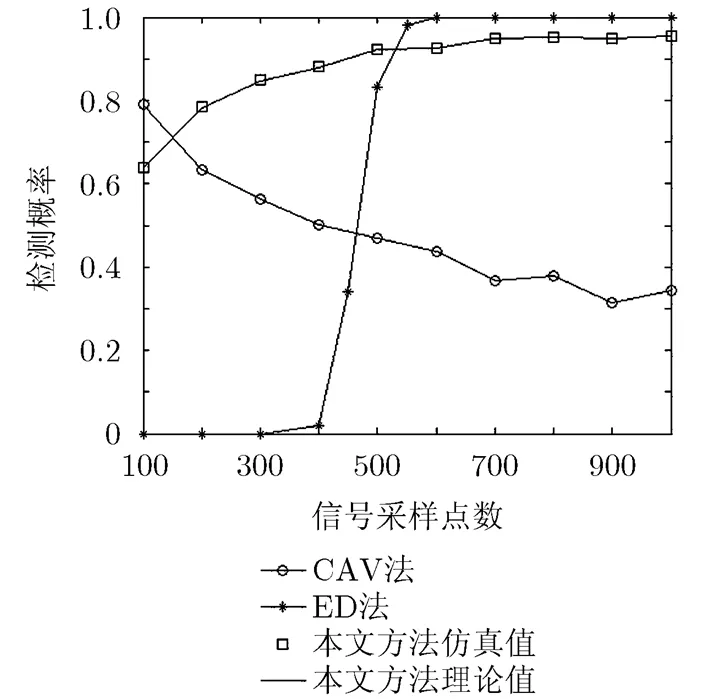
图4 不同采样点数下检测概率比较

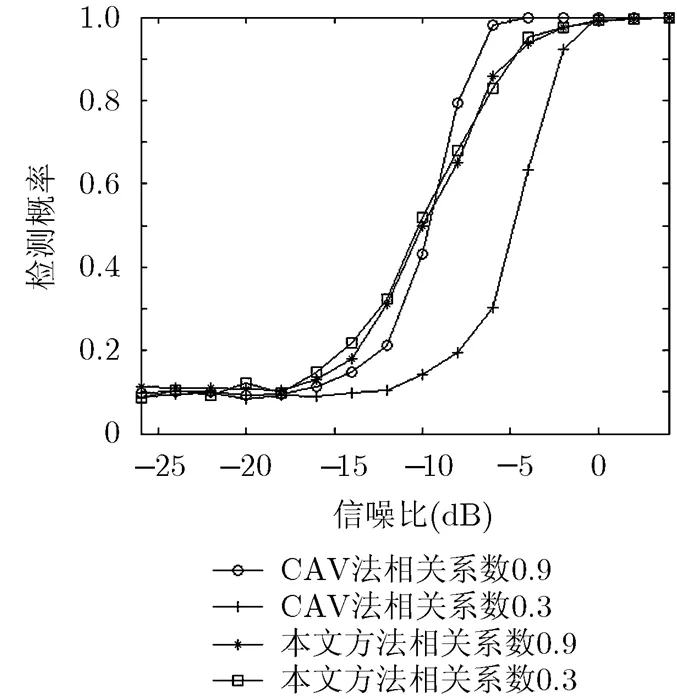
图 5 不同相关系数下检测概率比较

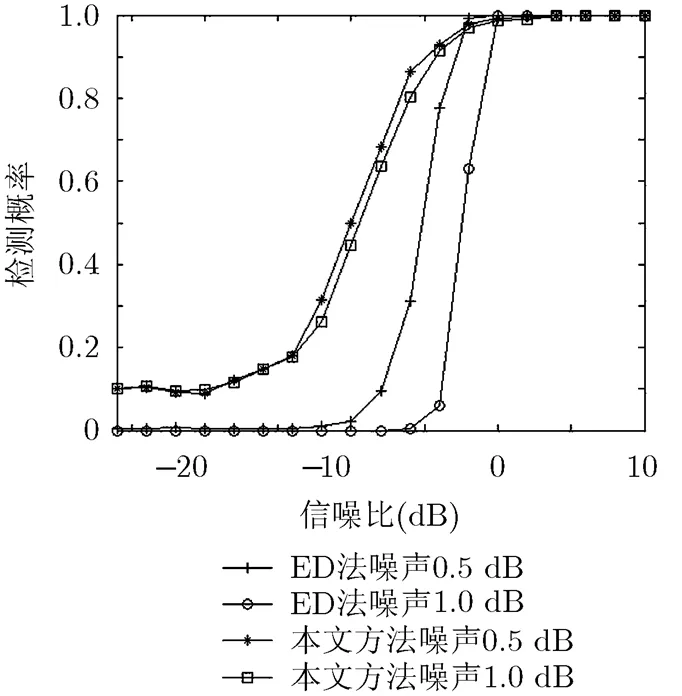
图6 不同噪声不确定性下检测概率比较

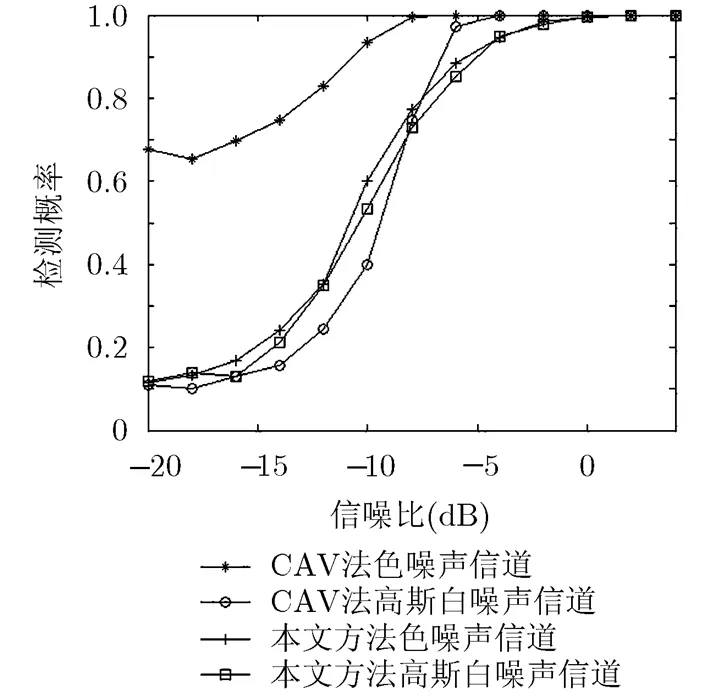
图7检测概率比较

图8虚警概率比较

5 结论

本文提出了一种基于Friedman检验的非参数协作频谱感知方法，其判决门限与采样点数无关，且对噪声不确定性稳健。该方法不仅克服了能量检测法要求预知噪声功率先验知识的问题，而且克服了协方差绝对值法在感知节点相关性较低或存在色噪声时频谱感知性能下降的缺点。仿真结果表明，所提方法具有较高的检测性能。

[1] Mitola J, III Gerald Q and Maguire J R. Cognitive radio: making software radios more personal[J]., 1999, 6(4): 13-18.

[2] Garhwal A and Bhattacharya P P. A survey on dynamic spectrum access techniques for cognitive radio[J]., 2011, 3(4): 15-32.

[3] Elena G. Past, present and future of spectrum sensing in cognitive radio networks[J]., 2012, 5(2): 93-102.

[4] Koroupi F, Talebi S, and Salehinejad H. Cognitive radio networks spectrum allocation: an ACS perspective[J]., 2012, 19(3): 767-773.

[5] Kim S, Lee J, Wang H,..Sensing performance of energy detector with correlated multiple antennas[J]., 2009, 16(8): 671-674.

[6] Gismalla E H and Alsusa E. On the performance of energy detection using Bartlett's estimate for spectrum sensing in cognitive radio systems[J]., 2012, 60(7): 3394-3404.

[7] Chen H S, Gao W, and Daut D G. Signature based spectrum sensing algorithms for IEEE 802.22 WRAN[C]. IEEE International Conference on Communications, 2007, Glasgow, UK, 2007: 6487-6492.

[8] Cabric D, Tkachenko A, and Brodersen R W. Spectrum sensing measurements of pilot, energy, and collaborative detection[C]. 2006 IEEE Military Communications Conference, Washington, DC, 2006: 1-70.

[9] Sutton P D, Nolan K E, and Doyle L E. Cyclostationary signatures in practical cognitive radio applications[J]., 2008, 26(1): 13-24.

[10] Yang Miao, An Jian-ping, Bu Xiang-yuan,.. An improved eigenvalue-based algorithm for cooperative spectrum sensing[C]. The 6th International Conference on Wireless Communications Networking and Mobile Computing (WiCOM), Chengdu, 2010: 1-4.

[11] Nadler B, Penna F, and Garello R. Performance of eigenvalue-based signal detectors with known and unknown noise level[C]. 2011 IEEE International Conference on Communications (ICC), Kyoto, 2011: 1-5.

[12] Zeng Yong-hong and Liang Ying-chang. Spectrum-sensing algorithms for cognitive radio based on statistical covariances[J]., 2009, 58(4): 1804-1815.

[13] Jin Ming, Li You-ming, and Ryu Heung-gyoon. On the performance of covariance based spectrum sensing for cognitive radio[J]., 2012, 60(7): 3670-3682.

[14] Friedman M. The use of ranks to avoid the assumption of normality implicit in the analysis of variance[J]., 1937, 32(200): 675-701.

[15] 李建东, 郭梯云, 邬国扬. 移动通信[M]. 西安: 西安电子科技大学出版社, 2006: 133-142.

Li Jian-dong, Guo Ti-yun, and Wu Guo-yang. Mobile Communication[M]. Xi’an: Xi’an University of Electronic Science and Technology Press, 2006: 133-142.

[16] Soong T T. Fundamentals of Probability and Statistics for Engineers[M]. Jhon Wiley & Sons Ltd, 2004: 119-154.

王炯滔： 男，1988年生，硕士生，研究方向为认知无线电.

金 明： 男，1981年生，讲师，研究方向为认知无线电、阵列信号处理.

李有明： 男，1963年生，教授，研究方向为下一代无线通信系统、资源分配.

Nonparametric Cooperative Spectrum Sensing Algorithm Based on Friedman Test

Wang Jiong-tao①②Jin Ming①②Li You-ming①Gao Yang②

①(,,315211,)②(,,710071,)

Covariance matrix based spectrum sensing encounters performance degradation when there the antenna correlation is low. To overcome this drawback, a nonparametric cooperative spectrum sensing algorithm based on Friedman test is proposed. Distributed sensors possess the effect of space diversity, so that the signal power among the sensors at the same time may not be completely equal. Based on this feature, the spectrum sensing is realized by comparing signal powers among the sensors. For the nonparametric approach is adopted, the proposed algorithm is robust to noise uncertainty and is suitable for noise of any statistical distribution. The theoretical expression of decision threshold is also derived, which shows that the decision threshold has no relationship with the sample number. As a result, the threshold does not need to be reset when the sample number changes. Simulation results demonstrate the effectiveness of the algorithm.

Cognitive radio; Cooperative spectrum sensing; Friedman test; Nonparametric

TN92

A

1009-5896(2014)01-0061-06

10.3724/SP.J.1146.2013.00461.

2013−04−07收到，2103-07-27改回

国家自然科学基金(61071119)，浙江省自然科学基金(Y1110657, Y1091155)，浙江省重点科技创新团队(2010R50009)，宁波市科技创新团队(2011B81002)和浙江省重中之重学科开放基金(XKXL1301)资助课题

金明 jinming@nbu.edu.cn