麦克斯韦方程反演的大范围收敛共轭斜量法
王 迎
麦克斯韦方程反演的大范围收敛共轭斜量法
王 迎
(黑龙江工业学院 机械工程系,黑龙江 鸡西 158100)
针对麦克斯韦方程中的电导率参数反演问题,构造一种具有大范围收敛的正则化共轭斜量反演算法,即将用于求解非线性问题大范围收敛的同伦法、求解大规模优化问题的共轭斜量法与求解不适定问题的Tikhonov正则化方法有机结合,得到解决麦克斯韦方程反演问题大范围收敛的数值方法,以求解电导率参数反演问题,解决了求解过程中局部陷入极小值的困惑. 实验结果表明此算法是有效的,可以应用于其他类型的参数识别问题.
麦克斯韦方程;反演;同伦法;共轭斜量法
随着科学技术日新月异的发展进步,数学物理反演问题愈来愈广泛地存在于生活生产的诸多领域,尤为突出的是麦克斯韦方程反演问题在石油方面、电学方面以及天然气勘探等方面彰显出巨大应用潜力[1]. 针对于麦克斯韦方程的反演问题,现今已经产生很多方法应用于求解此类反演问题,然而这些方法下的反演过程相当复杂,并且计算量大、耗时,从很大程度限制了麦克斯韦方程反演问题在多个领域的广泛应用. 多种情况下,对于这类反演问题可以利用牛顿迭代法来解决,而利用牛顿迭代法存在的第一个困难就是建立的目标函数在局部上会呈现极小化的变化趋势(即局部收敛性). 因此需要寻找一种能够有效克服目标函数局部收敛性并且能够快速检索到所需解决的麦克斯韦方程反演问题在其整个定义区间最优解(全局最优解)的方法. 作为代数拓扑学重要组成部分之一的同伦方法是一种近些年来广泛应用于求解非线性问题大范围收敛的数值方法.
另外,由于近几年最优化方法迅猛发展,愈来愈多学者把最优化方法与正则化方法相融合,创造出更加优越的求解反演问题的有效方法,如正则化的内点方法、正则化的Broyden方法、正则化的共轭斜量方法等. 值得一提的是,作为最优化方法最常用方法之一的共轭斜量法由于具有小存储需求、算法简便等优点,并且石油勘探、大气模拟、航天航空等领域特大规模优化问题常常利用共轭斜量法求解的[2]. 因而,共轭斜量法非常适用于多个科学领域大规模优化问题的数值求解. 因此,正则化共轭斜量法可以用来求解麦克斯韦方程反演问题稳定性数值解.
因此,本文的总体思路是将用于求解非线性问题大范围收敛的同伦方法与求解大规模优化问题的共轭斜量法有机结合,并引入求解不适定问题的Tikhonov正则化方法,最终给出解决麦克斯韦方程反演问题大范围收敛的数值方法,以求解电导率参数反演问题.
1 数学模型
1.1 连续数学模型
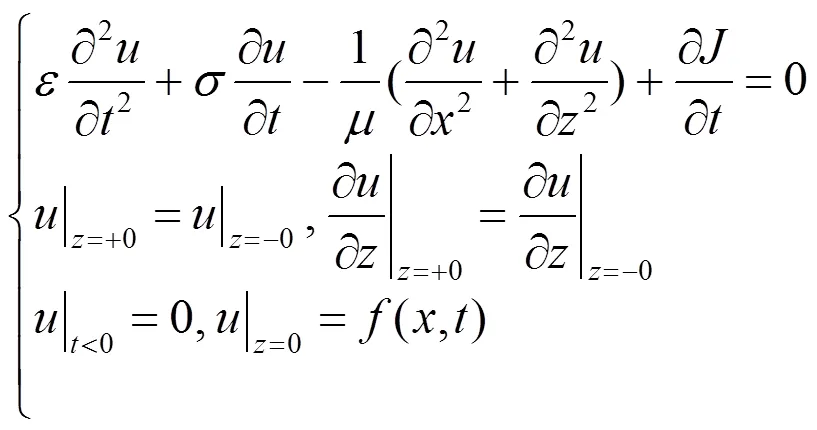
1.2 离散数学模型
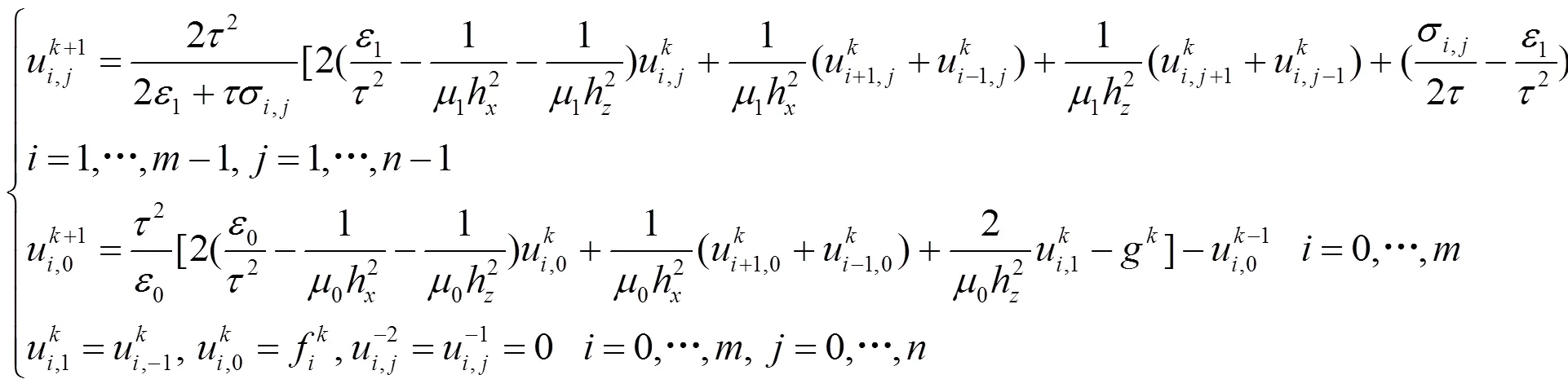
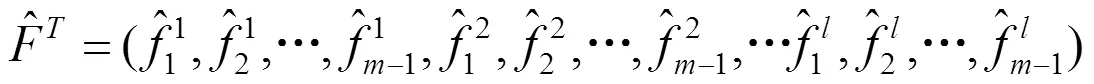
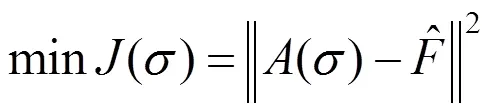
的非线性优化问题.
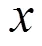
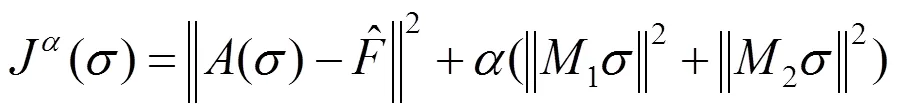
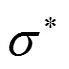
本文将把上式作为非线性反演的一般框架,在此框架下讨论麦克斯韦方程反演问题.
25层酒店客房低区生活水箱有2种作用,供水至酒店低区用水点兼酒店高区中途转输水箱。根据水规的要求:由水泵联动提升进水的水箱的生活用水调节容积,不宜小于最大用水时水量的50%,生活用水中途转输水箱的转输调节容积宜取转输水泵5~10min的流量等规定,该水箱容积需按酒店客房低区最大时用水量的50%和酒店高区水泵10min转输用水量之和确定。
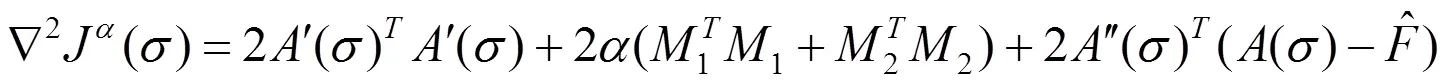
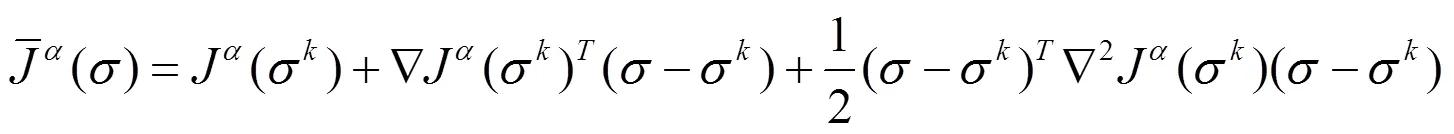
得到了这个二次逼近模型后,选取共轭斜量法来求解,其迭代式为
2 大范围收敛的共轭斜量方法的形成
应用同伦方法[5]获得梯度
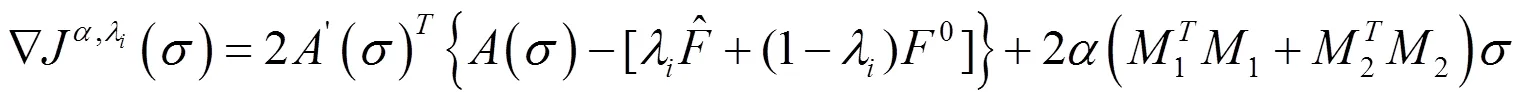
至此,形成大范围收敛的共轭斜量法,其流程如下所示:
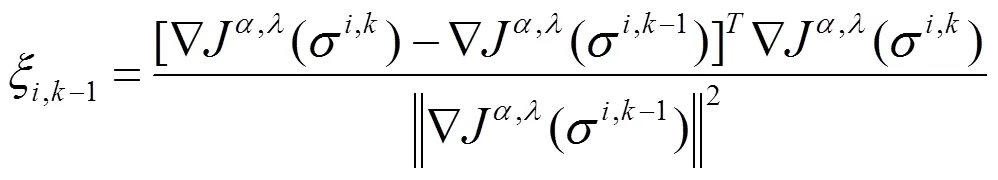
3 数值模拟
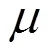
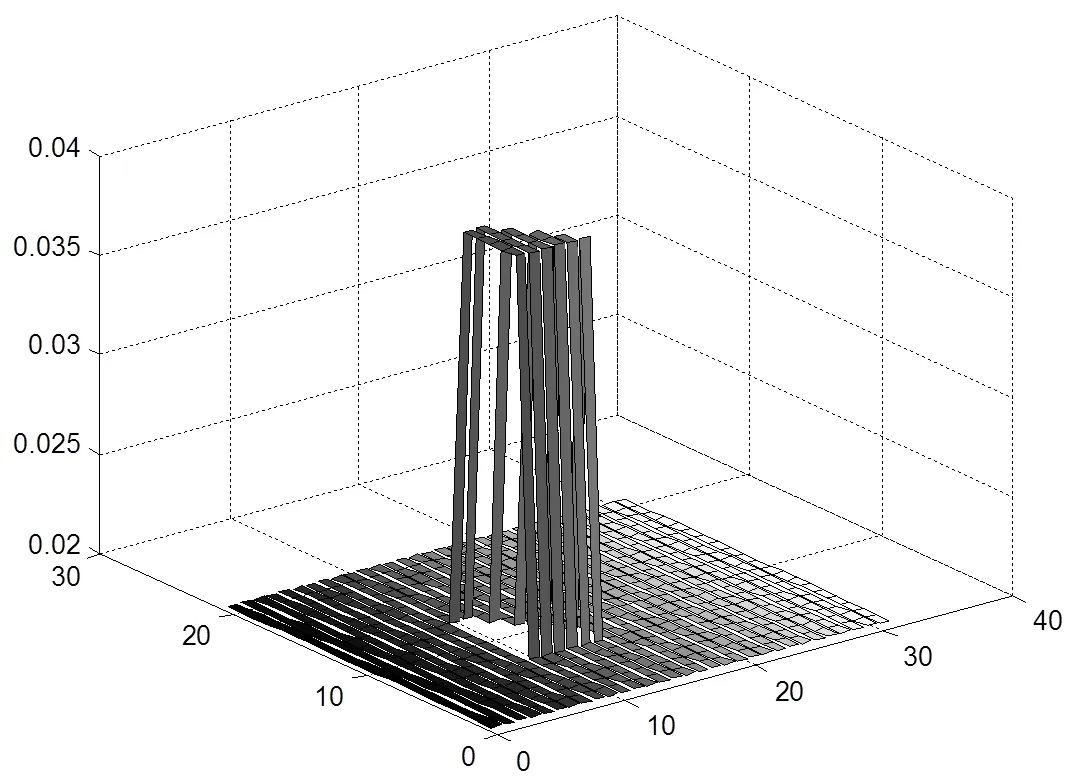
图1 电导率模型
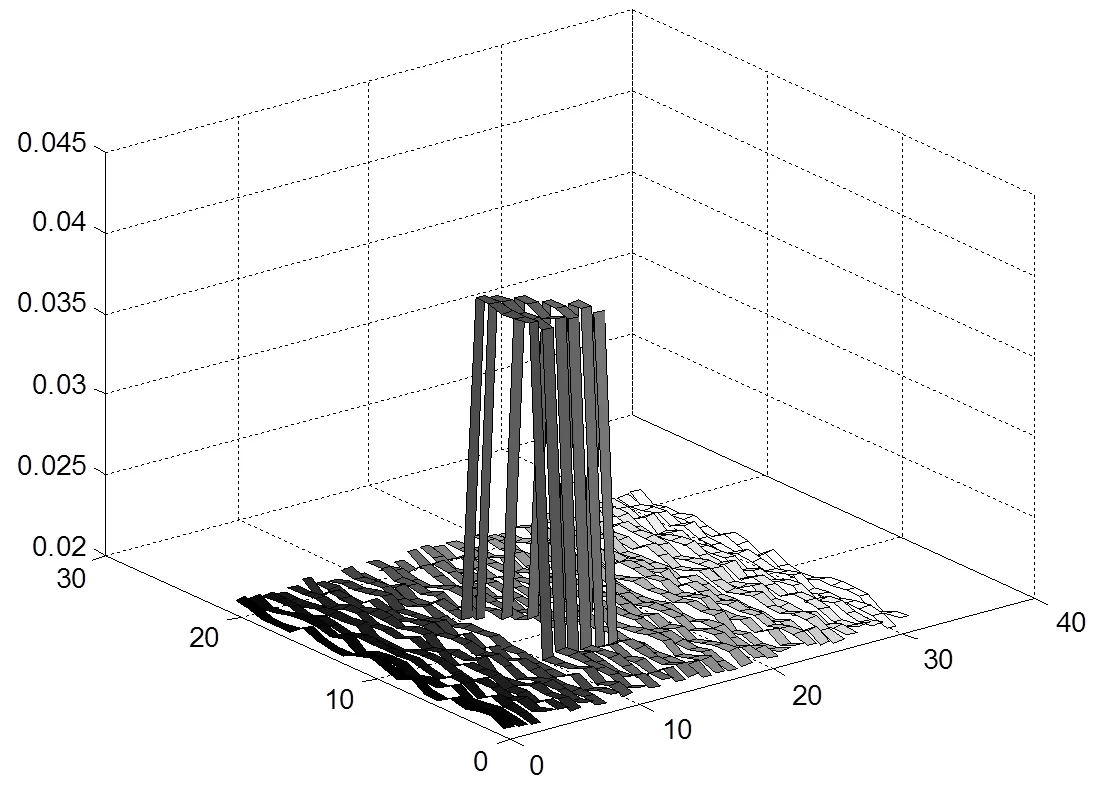
图2 共轭斜量法对电导率的识别结果
根据电导率的识别结果与电导率模型对应的真值之间的绝对误差为0.0087和相对误差为0.013,可见大范围收敛共轭斜量法可以有效地应用于麦克斯韦方程反演问题.
4 结语
为了有效克服麦克斯韦方程反演过程中所固有的非线性以及不适定性等困难,本文提出的一种综合共轭斜量法和同伦反演法优点的大范围收敛的共轭斜量反演方法,解决了求解过程中局部陷入极小值的困惑. 在其他类型的参数识别问题也可以应用本文的方法.
[1] 李 壮, 韩 波. Maxwell方程反问题的小波-微分正则化算法[J]. 黑龙江大学自然科学学报, 2007, 24(6): 708-711.
[2] 张新明, 刘家琦, 刘克安. 一维双相介质孔隙率的小波多尺度反演[J]. 物理学报, 2008, 57(2): 601-620.
[3] ZHAI SHUANGZHU, CHEN YONG, HAN BO, et al. A strategy for the parameter inversion of two-dimensional elastic wave equation based on total variation regularization method[J]. Advanced Science Letters, 2012, 11(1): 274-280.
[4] 丁 亮, 韩 波, 刘润泽, 等. 基于探地雷达的混凝土无损检测反演成像方法[J]. 地球物理学报, 2012, 55(1): 317-326.
[5] 李 壮, 韩 波, 陈 勇. 探地雷达反问题的小波-同伦混合反演算法[J]. 计算物理, 2009, 26(1): 87-93.
A Widely Convergent Conjugate Gradient Method for Maxwell Equation Inversion
WANG Ying
(Department of Mechanical Engineering, Heilongjiang Industrial College, Jixi158100, China)
For the problem of conductivity parameter inversion in the Maxwell equation, It constructs a regularization-conjugate gradient inversion algorithmwith a widely convergence. The widely convergentnumerical algorithm which can solve the inversion problem of Maxwell equation is gained by organically combining the Homotopy method with global convergence for solving the nonlinear problems, and the conjugate gradient algorithm for solving the large-scale optimization problems with the regularization method Tikhonov for solving the ill-posed problems. The constructed algorithm is used to solve the inverse problem of conductivity parameter and solves the puzzle that the solution falls into the local minimal value in the solving process. The experimental result shows that the algorithm is effective, and can be applied in the parameter identification problems of other types.
Maxwell equation; Inversion; Homotopy method; Conjugate gradient algorithm
O241.82
A
2095-4476(2014)05-0005-04
2014-04-28;
2014-05-10
王迎(1984— ), 女, 黑龙江牡丹江人, 黑龙江工业学院机械工程系助教
(责任编辑:饶 超)

