高耸闪蒸塔调谐质量阻尼减振技术的数值分析*
胡 朋,何立东,郝 伟,王 锎
(北京化工大学化工安全教育部工程研究中心,北京100029)
0 引 言
在石化企业中,有许多种高耸石化设备,例如分馏塔、蒸馏塔、化工烟囱等。它们是一种高度与直径之比较大的构筑物,柔性较大且固有频率较低。在各类荷载中,风荷载对高耸结构是最重要的,不仅结构应力的80%~90%是风荷载引起的,高耸结构振动控制的动力源也是风荷载[1]。因高耸石化设备长径比较大,结构抗弯刚度相对较柔,在强风作用下会产生较大的振动和变形,给运行安全带来隐患,且容易造成设备疲劳损伤,缩短使用寿命等[2-3]。因而,设置结构振动控制装置来主动减小风振响应显得尤为必要。
对于高耸石化设备,若采用增大截面提高刚度的传统抗风设计方法,设备的直径和壁厚就要增大很多,势必大大增加工程造价,非常不经济,还有可能加剧结构的动力反应[4];若加焊破风圈,焊接后会产生应力集中,而应力释放后又有向内凹的可能[5],会对石化设备造成一定程度的损坏;若加装框架支撑体系,当结构较高时,其刚度往往不够,且节点设计和施工都很复杂,会使主体结构含钢量增加,不够经济合理[6];若装配拉索,在强风激励下,拉索的强振动将导致疲劳破坏与连接损坏,从而丧失对结构的支撑作用,危及结构的安全[7]。
相比之下,调谐质量阻尼器(TMD)因其结构紧凑、安装方便、维护费用低、控制效果稳定、效率高而广泛应用于各种结构的振动控制,尤其适用于高耸结构的风振控制[8-9]。但就国内来讲,其应用领域主要集中在电视塔、高楼、输电塔、桥梁等结构上,在高耸石化设备上的应用很少。因而,如何将TMD减振技术有效地移植到石化领域里值得深入研究。
本研究以湖南岳阳某石化企业的高耸闪蒸塔为例(实物图如图1所示),针对其风振响应过大的问题,采用Matlab数值模拟的方式,研究TMD参数对该设备风振控制效果的影响,并寻求TMD的最优匹配参数以达到最佳的减振效果,为TMD的实际工程应用提供技术参考。

图1 高耸闪蒸塔
1 顺风向脉动风荷载的数值模拟
自然界的风包括平均风和脉动风两种成分。在进行结构分析时,通常将周期较长的平均风视为静力,而将周期较短、随机性较强的脉动风视为动力。高耸结构的风振响应主要就是脉动风引起的。脉动风实际上是三维的风湍流,但由于垂直向与横风向的湍流较小,一般只讨论顺风向湍流。因此,本研究按照相关建筑结构规范的要求,采用模拟精度较高、数学基础严密的谐波叠加法并依据Davenport风速功率谱[10]来对顺风向脉动风荷载进行数值模拟,其表达式如下:
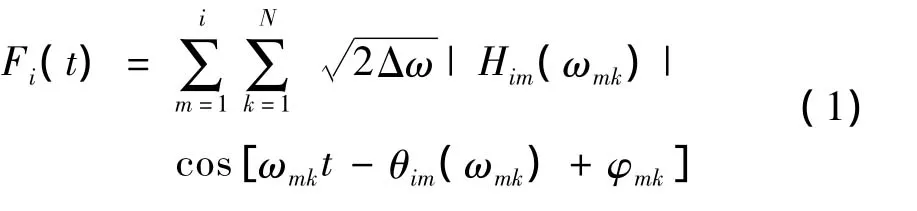
式中:Fi(t)—第i个集中质量处的顺风向脉动风荷载;Δω—频谱分度,Δω =ωu/N,其中:N—频谱样本点;ωu—脉动风荷载的截止圆频率;Him(ωmk)—脉动风荷载的功率谱密度函数矩阵进行Cholesky分解后所得下三角矩阵的第(i,m)个元素,其中ωmk=(k-1+m/n)Δω,n表示脉动风荷载的模拟维数;θim(ωmk)—竖向高度两个不同集中质量间的相位角,θim(ωmk)=arctan[lm(Him(ωmk))/Re(Him(ωmk))];φmk—满足均匀分布的随机数,介于0~2π之间。
本研究所描述的方法并依据Davenport风速谱在频率截取区间[0,ωu]所包含的能量来进行截止圆频率ωu的合理选择[11]。ωu分别取不同数值时,截取区间能量与总能量的比值如表1所示。由表1中数据可知,当截止频率取6π时,比值已经达到96.31%,并考虑到数值模拟会消耗大量机时,本研究确定截止频率ωu取6π,即3 Hz。

表1 截取区间能量与总能量的比值
当进行脉动风荷载的数值模拟时,需要对时间t进行离散,根据采样定理,采样频率必须大于信号最高频率的两倍,具体到本研究中即是采样时间间隔Δt≤π/ωu=0.17 s,故本研究取 Δt=0.01 s。
根据以上对顺风向脉动风荷载的阐述,笔者采用Matlab数学软件对其进行了10 min的数值模拟,得到了较好的随机风荷载样本。
2 高耸闪蒸塔的风致振动
2.1 闪蒸塔的简化
对于高耸塔架结构,一般建立二维串联多自由度模型就足以满足动力计算和减振分析的要求。由于高耸闪蒸塔内部构造简单且壁厚除个别地方外皆相同,本研究将其简化为内径1 400 mm、壁厚14 mm、高30 000 mm的等截面匀质悬臂梁并离散为10个自由度的二维竖向串联集中质量多自由度体系,高耸闪蒸塔及其简化模型如图2所示。
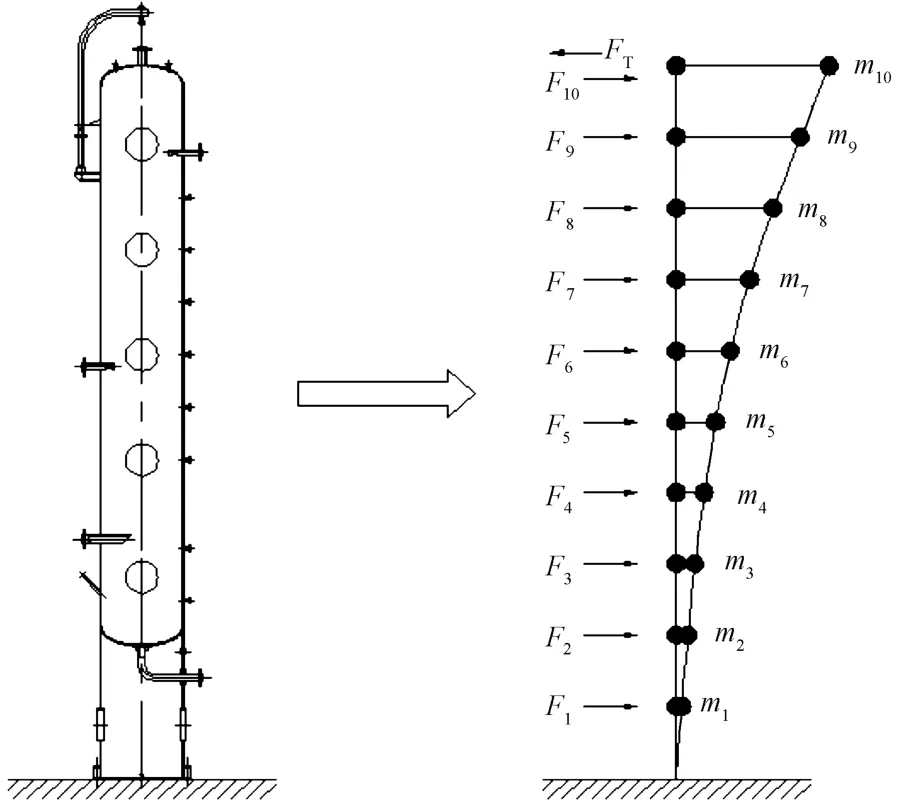
图2 高耸闪蒸塔及其简化模型
本研究利用集中质量法获得了简化模型的质量矩阵M,又采用悬臂梁挠曲线方程获得了简化模型的柔度矩阵,求逆运算后得到刚度矩阵。由于挠曲线方程并没有考虑剪切变形的影响,将刚度矩阵乘以折减系数0.9得到实际刚度矩阵K。为了验证所得M与K的正确性,本研究对简化模型进行了模态分析并与ANSYS三维模型所得结果进行了对比(对比情况如表2所示),可知本研究所采用的简化模型是正确的。高耸结构的阻尼矩阵C一般假定为瑞利阻尼,可由M与K计算得到。

表2 模态分析结果比较
2.2 闪蒸塔的风振
本研究采用Newmark数值积分法并将模拟生成的10条脉动风荷载时程曲线代入式(2),便可求得简化模型的风振响应。
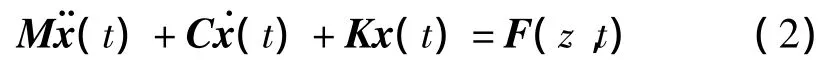
式中:M,C,K—简化模型的质量矩阵、阻尼矩阵与刚度矩阵(t),(t),x(t)—简化模型相对于地面的加速度、速度与位移列阵;F(z,t)—作用于简化模型各个集中质量上的脉动风荷载列阵。
3 TMD的风振控制
3.1 风振控制方程
由表1可知,脉动风荷载的能量主要集中在0~1 Hz的频域区间内,且本研究设定的截止频率为3 Hz,又由表2可知,简化模型的一阶频率为1.48 Hz而二阶频率为9.18 Hz,因此可以说明,在顺风向脉动风荷载的作用下,高耸闪蒸塔的风振响应主要是第一振型的贡献,其他高阶振型的贡献较小。于是,减小风振响应就主要考虑对第一振型的控制而将TMD安装在设备顶部,TMD减振模型如图3所示。
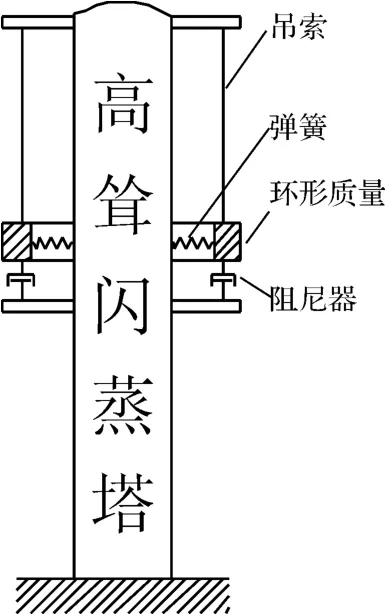
图3 TMD减振模型
该TMD主要由吊索、弹簧、环形质量以及阻尼器组成。当脉动风荷载激励时,环形质量与闪蒸塔产生相对运动,此时环形质量产生的控制力将作用在闪蒸塔上,当其摆动频率与闪蒸塔的一阶固有频率接近时引起共振,环形质量则吸收闪蒸塔的部分能量以减少其风振响应,吸收的能量再由与环形质量连接的阻尼器耗散掉,从而达到对结构施控的目的。
利用TMD进行高耸闪蒸塔风振控制的相关方程如下:
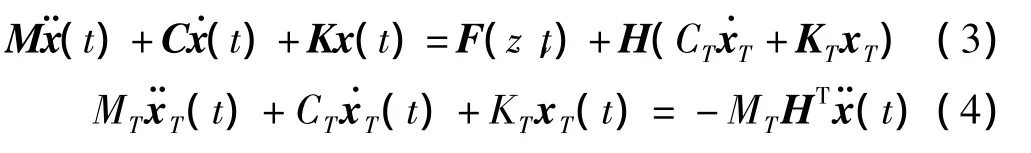
式中:MT,CT,KT—TMD的环形质量、等效阻尼与等效刚度;¨xT(t),˙xT(t),xT(t)—TMD相对于闪蒸塔的加速度、速度与位移;H—TMD的作用位置向量,H=[0 0 0 0 0 0 0 0 0 1]T。
为了能够从本质上反映TMD的风振控制效果,此处引入3个参数,即质量比μ、频率比f与TMD自身的阻尼比ζ,其具体表达式如下:
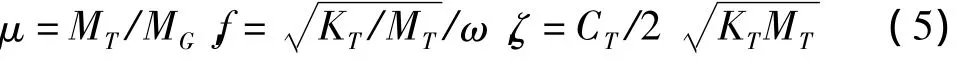
式中:MG—闪蒸塔的质量;ω—闪蒸塔的一阶圆频率。
考虑到高耸闪蒸塔的承重能力等客观限制条件,本研究选定质量比μ为0.01、0.02与0.03来进行数值计算,且阻尼比ζ与频率比f的计算步长为0.01。
3.2 风振控制效果
本研究对不同质量比下的频率比与阻尼比进行了寻优以达到最佳的减振效果,并给出了TMD最大相对位移,具体如表3所示。
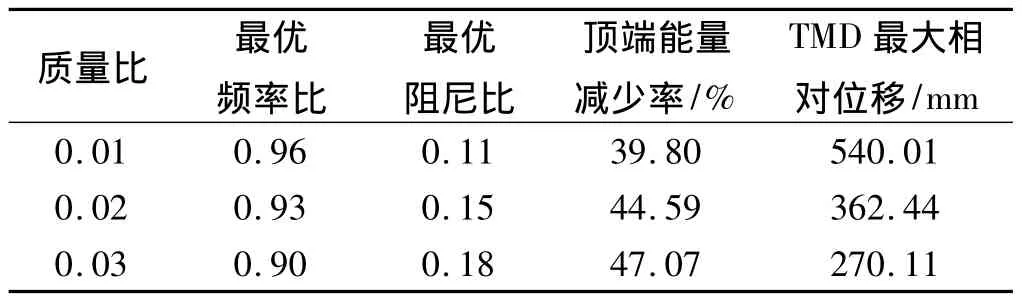
表3 不同质量比下的最优参数
对于不同质量比下的最优参数,本研究计算了各集中质量处的位移响应最大值,计算结果如表4所示。综合表3与表4可以看出,当TMD取质量比0.03所对应的最优匹配参数时,顶端能量减少率、TMD最大相对位移、各集中质量处的位移响应最大值都是最佳的,而且此时的顶端位移最大值并未超出《高耸结构设计规范》所限定的范围。故本研究所得到的最优匹配参数为:质量比0.03、频率比0.90、阻尼比0.18。
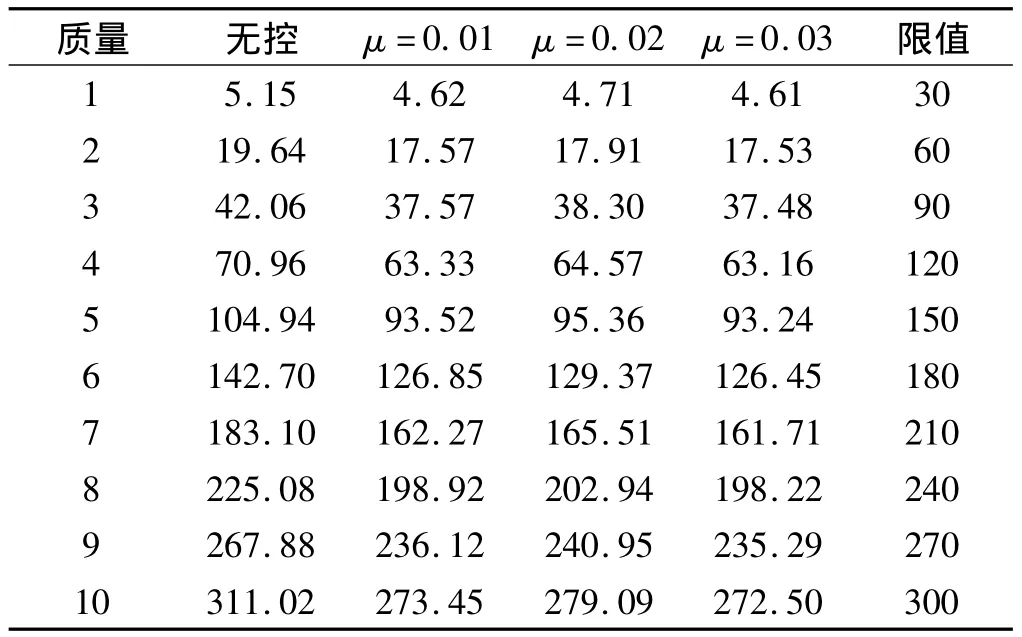
表4 各集中质量处的位移响应最大值(单位:mm)
有、无TMD时高耸闪蒸塔顶端的位移时程曲线如图4、图5所示,可以看出响应幅值得到了有效控制。TMD对高耸闪蒸塔的风致振动具有很好的控制效果,但偶尔也会有较大的位移响应(尽管并未超过限值)。
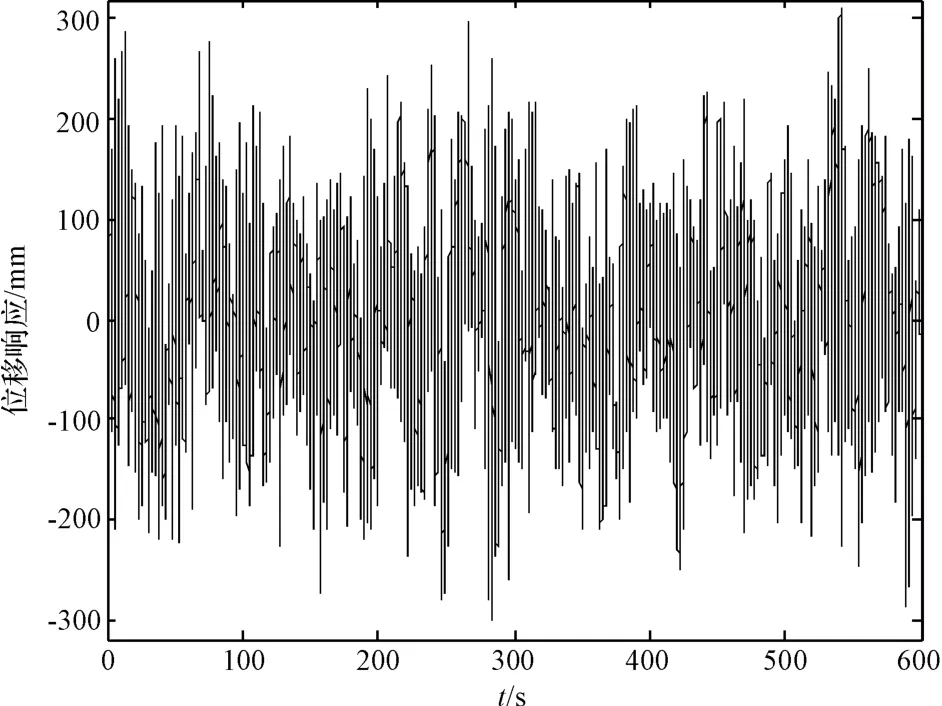
图4 无控时顶端位移响应
考虑到一般情况下安装与运行TMD的实际空间有限,故在TMD的设计中存在一个不容忽视的问题,即TMD相对于闪蒸塔的最大运行位移。因而,为了适应有限的空间,可能需要适当调整TMD的最优匹配参数。本研究给出了质量比为0.03的工况下,闪蒸塔顶端能量减少率(能量减少率的等值线图如图6所示),可以通过协调二者的关系来解决空间有限的难题。
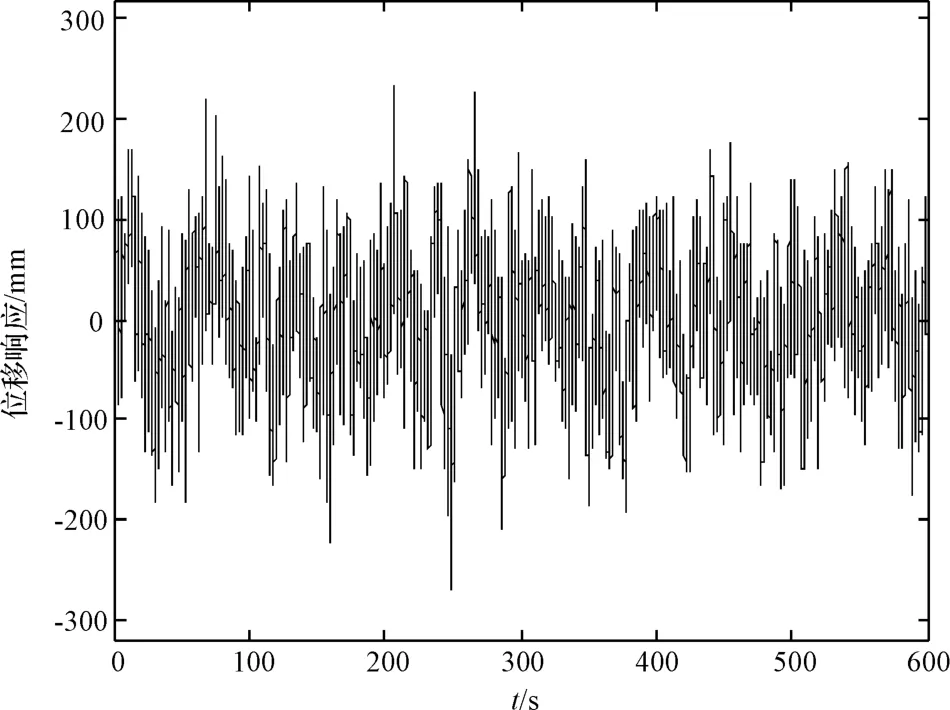
图5 有控时顶端位移响应

图6 能量减少率的等值线图(%)
4 结束语
(1)通过对高耸闪蒸塔设置TMD阻尼控制装置能够主动减小风振响应。通过模态分析可知,高耸闪蒸塔的风振响应主要以第一振型为主,其他高阶振型的贡献较小。因而,减小风致振动时主要考虑对闪蒸塔第一振型的控制,故将TMD安装在设备顶部,并调谐至一阶频率附近。
(2)通过参数寻优,本研究获得了TMD的最优匹配参数,即质量比0.03、频率比0.90、阻尼比0.18。在该最优匹配参数下,高耸闪蒸塔顶端风振能量减少了47.07%,顶端最大位移减少了约40 mm,并未超出《高耸结构设计规范》所限定的范围,而且各集中质量处的最大位移响应都有不同程度的减少。
(3)考虑到TMD安装与运行的实际空间有限,本研究给出了闪蒸塔顶端振动能量减少率与TMD最大相对位移的等值线图,可以通过协调二者的关系来解决空间有限的难题。
[1]王肇民.高耸结构振动控制[M].上海:同济大学出版社,1997.
[2]冯 甦,金 江.高耸钢塔结构的脉动风荷载模拟及结构风振响应分析[J].南通大学学报:自然科学版,2007,6(1):67-71.
[3]朱晓辉.MR阻尼器用于电视塔结构风振控制的研究[D].湖北:武汉理工大学土木工程与建筑学院,2004.
[4]呼学军,葛建平.某高耸结构TMD风振控制研究[J].山西建筑,2007,33(32):81-82.
[5]何建宇,赵文波,王 建.浮顶罐密封不严的原因分析[J].硅谷时代,2009(11):4.
[6]罗 仁.多高层建筑钢结构抗侧力体系综述[J].钢结构,2001,16(3):47-50.
[7]金 林,应祖光,罗银淼.斜拉索的不稳定振动及控制[J].噪声与振动控制,2004,24(5):5-7.
[8]秦 丽,闫维明,呼学军,等.河南艺术中心标志塔TMD地震控制[J].北京工业大学学报,2009,35(6):761-768.
[9]向 敢,翁泽宇,王 辉,等.基础柔性对深筏隔振系统振动特性的影响[J].轻工机械,2013,31(5):30-33.
[10]DAVENPORT A G.The spectrum of horizontal gustiness near the ground in high winds[J].Quarterly Journal of the Royal Meteorological Society,1962,88(376):197-198.
[11]白 泉,朱浮声,康玉梅.风速时程数值模拟研究[J].辽宁科技学院学报,2006,8(1):1-3.

